Adaptive accurate tracking control of HFVs in the presence of dead-zone and hysteresis input nonlinearities

Zehong DONG, Yinghui LI, Maolong LV, Renwei ZUO

a Graduate College, Air Force Engineering University, Xi’an 710100, China

b Aeronautics Engineering College, Air Force Engineering University, Xi’an 710038, China

c Delft Center for Systems and Control, Delft University of Technology, Mekelweg 2, Delft 2628 CD, The Netherlands

KEYWORDS Accurate tracking control;Back-stepping control;Dead-Zone and hysteresis;Hypersonic flight vehicles;Non-affine model

Abstract A novel accurate tracking controller is developed for the longitudinal dynamics of Hypersonic Flight Vehicles (HFVs) in the presence of large model uncertainties, external disturbances and actuator nonlinearities. Distinct from the state-of-the-art, besides being continuity,no restrictive conditions have been imposed on the HFVs dynamics. The system uncertainties are skillfully handled by being seen as bounded ‘‘disturbance terms”. In addition, by means of backstepping adaptive technique, the accurate tracking (i.e. tracking errors converge to zero as time approaches infinity) rather than bounded tracking (i.e. tracking errors converge to residual sets)has been achieved. What’s more, the accurate tracking problems for HFVs subject to actuator dead-zone and hysteresis are discussed,respectively.Then,all signals of closed-loop system are verified to be Semi-Global Uniformly Ultimate Boundness (SGUUB). Finally, the efficacy and superiority of the developed control strategy are confirmed by simulation results.

1. Introduction

Hypersonic Flight Vehicles (HFVs) have attracted more and more attention recently on account of the high speed and high cost performance,processing great military and civilian values.In recent years, tremendous efforts including model investigation and controller design in Refs.1-15have been made. It is worth noting that there exist strong uncertainties in HFVs dynamics due to the strong dynamics coupling, fast timevarying flight environment and unknown actuator nonlinearities.5,10In addition, the integration of the propulsion system and the body enhances the dynamics coupling characteristics and nonlinearities, making the controller design for HFVs more complicated.13

In order to deal with the large system uncertainties in HFVs dynamics, numerous control methodologies have been proposed, including robust control,5,6sliding mode control,8-10intelligent control,11,12prescribed performance control,13-15etc. These literatures have made great contributions to HFVs research. From a practical perspective, a key issue that may be often encountered is that the control inputs cannot be implemented accurately because of actuator input nonlinearity.16However, the aforementioned works did not take into full consideration the actuator input nonlinearities such as dead-zone and backlash due to the existence of hydraulic actuator and hinge.In practice,the existence of actuator nonlinearity not only degrades the control accuracy and the flight performance, but even causes system instability in severe case.17With the development of HFVs control technique, the issues of actuator input nonlinearity are getting more and more attention in controller design. To list a few, an adaptive fault-tolerant control strategy is addressed to deal with the issue of input saturation and actuator fault in Ref.18Nevertheless, the dead-zone and hysteresis nonlinearities are not addressed therein. In Ref.19a neuro-adaptive approach is presented to cope with the problem of unknown actuator deadzone for switched stochastic nonlinear systems, where the uncertainties of system are estimated by radial basis function neural networks(RBFNNs).An observer-based adaptive controller is address to eliminate the unfavorable effect caused by actuator dead-zone and hysteresis in Ref.20where the unknown dynamics are approximated via fuzzy logic systems.21In Ref.22RBFNNs are introduced to estimate the dynamic uncertainties caused by the input constraints and external disturbances.What’s more,an improved performance function is proposed so as to guarantee some predefined transient and steady state attributes in the presence of dead-zone in Ref.23

Unfortunately, to our best knowledge, the abovementioned literatures are merely able to achieve bounded tracking, i.e., tracking errors converge to a residual set whose size relies on some unknown design parameters. In other words,accurate tracking control for HFVs has not been investigated in state-of-the-art. Noting that accurate tracking for HFVs is of paramount importance in practice, such as large maneuver flight,24precision strike,25and so on.More recently,some accurate tracking control methodologies are proposed for nonlinear systems.26-28In Ref.26a novel adaptive filter for the nonlinear hysteretic system is addressed to implement the accurate tracking for reference trajectory. Furthermore,Ref.27exploits an adaptive asymptotic control scheme for pure-feedback system, in which the form of model is transformed from non-affine to affine by defining a novel function.Nevertheless, owing to the existence of unmodeled dynamics,fast time-varying flight environment and external disturbances of HFVs, these accurate tracking control methods cannot be applied directly to the HFVs, especially when the unknown dead-zone and hysteresis nonlinearities appear.16,23Therefore,how to design an accurate tracking controller for HFVs in the presence of dead-zone and hysteresis nonlinearities needs to be clearly exploited.

In recent years,Back-Stepping Control(BSC),which is perceived as a direct effective mean to design the controllers for nonlinear systems,29-31is generally applied for implementing tracking control for HFVs.32Motivated by above observations, this work develops a back-stepping adaptive accurate tracking control for HFVs in spite of actuator dead-zone and hysteresis nonlinearities. The main contributions of this article are as follows:

(1) To the best of authors’ knowledge, this might be a pioneering work achieving accurate tracking for HFVs subject to uncertain dead-zone and hysteresis nonlinearities. Compared with most of available researches on HFVs in Refs.6,7and Refs.13-17the velocity and altitude tracking errors can accurately converge to zero rather than a residual set.

(2) In contrast to the conventional adaptive neural control in Refs.7,13,33the neural networks are removed and only one parameter needs to be updated in each control law.Thus, the proposed method is simpler and can reduce the computational burden in theory.

(3) In comparison with Ref.23and Refs.34,35, a novel zeroerrors tracking control scheme for HFVs is further presented against the system uncertainties caused by actuator nonlinearity and external disturbance, where the system uncertainties are skillfully disposed by being regarded as bounded ‘‘disturbance terms”.

The remainder of this paper is organized as follows.In Section 2, model description and preliminaries are provided.Then, the controller design process is given in Section 3 and the close-loop stability is analyzed in Section 4. In Section 5,simulation results are presented to prove the effectiveness of the proposed scheme and the conclusions are included in Section 6.

2. Model description and preliminaries

2.1. Longitudinal dynamics of HFVs

The longitudinal dynamic model of HFVs is considered as36

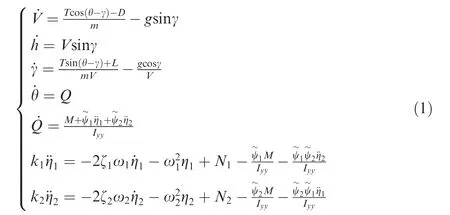
where T, D, L, M, N1and N2can be formulated as

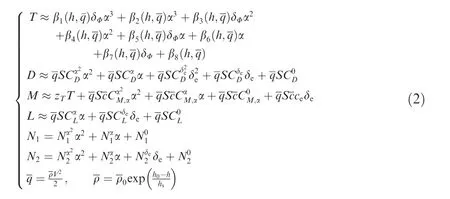
where the more detailed definitions can be consulted in Refs.36,37

2.2. Actuator nonlinearities

During the flight, the actuators of HFVs may present uncertain nonlinearities, which significantly increase the difficulty of controller design and threaten the flight safety.The actuator model is considered as ϑ = υ(u ) where u and ϑ denotes the input and output of actuator, respectively, υ(·) is an unknown nonlinear function. In this work, two negative characteristics of actuator, dead-zone and hysteresis, are taken into accountant.

The dead-zone model is described as follow38

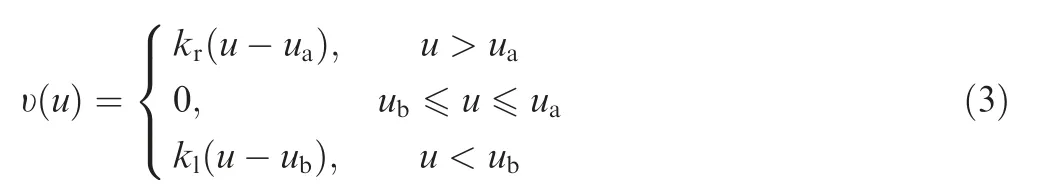
where uaand ubdenote breakpoints of the dead-zone model,kland krrepresent left and right slope of dead-zone nonlinearity.The hysteresis characteristic is described by the Bouc-Wen model as26

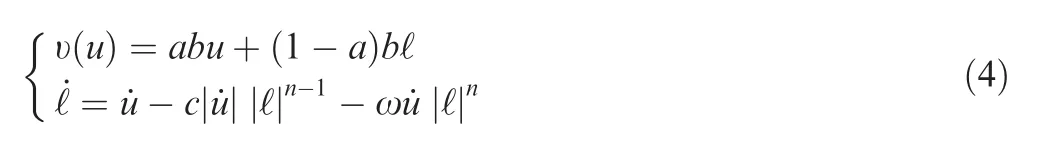
where c and ω are constants depicting the shape and amplitude of the hysteresis and the readers can refer to Ref.26for more details. The curves of the Eqs. (3) and (4) are depicted in Fig. 1, where the parameters are set as kr=kl=10/9,ua=0.1, ub=-0.1, a=1/3, b=3, c=1, ω=0.5, ℓ(0 )=0,u(t )=4sin(2t ).

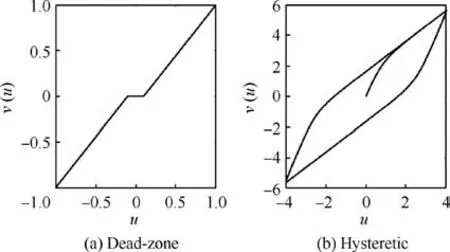
Fig 1 Dead-zone and hysteresis characteristics.

Remark 1.In fact,it is worth noting that actuator nonlinearities as dead zone and hysteresis exist in a wide range of HFVs due to the electronic circuits, hydraulic servo values and mechanical connections.23To make matters worse, the dead zone and hysteresis nonlinearities may induce deterioration of the system performance even lead to instability of the closed-loop system.39Thus,it is extremely meaningful to exploit the control for HFVs in the case of dead zone and hysteresis nonlinearities.

2.3. Model transformation and decomposition

It can be seen from Eqs.(1)and(2)that V is mainly related to Φ and h is mainly governed by δe,respectively.13Thus,in order to simplify the controller design, the HFVs dynamics are decomposed into velocity subsystem and altitude subsystem in this work. Inspired by Refs.13,40the velocity subsystem is considered as

Remark 2.During the flight, the aerodynamic parameters will change with the variation of flight environment, the functions fVand gVare affected by the aerodynamic parameters. Indeed, an exact model for HFVs is difficult to be obtained since the complex flight environment of HFVs is hard to be reproduced in a wind tunnel.6In order to increase the robustness of system,we regard fVand gVas unknown functions.

On account of the fact that γ is fairly small during cruise phase, so the approximations sinγ ≈γ and cosγ ≈1 stand,41then the velocity subsystem can be formulated as

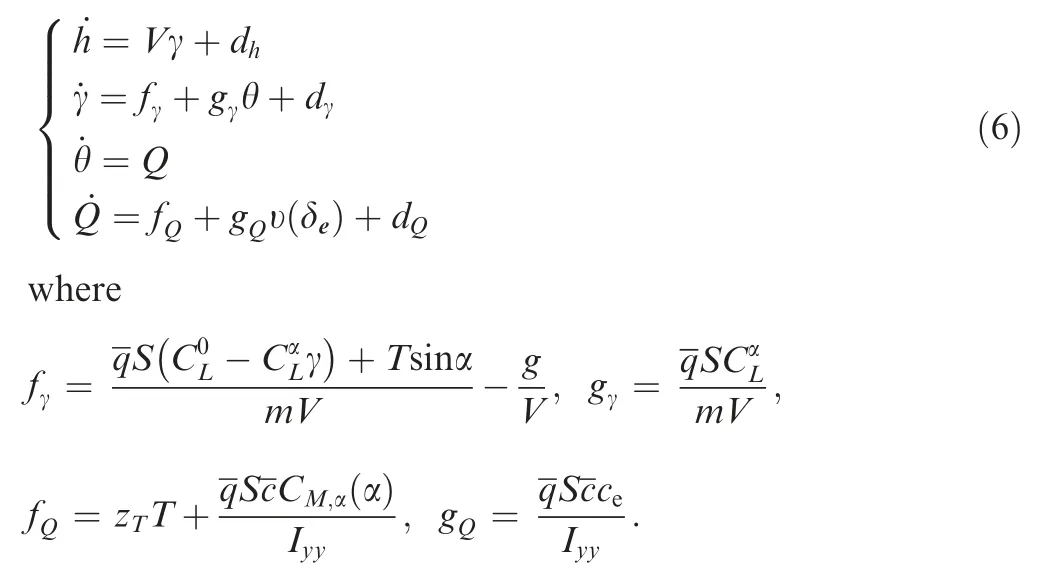
Similarly to velocity subsystem, the functions fγ, gγ, fQand gQare unknown and υ(δe) represents the uncertain nonlinearity of δe.dh,dγ,dθand dQare the lumped perturbations on altitude, flight path angle and pitch rate resulting from aerodynamic coefficients uncertainties and external disturbances, respectively.

Assumption 1.37The sign of g*is assumed to be known.Further,there exist positive functions f*M, g*mand g*Msuch that|f*|≤f*Mand g*m≤|g*|≤g*Mwhere m represents minimum of

* and M represents maximum of *; * denotes V,γ and Q,respectively.

Assumption 4.16In view of Eqs.(5)and(6),the input of actuator implicitly appears in HFVs dynamics and there exists a nonlinear relationship between the input and the output of actuator in presence of dead-zone and hysteresis nonlinearities. Taking notice of Fig. 1, we assume that υ(u ) satisfies υmu+lm≤υ(u )≤υM+lMand there exist positive constants υm,υM,lmand lMsuch that υm≤υ ≤υMand lm≤|l|≤lM.From the inequation υmu+lm≤υ(u )≤υM+lM, it can be deduced by mean value theorem that

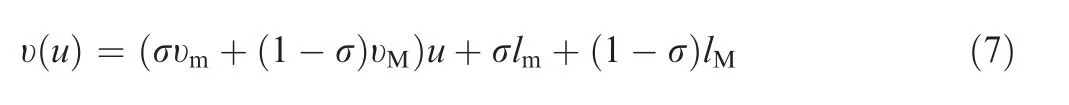
where σ is a positive function satisfying 0 ≤σ ≤1. From Eq.(7), υ(u ) can be further written in the following form

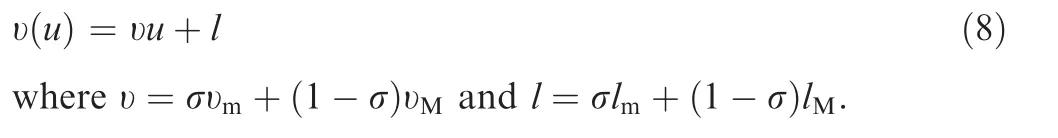
Remark 3.In the control design of HFVs, input dead-zone and hysteresis are widespread problems that need to be solved urgently due to the wide existence of hydraulic actuator and hinge in HFVs.23,35It is noting that dead-zone and hysteresis input nonlinearities are non-smooth and the control input appears in the system function as a non-affine form, which makes the controller design quite complex. From Fig. 1, we can see that there exists that υmu+lm≤υ(u )≤vM+lMwith respect to dead-zone and hysteresis nonlinearities.Consequently,the dead-zone and hysteresis nonlinearities are transformed into affine form as Eq. (8). In the later controller design, the nonaffine forms of input nonlinearity are treated as a linear function by Eq. (8), where υ and l are bounded.

Lemma 142. For any positive constants κ and ι, the following inequality holds

The control objection is that V and h can accurately track their own reference trajectories via the proposed adaptive control for HFVs in the presence of the dead-zone and hysteresis input nonlinearities.

3. Adaptive accurate tracking control

3.1. Velocity controller design

The velocity tracking error is defined as

The derivate of eVis

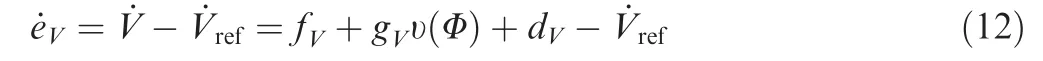
Define the Lyapunov function candidate:

Noting Eqs.(8),(12)and(13),we can obtain the derivative of LeVas

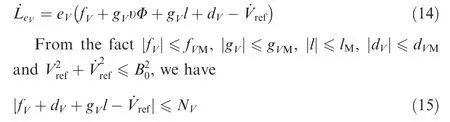
where NV=fVM+gVMlM+dVM+B0is a unknown bounded positive constant. Besides, we take ^NVas the estimate of NVand define= NV- ^NV.

Construct the actual control law as Eq. (16), the adaptive law is chosen as Eq. (17)

Consider the following Lyapunov function candidate

From Eqs. (14)-(17), the derivate of LVis given as

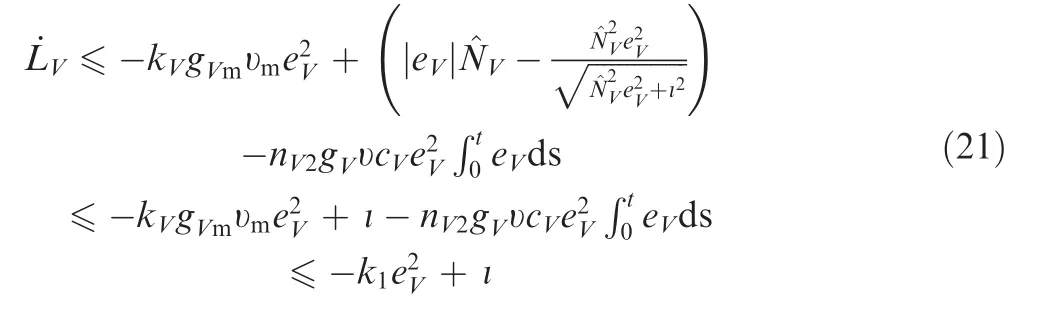
where k1=kVgVmυm.

3.2. Altitude controller design

In this section, the adaptive accurate tracking controllers are developed based on BSC for Eq. (6). The virtual control law χ, the actual control law δeand the adaptive law ^N are designed to make the tracking error e accurately converges to zero. The tracking errors of altitude subsystem are defined as following

The derivate of ehcan be written as

Consider the following Lyapunov function candidate

Then the derivate of LeVcan be obtained as

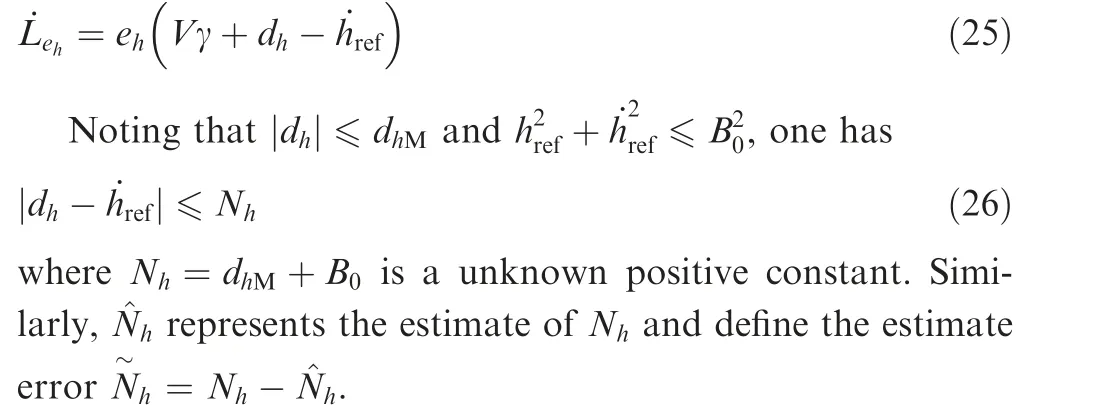
Construct the virtual control law and the adaptive law as

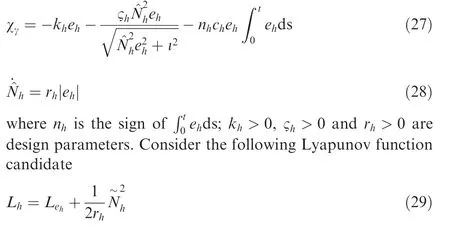
Substituting Eqs. (25)-(28) into Eq. (29), then the derivate of Lhis provided as

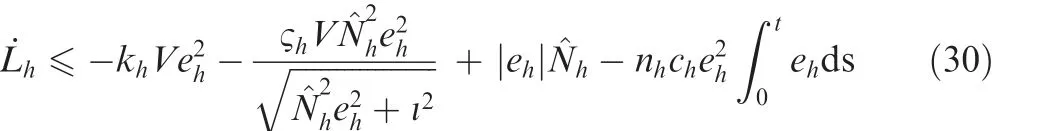
Choosing ςh≥V-1and utilizing Lemma 1, one has

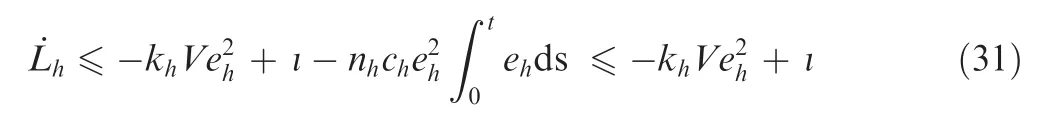
Similarly, we construct the virtual laws as

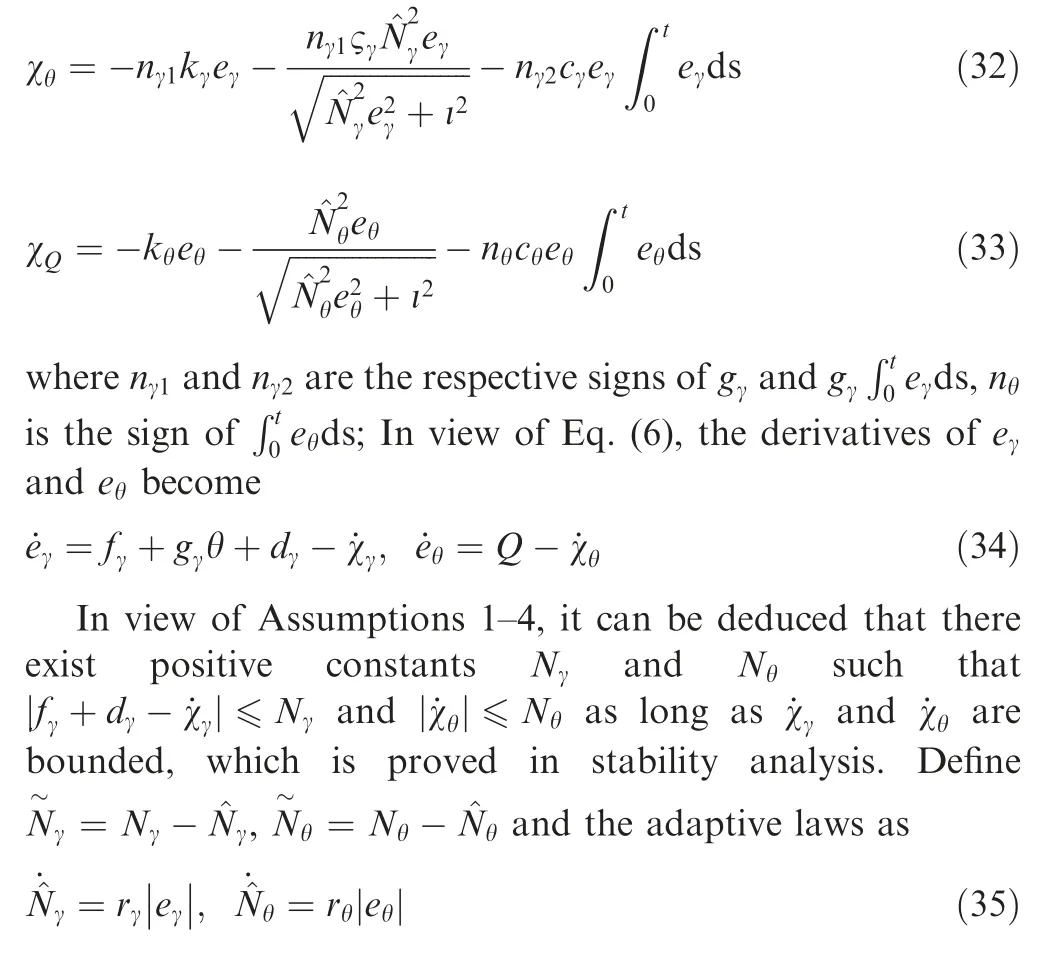
Define the following Lyapunov function candidate

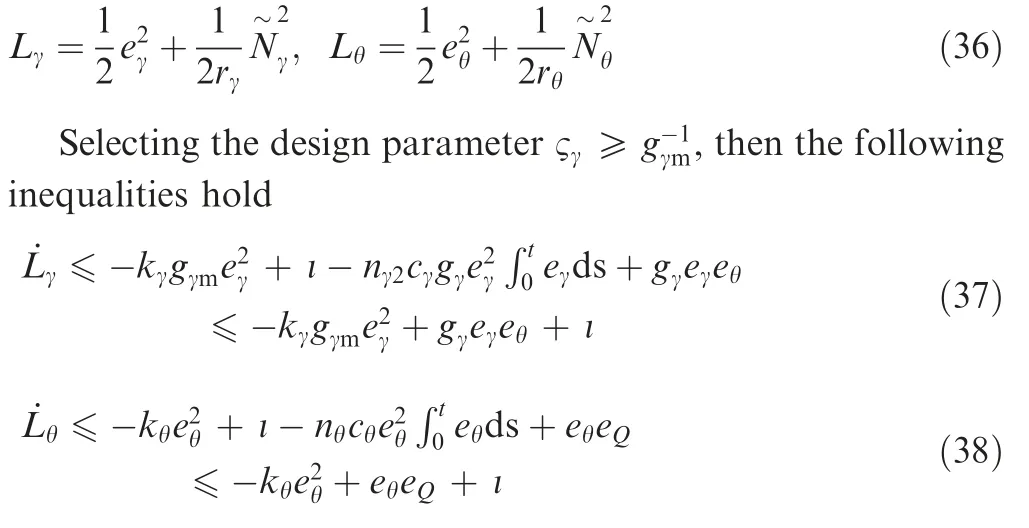
In view of Assumption 1 and with the help of Young’s inequation, we have

In the altitude controller design, the uncertain nonlinearity of actuator is considered,according to Eq.(22),the derivate of eQleads to

Consider the Lyapunov function candidate

Substituting Eqs. (43)-(45) into Eq. (46), we obtain

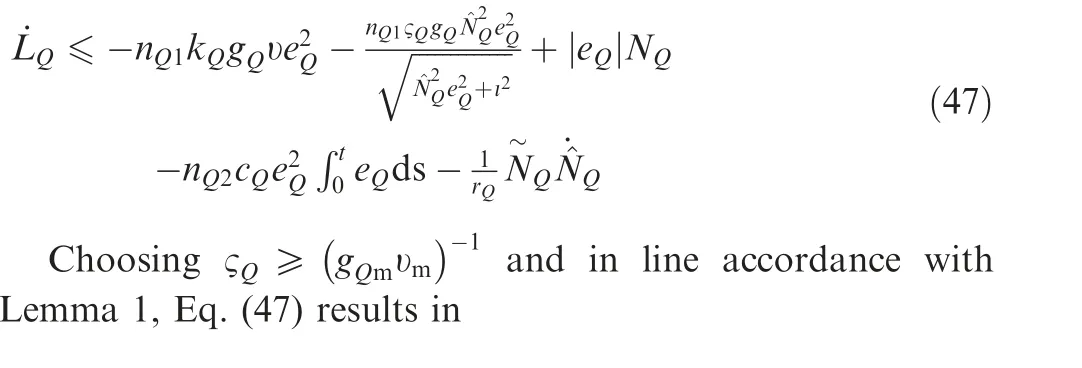
Fig 2 Block diagram of adaptive accurate tracking for HFVs with the actuators dead-zone or hysteresis.

The aforementioned design procedure of the accurate tracking controllers for HFVs can be depicted by a block diagram as shown in Fig. 2.

4. Stability analysis

where p is a positive constant and the tracking errors eVand ehcan accurately converge to zero.

Proof. Construct the Lyapunov function candidate

It follows Eqs. (29), (31), (36)-(40), (46) and (48) that the derivate of L can be expressed as

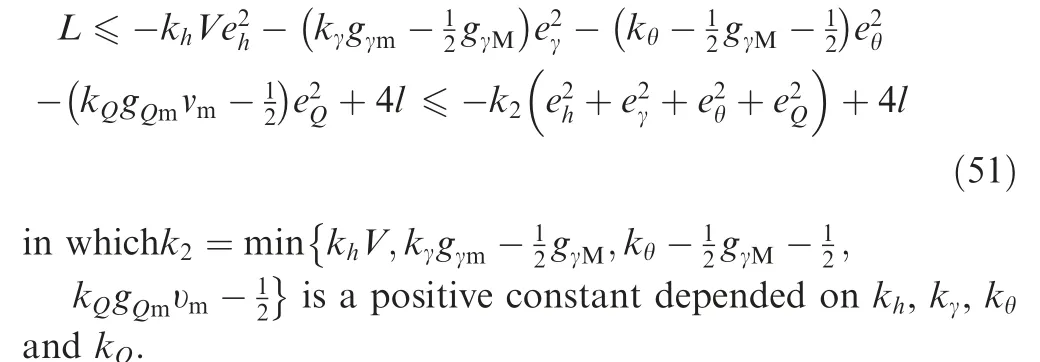
Integrating both sides of Eqs. (21) and (51), yields

It follows Lemma 2 that

Accordingly, the accurate adaptive tracking control for HFVs in the presence of the dead-zone and hysteresis input nonlinearities is achieved. This completes the proof.

Remark 4. From Eqs. (54) and (55), one has

5. Simulations

In this section,we demonstrate the proposed adaptive accurate tracking controllers for the longitudinal dynamic model of HFVs Eqs. (1) and (2). The model parameters of HFVs are borrowed from Ref.36. It is assumed that HFVs climb a maneuver from the initial trim conditions, listed in Table 1,to the final values V=8000 ft/s (1 ft/s=0.2048 m/s)and h=86000 ft. The velocity and altitude reference trajectories are through the following filters13

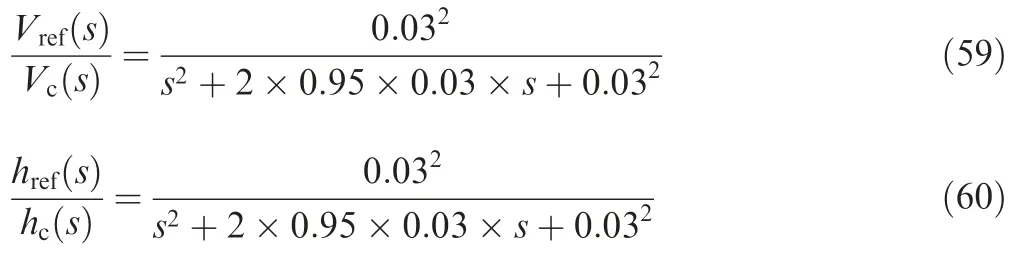
where Vref(s)and href(s)represent the inputs of filter,Vc(s)and hc(s) represent the inputs of filter. The design parameters are set as: kV=1, ςV=1, kh=kγ=kθ=kQ=2,

rV=rh=rγ=rθ=rQ=0.01, ςh=ςγ=ςθ=ςQ=2,cV=ch=cγ=cθ=cQ=0.0001. The time-varying function is chosen as ι(t )=1/(t2+0.1).In order to verify the effectiveness and advantages of the proposed method, the simulationtest of the proposed Adaptive Accurate Tracking Control(AATC) is compared with another conventional adaptive tracking control (CATC).17The cases of actuators dead-zone and hysteresis are also discussed, respectively.

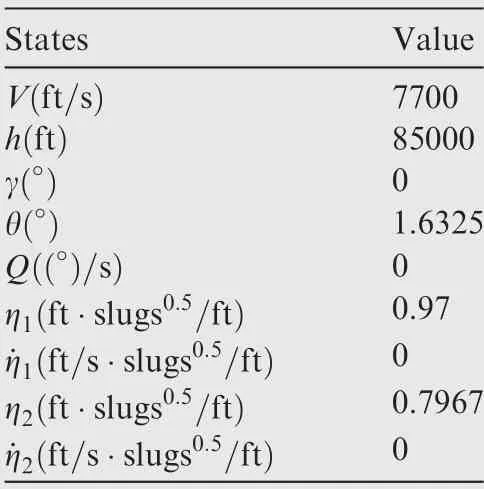
Table 1 Initial states.

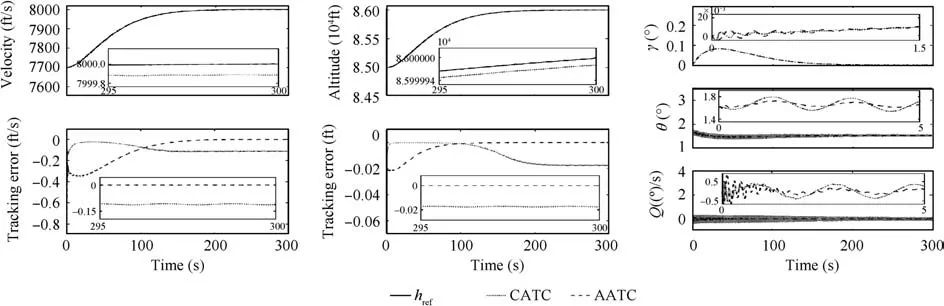
Fig 3 Velocity, altitude tracking performance and attitude angles with actuator dead-zone.

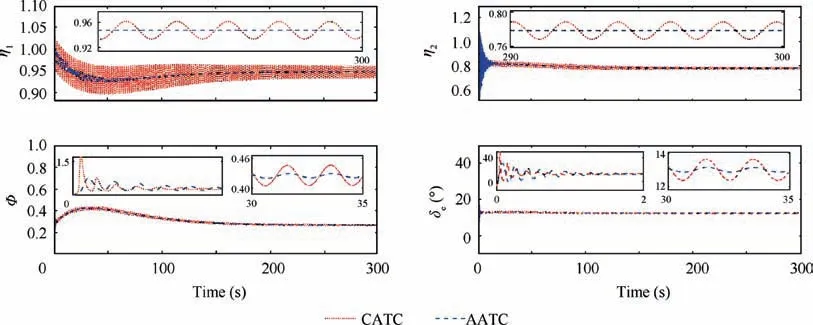
Fig 4 Flexible states and control inputs with actuator dead-zone.

Case 1. It is assumed that there exists dead-zone nonlinearity in actuators. The dead-zone models are expressed as

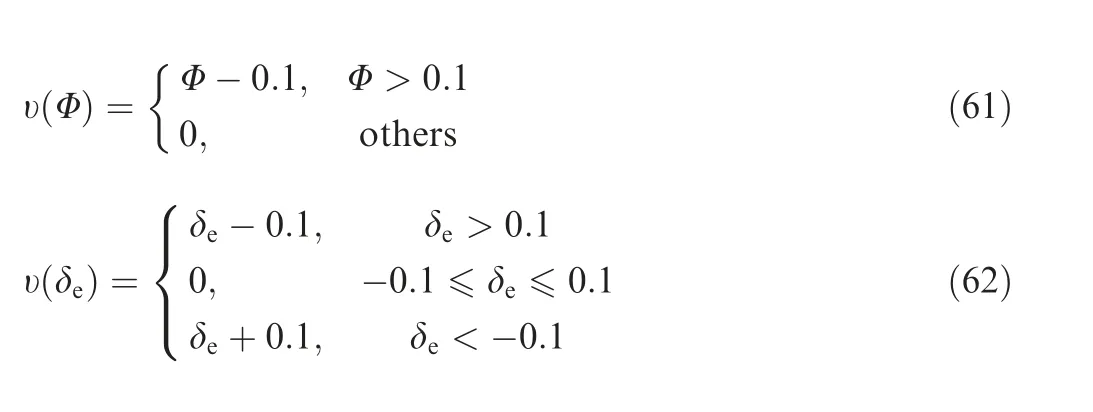
Fig 5 Velocity, altitude tracking performance and attitude angles with actuator hysteresis.

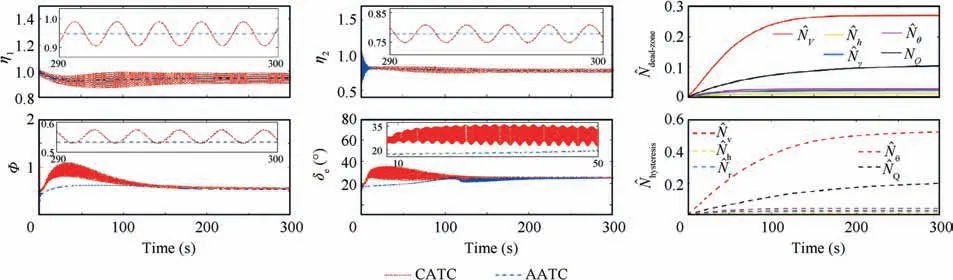
Fig 6 Flexible states and control inputs with actuator hysteresis as well as the value of ^N.

The obtained simulation results are depicted in Figs. 3 and 4. Fig. 3 reveals that the accurate tracking (i.e., the tracking errors of velocity and altitude asymptotically converge to zero)via the proposed AATC, while only the bounded error tracking (i.e., the tracking errors of velocity and altitude can converge to a residual set) via CATC. In addition, it can be seen in Figs. 3 and 4 that the AATC proposed in this work has the abilities to deal with the actuator input dead-zone nonlinearities.

It is observed from Figs. 3 and 4 that the attitude angles,flexible states, and control inputs obtained by AATC are smoother than the ones achieved by CATC, and there is no high frequency chattering based on AATC rather than CATC.Thus, the proposed AATC possesses better transient and steady performance.Case 2. In this case, the adverse situation that it appears hysteresis nonlinearity in actuators is considered. Consider the following hysteresis functions

Simulation results are presented in Figs. 5 and 6. From Fig. 5, it can be shown in Fig. 5 that the accurate tracking(tracking errors converge to zero) is obtained base on AATC rather than CATC, while CATC achieves bounded tracking errors. It can be observed from Figs. 5 and 6 that AATC has the capabilities to handle with actuator hysteresis. Moreover,it is seen that smoother trajectories of the attitude angles,the flexible states and the control inputs are achieved by AATC. Thereby the transient and steady performance of the exploited control strategy is better via AATC when the actuator hysteresis is taken into account. Further, the proposed AATC overcomes the shortcoming of high frequency oscillation issue. In addition, the adaptive parameter values of the devised AATC, both in the dead-zone and hysteresis condition, are bounded, as depicted in Fig. 6.

6. Conclusions

In this work, a novel adaptive accurate tracking controller,capable of coping with non-affine form of actuator nonlinearities such as dead-zone and hysteresis, is exploited for the longitudinal model of an HFVs effected by external disturbances.To overcome this barrier, non-affine form of actuator nonlinearity is transformed into affine form via mean value theorem.By means of a new back-stepping adaptive design,the velocity and altitude can accurately converge to zero in spite of actuator dead-zone and hysteresis.Besides,all signals of the closedloop system are guaranteed to be SGUUB. Finally, the effectiveness and superiority of the proposed approach are verified by simulation results.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgment

This work is supported by the Natural Science Basic Research Program of Shaanxi Province, China (No. 2019JQ-711).