中高频激励下轮轨不同建模方法对轮轨动态相互作用的影响

刘孟奇， 陶功权， 肖国放， 任德祥， 刘 欢， 温泽峰

(1.西南交通大学 牵引动力国家重点实验室，成都 610031； 2.中国中车株洲电力机车研究所有限公司，湖南 株洲 412001)

在现代铁路工程中，动力学数值模拟已成为分析铁道车辆运行时各部件动力学响应，研究车辆运行安全性、稳定性等方面的主要研究手段之一。随着铁道车辆运营速度不断提高、车辆逐渐轻量化及载重量不断提高，轮轨关系恶化严重，导致铁道车辆运营中车轮擦伤、多边形等异常磨耗非常普遍。车轮多边形磨耗或钢轨波磨容易导致轮轨系统出现中高频振动响应，此时对铁道车辆进行动力学仿真模拟的计算效率及计算可靠性提出了更高要求。因此，对铁道车辆动力学仿真模型展开深入研究具有十分重要的理论意义。

以往铁道车辆系统动力学模型受计算效率的限制或仅考虑低频范围内的动力学行为，通常将车辆-轨道系统中各部件视为刚体，不考虑其弹性变形，该方法建模流程简单且节省计算时间。如文献[1-2]利用车辆多刚体动力学模型研究了车轮失圆对铁道车辆动力学性能的影响。文献[3-4]通过车辆多刚体动力学模型分析了地铁车辆动力学性能。付彬等[5]基于地铁车辆动力学模型分析了车轮失圆状态下直线电机异常振动的原因。

随着铁路运输速度和载重量的不断提高、车辆结构逐渐向轻量化发展，轮轨系统间各部件自身的柔性特性对车辆-轨道系统轮轨动态相互作用的影响也变得不容忽视。因此，刚柔耦合多体动力学分析理论逐渐被引入到铁道车辆动力学分析中，将轮对和轨道等结构考虑为柔性体。文献[6-7]利用考虑轨道弹性变形的动力学模型对车轮扁疤进行了研究，结果表明车轮扁疤会激发高频与低频轮轨垂向力，并对扁疤深度限值进行了计算分析。Fermer等[8]基于实验与仿真对比了柔性轮对与刚性轮对车轮扁疤激励下的轮轨动态响应，结果表明柔性轮对由车轮扁疤引起的振动响应远小于刚性轮对。翟婉明等[9]对比分析了刚性和弹性轨道模型振动响应的差异。Gialleonardo等[10]建立了考虑不同轨道结构柔度的车辆-轨道系统动力学模型，研究指出忽略轨道结构柔性会高估车轮失圆状态下的轮轨动态力，考虑轨道结构柔性对20 Hz以内轮轨力频谱特性没有显著影响，但是20 Hz以上频谱特性相差很大。凌亮[11]对比不同轨道系统建模方式对车辆-轨道系统动力学响应的影响，指出忽略钢轨柔性动力学模型有效分析频率约为0～30 Hz，在随机轨道不平顺激励下忽略轨道板柔性会低估轮轨力低频振动响应而高估中高频振动响应。

近年来，随着计算机水平进一步发展，刚柔耦合动力学模型计算速度进一步加快，许多国内外学者不满足于仅将轮对或轨道等单一零部件考虑为柔性体建立动力学模型，多柔性体动力学模型得到进一步发展。宋志坤等[12-13]建立了考虑轮轨柔性的动力学模型，研究了车轮失圆和钢轨波浪形磨耗状态下的车辆动力学行为，发现模态共振导致柔性体振动幅值大于刚性体振动幅值，而远离模态共振时，柔性体产生的振动幅值小于刚性体振动幅值。杨光[14]基于旋转铁木辛柯梁及弹性多体动力学方法，建立了车辆-轨道系统动力学模型，研究了轮对旋转走行对车辆系统动力学性能的影响。Wu等[15-16]建立了车辆-轨道刚柔耦合动力学模型，分析了车轮扁疤、车轮多边形磨损引起的车辆系统动力学响应，结果表明模态共振能显著增加轴箱振动和轮对应力。

综上所述，研究车辆-轨道系统中高频激励下的响应时研究者们采用了不同复杂程度的动力学模型，比如多刚体动力学模型、考虑轮对或轨道单一部件柔性的刚柔耦合动力学模型、考虑轮对和轨道结构柔性的多柔性体动力学模型等，但并未对比分析轮对和轨道建模差异对仿真计算结果的影响，缺少与试验结果对比及针对某一特定零部件的柔性特性分析。因此，为了明确中高频激励下动力学仿真分析时轮轨建模对计算结果及计算效率的影响，本文根据轮对、轨道结构实际参数及地铁车辆悬挂参数建立相应的车辆-轨道系统耦合动力学模型，通过试验数据验证模型准确性。将实测车轮多边形磨耗及谐波多边形磨耗作为输入，对比分析中高频激励下轮对、轨道结构不同建模方式对轮轨动态相互作用、车辆-轨道系统振动响应的影响，结合不同模型计算结果准确性和计算效率为今后动力学数值仿真模型的建立提供一些参考。

1 地铁车辆-轨道耦合动力学模型

基于动力学仿真软件SIMPACK建立B型地铁车辆多刚体动力学模型。在有限元软件ANSYS中建立轮对、轨道结构有限元模型，并进行子结构分析。利用SIMPACK中FEMBAS、FLEXTRACK接口，实现轮对、轨道结构柔性化。车辆-轨道刚柔耦合动力学模型如图1所示。图1(a)为地铁车辆多刚体动力学模型，图1(b)为美国五级谱钢轨不平顺激励，图1(c)为柔性轮对模型，图1(d)为实测B型地铁车辆多边形磨耗，图1(e)为柔性轨道结构模型。

图1 车辆-轨道刚柔耦合动力学模型Fig.1 Vehicle-track rigid-flexible coupled dynamics model

1.1 地铁车辆多刚体动力学模型

根据某B型地铁车辆悬挂参数，利用SIMPACK多体动力学软件建立地铁车辆动力学模型，模型包括1个车体、2个构架、4个轮对以及8个轴箱，共15个刚体，其中车体、构架和轮对结构均具有纵向、横移、沉浮、侧滚、点头、摇头6个自由度，轴箱只有点头自由度，共50个自由度。一系悬挂为叠层橡胶弹簧，二系悬挂包括2个大阻尼的空气弹簧、单侧横向减振器、2个中心对称的牵引拉杆以及横向止挡。各部件间通过力元的形式进行连接，横向止挡和横向减振器均考虑其非线性特性。车轮踏面采用LM型面，钢轨为中国60 kg/m型面(CN60)。车轮与钢轨间通过HERTZ接触算法计算轮轨法向力，采用KALKER简化理论FASTSIM算法对轮轨切向力进行求解。

1.2 轮对柔性化

动力学分析软件SIMPACK将刚体单元视为1个独立自由度的节点和多个非独立自由度的节点，刚体单元的运动通过在独立自由度节点上施加铰接、力元、动力学约束等实现[17]。柔性体单元则由具有3个方向位移或转动自由度的主、从节点组成，通过主节点确定与其他部件的联系。柔性体在SIMPACK中变形的计算是通过模态叠加来实现的。因此若要实现轮对结构柔性化，须建立轮对有限元模型并对其进行模态分析。考虑到计算效率的问题，还要进行一定程度的主自由度缩减，即子结构分析。轮对有限元模型中弹性模量为210 GPa，泊松比为0.28，密度为7 800 kg/m3。利用Block Lanczos法对轮对有限元模型进行模态分析，利用Guyan缩减法[18]求得轮对结构的缩减矩阵解。在ANSYS子结构分析中，选择取轮对模型的主节点。在车轴处选取11个截面共55个主节点，车轮踏面位置选2个截面共80个主节点，辐板位置选取2个截面共80个主节点，所选取的节点总数为215个，如图2所示，图中三角箭头部分为所选取的主节点。结合SIMPACK中FE模块生成包含轮对质量、刚度等信息的柔性体文件。轮对进行主自由度缩减前后计算结果如表1所示，主自由度缩减前后轮对模态频率变化较小。

图2 轮对子结构模型Fig.2 Substructure model of wheelset

表1 轮对模态计算结果

1.3 轨道结构柔性化

本文根据中国60 kg/m钢轨截面建立钢轨有限元模型，将钢轨考虑为Timoshenko梁，采用Beam 44单元划分网格，并进行子结构分析。子结构分析时钢轨轨底每隔0.6 m选取1个主节点用以施加扣件力元，轨头每隔0.3 m选取1个主节点。普通整体道床有限元模型采用实体单元Solid 185离散，道床简化考虑为平行六面体结构，其尺寸为12.5 m×5 m×0.3 m。弹性模量为32.5 GPa，泊松比为0.24，密度为2 400 kg/m3。道床子结构分析时选取顶面及底面部分节点作为主节点，且需注意要保证道床与钢轨扣件连接处必须选取主节点，以方便建立扣件力元约束，钢轨及道床子结构模型如图3所示。利用弹簧阻尼力元模拟扣件约束，扣件力元包含3个方向刚度和阻尼，同时为模拟钢轨翻转现象还定义了绕纵向的扭转力矩。利用MATLAB软件编写FLEXTRACK配置文件，文件中包含钢轨、轨道板模型信息、主节点空间位置信息、扣件刚度和阻尼、轨道板与地基间约束等信息。最后利用SIMPACK中FLEXTRACK模块读取编写的配置文件，修改轮轨接触关系并重新装配，以实现轨道结构的柔性化。仿真分析时，钢轨考虑了500 Hz以内的模态，道床模态取前20阶，对应振动频率198 Hz。钢轨和道床端部利用力元进行固定，根据SIMPACK用户手册推荐，取其纵向、横向、垂向刚度均为1×1010N/m，阻尼均为1×107N·s/m。扣件刚度、道床与地基间约束刚度设置如表2所示。

图3 轨道结构子结构模型Fig.3 Substructure model of track

表2 轨道结构部分参数

采用FLEXTRACK模块建立轨道结构模型时，可以重复引用柔性体文件。本文建立了12 m长钢轨和道床有限元模型，在配置文件中重复引用，建立了48 m长柔性轨道结构模型。

2 模型验证

基于现场试验测试，从轨道结构位移、车辆结构振动及B型地铁P2共振频率计算3个部分对模型进行验证。

利用激光位移传感器对直线段普通扣件整体道床的钢轨动态位移进行测试。仿真计算时，直线工况AW0状态下车速为52 km/h，与试验时车速一致，考虑轨道随机不平顺激励。图4为仿真计算得到的不同扣件位置钢轨垂向位移结果对比。图中扣件1～5分别对应柔性轨道结构前5个扣件，通过对比可发现，轨道结构边界效应仅对前2个扣件有一定影响，影响范围不足2 m，第3个扣件之后钢轨垂向位移基本相同。

图4 不同扣件钢轨垂向位移Fig.4 Vertical displacements of rail at different fasteners

图5为试验测试与仿真结果对比分析。通过对比研究可以发现，地铁车辆-轨道耦合动力学模型各轮对通过时钢轨垂向位移的波形和幅值均与现场试验结果吻合较好，计算和测试得到的钢轨垂向位移最大值分别为0.382 mm和0.352 mm，误差约为8.5%。对比验证结果表明本文建立的轨道结构模型准确性较高。

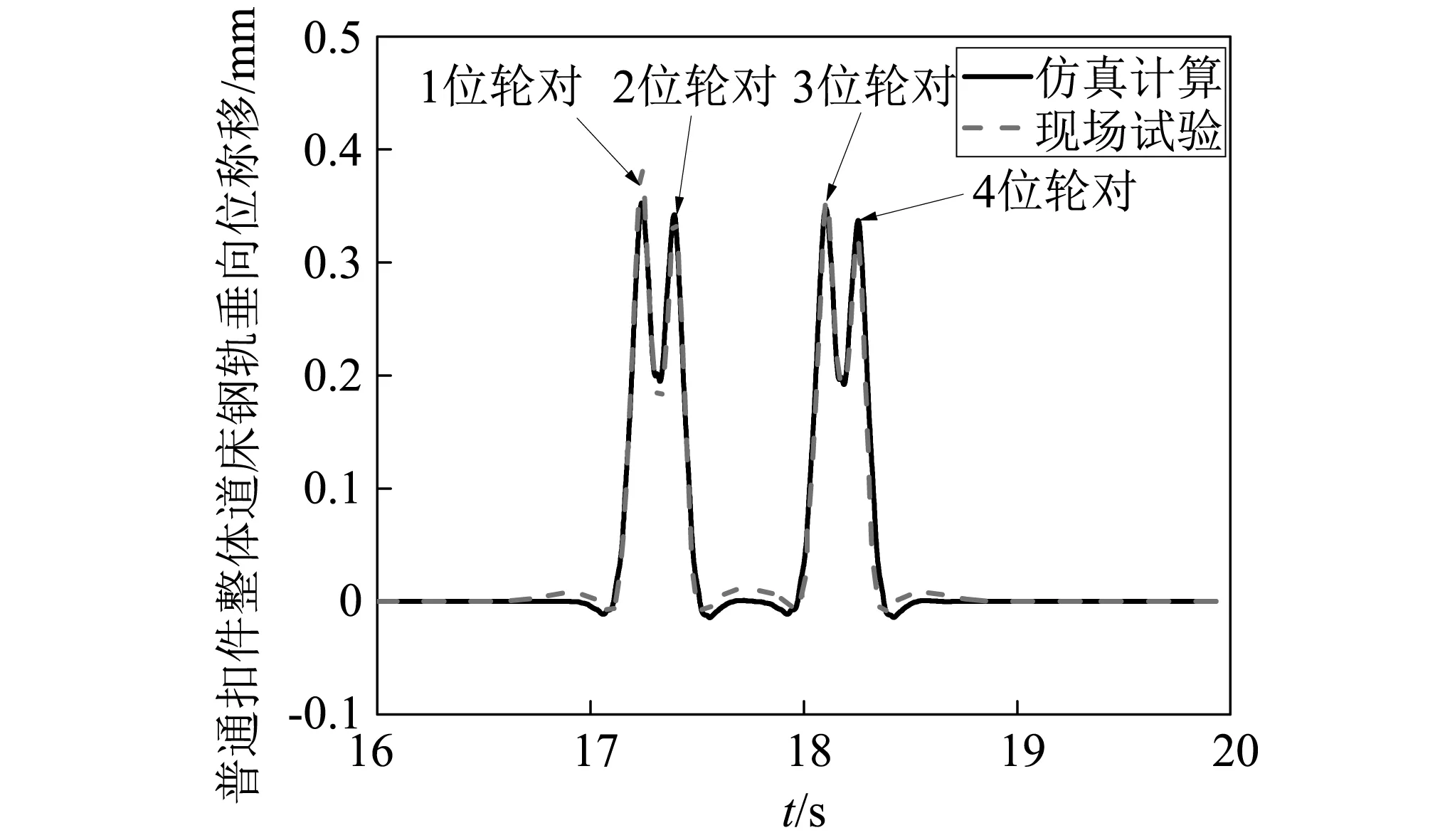
图5 普通整体道床钢轨垂向位移Fig.5 Rail vertical displacement

分析考虑轮对、轨道结构柔性的耦合动力学模型在实际车轮失圆状态下的轴箱振动加速度响应，并与现场试验测试结果对比，进一步验证地铁车辆-轨道耦合动力学模型的准确性。仿真计算时，地铁车辆运行速度为75 km/h，采用直线工况，车辆为AW0状态，不考虑轨道不平顺的影响。

图6为现场试验测试得到的某地铁车辆车轮不圆度测试结果，其中图6(a)为极坐标图，反映了车轮径跳沿圆周的变化；图6(b)为车轮不圆度的阶次图，是将测试结果窄带粗糙度谱分析后的结果，能客观反映各个阶次粗糙度水平。通过测试结果可以看出该车轮不圆度径跳值较大，接近0.6 mm，车轮存在比较严重的偏心和6阶多边形，其中6边形粗糙度水平较高，超过了40 dB。

车轮多边形通过频率与车轮多边形阶次关系表示为

(1)

式中：f为多边形通过频率；v为车辆运行速度；D为车轮直径；n为多边形阶次。当地铁车辆运行速度为75 km/h时，6边形的通过频率约为48 Hz。

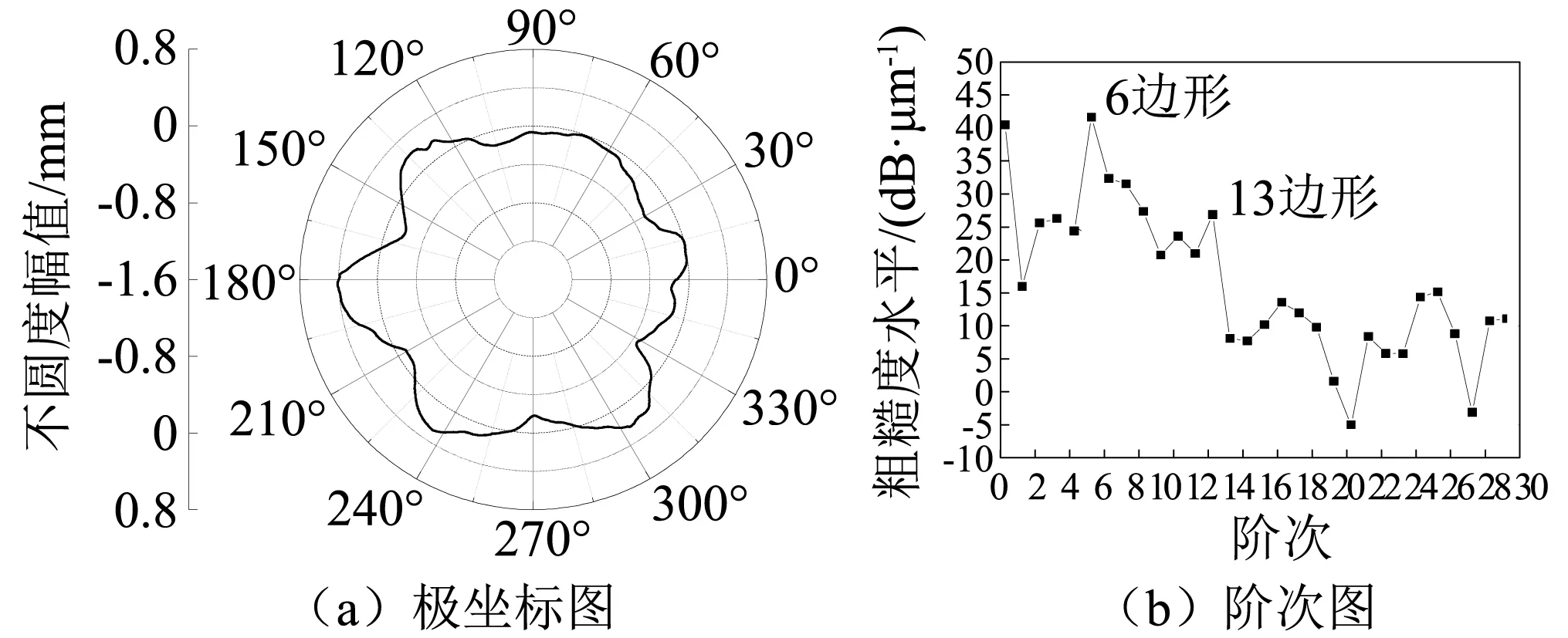
图6 车轮不圆度测试结果Fig.6 Wheel out-of-roundness measurement results

以图6所示的车轮不圆度测试结果作为输入，图7给出了地铁车辆-轨道耦合动力学模型在实测车轮失圆状态下的仿真结果，并与现场试验结果对比。试验得到的轴箱垂向加速度有效值约为54 m/s2，而通过仿真计算得到的轴箱垂向加速度有效值约为48 m/s2，与实际情况比较接近。

对轴箱加速度时域结果进行傅里叶变换，得到轴箱垂向加速度频谱图，如图7(b)所示。试验测试结果与仿真结果在0～400 Hz内频谱特性基本一致，均在48 Hz，64 Hz和102 Hz存在明显的峰值。通过图5车轮多边形测试结果可知，试验测试车轮存在比较明显的6边形及13边形，在车速75 km/h工况下，对应的多边形通过频率恰好为48 Hz和102 Hz。

进一步分析模型在64 Hz存在明显主频的原因。通过轮对、轨道结构的有限元模态分析，可知轮对扭转、一阶弯曲模态及钢轨1阶、2阶垂向弯曲模态均远大于64 Hz。相关文献研究结果表明轮轨系统P2共振频率约为20～100 Hz[19]。因此建立了图8(a)所示簧下质量-轨道结构耦合系统有限元模型，其中轮轨之间通过弹簧单元模拟其接触，接触刚度取1.524×109N/m[20]，轮对质量为1 290 kg。考虑到轮对和轨道结构的对称性，仅选取半条轮对和一半轨道结构进行计算，并对道床和轮对对称中面施加对称约束。通过模态分析计算得到系统P2力共振频率如图8(b)所示，计算结果显示地铁车辆簧下质量与轨道结构耦合共振频率约为63.4 Hz。因此，图6中64 Hz的振动为轮轨系统P2共振。

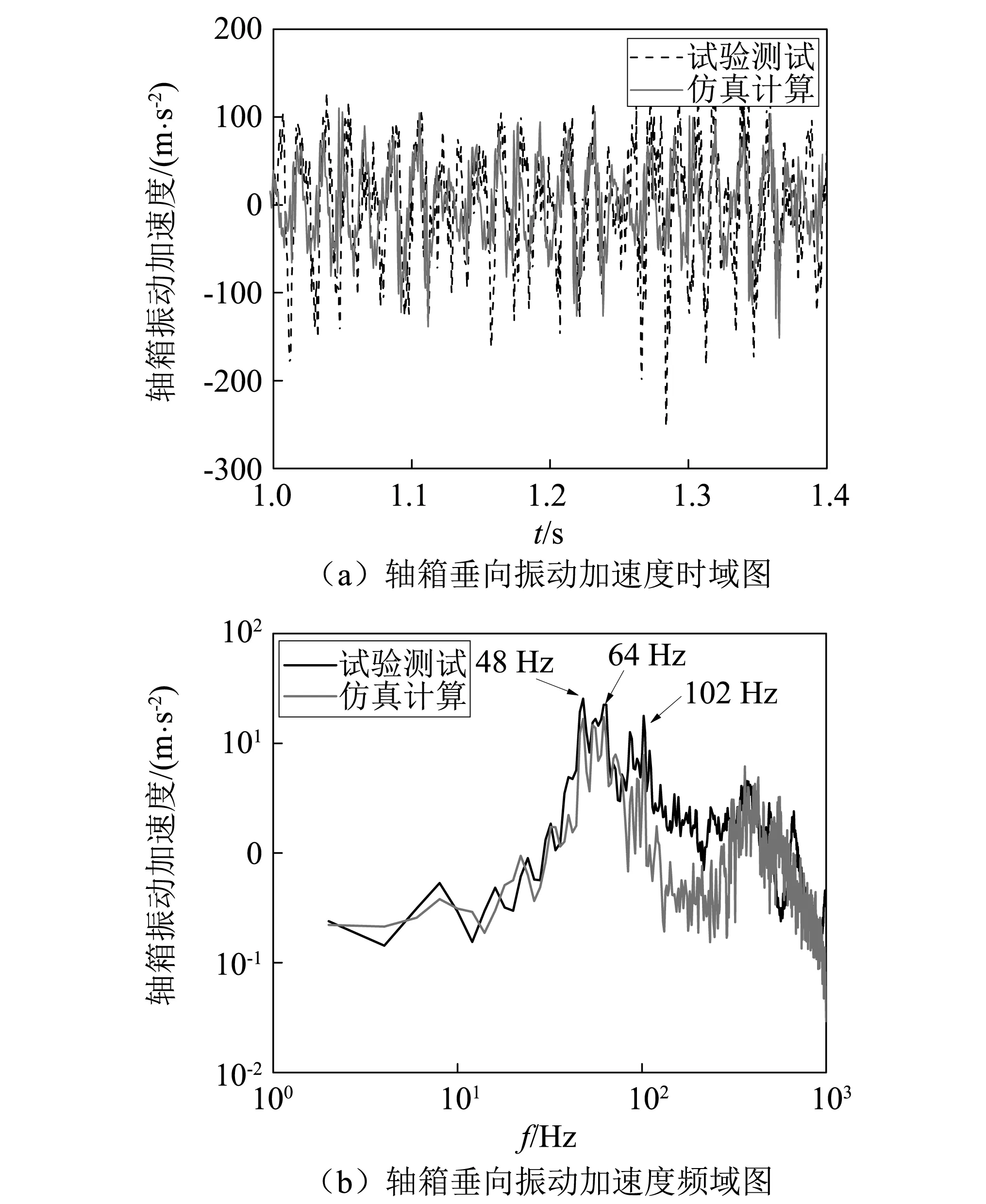
图7 试验结果与仿真结果对比Fig.7 Comparison of experimental and simulation results

通过以上时域和频域结果对比可知，本文建立的地铁车辆-轨道耦合动力学模型与实际车辆比较接近，模型准确性较高，可以用于该地铁车辆轮轨动态相互作用的仿真计算。

3 车轮非圆化磨耗激励下不同模型轮轨动态相互作用的对比分析

本节着重对比车轮失圆状态下不同模型轮轨动态响应，研究不同模型建模优势与适用范围。为对比中高频轮轨激励下不同模型轮轨动态相互作用的差异，本文基于多刚体动力学模型和轮对、轨道结构有限元模型建立了4种地铁车辆动力学模型，如表3所示。

表3 不同模型建模差异

图8 簧下质量轨道结构耦合模型及计算结果Fig.8 Coupled model of unsprung mass and track structure and its calculation results

3.1 实测车轮多边形磨耗激励

仿真计算时，直线工况AW0状态下设置车辆运行速度为75 km/h，不考虑轨道随机不平顺。不同模型所有车轮均施加图6所示的车轮多边形磨耗激励。以导向轮对右侧车轮为例，对比不同模型之间的差异。不同模型车轮失圆状态下轮轨垂向力时域及频域结果，如图9所示。通过对比可以发现，不同模型在计算过程中均出现了周期性的轮轨分离。模型1轮轨垂向力的有效值最大，约为61 kN；模型2的轮轨垂向力有效值约为54 kN，相比模型1轮轨力有效值降低了11.5%；模型3的轮轨垂向力有效值约为45 kN，相比模型1轮轨力有效值降低了26.2%；模型4的轮轨垂向力有效值约为42 kN，相比模型1轮轨力有效值降低了31.1%。模型中考虑轮轨结构弹性变形可显著减小轮轨间相互作用力，这是由于考虑轮对、轨道结构柔性变形能吸收部分轮轨间冲击载荷，对地铁车辆及轨道结构振动起到一定衰减作用。

轮轨垂向力频域分析结果表明，模型1在100～500 Hz存在明显主频，且每个频率间隔8 Hz，约为车轮转动一周频率，这是由于车轮、轨道结构均没有考虑其弹性变形，产生了倍频激扰，高估了高频部分轮轨垂向力；模型2在200～500 Hz存在明显主频，但其各频率的幅值均小于模型1，这是由于考虑了轮对结构的弹性变形，吸收了部分轮轨间振动能量所致。模型3与模型1计算结果存在明显差异。在30～100 Hz，模型3其幅值明显高于模型1，而在150 Hz以上高频范围部分没有出现明显主频。模型3在48 Hz、64 Hz、102 Hz处轮轨力峰值较大，通过多边形测试可知该车轮6阶、13阶多边形磨耗严重，其多边形通过频率为48 Hz和102 Hz。而64 Hz处轮轨力较大则为多边形通过频率激发了轮轨系统P2力共振所致。导致上述差异的根本原因在于轨道结构建模方式的不同，考虑轨道结构柔性动力学模型考虑了弹性、阻尼轨道结构体系参振，一方面可以吸收部分轮轨高频振动能量，另一方面能准确向上反馈轨道结构振动响应。在模型3基础上，模型4考虑了轮对结构柔性变形，进一步降低了轮轨间振动能量，但其频率特性基本不变。

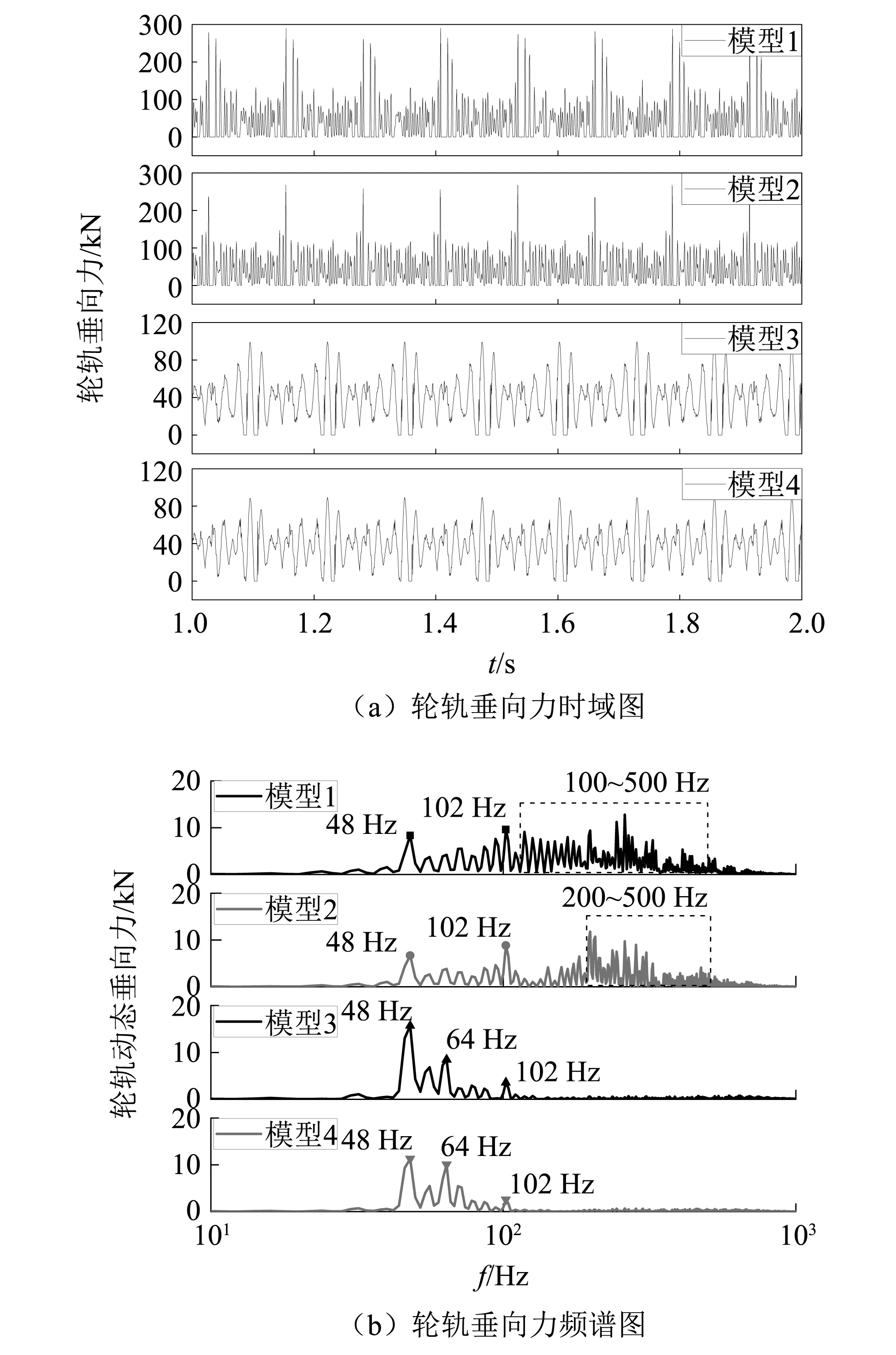
图9 车轮多边形激励下的轮轨垂向力响应Fig.9 Wheel-rail vertical force under excitation of wheel polygonal wear

图10所示的轮轨横向蠕滑力时域和频域特性也有与轮轨垂向力类似的结论。总体来说，考虑轮对、轨道结构柔性均能显著降低轮轨动态垂向力、横向蠕滑力等轮轨间动态相互作用，且能准确反映轮轨系统模态共振的现象。结合车轮多边形磨损状态及轴箱加速度振动响应，模型1和模型2其高频部分计算存在较大误差，模型3和模型4其计算结果更加符合实际情况。

图10 车轮多边形磨耗激励下的轮轨横向蠕滑Fig.10 Wheel-rail lateral creep under excitation of wheel polygonal wear

3.2 车轮谐波多边形磨耗激励

为进一步对比车轮不同失圆状态下不同模型轮轨动态相互作用的差异。以不同阶次和波深的谐波多边形磨耗作为输入，分析对比不同动力学模型计算结果之间的差异。

谐波激扰可采用下式进行描述[21]

(2)

(3)

式中：a为不平顺波深；L为不平顺波长；n为谐波激扰数。以相同波深不同阶次的谐波多边形磨耗作为输入，对比4种模型轮轨动态相互作用的差异。仿真计算时，直线工况AW0状态下地铁车辆运行速度为75 km/h，谐波多边形波深均为0.2 mm，多边形阶次为3～15。不同模型轮轨垂向力计算结果，如图11(a)所示。由图11(a)可知，随着多边形阶次增大，模型1和模型2轮轨垂向力最大值呈线性增长。当多边形阶次大于14时，地铁车辆运行时会出现周期性轮轨分离，两模型轮轨垂向力随波深变化的斜率激增，且模型2斜率略小于模型1，这是由于轮对弹性变形吸收部分高频振动能量所致。模型3与模型4则呈现出先增大后减小的趋势，在8阶多边形失圆状态下轮轨垂向力最大，接近80 kN，此时多边形通过频率约为64 Hz，激发了簧下质量与轨道结构耦合共振。此外当多边形阶数小于4时，4种动力学模型计算结果差异较小。以4阶谐波多边形磨耗为例，该工况下4种模型仿真得到轮轨力最大值分别为41.05 kN，40.70 kN，42.20 kN，41.61 kN，计算结果非常接近。随着多边形阶次增大，不同模型计算结果差异较大。

为分析不同轮轨建模方式车轮多边形磨耗下振动响应差异，对轴箱加速度RMS值进行对比分析，如图11(b)所示。由计算结果可知，模型1轴箱加速度均方根值与多边形阶次呈线性递增的趋势；模型3和模型4其轴箱加速度均方根值呈现先增大后减小趋势，这点与轮轨垂向力随多边形阶次变化规律呈现一致性。当车轮为11阶谐波磨耗时，模型2出现明显峰值。车轮11阶谐波磨耗条件下，多边形通过频率为88 Hz，激发了柔性轮对约束状态下一阶垂向弯曲模态(约为90.55 Hz)，导致轮对结构发生共振，轴箱加速度产生较大波动。考虑轮对结构柔性能较好的反映客观实际中存在的模态共振，结果更真实准确。当谐波多边形阶数小于4时，4种模型计算结果相差很小；当多边形阶数增大，不同模型结算结果误差较大，该现象与轮轨力对比结果一致。根据式(1)可计算得到4阶谐波多边形通过频率为32 Hz，因此可认为模型1和模型2有效分析频率为0～30 Hz，高频计算结果存在较大误差。

图11(c)和图11(d)分析了不同模型随多边形阶次变化轮轨横向蠕滑力/率结果的差异。结果显示不同模型随多边形阶次变化轮轨横向蠕滑力变化规律与轮轨垂向力大致相同。随着多边形阶次增大，模型1和模型2轮轨横向蠕滑力RMS值呈现指数型增长，模型3与模型4则呈现出先增大后减小的趋势。通过对比分析轮轨横向蠕滑率可发现，轮轨横向蠕滑率和横向蠕滑力变化规律一致。进一步分析发现，模型3、模型4在8～10边形磨耗时，轨头位置横向加速度有效值较大，导致钢轨产生绕质心的翻转运动，车轮踏面与钢轨产生动态横向相对运动，因此车轮产生较大的横向蠕滑，进而导致轮轨间横向蠕滑力较大。

通过以上对比分析可以得出，车轮、轨道结构建模方法的不同导致车轮失圆状态下轮轨力及振动响应产生了明显的差异。模型1和模型2有效分析频率为0～30 Hz，高频计算结果存在较大误差，不考虑轨道结构柔性会高估轮轨间高频振动响应。此外模型2考虑轮对结构柔性能较好地反映实际中存在的轮对结构模态共振。模型3和模型4考虑轨道结构柔性能切实反映实际中存在的簧下质量与轨道结构耦合共振，而这种轮轨系统耦合共振(P2共振)在地铁运营现场普遍存在[22]，通常也是地铁车轮产生多边形磨耗和钢轨波磨的主要原因。因此对地铁车辆进行中高频动力学分析时，考虑轮轨柔性是非常有必要的。

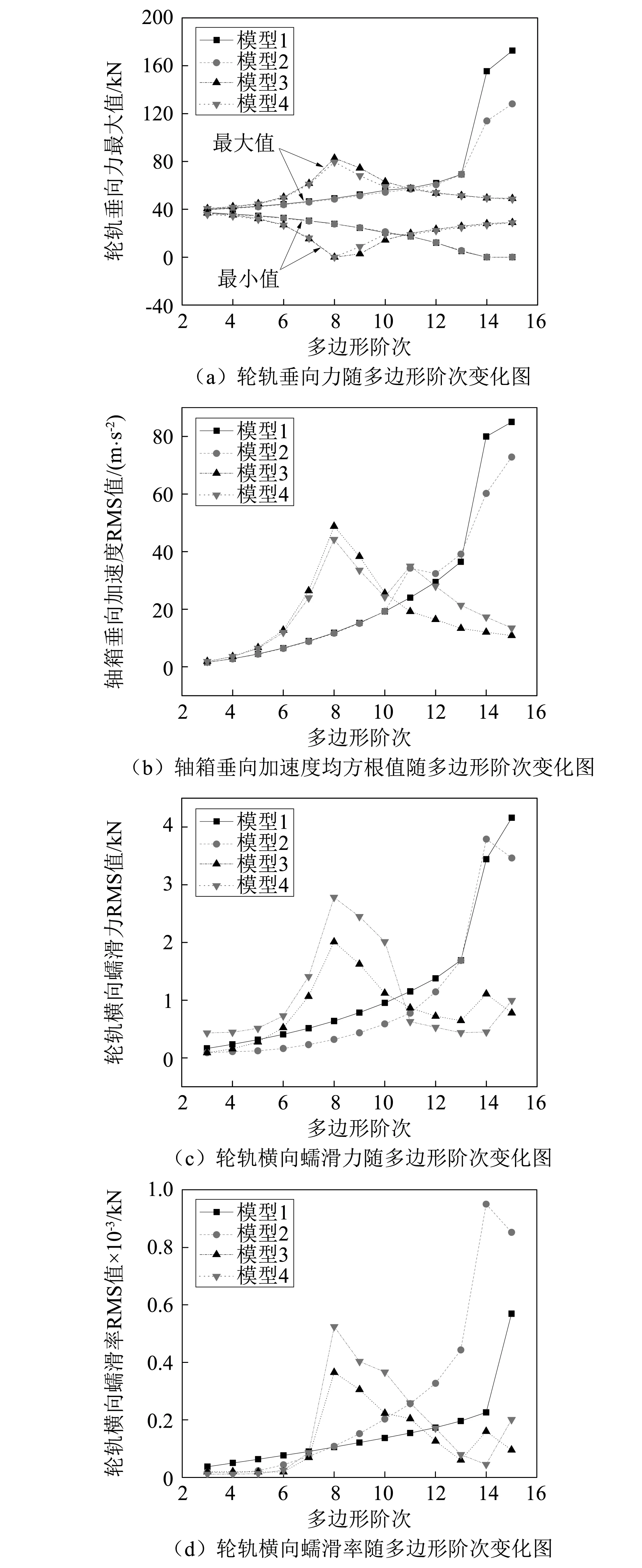
图11 不同模型动力学响应Fig.11 Dynamic responses of different models

上文针对不同模型计算结果进行了详细对比分析，而仿真分析时计算效率也是需要考虑的。表4对比了4种不同模型在车轮实测多边形磨耗激励下计算效率的差异。模型1不考虑轮轨柔性变形，计算效率最高。模型2考虑轮对柔性变形，虽然选取了大量主自由度点，但仅有踏面位置80个主节点和一系悬挂位置2个主节点参与动态响应计算，其他主节点仅参与轮对模态计算，因此模型2计算时间变化不大，计算时间约为模型1的1.7倍。模型3考虑轨道结构柔性变形，其中钢轨取前500 Hz模态，道床模态取前200 Hz模态，叠加模态阶数多，且所有主节点(共851个)均参与动态响应计算，因此计算效率显著降低，计算时间约为模型1的37.7倍。模型4在模型3基础上考虑了轮对柔性，其计算时间约为模型1的61.0倍。本文计算结果也为以后动力学仿真时模型建立提供参考。

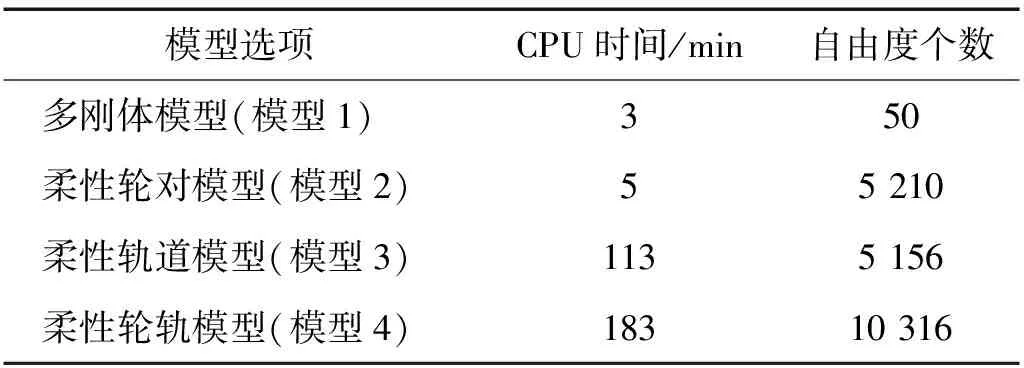
表4 不同模型CPU计算时间 (CPU参数Inter Core i7-7700 3.6 GHz)

4 结 论

建立了考虑轮对、轨道结构柔性的地铁车辆刚柔耦合动力学模型，利用轨道位移试验和地铁车辆振动试验结果验证了模型的准确性。重点分析了轮对、轨道结构不同建模方式车轮失圆状态下轮轨间动态相互作用的差异。主要结论如下：

(1) 实测典型5～8阶车轮多边形磨耗激励下考虑轮对柔性动力学模型、考虑轨道结构柔性动力学模型及考虑轮轨柔性动力学模型相比于传统多刚体动力学模型，轮轨垂向力有效值分别降低了11.5%，26.2%和31.1%。

(2) 多刚体动力学模型与考虑轮对结构柔性动力学模型有效分析频率较低，仅为0～30 Hz，其高频计算结果存在较大误差，但考虑轮对柔性模型能较好的反映轮对固有模态响应。考虑轨道结构柔性的动力学模型和考虑轮对、轨道结构柔性的动力学模型其计算结果能较准确的反映实际情况，其中考虑轮轨柔性模型结果更加准确。

(3) 多刚体动力学模型不考虑轮轨柔性变形，计算速度快，建模流程简单。考虑轮对结构柔性动力学模型计算约为多刚体动力学模型的1.7倍。考虑轨道结构柔性的动力学模型和考虑轮对、轨道结构柔性的动力学模型由于叠加模态阶数多且大量主节点参与动力学计算，建模流程相对复杂，模型计算速度慢，其计算时间分别为多刚体模型的37.7倍和61.0倍。

(4) 动力学仿真计算时，采用多刚体动力学模型和考虑轮对柔性动力学模型分析车辆系统低频动力学响应(如轨道随机不平顺激扰下车辆平稳性舒适性)是行之有效的，且计算效率高。若需分析中高频(30 Hz以上)动力学响应，建议采用考虑轨道结构柔性动力学模型和考虑轮对、轨道结构柔性的动力学模型，其计算结果更精确。