不同梁线刚度情形下组合梁柱子结构抗倒塌性能研究

谭 政， 钟炜辉,2， 段仕超， 孟 宝， 郑玉辉， 宋晓燕

(1. 西安建筑科技大学 土木工程学院，西安 710055；2. 西安建筑科技大学 结构工程与抗震教育部重点实验室，西安 710055)

建筑结构因偶然荷载作用(撞击、爆炸、地震以及火灾等)引起的结构整体倒塌，会造成严重的生命财产损失，近年来关于结构抗倒塌的研究已成为土木工程界的研究热点。目前，研究框架结构在连续倒塌工况下的受力性态，一般采用备用荷载路径法(拆柱法)[1]进行，该方法不考虑竖向承重构件的失效过程和原因，只考虑与失效柱相连的主要构件在外载作用下的性态变化。当局部竖向构件失效后，剩余结构的荷载传力路径将发生改变，原本作用于失效柱的荷载可通过内力重分布作用将其上方框架的部分荷载转由与失效柱相连的双跨梁承担。此时，双跨梁首先通过梁机制传递荷载，并在竖向结构发生大变形的过程中悬链线机制逐渐显著并替代梁机制抵抗外载。而悬链线机制的发挥主要取决于梁柱构件的拉结作用和梁柱节点的转动能力，GSA标准[2]和CECS 392—2014《建筑结构抗倒塌设计规范》[3]规定当失效柱竖向相对位移超过梁跨度的1/5时作为结构的倒塌失效位移准则。但大量研究成果[4-5]表明，该倒塌失效准则过于保守，因此有必要提出一种更为准确的失效准则以判定结构是否发生破坏。

史艳莉等[6]采用双半跨梁柱子结构形式，以圆钢管混凝土柱-H钢梁内隔板式节点为研究对象，分析了钢梁强度，混凝土强度等参数对结构抗倒塌性能的影响；Yang等[7]在考虑组合楼板作用的情形下，以平齐端板连接和腹板双角钢连接的两跨三柱梁柱子结构进行试验，研究了组合梁柱子结构在中柱失效工况下的破坏模式和传力机制，分析表明，组合框架结构梁柱节点性能对抗力影响显著；Weng等[8]根据失效位置，进行了边柱失效和内柱失效的混凝土梁柱子结构抗倒塌试验，结果表明，可靠的边界条件是有效发挥悬链线机制的必要条件；Zhong等[9]以钢框架中三种不同连接节点形式(栓焊连接、顶底角钢腹板双角钢连接和腹板双角钢连接)的两跨三柱型梁柱子结构为研究对象，通过对中柱施加静力荷载考察了梁柱子结构在中柱失效连续倒塌条件下的抗倒塌机理，结果表明顶底角钢腹板双角钢连接试件在后期更能充分发展梁端节点转角和梁截面轴力，表现出更为富余的抗倒塌能力；Loh等[10]为研究组合楼板作用对结构抗倒塌性能的影响，进行了五个外伸端板连接节点和纯钢节点试验研究，试验结果表明楼板的存在有利于提升结构的抗倒塌承载能力，并随着配筋率的增大提升效果更趋显著，较低的配筋率会导致混凝土板严重开裂，合理的配筋范围为1.0%～1.5%。截止目前，关于框架结构梁柱子结构抗倒塌机制的研究主要集中在节点类型、失效柱位置、楼板组合作用、子结构形式和楼板配筋率等方面，而关于组合梁线刚度这一重要参数的研究极为有限，而且既有研究主要都是开展结构性能方面的研究，对于结构抗力贡献定量化评估的研究极为有限，故难以给工程设计和实际应用可操性的指导意见。在倒塌过程中组合梁的线刚度对结构梁机制和悬链线机制的发挥都具有极大影响，所以有必要针对组合梁不同线刚度对结构抗倒塌性能的影响进行深入分析。

本文针对组合梁柱子结构抗倒塌研究存在的不足，建立了不同组合梁线刚度情形下组合梁柱子结构的相关模型，并利用前期完成的试验对模型进行了验证。基于此模型，详细分析了组合梁不同线刚度对结构倒塌性能的影响。由于目前倒塌判定准则存在一定的缺陷，对目前基于变形的结构倒塌失效判定准则进行修正，定量的分析了不同梁线刚度情形下梁机制和悬链线机制对结构抵抗外载的贡献水平，可为结构抗倒塌设计规范的修订和完善提供依据。

1 有限元模型的建立和验证

1.1 有限元模型概述

参考GB 50017—2017《钢结构设计标准》[11]，设计了尺寸如图1(a)所示的原型结构，其中，主梁和次梁分别为4.5 m和7.5 m，层高为3.3 m。在框架结构抗倒塌分析中，通常将失效柱的上方楼层以及与失效柱相连的两跨定义为直接影响区，其他区域定义为间接影响区[12]。直接影响区是抗倒塌研究和设计的重点，间接影响区则为直接影响区提供可靠的边界条件。本文采用两跨三柱型梁柱子结构模型进行抗倒塌性能分析，其边柱的反弯点近似位于其层高中部。为考虑间接影响区对组合梁柱子结构抗倒塌性能的影响，结合组合梁反弯点的位置，在外伸梁伸出边柱1/4L处作为边界[13]，将反弯点处简化为铰接，如图1(b)所示。

图1 组合梁柱子结构的选取Fig.1 Selection of composite beam-column substructure

钢材均采用Q235级钢，子结构的梁柱截面分别为H450×300×11×18(mm)、H400×400×13×21(mm)。钢梁腹板通过剪切板与柱翼缘相连，其中剪切板为110×12(mm)，采用10.9级M22的高强螺栓。根据FEMA[14]标准推荐，本文采用盖板加强型连接节点，节点的细部构造如图2所示。混凝土强度等级为C25，有效宽度为1 500 mm，楼板厚度为100 mm，保护层厚度为20 mm，楼板的有效宽度为1 500 mm，纵向钢筋为φ14@150，分布钢筋为φ8@200，受力钢筋与分布钢筋形成钢筋网，楼板内设置两层钢筋，具体布置如图2(d)所示。钢梁和组合楼板之间选用φ19的栓钉作为抗剪连接件，并设置为双排，间距为210 mm，排距为150 mm，满足完全抗剪连接要求。

图2 节点详图和配筋布置(mm)Fig.2 Details of connections and distribution of reinforcement(mm)

1.2 有限元分析模型建模方法

采用软件Abaqus/Explicit动力显示积分算法对组合梁柱子结构进行非线性有限元分析，在失效柱柱顶施加位移，对应幅值属性为平滑分析步，仅允许失效柱竖向移动；由于边柱顶部仍承受上部荷载作用，为更为真实的反应子结构的受力特征，在边柱顶部施加0.3的轴压比对应荷载来模拟上部荷载作用，并且限制边柱顶部的水平和平面外位移；边柱下端边界条件则设置为铰接。试件主要部件包括钢梁、钢柱、混凝土板、钢筋、螺栓、压型钢板、节点剪切板以及盖板等，采用三维桁架单元T3D2模拟楼板中的钢筋，对于其余部件均采用C3D8R实体单元进行建模，并在节点应力集中区域划分较密的网格单元。钢材屈服强度fy取为235 MPa，抗拉强度fu取为353 MPa，采用二次流塑四阶段模型本构，弹性模量E取2.06×105MPa，如图3(a)所示；螺栓的屈服强度为940 MPa，抗拉强度为1 130 MPa；钢筋采用HPB300热轧钢筋，fy取为300 MPa，fu取为420 MPa，采用双折线强化本构如图3(b)所示；混凝土强度等级为C25，选用Abaqus中的塑性损伤模型，根据GB 50010—2010《混凝土结构设计规范》[15]附录C，其受压和受拉应力-应变关系如图3(c)所示。为模拟试件的断裂过程，采用Abaqus中的延性金属失效准则和单元删除法模拟钢材的断裂，该准则是通过在材料属性中定义材料的断裂应变、三轴应力、应变率等参数，使金属材料达到断裂应变值后发生断裂，如式(1)[16-17]所示

(1)

式中：C1为纯剪切下的等效塑性应变；C2为单轴拉伸下的等效塑性应变。C1，C2与材料的真实应力、真实应变以及断面收缩率相关。

图3 材料的本构关系Fig.3 Constitutive relationships of materials

1.3 组合梁不同线刚度参数设计

以两跨三柱梁柱子结构为研究对象，重点研究与失效柱相连的双跨梁不同线刚度对结构抗倒塌性能的影响。其中组合梁不同线刚度可分为以下两种情形：①双跨梁的梁高相等，跨度相等(改变跨度)；②双跨梁的梁高相等，跨度相等(改变梁高)。其中以钢梁高度为450 mm，跨度为4 500 mm的试件为标准模型，标准模型的节点剪切板有四排螺栓，钢梁高度每增加(减小)80 mm增加(减小)一排螺栓，以此类推。

1.3.1 情形(1)-改变跨度

在钢梁高度为450 mm的情况下，改变组合梁的跨度，分别取2 700 mm，3 600 mm，4 500 mm，5 400 mm，6 300 mm。试件编号与双跨梁截面高度h、跨度L、高跨比h/L以及梁线刚度k等设计参数，如表1所示，其中梁线刚度计算过程见文献[18]。

表1 情形(1)下结构设计参数Tab.1 Design of structural parameters under case (1)

1.3.2 情形(2)-改变梁高

在组合梁跨度为4 500 mm的情形下，改变钢梁截面高度，分别取290 mm，370 mm，450 mm，530 mm，610 mm。试件编号与双跨梁截面高度、跨度、高跨比以及梁线刚度，如表2所示。

表2 情形(2)下结构设计参数Tab.2 Design of structural parameters under case (2)

1.4 模型验证

为了验证有限元建模方法的正确性，按照1∶3缩尺比例设计了栓焊连接节点组合梁柱子结构试件，并进行了拟静力抗倒塌试验，试验装置如图4所示。其中组合梁跨度取为1 500 mm，边柱长度取1 100 mm，钢梁、钢柱截面的尺寸分别为HM150×100×6×9(mm)、HW150×150×8×10(mm)。混凝土楼板宽度为600 mm，厚度为55 mm。纵向钢筋和分布钢筋分别采用φ10@125和φ6@125，上排纵向钢筋与分布钢筋形成钢筋网。组合楼板与钢梁通过直径为13 mm，长为45 mm的抗剪栓钉连接，栓钉采用双排布置，各个栓钉之间的间距为125 mm，梁柱节点为盖板加强型栓焊连接节点，梁腹板与剪切板采用10.9级M16摩擦型高强度螺栓连接。根据文献[19]中试件的详细尺寸建立了对应的有限元模型，图5为数值分析对栓焊试件破坏现象的模拟结果对比，数值模拟结果与试验断裂过程十分吻合，说明显示动力准静态分析方法可以比较准确的模拟试件断裂位置及断裂后发展路径。

图4 试验加载装置Fig.4 Test setup

图5 有限元模型验证Fig.5 Validation of FE model

试件的数值模型分析结果与试验结果曲线对比，如图6所示。结果表明，两者的荷载位移曲线及内力发展曲线均吻合较好，说明有限元分析模型建模方法具有较好的可靠性，可为后续不同梁线刚度情形下组合梁柱子结构抗倒塌性能研究提供基础。

2 不同梁线刚度影响分析

由于梁端盖板的加强作用，会使得塑性铰发生外移，加强段端部附近位置就会形成塑性铰，从而远离梁柱翼缘交界面，对应截面即为最不利截面。图7所示的截面B1(B4)、B2(B3)为中柱失效工况下的最不利截面。梁端塑性弯矩和最不利截面塑性弯矩关系，如图7所示。

图6 有限元与试验结果对比Fig.6 Comparsion of FE result and test result

图7 梁端塑性弯矩Fig.7 The bending moments of the beam ends

不难看出，当组合梁截面塑性发展完全时，梁端塑性弯矩和最不利截面塑性弯矩存在如下关系(不考虑钢梁局部屈曲的影响)

Mp-=M-+Pdcosθ/2

(2)

Mp+=M++Pdcosθ/2

(3)

dcosθ≈d

(4)

式中：d为最不利截面与相邻柱翼缘的距离，d=dl+10(mm)， 其中dl为盖板长度，本文模型中d取为250 mm；M-为B1(B4)截面塑性负屈服弯矩；M+为B2(B3)截面塑性正屈服弯矩；Mp-为组合梁塑性负屈服弯矩；Mp+为组合梁塑性正屈服弯矩。

根据式(2)～式(6)求得对应塑性阶段组合梁柱子结构失效柱柱顶荷载理论值为Pp，根据式(7)求得梁截面受拉屈服承载力Np，在后文用此进行荷载和轴力的无量纲化计算。各模型的柱顶理论荷载值、梁截面受拉屈服承载力以及全截面塑性屈服弯矩，如表3所示。

ΣM×θ=PΔ，θ=v/l

(5)

(6)

Np=fybAb+fyrAr

(7)

式中：l为梁的净跨；fyb和fyr分别为钢梁和钢筋的屈服强度；Ab和Ar分别为钢梁和钢筋的截面面积。

2.1 荷载-位移曲线

图8给出了组合梁不同线刚度情形下模型的荷载-位移关系曲线，可以看出，不同梁线刚度情形下所有模型的荷载-位移曲线在整个加载过程都出现多次上升和下降，试件破坏过程对应呈现多次间断性破坏特征，且在首次断裂位置处对应结构的峰值荷载。具体表现为，首先与失效柱相连的梁端受拉翼缘发生断裂，随着加载位移不断增大，与边柱节点连接的梁端受拉翼缘发生断裂，直至结构完全失效。

表3 组合梁截面理论值Tab.3 Theoretical value of composite beam’s section

图8 模型荷载-位移曲线Fig.8 Load-displacement curves of models

各模型的荷载-位移关系曲线，纵坐标和横坐标分别通过Pp和θ进行无量纲化。从图8可以看出，随着组合梁线刚度的增大，各模型塑性阶段荷载不断增大。随着位移的增长，模型首次发生断裂并达到峰值荷载。模型首次断裂荷载与理论塑性荷载的对比见表4，可以看到随着组合梁线刚度的增大，首次断裂时对应荷载依次增大，而与塑性荷载理论值的比值依次减小。

2.2 内力发展曲线

不同线刚度情形下组合梁柱子结构的内力发展曲线，如图9和图10所示。对比不同加载位移下截面弯矩与轴力的发展特征可知：①加载前期，各模型的轴力由于压拱效应的存在均为负值，但是数值相差不大。说明不同梁线刚度对此类节点模型的压拱效应影响较小；②根据截面弯矩发展曲线以及表4弯矩对比可以看出，改变双跨梁的梁截面高度，当h/L>1/10时，最不利截面弯矩数值基本接近并逐渐超过全截面塑性极限弯矩，此后稳定在较为稳定的水平，即子结构最不利截面已形成塑性铰；当h/L≤1/10时整个过程的最不利截面弯矩均未达到全截面塑性极限弯矩，说明梁高越大越容易形成塑性铰，受弯破坏特征更为明显；③随着位移的增长，各模型达到首次断裂位移弯矩发生突降并最终转变为负值，此时对应轴力下降但不明显，随后轴力呈现迅速增长的趋势，悬链线机制作用不断显现。

图9 情形(1)下模型内力发展Fig.9 Internal force development of models under case (1)

图10 情形(2)下模型内力发展Fig.10 Internal force development of models under case (2)

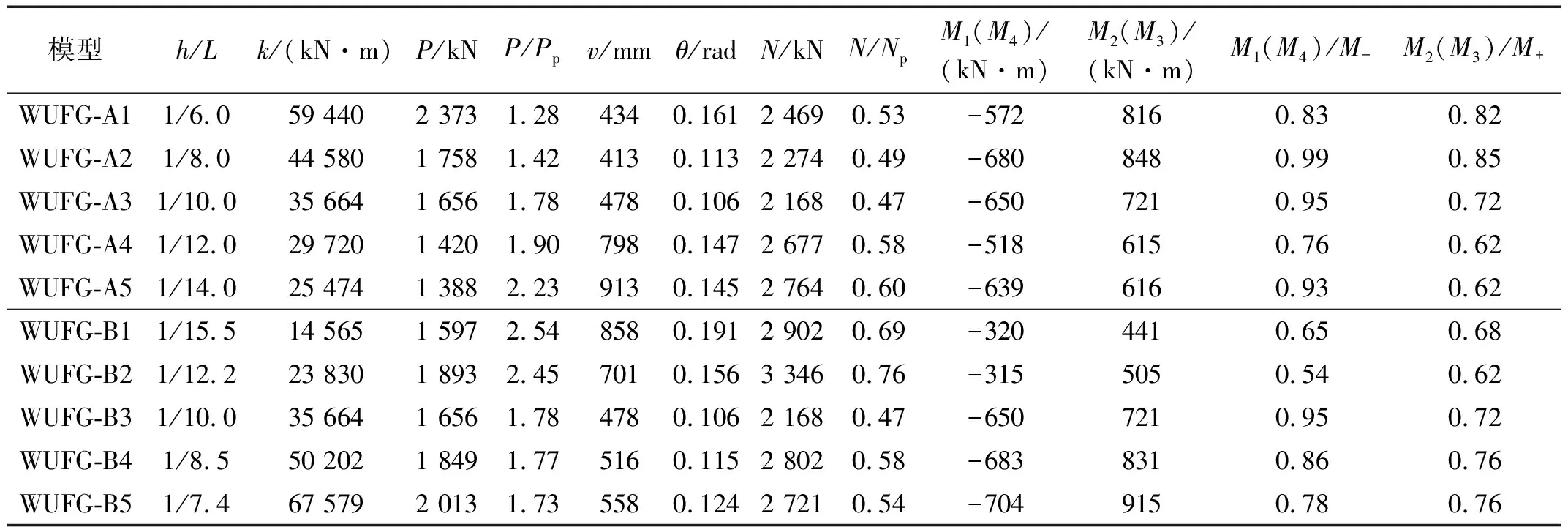
表4 子结构首次断裂点结果Tab.4 Results of assemblies at first fracture point

3 组合梁柱子结构的倒塌失效准则

准确建立合理的结构倒塌失效准则对结构抗力机制贡献定量评估具有至关重要的影响，目前各国学者针对框架结构主要从结构变形和能量两个方面给出了相应的倒塌失效准则，在不同程度上描述了框架结构的倒塌破坏，但是都具有各自的缺陷，内容上表述也不太明确，仍需要进一步完善。

3.1 基于变形的结构失效准则

GSA标准和《建筑结构抗倒塌设计规范》规定当失效柱竖向相对位移超过梁跨的1/5时，可作为结构倒塌的极限位移。但是通过表5分析结果和大量研究结果表明，部分模型当加载位移达到跨度的1/5时，子结构荷载还在峰值荷载附近，后期还具备较为富余的抗倒塌能力储备，说明该倒塌失效准偏于保守。

表5 不同失效准则下组合梁柱子结构的失效位移-荷载Tab.5 Failure displacement-load of composite beam-column assemblies under different failure criterias

3.2 基于能量的结构失效准则

Izzuddin等通过不考虑阻尼有利作用的能量评估模型，可根据结构静力加载条件下的结果近似得到结构在突加竖向荷载下的动力响应。其原理为动力荷载所做的外力功全部转变为结构的内能。根据这一原理可以得到结构的非线性伪静力曲线，这种简化分析方法可以有效的评估结构的非线性动力响应。当伪静力荷载超过最大伪静力荷载点后，其伪静力荷载开始降低，这表明此时会引发组合梁柱子结构的失效，即梁柱子结构吸收的能量不能平衡外部荷载所做的功，具体如式(8)。并且可将基于能量法获得的最大伪静力荷载点作为结构是否发生倒塌判定依据。

(8)

不同组合梁线刚度情形下模型的拟静力曲线，如图11所示。最大伪静力荷载点见表5，根据表5结果可知，基于能量的结构失效准则对高跨比较大的结构是否发生倒塌的判定同样过于保守，不能很好的反映结构失效位移。

图11 模型的动力响应曲线Fig.11 Dynamic response curves of models

3.3 基于抗力机制转换的结构失效准则

结构在外载作用下，其抗力机制发展过程一般经历梁机制阶段、梁机制和悬链线机制混合阶段以及悬链线阶段。其中，梁机制提供抗力在整个倒塌过程中起到积极作用的阶段为主要阶段，该阶段为关键柱失效后结构内力响应的主要阶段，需要重点考察。当梁机制提供抗力对结构抵抗外载开始起不利作用时可认为此时结构失效，对应位移即为结构的极限位移。通过表5可以看出，机制转换准则可以较为准确的找到倒塌失效位移，但要实现这一目标需要进行大量的精细化数值模拟及繁琐的计算分析，故难以应用于实际结构的倒塌分析。

3.4 基于变形的结构失效修正准则

通过已有的倒塌失效准则对比分析可以发现，规范中基于变形的结构失效准则主要是通过控制梁端转角来实现的，对梁线刚度这一关键参数并未充分考虑，显然是不合理的。而基于能量的结构失效准则和抗力转换的失效准则都需要通过复杂的数值计算得到失效位移，不够简单且不具备直观性。由表5可以看出，当梁跨度或者梁高较大时，规范中的失效准则可以较好的预测结构的失效位移，但当梁跨度或者梁高较小时，规范中的失效准则偏于保守，本文通过不同线刚度情形下组合梁柱子结构的倒塌分析结果对规范中基于变形结构倒塌准则进行修正，充分考虑梁高和跨度对结构失效位移的影响，修正后准则如式(9)所示。基于该修正准则得到的失效位移及对应荷载见表5所示，可以看到，该失效准则可以较为简易和准确的预测结构失效位移，具有较好的可操性。

(9)

4 抗力贡献水平

现行的抗倒塌设计规范中仅仅给出简单的基本设计措施和构造要求，关于结构抗力的定量评估方法还亟待补充。为了定量说明以上不同线刚度下梁机制和悬链线机制分别对结构总抗力作出的贡献，基于本文提出的结构倒塌失效准则和图12所示的梁柱子结构力学受力模型，可根据能量等效原则按照下列公式分别计算双跨梁的梁机制和悬链线机制的抗力水平和贡献占比。

PC=2Nsinθ

(10)

PF=P-PC=2Vcosθ

(11)

(12)

(13)

图12 组合梁柱子结构分析模型Fig.12 Analysis diagram of composite beam-column assembly

4.1 情形(1)-改变跨度

图13为情形(1)下双跨梁抗力发展曲线和抗力贡献系数。可以看出，在与失效柱相连的梁端受拉翼缘首次发生断裂前，随着组合梁线刚度的增大，试件的梁机制和悬链线机制提供的抗力都不断增大，说明减小梁的跨度可以有效的提高梁机制和悬链线机制阶段的抗倒塌能力，但是过大的梁线刚度会导致结构过早失效不利于结构的位移发展。

图13 机制抗力分析Fig.13 Analysis of mechanism resistances

随着位移的发展，梁机制抗力不断减小并逐渐由悬链线机制抗力取代，当梁端转角达到0.117～0.220 rad内，悬链线机制成为主导抗力机制抵抗外载，模型的主导抗力机制由梁机制转变为悬链线机制，对应转角随着梁线刚度的增大而不断减小，如图13(c)所示。当结构位移达到极限位移时，此时结构完全由悬链线机制抵抗外载。通过式(12)和式(13)可分别得到双跨梁的梁机制和悬链线机制抗力水平，具体贡献系数如表6所示。可以看到，所有模型的梁机制贡献占比基本都在55%～80%内，悬链线机制贡献占比在20%～45%内，其中梁机制贡献系数随着梁线刚度的减小而不断减小。

表6 情形(1)下抗力贡献系数Tab.6 Resistance contribution coefficients under case (1)

4.2 情形(2)-改变梁高

图14为情形(2)下双跨梁抗力发展曲线和抗力贡献系数。在与失效柱相连的梁端受拉翼缘首次发生断裂前，随着组合梁线刚度的增大，试件的梁机制提供的抗力不断增大，但悬链线机制提供抗力差别不大，说明增加梁高可以有效的提高梁机制阶段的抗倒塌能力，但对悬链线机制抗力的影响并不明显。当梁端转角达到0.118～0.157 rad内，试件的主导抗力机制由梁机制转变为悬链线机制，对应转角随着梁线刚度的增大而不断减小，如图14(c)所示。

图14 机制抗力分析Fig.14 Analysis of mechanism resistances

同理可分别得到双跨梁的梁机制和悬链线机制抗力水平，如表7所示。可以看到，所有试件的梁机制贡献占比基本都在45%～70%内，悬链线贡献机制占比在30%～55%，梁机制抗力贡献系数随着线刚度的增大而不断增大。

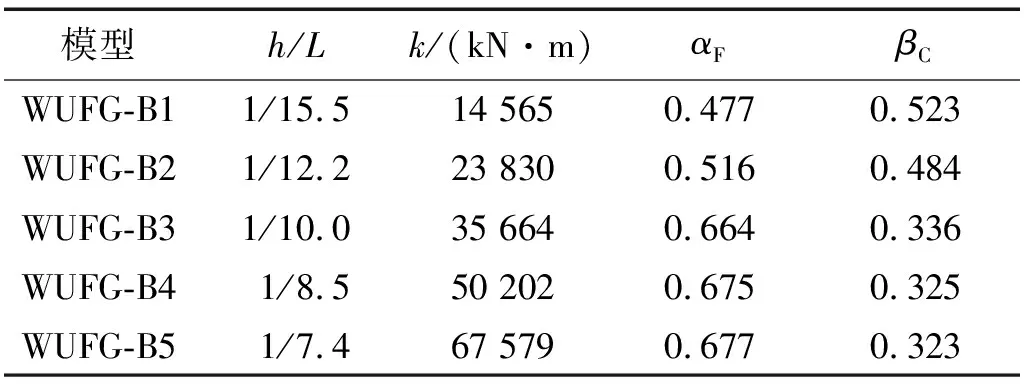
表7 情形(2)下抗力贡献系数Tab.7 Resistance contribution coefficients under case (2)

5 结 论

本文对中柱失效条件下两跨三柱型梁柱子结构的连续倒塌试验结果进行了数值模拟，并基于验证的有限元模型重点研究了双跨梁不同线刚度对组合梁柱子结构性能的影响，具体结论如下：

(1) 所有模型的抗力机制发展过程先后为梁机制阶段、梁机制和悬链线机制混合阶段以及悬链线机制阶段。随着组合梁线刚度的增大，会推后悬链线机制的发挥。并且梁高越大，受弯破坏特征更为明显。

(2) 在大变形阶段之前，结构的梁机制抗力主要受梁线刚度影响，梁线刚度越大梁机制抗力越大。而双跨梁的悬链线机制抗力主要受跨度影响，梁跨度越小悬链线机制抗力越大，梁高对其影响较小。过大的梁线刚度不利于结构的位移发展。整个加载过程梁机制贡献系数随着梁线刚度的增大而增大。

(3) 对目前基于变形的结构失效准则进行了修正，修正后准则可以较为准确得到结构的失效位移，可作为结构发生倒塌破坏的判定依据。利用该准则分别得到了组合梁不同线刚度情形下双跨梁的梁机制和悬链线机制抗力贡献指标，可为结构抗倒塌设计规范的修订提供依据，并对实际工程应用提供一定参考。