基于多分支深度可分离卷积神经网络的滚动轴承故障诊断研究

刘恒畅， 姚德臣， 杨建伟， 张 骄

(1. 北京建筑大学 机电与车辆工程学院，北京 100044；2. 北京建筑大学 城市轨道交通车辆服役性能保障北京市重点实验室，北京 100044；3. 北京市地铁运营有限公司，北京 100044)

目前旋转机械被广泛应用在工厂、飞行器和地面载具，旋转机械的运行状态决定了工程系统的可靠性和安全性，滚动轴承作为旋转机械设备中的重要部件，一旦发生故障会造成严重的经济损失，甚至人员伤亡，滚动轴承故障也是导致机械设备故障的常见原因之一[1]。因此，对于滚动轴承健康状态的监测和诊断极为重要。

在滚动轴承故障诊断中，通常包括：①采集设备振动信号；②对信号进行预处理；③提取信号中有用的特征信息；④建立模型对轴承运行状态进行诊断。但是由于实际旋转机械设备运行时，采集到的振动信号通常包含各种类型混合噪声，如何从信号中提取代表轴承状态的特征信息，辨别不同故障类型和故障程度成为传统轴承故障诊断研究中不可避免的问题[2]。

近几年，深度学习技术的快速发展改变了传统故障诊断方法。深度学习解决了从混合振动信号中提取特征信息的难题，避免了复杂的人工特征提取。较为常用的深度学习方法包括[3]：迁移学习、长短时记忆网络(long short-term memory, LSTM)、深度残差网络(ResNet)。这些方法都能达到较好的诊断精度，但是它们有着同样的问题：模型占据存储空间较大，预测时间长，计算速度慢。这些问题导致深度学习在故障诊断领域的实际应用中较少。

卷积神经网络(convolutional neural network, CNN)是目前深度学习应用最广泛的网络，自从2012年的AlexNet网络提出后，各类CNN模型成为视觉识别竞赛中的优胜者，被证明在图像分类、视觉识别任务中有着优异的性能[4]。相对于传统的浅层神经网络，CNN模型由于卷积层的存在具有权值共享、局部连接等特点，减少了模型的参数量，提高了模型的泛化性，解决了浅层模型在层数加深后经常出现的过拟合问题[5]。Lu等[6]提出将振动信号进行归一化后转换为振动图像，再利用CNN模型对图像进行分类。李恒等提出先对振动信号进行短时傅里叶变换得到包含时域和频域的特征图，在Le-Net5网络的基础上，建立诊断模型，将特征图作为模型输入对轴承运行状态进行诊断[7]。上述方法都能有效诊断轴承运行状态，但是多数研究主要专注于对模型精度的研究，并没有考虑模型预测时间，模型尺寸等问题。

传统CNN模型虽然在各类图像数据集上都表现良好，但是在提高模型精度的同时，模型深度也在加深。例如常见的深度残差网络，层数达到了152层，对运行设备要求较高。为了能够降低模型对设备的内存要求，提高模型在实际应用的预测速度。近年提出了轻量化模型的概念，轻量化模型通过卷积核分解，奇异值分解等方法减少网络参数，提高网络计算速度。常见的轻量化模型包括：SqueezeNet、Xception、MobileNet、ShuffleNet。以上四种模型通过不同方式压缩模型参数，实现网络轻量化。轻量化网络在ImageNet数据集进行试验时，相对于传统CNN模型计算量和参数量都减少了一个数量级，网络精度损失则极少[8]。

试验中利用一维振动信号重构为二维矩阵的思想，将矩阵保存为灰度图作为诊断模型的输入，使用多分支深度可分离卷积神经网络，对滚动轴承故障类型和故障程度进行分类，借助权重剪枝技术对模型进行优化，缩小模型尺寸(诊断模型占运行设备的存储空间大小)，相对于传统深度学习方法提高了诊断效率。

1 理论分析

1.1 技术路线

本文提出的基于多分支深度可分离卷积神经网络的滚动轴承故障诊断方法，利用CNN模型图像分类的功能对轴承故障种类和程度进行诊断。首先需要将采集到的一维振动信号进行标准化，并转换为二维矩阵，将矩阵以灰度图形式保存得到特征样本，分为训练集、验证集和测试集；然后在MBDS-CNN(multi branch depth separable convolutional neural network)模型的基础上建立故障诊断模型；将训练集作为模型的输入，对模型进行训练，通过验证集观察模型在训练过程中诊断精度和损失函数值(loss)的变化，最后将测试集输入到训练好的模型中，对模型性能进行评估获取适合滚动轴承故障诊断的最佳网络架构和超参数。图1为故障诊断方法流程图，图中epoch代表训练集数据的一次遍历。

图1 诊断方法流程图Fig.1 Flow chart of diagnosis method

试验使用多分类交叉熵(categorical cross entropy)作为损失函数,可以准确描述实际输出概率分布与期望分布的距离，损失函数值越小，实际分布与期望分布的差异越小。损失函数公式为

(1)

1.2 振动图像生成

原始振动数据为一维时间序列信号，而CNN模型的输入数据要求是二维矩阵。为了将一维时间序列转换成二维数据矩阵，试验基于时间序列信号，随机选取R个采集点作为转换起始点，连续取样Q个采集点，将Q个采集点转换为N个行向量li，将li进行归一化，每个行向量具有M个采集点。对于N个行向量所构成的M*N二维矩阵P为一个图像样本[9]。R决定了最终得到的图像样本数量，M和N的大小决定图像样本的尺寸，试验中M和N取32，Q取1 024。式(3)是li归一化公式，其中max取1，min取0。图2为数据转化示意图。为了提高图像样本在文中的视觉效果，图3为振动图像样本。

P=[l1,l2,…,lN]T

(2)

(3)

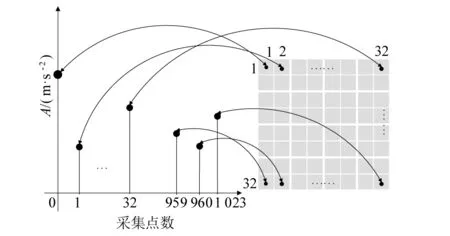
图2 振动信号生成图像样本Fig.2 Image sample generated by vibration signal

图3 振动图像样本Fig.3 Vibration image sample

1.3 深度可分离卷积

传统CNN模型通过卷积层提取图像中的特征，随着卷积层数量的增加，能够抽取到的高阶特征也越多，网络的能力也更加优越[10]。但是层数的增加也使得模型效率降低，对运行硬件的要求也大幅提高。

Xception提出使用深度可分离卷积(depthwise separable convolution)代替传统卷积操作，深度可分离卷积包括两个层：①对每个输入通道使用一个卷积核称为深度卷积(depthwise convolution, DW)；②使用一个1×1的卷积合并DW的输出称为逐点卷积(pointwise convolution, PW)[11-12]。

在标准卷积层，假设输入特征图尺寸为Ni*Ni，通道数为M，卷积核大小为Nf*Nf，卷积核数量为K。则卷积层的计算量为

Ni*Ni*M*K*Nf*Nf

(4)

标准卷积操作包括两个步骤：通过卷积核过滤特征和合并特征产生新的高级特征。深度可分离卷积则将标准卷积的两个步骤分隔开执行，即DW和PW。如图4所示。

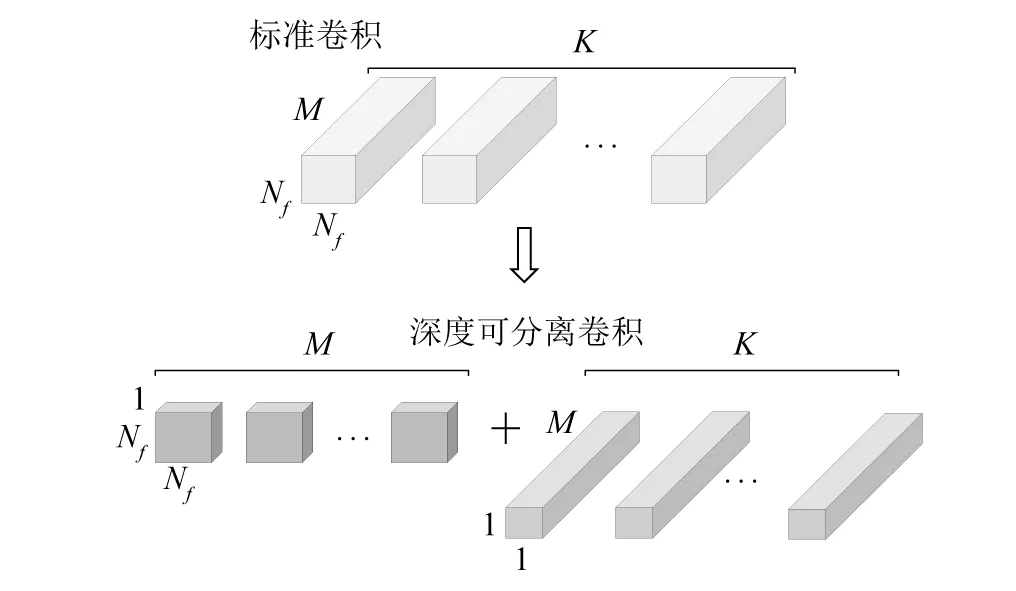
图4 标准卷积与深度可分离卷积Fig.4 Classic convolution and depthwise separable convolution

深度可分离卷积计算量为

Ni*Ni*M*Nf*Nf+K*M*Ni*Ni

(5)

对标准卷积和深度可分离卷积的计算量进行比较

(6)

式中：K为通道数量通常大于1；Nf为卷积核尺寸，常用尺寸包括3×3，5×5，7×7，因此式(5)的值小于1，深度可分离卷积比标准卷积的计算量少。

1.4 权重剪枝技术

由于CNN模型通常具有过参数的特性，使得模型在直接部署时会出现计算成本和内存占用高的问题。因此需要对模型进行权重剪枝，提高网络的效率[13]。

在训练过程中，权重剪枝通过将权重矩阵中最接近0的权重置为0，删除了相对应的神经元连接，减少了模型的浮点运算，提高了模型的稀疏度。随着模型稀疏度的上升，压缩后的模型体积大幅缩小。图5显示了权重剪枝的过程。

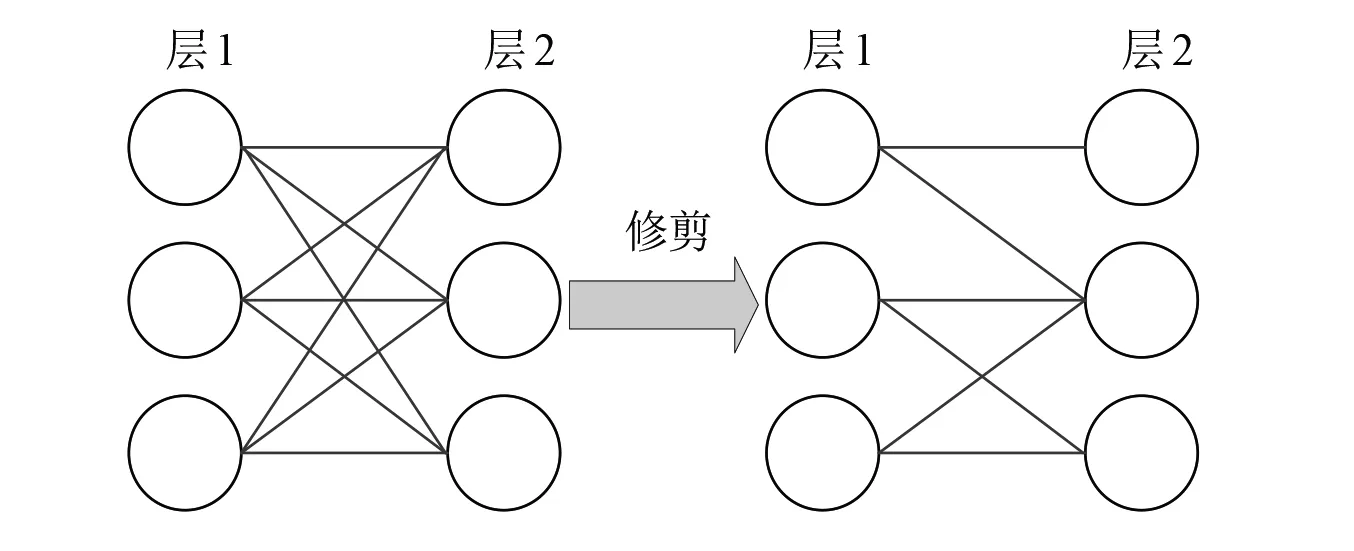
图5 权重剪枝Fig.5 Weight pruning

2 试验验证

2.1 构建数据集

为了验证所提方法的泛化性和抗噪性，在两个轴承数据集上进行了试验，通过在数据集中加入白噪声信号获取具有不同信噪比的带噪信号。式(6)为信噪比(signal noise ratio, SNR)的计算公式。Psignal为信号的有效功率，Pnoise为噪声的有效功率。

(7)

数据集1——由美国西储大学公布的轴承数据构成，试验采用转速为1 730 r/min时驱动端加速度传感器采集到的振动数据，采样频率为12 kHz，使用SKF 6205-2RS深沟球轴承[14]。使用的轴承数据共计10类，正常状态以及内圈、外圈和滚动体故障,故障直径分别为0.18 mm，0.36 mm，0.54 mm。总共建立了6个带噪数据集，信噪比在-6～10 dB，每个带噪数据集包含15 000个样本的训练集、1 000个样本的验证集、10个包含1 000个样本的测试集。

数据集2——为了验证本文所提算法的有效性，设计轴承故障试验台进行验证。试验台如图6所示，由驱动电机、联轴器、齿轮箱和磁粉制动器等组成。在试验台整个运行过程中，采集振动加速度信号，采样频率为12 kHz，转速为1 200 r/min，包含6种轴承状态：正常、内圈故障、外圈故障、滚动体的轻度故障、中度故障、重度故障。试验用的轴承型号为ER16K。建立了6个带噪数据集，信噪比在-2～8 dB，每个带噪数据集包含12 000个样本的训练集、600个样本的验证集、10个包含600个样本的测试集。

试验在Tensorflow的框架下开发，使用AMD的R5-2600x CPU(主频3.6 GHz)，NVIDIA RTX2080ti显卡，主机上安装了CUDA 10.0，Cudnn7.6对显卡运算进行加速。

为了提高数据分类的准确性，数据集中的标签必须全部转换成数字，所以试验中使用独热编码(one-hot)制作标签，独热编码即将不同类别的标签转换为二进制向量，向量维数即故障类别数，在向量中只有一位是1，其余全是0[15]。表1是标签编码表。

图6 轴承故障模拟试验台Fig.6 Bearing failure simulation test bench

表1 标签编码表Tab.1 Label coding table

2.2 建立轴承故障诊断模型

MBDS-CNN使用了1个卷积核3×3的普通卷积，9个深度可分离卷积，1个全局平均池化层和一个全连接层，为了提高模型的表达能力，避免随着层数的加深出现“梯度消失”的情况，MBDS-CNN使用了多分支结构。图7为MBDS-CNN的结构，图中s为卷积步长，c为过滤器数量。

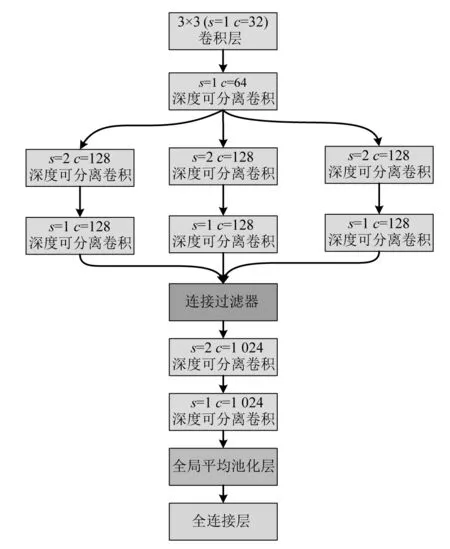
图7 模型结构图Fig.7 Model structure diagram

模型中参数更新的速度由学习率决定，学习率过大，会导致每次更新参数时步长过大，模型无法收敛至极优值，学习率过小，虽然能保证收敛性，但是会降低模型收敛的效率。

为了避免以上所述问题导致模型无法达到最佳性能运行的情况。试验中使用自适应学习率，提高模型优化速度，学习率初始值设置为0.001，在训练过程中，每个epoch结束后，在验证集上评估当前模型loss和精度，每隔一个epoch检测loss值的变化，小于0.000 1时，学习率进行衰减，衰减公式为

lr*=lr*0.1

(8)

为了进一步加快模型的收敛速度，模型使用RMSprop算法对使用损失函数进行优化，避免了优化过程中幅度过大的问题。

2.3 诊断结果

研究采用了MobileNet、Vgg16、LeNet5、ResNet和AlexNet模型作为对比组试验，使用相同的数据集与所提方法进行比较。在10个测试集上对模型效果进行评估，计算出模型的平均精度和标准差。

表2为MBDS-CNN模型与对比试验在数据集1(无白噪声)上的平均精度、标准差、预测时间和模型尺寸。可以看出在无白噪声的情况下各模型都具有良好的诊断效果，MBDS-CNN在精度上并无优势，但是在预测时间和模型尺寸上，MBDS-CNN模型具有卓越的性能。与同为轻量化模型的MobileNet相比，MBDS-CNN的模型尺寸仅为MobileNet的5.2%，预测时间也比MobileNet快了0.22 s。

表2 数据集1(无白噪声)上不同模型试验效果Tab.2 Experimental results of different models on dataset 1 (without white noise)

为了验证MBDS-CNN模型的鲁棒性，在数据集1上加入了不同强度的噪声，表3和表4分别显示了各模型在多种噪声环境下的平均诊断精度和标准差。

由表3和表4可以看出，在数据集1 的信噪比在5～10 dB时，各模型诊断效果基本相同，但是当信噪比低于0时，对比试验模型出现诊断错误的现象，尤其当信噪比在-6 dB时，只有MBDS-CNN的诊断精度依然保持在90%以上。这是因为在信噪比较低的情况下，故障特征信息容易被噪声信号淹没，MBDS-CNN的多分支结构保证了其可以提取更丰富的特征，融合不同分支上提取的故障特征信息。

表3 数据集1上不同模型的平均诊断精度Tab.3 Average accuracy of different models on dataset 1

表4 模型诊断精度的标准差(数据集1)Tab.4 Standard deviation of model diagnosis accuracy(dataset 1)

图8通过t-SNE算法[16]显示了数据集1信噪比为-6 dB时，各模型的预测结果。使用阿拉伯数字0～9表示轴承的健康状态。可以看出图8(a) MBDS-CNN的分类效果明显强于其他模型。

表5为MBDS-CNN模型与对比试验在数据集2(无白噪声)上的平均精度、标准差、预测时间和模型尺寸。与数据集1上各模型的表现相同，在无白噪声的情况下，各模型都具有良好的诊断效果。

表6和表7显示了在数据集2上不同模型的平均诊断精度。可以看出MBDS-CNN在数据集2上依然具有良好的抗噪性。与在数据集1上的表现相似，对比模型在信噪比为0时，出现诊断精度损失的现象。MBDS-CNN在信噪比为-2 dB时，诊断精度下降，但是其诊断效果依然为各模型中最佳的。

试验结果显示MBDS-CNN在数据集1信噪比为-6 dB，数据集2信噪比为-2 dB时，能够更好的观测出模型在抗噪性上的优越性。图9为不同模型在低信噪比数据集上训练时loss值优化的过程(因AlexNet在低信噪比情况下，模型未收敛，所以图中未显示)。

图8 数据集1(SNR=-6 dB)上不同模型预测分布Fig.8 Prediction distribution of different models on dataset 1 (SNR=-6 dB)

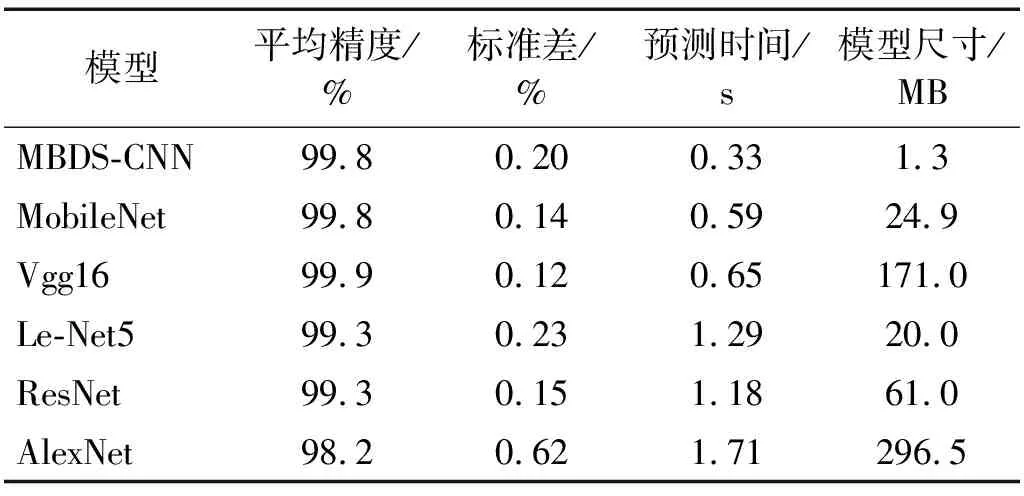
表5 数据集2(无白噪声)上不同模型试验效果Tab.5 Experimental results of different models on dataset 2 (without white noise)

表6 数据集2上不同模型的平均精度Tab.6 Average accuracy of different models on dataset 2

表7 模型诊断精度的标准差(数据集2)Tab.7 Standard deviation of model diagnosis accuracy (dataset 2)

图9 不同模型在低信噪比数据集上的训练过程Fig.9 Training process of different models on low SNR dataset

由图9可以看出在两个数据集上，MBDS-CNN的收敛速度和收敛效果都是最佳的。部分模型虽然在收敛效果上与MBDS-CNN相似，但是却出现了过拟合现象，导致模型在测试集上的诊断效果较差，如图9(a)中的MobileNet与图9(b)中的Le-Net5。

为了进一步观测各模型对不同故障类型的诊断效果，利用混淆矩阵对各模型在数据集2(SNR=0)上的分类结果进行可视化。如图10所示，除图最右列和最底行的方块，对角线的方块显示了诊断正确的样本数量，其他方块显示了诊断错误的样本数量，方块中的百分比代表了当前块样本数量占总体样本数量的比例。矩阵右下角的方块显示了模型的精度。最右列的方块代表了输出类的精度，最后一行代表了召回率。

由图10可以看出MBDS-CNN对不同故障类型都具有良好的诊断效果。其余模型会出现对某一故障类型诊断效果差的现象，例如Vgg16模型无法有效的对滚动体重度故障和外圈故障进行诊断，诊断精度仅为84%和86%。ResNet模型对多数故障类型都能精准分类，但是在诊断外圈故障时也出现了诊断错误的现象，对外圈故障的诊断精度仅为83%。

图10 数据集2(SNR=0)上分类结果可视化Fig.10 Visualization of classification results on dataset 2 (SNR=0)

从以上试验结果可以看出常见的CNN模型在信噪比高的情况下具有良好的诊断效果，但是在噪声增强的情况下，诊断精度会出现较大的损失。另一方面，经典CNN模型具有模型尺寸大，预测时间长的缺点。MBDS-CNN使用深度可分离卷积和多分枝结构在缩减模型尺寸的同时，保证了模型的诊断精度，可以在噪声环境下对不同故障类型和故障程度进行分类。

3 结 论

本文针对基于传统CNN的故障诊断方法具有模型尺寸大，诊断速度低，难以区分不同故障程度的缺点。提出基于多分支深度可分离卷积神经网络的轴承故障诊断方法。通过本文试验，验证了：

(1) 将振动信号转换为灰度图作为MBDS-CNN模型的输入，能够很好的发挥CNN在图像分类上的优势。

(2) 使用深度可分离卷积和权重剪枝技术可以大幅压缩模型尺寸，另一方面，多分支结构保证了模型压缩后的诊断精度。

(3) MBDS-CNN相对于传统CNN模型，具有更好的抗噪性，更快的诊断速度和更小的模型尺寸。

试验结果表明本文提出的基于多分支深度可分离卷积神经网络的滚动轴承故障诊断方法能较好地辨识轴承不同故障类型以及故障程度，为深度学习在故障诊断领域的应用提供了新的思路。