基于双结构深度学习的滚动轴承故障智能诊断
齐咏生, 郭春雨, 师 芳, 高胜利, 李永亭
(1. 内蒙古工业大学 电力学院,呼和浩特 010080; 2. 内蒙古自治区机电控制重点实验室,呼和浩特 010051;3. 内蒙古北方龙源风力发电有限责任公司,呼和浩特 010050)
滚动轴承是旋转机械的重要部位,其工作状态的好坏直接影响整个设备的工作性能,且轴承运行环境复杂,极易发生故障,而轴承故障往往会造成更为严重的事故。因此,对滚动轴承进行准确的故障识别与分类是工程应用中至关重要的问题,从而最大限度的发挥轴承的工作潜力,节约开支。
当前,工业生产快速发展,轴承故障频发,轴承故障呈现出一种“大数据”的特性,使得BP神经网络等浅层模型面临维数灾难等问题,进而造成现场获取的大量数据得不到有效利用,且传统特征提取与选择的方法具有一定的复杂性和不确定性。而以卷积神经网络(convolutional neural network,CNN)和深度置信网络(deep belief network,DBN)为代表的深度网络提供了一种能够自动提取原始数据特征的有效方法,可以解决数据量大、特征提取困难等问题。
目前,采用CNN与DBN方法实现故障识别与诊断还处于初级研究阶段。Hoang等[1]提出了一种基于卷积神经网络深层结构的轴承故障诊断方法。该方法直接以振动信号转化为振幅图作为输入数据,不需要任何特征提取技术,在噪声环境下具有较高的精度和鲁棒性。Wen等[2]提出一种新的基于CNN的数据驱动故障诊断方法,它通过将信号分割后重新排列转换为二维矩阵再利用CNN来提取故障特征。Lu等[3]提出了一种基于有监督深度学习的轴承数据特征表示方法,利用逐层贪婪训练的传递规则,建立了一种鲁棒的深层层次结构训练方法。结果表明CNN模型可以有效性的对滚动轴承故障进行分类。
陶洁等[4]提出基于细菌觅食决策和深度置信网络的滚动轴承故障诊断方法,利用采集的故障数据对深度置信网络进行训练,以构造细菌觅食决策算法的适应度函数,通过计算各个细菌的适应度来衡量模型的优劣,提高滚动轴承故障诊断的准确率。Shao等[5]提出了一种用于滚动轴承故障诊断的优化深度置信网络,对基于能量函数的受限玻尔兹曼机(restricted Boltzmann machines, RBMS)预训练后,采用随机梯度下降法对所有连接权值进行微调,提高了DBN的分类精度和鲁棒性。Tamilselvan等[6]采用小波包变换提取具有代表性的故障特征,并引入深度置信网络实现故障类型细节特征提取。更多学者[7-11]利用DBN在滚动轴承故障诊断、状态监测、退化性评估等领域展开研究,取得了比传统模式识别更好的分类效果。上述研究也表明,DBN的一个显著特点是可直接从低层原始信号出发,通过逐层贪婪学习得到高层特征表示[12],可有效提取微小故障的敏感特征,避免特征提取与选择的人工操作,消除传统人工特征提取与选择所带来的复杂性和不确定性[13-14]。
综上,采用深度学习进行特征提取仍是一种行之有效的方法,本文也延续了这样的思路。然而,上述研究中,均未考虑故障样本不完备和无标签的情况,而这样的情况往往在实际生产中是普遍存在和不可避免的。
当前常用的轴承故障诊断算法,大部分建立在故障库完备且样本充分的条件下。但在实际应用中,常常无法获取多类别的样本或者获取多类别样本的代价极高,造成各类样本数严重不平衡,且大量样本数据是无标签的,使得传统的模式识别方法很难应用或效果不佳。如上所述,深度网络具有很好的特征提取能力,但不具备自主学习能力,因此,单凭深度网络无法实现新类别的学习,必须结合其他方法完成无监督或半监督的自学习过程。Chopra等[15]提出一种基于训练集数据寻找相似度度量的方法,其思想是学习一个将输入数据映射到目标空间的函数,该函数使目标空间中同类别的数据聚合,不同类别的数据分离。借鉴该思想,本文引入一种两输入结构,并采用相似度进行度量,提出了基于相似度度量和CNN结合的半监督学习网络,以此来解决故障类型自学习的问题。即对于未经训练的新故障、新类别,在目标空间中使其与已知类别或故障快速分离,与同种类别或故障快速聚合,最终产生新故障或新类别。
另一方面,故障损伤等级的判别也是一个重要问题,它直接决定了设备工作计划调整和备品配件储备问题,是工业生产最为关心的问题。依托DBN网络对信号的微弱差异更为敏感的特性,本文将DBN和贝叶斯分类器相结合,提出了基于DBN与贝叶斯分类器的故障损伤等级半监督学习网络,实现故障损伤等级的识别与自学习问题。
综上,本文提出了基于深度学习的双结构网络,用于滚动轴承故障类型自主学习和故障损伤等级自动识别算法。在不完备数据建模的情况下,建立故障类型和损伤等级的识别网络。最后,以轴承故障平台数据为例,验证双结构自学习模型的有效性。
1 故障类型自学习模型
1.1 基于相似性度量的机器学习模型
在大型滚动轴承的故障信息中,难以获得大量有标签的数据信息。需要从有限的有标签数据中学习特征,去识别大量的无标签数据。相似性度量可以解决上述问题。
基于能量的相似性度量模型,如图1所示,其中x1和x2是一对输入机器学习模型的图像。Y是一个二进制标签(非1即0),当x1和x2属于相同类时Y=0(相同对);当x1和x2属于不同类时Y=1(不同对)。Gw(x)为样本进入CNN的输出,样本x1和x2通过网络映射成低维空间两点Gw(x1)和Gw(x2)。Ew(x1,x2)可以被看作一个“能量”函数,用其来度量x1和x2之间的相似性,具体定义为
Ew(x1,x2)=‖Gw(x1)-Gw(x2)‖
(1)
式中,Gw(x)为样本x进入CNN中的卷积层和全连接层,后展开成的一维的特征向量。
定义图像属于相同对表示为(x1,x2),不同对表示为(x1,x′2),机器学习模型可以运行的必要条件如下: ∃e>0,使得Ew(x1,x2)+e 图1 机器学习模型Fig.1 Machine learning model 训练模型时定义如下的损失函数,该函数的大小只与输入样本和网络参数有关。 (2) J(w,(Y,x1,x2)i)= (3) (4) 当求函数f关于参数w的最小值时,这个条件确保了模型所得到的解满足条件1所在的区域。 对于f的极小值位于无穷远处,则要满足以下条件。 当满足以上条件时,通过最小化损失函数模型会得到参数w,既模型可以学习到相同样本的共性特征,不同样本的差异性特征。 CNN不具备无监督学习能力,单凭CNN网络无法实现类别的无监督学习,而将相似性度量与CNN结合可实现对新类别的识别与自学习。 如图2(a)所示为CNN与相似性度量相结合的故障自学习模型的总体算法示意图。该算法使用不完备的数据建模:首先,对振动信号做形态学滤波,增强信号的脉冲特征,同时抑制部分噪声。之后对滤波后数据进行S变换得到时频图,这里采用S变换的时频图更易于提取同类型不同损伤程度的共性特征(3.2节给出验证结果)。将时频图输入CNN,之后将其映射到目标空间(本文采用二维空间),并利用双输入的相似性度量对相同类型故障聚合,不同类型故障分离。接下来利用目标空间的坐标值计算输入数据的质心和最小聚类半径(Rmin),其中Rmin的计算采用DBSCAN(density-based spatial clustering of applications with noise)[16]来确定。最后,以训练集的质心坐标为中心,计算训练集与测试集质心之间的欧式距离,若此距离小于Rmin,则属于该训练集类型;以此类推,当该距离均不小于所有已知类型的Rmin,则该测试集为新类型,即属于新故障类别,由此可实现故障类型的自增长和自学习。算法具体步骤如下: 步骤1假设有一种未知故障类型X和若干已知故障类型Xi(i≥2),将所有原始振动信号进行数学形态学滤波,去除部分背景噪声,对数据按照每组M个采样点进行分割(本例中选取M=1 200)作为输入样本;之后每组数`据均进行S变换[17-18]处理得到每组振动数据对应的时频图,然后把时频图转换成n×n的矩阵(本例中n=128)。取所有信号数据的80%作为训练集数据,20%作为测试集数据。 步骤2建立相似性度量与CNN相结合的网络结构。本文采用的CNN架构如下:选取五层卷积网络,第一层16个卷积核,第二层32个卷积核,第三层64个卷积核,第四层128个卷积核,第五层256个卷积核,卷积核大小为5×5。优化算法选取Adam,Adam对超参数(学习率、正则化系数等),最大训练次数为4 000次。网络训练如下:每次任取训练集中两个故障样本(时频图)输入CNN,输出分别为Gw(x1),Gw(x2),依据式(1)~式(3)分别计算Ew(x1,x2)、总能量函数ξ(w)和损失函数J,之后采用优化算法Adam对ξ(w)中的w进行寻优,使损失函数J最小,重复上述过程,最终完成网络训练。 步骤3网络训练好后,把训练集已知故障类型的时频图输入CNN,每种故障振动信号的时频图通过CNN最后一层都会得到一个映射到目标空间的坐标值(x,y),由1.1节双输入相似性度量结构的原理可知,同一类型故障会在目标空间越来越近,而不同类型故障则越来越远。最终,两类不同类型故障会在目标空间汇聚成各自不重合的两簇,完成网络对不同特征的学习过程。计算训练集每种类型故障在目标空间集合的质心,第i类在目标空间的质心记为TrainCi。 步骤4每一类在目标空间的最小聚类半径Rmin是一个非常重要的参数,它直接影响到分类与故障自增长结果的好坏。根据DBSCAN的散点图确定半径Rmin的值。 步骤5将测试集数据通过CNN映射到目标空间,得到测试集在目标空间坐标,计算测试集质心记为TestC。求测试集的TestC与训练集中TrainCi之间的欧式距离,当TestC与第i类故障的TrainCi之间的距离小于Rmin,则判定测试集中未知故障属于训练集中第i类故障类型;当TestC与训练集中所有的TrainCi之间的距离都不小于Rmin,则判定测试集中未知故障属于新故障类型,从而实现故障类型的分类与自学习过程。 完成滚动轴承故障型类识别后,将已知故障类型的样本数据导入下一级网络模型,作为故障损伤等级模型的输入。 贝叶斯分类器的分类原理是通过某对象的先验概率, 利用贝叶斯公式计算其后验概率,即该对象属于某一类的概率[19],多变量正态分布的概率密度函数为 (5) 式中:x为n维向量;mi为n维均值向量;ci为协方差矩阵,后验概率可表示为 (6) 式中:P(wi)为先验概率,即后验概率=概率密度函数×先验概率/证据因子。若此时有两组n维向量x1和x2,对它们划分训练集与测试集,通过训练集进行训练后,便可得到x1的测试集属于x1的概率P1和x1的测试集属于x2的概率P2,且P1+P2=1,如果P1与P2之间相差较大,则认为x1和x2是有很大差别的数据,判定它们属于不同类别;如果P1与P2之间相差较小,则认为x1和x2是很相似的数据,则判定属于相同类别,进而可实现损伤等级的细分。 由于对故障数据做S变换处理后,更容易发现不同故障损伤等级之间的共性,而要实现故障损伤等级的分类则需要利用他们之间的差异性。因此,在此网络中不需要进行数据的S变换,而直接将已判定故障类型的原始数据归一化处理后作为DBN的输入。 图2(b)即为DBN自学习模型的算法总体示意图。该算法的核心思想为:假设现有一种未知故障损伤等级和若干已知故障损伤等级,将归一化处理后的各个损伤等级的信号作为DBN的输入进行特征提取,并把DBN提取特征作为贝叶斯分类器输入,通过贝叶斯判定规则将各已知故障损伤等级与未知故障损伤等级的信号进行两两分类,进行逐一判定。具体识别步骤如下: 步骤1建立DBN特征提取网络,通过试凑法确定DBN网络结构,本例中选取DBN输入层节点为500,确定隐层数为4、各隐层节点为600-300-100-3、各RBM学习率为0.1、最大预训练迭代次数设为100时提取的特征分类效果最好。 步骤2对每种故障损伤等级的信号分割为R个采样点的样本,并进行归一化处理,将处理完的各个信号均转化成一个u行v列的矩阵,其中u×v=R。这样,每种故障信号在DBN最后一层隐层神经元中都会得到一个u行3列的特征矩阵,并把每种故障种类的特征矩阵的前u1行作为贝叶斯判定网络的训练集,剩下的u2行作为贝叶斯判定网络的测试集,即u1+u2=u。 步骤3逐一的将未知种类X′与各已知种类Xi分别进行两两分类,每次分类都选取未知种类与已知种类Xi的训练集对贝叶斯分类器进行训练,通过训练好的贝叶斯分类器对测试集进行判定。 步骤4对贝叶斯分类器,将已知种类Xi和未知种类X′在DBN中提取的特征矩阵分别记为m和m′,每组特征又划分为训练集为m1和m′1,测试集为m2和m′2,即m1+m2=m,m′1+m′2=m′。首先,假设贝叶斯分类器的先验概率pw1和pw2均为0.5,其中pw1为待测数据集属于已知种类的先验概率,pw2为待测数据集属于未知种类的先验概率;其次,通过训练集m1计算出均值mean1和协方差cov1矩阵,并通过训练集m′1计算出均值mean2和协方差cov2矩阵,再将测试集m2或m′2分别代入式(7)和式(8)求取概率密度函数S1和S2,从而根据式(9)计算出证据因子。 图2 算法总体框图Fig.2 Algorithm overall block diagram (7) (8) S=pw1×S1+pw2×S2 (9) (10) (11) 最后,根据式(10)和式(11),分别计算后验概率P1和P2,其中P1代表m2或m′2属于已知种类的概率,P2代表m2或m′2属于未知种类的概率,且P1+P2=1。定义当∂1≤|P1-P2|≤1时,则判定未知种类与已知种类之间存在较大的差异性,即未知种类与已知种类属于不同的故障等级,当P1>P2时,判定m2或m′2属于已知种类;当P1 为表明本文算法的有效性,采用西储大学轴承故障实验平台采集数据进行算法验证,实验平台如图4所示,该实验针对一台1.471 kW的电机轴承,其型号为6205-2RS JEM SKF。通过电火花加工技术,分别在轴承的滚动体、内圈和外圈上布置了单点故障,故障损伤等级包括0.177 8 mm,0.355 6 mm和0.533 4 mm,经电动机驱动端的轴承座上放置的加速度传感器来采集故障轴承的振动加速度信号,采样频率为12 kHz,实验数据如表1所示。 图3 总体算法流程图Fig.3 Flow chart of overall algorithm 图4 轴承试验装置Fig.4 Bearings test device 表1 西储大学轴承故障数据Tab.1 Bearing fault data of Weastern Reserve University 3.2.1 故障类型自学习 首先定义grade1、grade2和grade 3分别代表损伤尺寸为0.177 8 mm,0.355 6 mm和0.533 4 mm的滚动轴承故障。采用大写字母N、I、O和B分别代表正常、内圈故障、外圈故障和滚珠故障类型,如Igrade1代表损伤程度0.177 8 mm的内圈轴承故障,后续表达与此相似,不再赘述。验证故障类型自学习时,构造数据集如下:使用不完备数据训练,每组实验任意选取两种故障作为已知种类,并在每组中设计不同实验,每次实验任选一种故障作为未知故障,通过判定结果确定该故障属于已知故障还是属于未知故障新类型。表2给出了各组及各实验所选故障种类组合。 故障类型自学习模型对数据预处理结果分析如下:如图5所示,为3种原始故障数据做S变换后得到的时频图。由图5可知,同种故障类型信号经S变换后频谱图之间存在相似性,但可以发现内圈(见图5(d))和外圈(见图5(f))的时频图中脉冲波形有相似性,显然对后面的分类识别会造成一定的误判。为解决这一问题,我们在S变换之前添加了形态学滤波,去除部分噪声的干扰。由图6可以看出,形态学滤波之后再做S变换得到频谱图,同种故障有较强的相似性,不同故障具有较大的差异性。由此也证明,预处理环节,在S变换前增加形态学滤波的必要性。 表2 故障类型分类自增长实验分组Tab.2 Experiment groups of self-growth for fault type classification 图5 原始信号做S变换得到的时频图Fig.5 The time-frequency diagram of the original signal by S-transformation 接下来以组1的实验1~实验6的分类结果(已知种类为B grade1和I grade2的实验)为例进行分析,其在目标空间分类结果如图7所示。图7(a)表示测试集为B grade1和I grade2在最后一层网络的输出,图中左上角为B grade1在目标空间所处的位置,右下角为I grade2的位置,可以看出CNN具有对同类故障汇聚不同类故障分离的特性。图7(a)中均为对故障数据用上文提到的预处理方法后得到的频谱图,为了更方便识别,我们用数字来代替各个故障的时频图,其中数字“2”代表B grade1,数字“3”代表I grade2。 图6 形态学滤波后做S变换得到的时频图Fig.6 Time frequency diagram obtained by S transformation after morphological filtering 为了使各个故障在目标空间有参照物,更好的体现出在目标空间汇聚和分离特性。我们同时将测试集B grade1,I grade2和B grade3映射到目标空间其结果,如图7(b)所示,图中数字“5”代表B grade3。图中可以明显看出“2”和“5”在目标空间汇聚,说明B grade1和B grade3为同一类型故障,在时频图中有较强的相似性,两个样本融合到目标空间的右上角。同时将测试集B grade1,I grade2和I grade3映射到目标空间其结果如图7(c),图中数字“4”代表I grade3。与图7(b)相似,由于I grade2和I grade3为同一类型故障,所以“3”和“4”融合到目标空间的右下角。通过以上实例,可以表明故障类型对未学习过的不同损伤程度的同类型故障有较强的辨识能力。 图7 部分故障映射到目标空间的结果示意图Fig.7 The result of each fault mapping to the target space 同时将测试集B grade1,I grade2和O grade1在目标空间进行输出,其结果如图7(d)所示,图中数字“1”代表O grade1。可以看出,图中共形成了3簇集合,即由于B grade1,I grade2和O grade1在时频图中没有相似性,所以它们映射到目标空间之后各自形成一簇。由图可知CNN对未学习过的不同类型未知故障也具有很好的辨识能力。 将训练集在目标空间的映射结果进行解析,计算输入数据的质心和最小聚类半径(Rmin)。在目标空间输入数据质心的定义为 (12) 将目标空间中的输入数据代入式(12),这里我们不妨假设各点的质量均为m,即mk=m(k=1,…,n),最后可求出该类数据在目标空间的质心。 最小聚类半径(Rmin)是根据DBSCAN中的散点图进行定义和确定的,定义和计算过程如下: (1) 计算每个点的k-距离值,并对所有点的k-距离集合进行升序排序,输出的排序后的k-距离值。DBSCAN聚类中k-距离的定义是:给定数据集P={p(i);i=0,1,…,n},对于任意点P(i),计算点P(i)到集合H的子集S={p(1),p(2),…,p(i-1),p(i),p(i+1),…,p(n)}中所有点之间的距离,距离按照从小到大的顺序排序,假设排序后的距离集合为H={d(1),d(2),…,d(k-1),d(k),d(k+1),…,d(n)},则d(k)就被称为k-距离。 (2)根据所有点的k-距离集合H,拟合出一条排序后的H集合中k-距离的变化散点图。绘制曲线,确定半径(Es)的值。 (3) 根据最小包含点数定(Pmin,我们选取Pmin=6)和Es。选择不同的Es,使用散点图对比聚类效果,最后确定Es。最终确定的Es即为最小聚类半径(Rmin)。 计算出训练集与测试集中各个质心之间的欧式距离(D)。训练集与测试集中各个质心的坐标与距离,如表3所示。根据判别规则(如果测试集中的未知故障与训练集中已知故障类型的第i类类型故障的距离Dit 表3 质心坐标在目标空间的距离及分类结果Tab.3 The classification results and distance of centroid coordinates in target space 3.2.2 故障损伤等级自学习 验证故障损伤等级自学习时,通过多次实验验证,我们确定贝叶斯判定方法中∂1=0.6,∂2=0.3。计算分类准确率时采用如下公式 (13) 式中:n为分类错误的点;N为总的分类点个数。 (1) 两种故障损伤等级分类自增长。 为实现每种故障类型下不同故障损伤等级的分类学习,设计测试实验如表4所示。在每种故障类型下均选取一种等级作为已知损伤等级,不妨设每种故障下grade1为已知等级,其它损伤等级为测试等级,当判定结果成立时认为两种损伤等级相似,否则认为是一种新的损伤等级。不同损伤等级下,采用的维修策略不同,如轻微损伤等级下,只需进一步观察或调整运行计划;而严重损伤等级下则必须停机更换,否则会造成更为严重的事故。 如图8~图10所示,为表5中实验1~实验3的分类结果。图8中网络实际输出代表I grade1与I grade2的分类结果,图中前20个点为已知损伤等级(I grade1),后20个点为未知损伤等级(I grade1)。本级分类器只能判断已知损伤等级与未知损伤等级是否为同一等级(当40个点在同一直线上时,为相同类型;当40个点不在同一直线上时,为不同类型),进而判断未知故障为已知损伤等级还是新的损伤等级(以下类同,不再赘述)。可以看出,只有实验2将已知和未知两种故障损伤等级的测试样本分到一类中,表明未知样本与已知样本同属于一类损伤等级。根据式(12)可算出分类准确率为95%。 表4 两种故障损伤等级分类实验分组Tab.4 Experiment groups of classification with two fault levels mm 图8 未知故障等级为0.355 6 mm的内圈故障分类结果Fig.8 Results of fault level classification with unknown fault level of the inner ring is 0.355 6 mm 图9 未知故障等级为0.177 8 mm的内圈故障分类结果Fig.9 Result of fault level classification with unknown fault level of inner ring is 0.177 8 mm 图10 未知故障等级为0.533 4 mm的内圈故障分类结果Fig.10 Results of fault level classification with unknown fault level of the inner ring is 0.533 4 mm 将表4的所有实验结果列于表5中。由表5可知,各个实验的分类准确率均达到90%以上,表明本文方法能够实现两种故障损伤等级的自学习和自增长分类,验证了该故障损伤等级判定网络的有效性。 表5 两种故障等级自增长实验结果Tab.5 Classification results for two fault levels (2) 三种故障损伤等级分类自增长。 当已知两种故障损伤等级的条件下,实现第三种故障损伤等级的自学习和等级自增长。为此,构造测试实验如表6所示,其中实验1~实验3的分类结果分别如图11~图13所示。 表6 三种故障损伤等级分类实验分组Tab.6 Experiment groups of classification with three fault level mm 如图11所示,网络实际输出1、网络实际输出2分别代表grade3和grade1以及grade3和grade2的分类结果,其中未知故障损伤等级为grade3,而grade1和grade2为已知故障损伤等级。可以看出,未知损伤等级为grade3(0.533 4 mm)外圈故障时,与grade1(0.177 8 mm)和grade2(0.355 6 mm)均不同类,可以判定grade3属于一种新的故障损伤等级。由式(13)可计算分类准确率分别为95%和100%。图12和图13给出了相似的结果,测试样本均正确的分类到相同的损伤等级中,分类准确率分别为95%和90%。 图11 未知损伤等级为0.533 4 mm外圈故障分类结果Fig.11 Results of fault level classification with unknown fault level of the outer ring is 0.533 4 mm 图12 未知损伤等级为0.355 6 mm外圈故障分类结果Fig.12 Results of fault level classification with unknown fault level of the outer ring is 0.355 6 mm 图13 未知损伤等级为0.177 8 mm外圈故障分类结果Fig.13 Results of fault level classification with unknown fault level of the outer ring is 0.177 8 mm 将表6的所有实验结果列于表7中。由表7可知,各个实验的分类准确率均达到85%以上,表明本文方法能够进一步实现三种故障损伤等级的自学习,也间接表明当损伤程度进一步增加时,本文方法能够继续进行分类的自增长,体现出一定的学习智能性。 表7 三种损伤等级分类结果汇总Fig.7 Summary of classification results for two fault levels 本文针对当前工业生产中“数据丰富,信息匮乏”,传统模式识别的方法很难建立有效的诊断模型这一问题,提出了基于深度学习双结构的滚动轴承轴承故障类型与损伤等级的自学习方法,该方法通过建立相似性度量与CNN结合网络构建故障类型自学习模型;其次建立DBN特征提取和贝叶斯分类器构建故障损伤等级自学习模型,对完成故障类型分类的故障数据进一步实现故障损伤等级分类的自增长。最后采用西储大学的轴承故障实验平台对本文提出算法进行验证,表明了该算法的有效性和实用性,对于解决当前工业生产中的数据自学习问题给出一定的解决方案,具有较好的实用价值。
(1-Y)JX(Ew(x1,x2)i)+YJB(Ew(x1,x2)i)



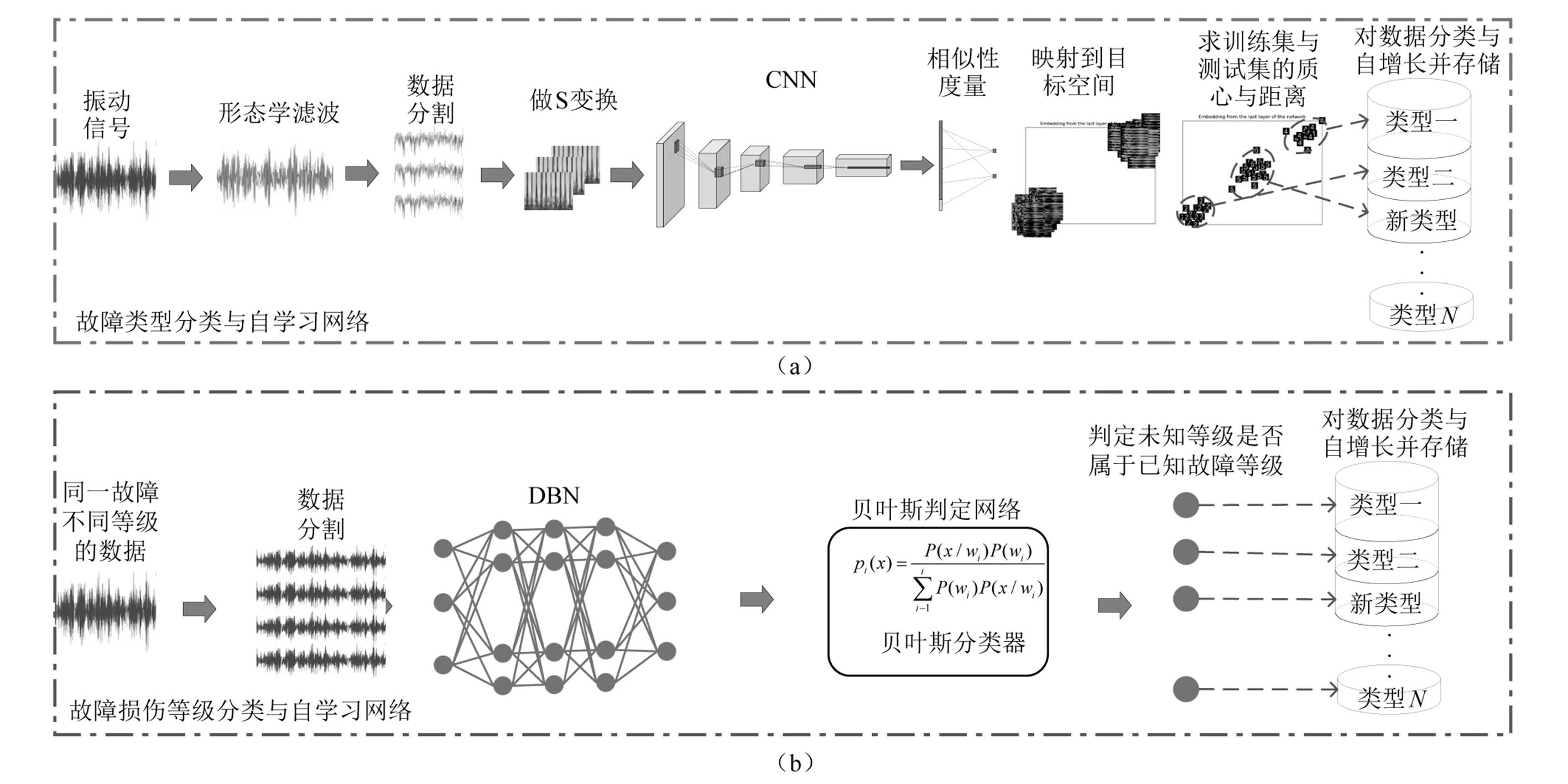
1.2 基于相似性度量与CNN相结合的故障自学习模型
2 故障损伤等级自学习模型
2.1 贝叶斯分类器

2.2 基于DBN与贝叶斯分类器相结合的故障损伤等级自学习模型

3 算法验证
3.1 实验平台介绍



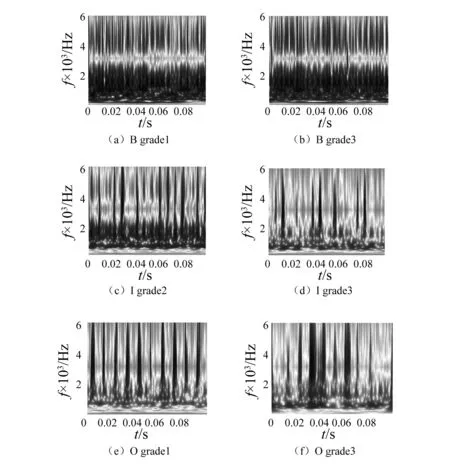
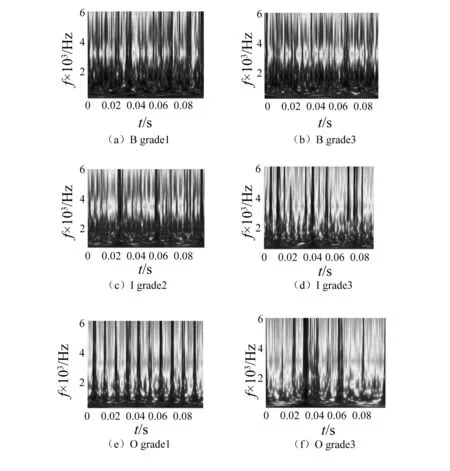
3.2 结果分析与讨论













4 结 论

