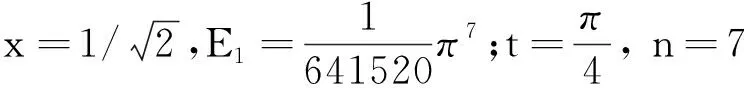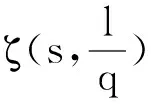分母含有奇平方因子的二项式系数倒数级数连带3个整数乘积倒数平方和
及万会,张来萍
(1.宁夏民族职业技术学院,宁夏 吴忠 751100; 2.宁夏大学 新华学院,宁夏 银川 750021)
1 引言及引理
二项式系数级数变换问题在组合数学、解析数学等学科研究领域极为重要,引起了很多组合专家的注意[1-10].一些作者用各种数学工具得到一系列二项式系数级数重要结果.它们在文中给出一些分母含平方因子的数值级数
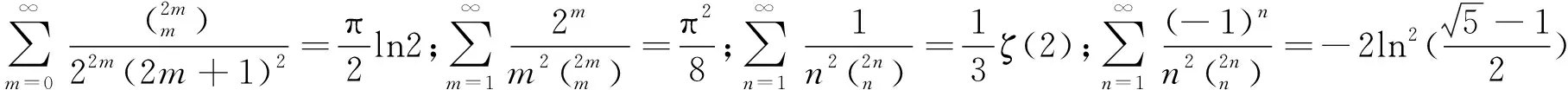

引理2[12]设p,q为正整数,1≤p 1)分母为奇平方因子的二项式系数倒数级数连带3个整数乘积倒数平方和 (1) (2) (3) (4) 2)分母为奇平方因子与1个线性因子乘积的二项式系数倒数级数连带3个整数乘积倒数平方和 (5) (6) (7) (8) (9) (10) 3)分母为奇平方因子与2个线性因子乘积的二项式系数倒数级数连带3个整数乘积倒数平方和 (11) (12) (13) (14) 4)分母为奇平方因子与3个线性因子乘积的二项式系数倒数级数连带3个整数乘积倒数平方和 (15) 级数变量用k+1代替k给出 两端关于x微分,可得 (16) 1)将(16)式左端裂项 令k-1=m,则 并将所有分式化成部分分式得到 由于E1已知,计算得出下面等式,并令其为E3. 2)将(16)式左端裂项 令k-2=m,则 并将所有分式化成部分分式得到 由于E1,E3已知,整理得到E5式. 3)将(16)式左端裂项 令k-3=m,给出 将所有分式化成部分分式得到 由于E1,E3,E5已知,整理得到E7式.定理1证毕. 积分变量替换,令x=sint,dx=costdt积分变量x范围(0,1),变量t范围(0,π/2),正整数满足1≤p 根据引理2文献[12],从而和式上标为[(7+1)/2]=4,[7/2]=3,n为奇数. 其中,ζ(s,l/q)为赫尔维茨zeta函数,ζ(n)为黎曼zeta函数. 为行文方便,令等式右端为D,给出 (17) 1)将(17)式左端裂项 令k-1=m,则 (18) (1)将(18)式分解成部分分式,得到 由定理1的E1,E3已知.整理得到(2)式并令(2)式为D3. (2)从(18)式直接得到(5)式. 用符号D3·1,D5·13表示.圆点前表示平方因子,圆点后表示奇因子. 2)将(17)式左端裂项 令k-2=m,则 (19) (1)将(19)所有分式分解成部分分式,得到 定理1的E1,E3,E5已知.代入上式,得到(3)式,并令(3)式为D5. (2)在(19)保留2个因子分式,然后对这些2个因子的分式,每次保留1个,其余化成部分分式,得到 由于定理1的E1,E3,E5和D5已知,计算上面2个等式得到(6)(7)式. (3)在(19)保留3个因子分式,其他分式化成部分分式得到 由于定理1的E1,E3,E5和D5已知,计算上面等式得到(11)式. 以A5·13证明级数连带3个整数乘积倒数平方和上标增加1项或几项不改变其和式收敛性. 前和式为二项式系数倒数级数连3个整数乘积倒数平方和表达式,后式极限趋于0. 所以,级数连带3个整数乘积倒数平方和上标增加1项或几项不改变其和式收敛性. 3)将(17)式左端裂项 令k-3=m,则 (20) (1)将(20)式所有分式化成部分分式,得出 由于E1,E3,E5,E7已知,计算得出(4)式,并令其为D7. (2)在(20)式中保留2因子的分式,其他分式化成部分分式,然后对这些2个因子的分式,每次保留1个,其余化成部分分式得到 由于E1,E3,E5,E7,D7已知,计算得出(8)(9)(10)式. (3)在(20)式中保留3因子的分式,其他分式化成部分分式,然后对这些3个因子的分式,每次保留1个,其余化成部分分式得到 由于E1,E3,E5,E7,D7已知,计算得出(12)(13)(14)式. (4)在(20)式中保留4个因子的分式,其他分式化成部分分式,得到 由于E1,E3,E5,E7,D7已知,计算得出(15)式.定理2证毕. [(7+1)/2]=4,[7/2]=3,用文献[12]第255页公式计算积分 则分母为奇平方因子二项式系数倒数级数连带3个整数乘积倒数平方和数值恒等式.
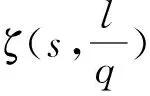
2 主要结果和证明
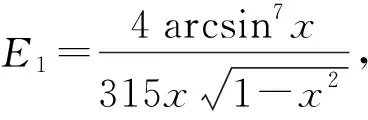
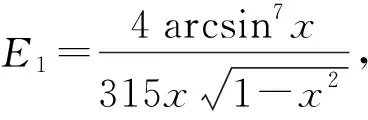
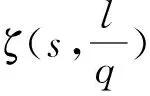


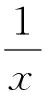



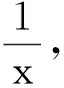


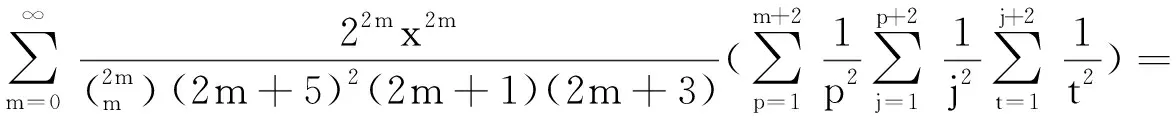

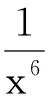
3 数值级数恒等式