不同基函数对LSM美式期权定价的影响

于 拓, 唐亚勇

(四川大学数学学院, 成都 610064)

1 引 言

不同于欧式期权，美式期权的期权持有人可以在期权到期日之前的任何时刻执行该期权.因此，我们无法用经典的B-S公式为美式期权定价.当前，对于美式期权的定价主要采用数值分析的方法.

对美式期权进行定价的常用数值方法有三类，其中的二项式方法和有限差分方法均采用逆向求解的方法.虽然它们可以用于美式期权定价，但是在处理具有多个标的资产的期权定价问题时这两种方法均表现不好.蒙特卡洛模拟方法虽然在处理多个标的资产的期权定价问题以及有关路径依赖的期权定价问题上具有明显的优势，但由于该方法采用正向求解方法，因而无法将某一时刻立即执行该美式期权的收益与继续持有该美式期权的期望收益相比较，从而导致在计算过程中无法确定是立即执行期权还是继续持有期权.2001年，Longstaff和Schwartz[1]提出了最小二乘蒙特卡洛法，解决了这一问题，进而该方法成为美式期权定价中最常用的一种方法.此后，许多学者对该方法进行了研究，如Guo和Loeper[2]讨论了应用多个多项式基的最小二乘蒙特卡罗模拟法；Joshi和Kwon[3]对具有小偏差和单向偏差的最小二乘蒙特卡罗的信用值进行讨论和调整；孙延维和雷建军[4]利用图形处理器优化实现了最小二乘蒙特卡洛模拟法的美式期权模拟定价系统；Mostovyi[5]分析了算法在行权日数增加时的稳定性，证明了如果股票价格的基本过程是连续的，等.

基于LSM算法，需要对当前标的资产价格S进行最小二乘回归.选择不同的基函数(通常是正交函数)将导致最终美式期权定价得到不同的结果[6-16].本文中我们将对不同的基函数对最小二乘蒙特卡洛法的影响进行讨论.

2 美式期权

与欧式期权不同，美式期权在合约到期前的任何时刻都可以执行.由此直观来看，美式期权持有者可以在期权到期之前的任意一天行权也就表示着美式期权持有者比欧式期权持有者享有更多权利，因而一般来说欧式期权的价格要小于美式期权的价格.其能否提前执行的标准是在某一时刻执行所获得的价值是否大于不提前执行所获得的价值，后者是后续存续期内期权的价值.值得注意的是，在期权的存续期内可能有多次提前执行的机会，而只有一次是最优的——只有一次可以使得期权的价值最大，此时的价值才是期权真正的价值.

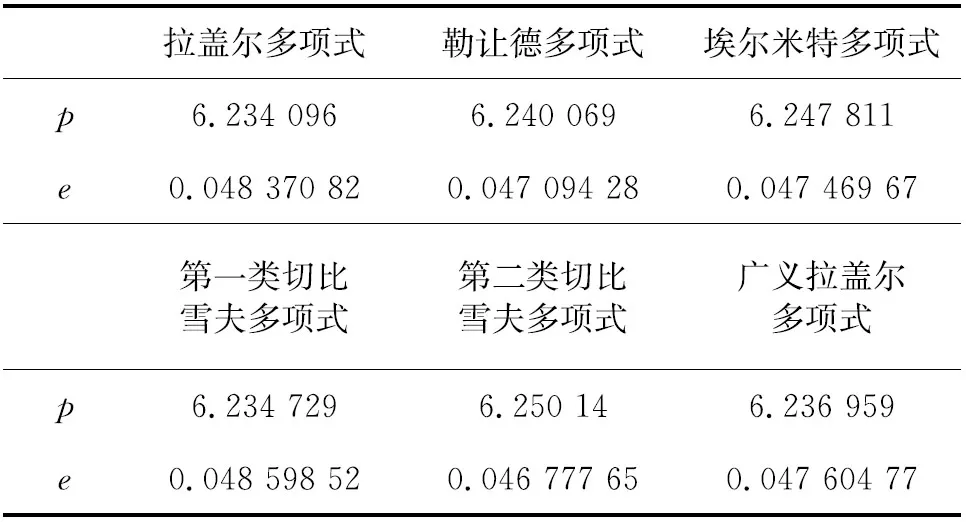
由于美式期权的连续性，在讨论美式期权时我们往往讨论另一种期权——百慕大期权，它可以在到期日前的某一固定时间点行权，也就是说在某一系列的离散时间中百慕大期权的价值可以由最优截止问题给出.对于某一有限时间点集合0

当t=tn时，即在最后行权时，百慕大期权的价格应该等同于和其有着一样标的欧式期权的价格，此时的欧式期权的价格可以由B-S方程给出，即Un=En=(K-Sn)+.由于百慕大期权可以在到期日前的某一固定时间点行权，所以我们需要找到一个使得执行美式期权以后可以获得最大利润的时停(最优时停).那么，在某一时刻tn，期权的持有者有着两个选择：

(i) 执行期权的收益En-1；

(ii) 保留期权的收益EQ[Un|Ftn-1]，

其中EQ为风险中性测度下的期望值(在风险中性概率测度下，任何期权的当前价值等于其未来支付期望值的折现)，F为一个σ-域.此时，某个百慕大期权在tn-1时刻的价值为

Un-1=max(En-1,EQ[Un|Ftn-1]).

问题的关键就变为求解EQ[Un|Ftn-1]的值，此时便可以用最小二乘法去近似求解.

3 正交多项式和LSM

运用最小二乘蒙特卡洛法(LSM)去近似求解美式期权最早由Longstaff和Schwarts于2001年给出.方法的核心就是经过引入最小二乘法来估计继续持有某一期权的价值的条件期望，再通过比较在某一时刻立即执行该美式期权所获得的收益与在该时刻所求得的继续持有期权的价值的条件期望的大小，从而得出对于该路径的美式期权的最优行权时刻.对于百慕大期权这种能够在离散时间点行权的情形，需要求解的问题则变为在未来某一个固定的时间点继续持有期权的价值的条件期望，这同样也可以用LSM法进行求解.于是，对于tn-1,tn-2,…t1中的某一时刻tm-1，EQ[Um|Ftm-1]可以表示为可列个Ftm-1可测函数的线性组合.不妨假设该条件期望属于Hilbert空间L2.则由最小二乘法有

EQ[Um|Ftm-1]=∑αjPj(X)，

其中X是一个马尔科夫过程，αj是一组常数，Pj是一组基函数.于是可以得到如下算法：

Step 1输入S0、K、T、σ、r、m、n,其中m为样本路径数，n为每年期 权可执行数;

Step 2生成一列服从标准正态分布的m维向量A(生成m条样本路径 数);

Step 3计算末尾的期权价格

及每个时期行权的收益(EV)

EVn=max(K-Sn,0);

Step 4从时间末尾开始逆向比较某一时期继续持有期权和行使期权的收益;

Step 4.1令i=n-1,计算Si与EVi，

其中

Δt=T/n,

EVi=max(K-Si,0);

Step 4.2计算此时继续持有期权的条件期望值(使用LSM法)

Step 4.2.1选择所有j使得EVi(j)>0,计算回归时所需的继续持有期权时的价值(HV)

HVi(j)=EVi+1(j)e-rT;

Step 4.2.2选取某一组正交多项式Lk关于HVi做最小二乘回归得到常系数a与回归系数ak;

Step 4.2.3计算此时继续持有期权的条件期望值E(HVi(j)),

E(HVi(j))=a+ak·Lk;

Step 4.3比较EVi(j)与E(HVi(j)),当EVi(j)

EVi(j)=EVi+1(j)e-rT;

Step 4.4i=i-1，i=0时停止;

Step 5计算期权价格

误差

该算法可以选取一系列不同的正交多项式作为该最小二乘回归的基函数，从而获取一系列不同的独立算法，进而比较不同的正交多项式对最终结果的影响.下面我们给出一些正交多项式并讨论其对LSM算法结果的影响.

拉盖尔多项式(Laguerre polynomials) 权函数

勒让德多项式(Legendre Polynomials) 权函数

w(x)=1,

P0(x)=1,

P1(x)=x,

埃尔米特多项式(Hermite polynomials) 权函数

w(x)=e-x2,

H0(x)=e-x2,

H1(x)=e-x2·x,

H2(x)=e-x2(x2-1),

第一类切比雪夫多项式(Chebyshev polynomials of the first class) 权函数

Tn+1(x)=2xTn(x)-Tn-1(x)；

第二类切比雪夫多项式(Chebyshev polynomials of the second class) 权函数

Un+1(x)=2xUn(x)-Un-1(x);

广义拉盖尔多项式(generalized Laguerrepolynomials) 权函数

w(x)=xαe-x,

分别用这些正交多项式作为最小二乘回归的基函数做LSM算法，并得出结果.

4 数值计算

取现价S0=36，期权协议价K=40，期权年限T=1，波动率σ=0.2，无风险利率r=0.06，样本路径数m=1 000，每年期权可执行数n=50T.使用R语言进行编程设计，计算结果如表1所示.

表1 第一个算例的计算结果

当我们改变参数而得到多组数据时，取S0=38,K=40,T=1,σ=0.2,r=0.06,m=1 000,n=50T，计算结果如表2所示.

表2 第二个算例的计算结果

再取S0=40,K=40,T=1,σ=0.4,r=0.06,m=1 000,n=50T，计算结果如表3所示.

表3 第三个算例的计算结果

最后，我们取S0=42，K=40，T=2，σ=0.4，r=0.06，m=1 000，n=50T，计算结果如表4所示.

表4 第四个算例计算结果

通过对参数进行不同选取，我们可以看出，选取不同的正交多项式作为基函数时其对得出的最终定价p和误差e略有差异.综合来看，勒让德多项式(Legendre Polynomials)表现最好，第一类切比雪夫多项式(Chebyshev polynomials)表现较差.

本文主要讨论使用最小二乘蒙特卡洛法(LSM)为美式期权定价时选取不同正交多项式作为基函数对最终结果的影响.首先，我们简单介绍了美式期权(为了简化模型而选用百慕大期权近似美式期权)及最小二乘蒙特卡洛法(LSM).在给出算法后，我们计算不同正交多项式作为基函数下使用最小二乘蒙特卡洛法对美式期权定价的结果.值得注意的是本文所使用的B-S模型过于理想化，并不符合实际应用计算.此外对于最小二乘法的改进形式如偏最小二乘法、加权最小二乘法也可以作进一步讨论.