纵掠平板速度和温度边界层湍流转捩区的积分方法

赵 波， 刘 建， 李开勇

(四川大学机械工程学院 空天动力燃烧与冷却教育部工程研究中心， 成都 610065)

1 引 言

边界层由简单稳定状态的层流向具有强烈非线性现象、多尺度效应的湍流过渡区域称为转捩区. 长期以来，边界层转捩一直是流体力学中最重要的前沿问题和难点之一[1-4]. 边界层转捩伴随着壁面摩擦和传热特性的急剧变化，减小飞行器表面摩擦阻力和热流、燃气涡轮发动机叶片冷却和燃烧时燃料掺混效率等问题均与转捩特性密切相关[5-6]；转捩对揭示湍流真正形成机理也具有重要价值[7]. Reynolds最早通过圆管实验发现有层流和湍流两种不同流态，这被视为研究边界层转捩问题的肇始. Emmons[8]发现转捩区间歇出现的湍斑，它们沿流动方向不断变大增多，最终在完全湍流区布满，这表明边界层转捩区以间歇出现的湍斑为主要特征. 为此，Dhawan和Narasimha[9]提出间歇因子的概念以描述转捩区湍斑的分布特征：间歇因子为0时流动为层流，为1时则代表完全湍流，他们以间歇因子为加权系数, 可将任意位置的流场视为层流与湍流的线性组合[10]，这种叠加思想能较好地预测零压和顺压梯度的转捩过程[4]，但并未考虑层流与湍流间的相互作用. 针对这个不足，Libby[11]采用条件平均法，通过建立含间歇因子的输运方程加以解决. 张若凌等[12]采用热力学平衡系统连续相变方法，类比研究了管内转捩区的流动和振荡特性，视转捩流动为层流和湍流的线性组合，所提出的合成系数考虑了振荡特性. Langtry等[13-14]发展了完全由局部变量构造的新型模式,使转捩计算与流场结构直接相关，与Coupland[15]的空气外掠平板转捩实验的结果对比表明准确性较高. 董平等[16-17]在上述模型基础上，分别对外掠平板边界层转捩区的速度和温度进行了数值计算，并与Coupland[15]试验结果进行了比较. 针对完全湍流流动，Prandtl和Taylor沿边界层厚度方向将边界层划分为层流底层和湍流核心区，提出分别描述速度和温度边界层的Prandtl-Taylor两层模型；von Kármán进一步在层流底层和湍流核心区中间增加了缓冲层，建立了三层模型. Khademi等[18-19]采用完全湍流边界层的两层模型，通过积分方法分别建立了动量方程和能量方程，获得的速度场和温度场分布规律与以往理论结果一致性较好. 最近，Lozano-Durán等[20]利用非线性抛物化理论预测了转捩的起始位置，预测结果与大涡模拟(LES)和直接数值模拟(DNS)计算吻合度较高. 由上可见，目前对边界层转捩区的研究多以数值模拟方法为主，通常计算量较大(如LES和DNS相当于Re9/4[3])，由于问题的复杂性，采用理论研究的方法相对较少. 就作者所知，目前为止尚未发现采用积分方法预测边界层自然转捩区的速度和温度场分布方面的理论研究. 为此，本文在以往研究基础上[21-22]，将以空气外掠平板边界层为研究对象，采用完全湍流区的两层模型思想，首先将转捩区沿边界层厚度方向划分为层流底层和准湍流层，然后在准湍流层利用间歇因子定量描述该区域的湍流时间份额，最后利用积分方法，分别建立转捩区的动量方程和能量方程，以获得边界层转捩区速度场和温度场的理论分布，同时将之与Coupland实验结果和数值仿真模型相比较，以证明理论模型的正确性. 边界层转捩最关注的因素有三：转捩的起始位置、转捩区长度和转捩区内的时均流动特性[23]. 本文将仅限于转捩区的时均流动特性和温度场分布规律的讨论，研究对象限于零压力梯度条件下外掠平板的自然转捩特性.

2 理论模型

2.1 转捩边界层积分方程组

首先，这里讨论的流体指粘性流体，根据牛顿内摩擦定律、层流理论和Prandtl-Taylor湍流边界层的两层理论[24]，靠近壁面的区域因液体粘性的存在，可近似认为是层流流动[10]，故有理由认为对于从层流向湍流过渡的转捩区也应如此，为与完全湍流的“层流底层”称谓相一致，仍称转捩区的近壁面区域为“层流底层”(laminar sublayer)，如图1所示. 其次，根据间歇理论[8-10]，转捩区内的湍斑在流动方向上逐渐增多，直到在完全湍流区布满，若遵照完全湍流区的Prandtl-Taylor两层理论，布满湍斑的区域应仅限于湍流核心区而不包含层流底层；类似地，这里假设在转捩区内，只有外层区域(从层流底层外缘到主流区)内存在湍斑，为方便，称之为“准湍流层”(quasi-turbulent layer)，如图1. 最后，根据Langtry和Menter[13-14]的观点：用动量厚度雷诺数来判断转捩的开始，用间歇因子来描述转捩的过程[3]，假设转捩区初次出现湍流的位置在动量边界层最大厚度δ*处，如图1，并假设：(1)常物性和不可压缩流体；(2)准湍流层湍斑在主流方向的脉动速度、脉动温度与完全湍流区规律相同[12]；(3)零压力梯度和常壁温，忽略耗散热；(4)经计算可知，层流底层和准湍流层的速度边界层厚度非常接近温度边界层的对应厚度，为积分方便，设层流底层和准湍流层的温度边界层厚度Δ1和Δ略大于速度边界层的对应厚度δ1和δ；(5)只考虑自然转捩情况，为与Coupland实验结果相比较[14-15]，设转捩起始位置雷诺数为105，在该位置处的层流底层厚度记为δ*，如图1.

图1 空气外掠平板转捩区边界层的两层模型示意图

图2给出转捩区控制体积示意，区域1-2-3-4为层流底层，3-4-5-6为准湍流层，l为流体厚度，dx为x向微元. 因dx极小，认为层流底层厚度δ1在dx内沿x向近似不变.

图2 转捩区控制体积微元

根据动量守恒定理，采用与层流边界层类似的积分方法[24]，最后获得到外掠平板转捩区的动量方程为:

(1)

式中ρ为流体密度(kg/m3)，μ为动力粘度(Pa·s)，δ1、δ分别为层流底层和准湍流层速度边界层的厚度(m)，见图1，u1、u2分别为层流底层和准湍流层的时均速度(m/s)，uL和u∞分别为层流底层外缘处和主流区的速度(m/s). 根据能量守恒定理，采用完全类似的积分法[24]，得到能量方程为:

(2)

式中c为定压比热容[J/(kg·K)]，λ为导热系数[W/(m·K)]，Δ1、Δ分别为层流底层和准湍流层温度边界层的厚度(m)，T1、T2分别为层流底层和准湍流层的时均温度(K)，TL和T∞分别为层流底层外缘处和主流区的温度(K).

2.2 速度分布函数

认为外掠平板转捩边界层具有相似的速度分布，设在层流底层(0≤y<δ1)和准湍流层(δ1≤y<δ)的时均速度分布具有如下形式:

(3)

式中ai(i=1～5)为待定系数，m为正的常数.

(4)

γ=1-e-0.412(x-xt)2/χ2

(5)

式中xt为转捩区起始位置，由临界雷诺数确定；χ=x|γ=0.75-x|γ=0.25，由文献[8]中零压力梯度条件下外掠平板转捩边界层的实验数据确定.

由上述边界条件式并考虑方程(4)和(5)，最终确定方程(3)中的待定系数为:

a1=a3=0,

a5=u∞δ-1/m.

相应地，转捩区的速度分布式(3)可写为:

(6)

2.3 温度分布函数

同样地，认为转捩边界层具有相似的温度分布，考虑假设(3)，设层流底层和准湍流层的过余时均温度分布为:

(7)

b1=b3=0,

相应地，转捩区的时均温度分布式(7)可写为:

(8)

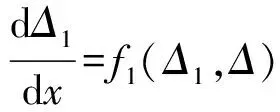
3 有限元模型和常数m、n的选择

3.1 有限元模型

以外掠平板的空气为研究对象，在Fluent软件中采用如图3所定义的有限元分析区域：平板长度取3 600 mm，空气域高度取220 mm. 所研究的转捩边界层位于平板近壁面，需精确计算近壁面速度和温度变化情况，经仔细比较[26-28]，最终选取FLUENT软件中的SSTk-ω模型作为数值计算的转捩模型.

图3 空气外掠平板数值计算区域

为了同Coupland实验结果[14-15]比较，取自由流速度和温度分别为u∞=5.3 m/s和T∞=293 K，常壁温Ts=323 K. 空气入口位于数值模型最左端，空气出口分别位于模型最右端和空气域上方，两者皆采用零压力出口，如图3. 二维有限元模型采用四边形面单元，考虑到所关注的边界层仅存在于平板近壁面极薄区域，为节省计算资源且保证求解精度，取网格全局尺寸10 mm，在平板垂直距离60 mm内设置40层网格，每层网格以1.2倍速度增加，总单元数19 712，总结点数20 121，如图4所示. 根据假设(5), 转捩起始位置处的雷诺数为105，针对上述给定参数，数值和理论计算的结果表明，转捩边界层结束时的雷诺数为3×105.

图4 空气外掠平板有限元模型网格

3.2 常数m、n的确定

由第1部分可知，在转捩边界层的准湍流层速度和温度分布式(6)和(8)中，幂指数项1/m和1/n的大小对理论预测至为关键. 为此，经过大量计算、选择和对比，限于篇幅，仅以m(或n)分别取7、7.5和8为例阐述之. 同时，将本文理论结果与Coupland平板转捩实验和上述数值模型的结果相对比，以选取合适的m和n常数值.

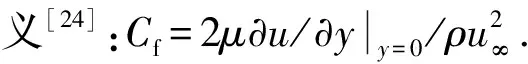
图5 转捩区内壁面的局部摩擦系数

图6 转捩区时均速度沿边界层厚度方向的分布

图7给出转捩区时均温度沿边界层厚度方向的变化，通过对比发现，温度当n=7时理论解与数值解(以之为benchmark)最接近. 因此最终确定：选取m=7.5，n=7.

图7 转捩区时均温度沿边界层厚度方向的分布

相应地，速度和温度分布式(6)(8)变为

(9)

(10)

由转捩边界层的动量厚度ϑ的定义[9, 24]，有:

将式(9)代入上式，若不考虑间歇粘度比ϖ沿y向的变化，转捩区的无量纲动量厚度可表示为:

由上式可直接写出动量厚度雷诺数的显式表达式.

4 Dhawan和Narasimha的线性叠加思想

为后面对比方便，这里简要介绍一下Dhawan和Narasimha关于转捩区的线性叠加思想. 根据间歇理论[9-10]，以间歇因子γ为权重系数，转捩边界层的速度和温度分布可以线性叠加为下式：

u=(1-γ)uL+γuT

θ=(1-γ)θL+γθT

(11)

式中uL、uT分别代表层流速度和完全湍流流动时的时均速度，θL、θT分别是层流过余温度和完全湍流的过余时均温度. 对于层流和湍流的速度分布，这里分别采用von Kármán的层流边界层的积分解和1/7幂律[24, 29]，即

同样地，由式(11)容易推导出转捩区努塞尔数Nu可由层流和完全湍流的努塞尔数线性叠加得到：

Nu=(1-γ)NuL+γNuT

(12)

其中层流努塞尔数NuL=0.332Pr1/3Re1/2[24], 湍流努塞尔数NuT=0.0287Pr0.6Re0.8[30]. 为方便，以下称方程(11)和(12)为D-N解.

5 结果讨论

5.1 转捩边界层厚度

图8给出了通过动量积分方程组(1)获得的外掠平板动量边界层中层流底层和准湍流层厚度的理论分布. 由图8可见，层流底层从层流边界层的最大厚度δ*(=0.0049 m)处开始突降，直到转捩区结束(这里转捩区结束时雷诺数为3×105)后进入完全湍流区，而准湍流层则从相同的边界层厚度δ*处开始骤增，直到转捩区结束后进入完全湍流区. 图9给出了通过能量积分方程组(2)获得的外掠平板热边界层中层流底层和准湍流层厚度的理论分布(其中Δ*=0.005 4 m)，主要结论与动量边界层类似，不赘述.

图8 速度边界层中层流底层和准湍流层的厚度

5.2 时均速度

图10给出x位置固定时(Re=2.5×105)，外掠平板转捩区内空气的时均速度沿边界层厚度方向的分布. 由图可见，本文理论解与D-N解大体上符合得很好，尤其在准湍流层区域，而在层流底层内二者略有偏差.

图10 时均速度沿转捩边界层厚度方向的分布

图11给出了平板不同x位置处(对应不同的γ)的时均速度分布情况. 由图可见，γ表观上对近壁面的层流底层速度分布有更大的影响，这与本文理论公式(9)，以及Dhawan和Narasimha[9]的发现相一致：即γ主要影响x方向的时均速度分布，且在近壁面区域影响相对明显. 进一步观察发现，γ对远离壁面的准湍流层速度分布完全没有影响，这是由于图中采用无量纲厚度y/δ坐标的缘故，实际上不同的γ会导致不同的δ，具体见公式(9). 注意到图11中的速度呈相似性分布，γ=0和γ=1曲线分别代表层流和完全湍流流动两种特殊情况，其中γ=0代表的层流是计算转捩开始的初始条件，转捩开始后，当x(和γ)稍有所增大，速度的变化就十分剧烈，这符合转捩区速度(和壁面摩擦系数)的突变骤增的特点，注意到速度总体分布与文献[9]中的图11结果几乎完全相同，只不过后者采用了另一个无量纲厚度y/ϑ作为横坐标，相当于放大了图11中的层流底层区域.

图11 间歇因子γ对无量纲时均速度的影响

图12给出了无量纲速度在转捩区层流底层和准湍流层随间歇粘度比ϖ参数变化情况. 由图12可见，除转捩刚开始时层流底层速度骤升外，其余大部分情形均是速度随ϖ增加而减小，且两个区域下降幅度非常相似. 这是因为：根据间歇粘度比ϖ定义，y固定时ϖ只与间歇因子γ(或x)有关，当γ(或x)增大时无量纲厚度y/δ变小，由图10易知时均速度也相应减小.

图12 间歇粘度比ϖ对无量纲时均速度的影响

5.3 时均温度

图13给出x位置固定时(Re=2.5×105)时均温度沿边界层厚度方向的分布. 由图可见，同无量纲速度的分布几乎完全相同，本文理论解与D-N解大体上符合得很好. 图14和15给出了平板不同x位置处(对应不同的γ，y固定时也对应不同的间歇导温比ψ)的时均温度分布，主要结论与前面无量纲速度的分布情形非常相似，不赘述.

图13 时均温度沿转捩区边界层厚度方向的分布

图14 间歇因子γ对无量纲时均温度的影响

5.4 壁面摩擦系数

根据Blasius公式[24]，层流时壁面摩擦系数CfL=0.664Re-0.5；由Prandtl-Schlichting理论公式[24, 29]，完全湍流时的壁面摩擦系数CfT=0.0587Re-0.2. 基于间歇理论，Emmons[8]以及其他学者[9]给出了转捩区壁面摩擦系数Cft公式：Cft=(1-γ)CfL+γCfT，为方便，称之为Emmons解.

层流向湍流转捩最显著的特征是：壁面摩擦系数取得极小值处转捩开始，在转捩区内突变骤增，转捩结束位置处达到极大值，且略大于完全湍流时的壁面摩擦系数CfT，随后进入完全湍流，壁面摩擦系数缓慢减小，该特征也是转捩实验中最易监测的变量(见图16). 将本文理论解和数值解获得的局部摩擦系数，同Coupland实验结果、层流和完全湍流理论解以及转捩区的Emmons解进行了对比，如图16. 由图16可见，本文的理论解与试验结果符合得非常好，转捩区内最大相对误差为4.8%，数值解也与试验结果大体符合. 注意到转捩区内Emmons解与试验值相比偏差相对更大，这表明用积分方法获得的理论解同以往用层、湍流叠加的方法(即Emmons解)具有较大优势.

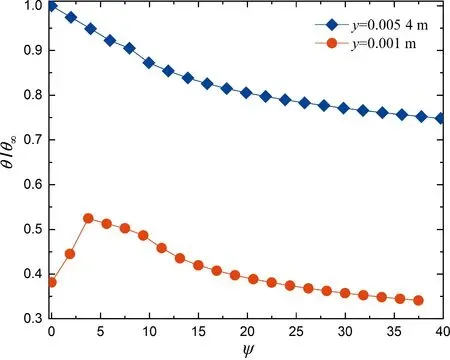
图15 间歇导温比ψ对无量纲时均温度的影响

图16 平板壁面摩擦系数分布

5.5 努塞尔数

图17给出了代表壁面传热特性的努塞尔数沿主流方向的分布情况，发现同壁面摩擦系数在转捩区内突变骤增的特征不同，努塞尔数在转捩区虽有变化，但波动要相对小得多. 图17将本文理论解和数值解获得的局部努塞尔数，同D-N解进行了对比，结果表明理论解和D-N解及数值解结果符合得非常好，在转捩区内最大相对误差分别为3.9%和5.3%，再一次证明了理论模型的正确性.

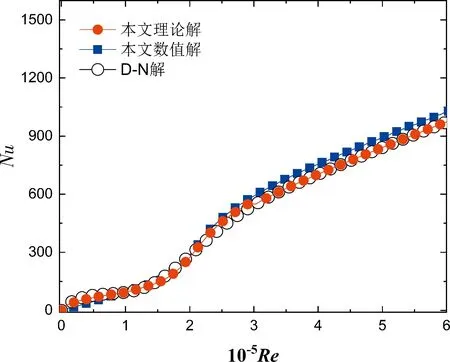
图17 局部努塞尔数分布Fig.17 Profiles of local Nusselt numbers

6 结 论

以常壁温、零压力梯度的外掠平板空气为研究对象，将自然转捩边界层沿厚度方向划分为层流底层和准湍流层两部分，采用积分方法，分别建立了关于速度和温度的动量和能量积分方程组，并获得了速度场和温度场的显式表达式，通过四阶龙格-库塔算法获得了动量和热边界层厚度大小，同时与数值解、D-N解和实验结果加以对比表明，在给定条件下，通过理论解获得的表面摩擦系数和努塞尔数与benchmark结果的最大相对误差在4.8%以内，证明了理论模型的正确性，主要结论如下：

(1) 利用相似假设和湍流边界层厚度分层思想，分别采用三次多项式和1/m(或1/n)幂指数函数代表转捩区层流底层和准湍流层的速度场和温度场的分布规律，发现常数m=7.5、n=7时具有较好的理论预测精度.

(2) 速度和温度理论公式表明，间歇因子不仅对边界层(准湍流层)厚度有影响，尤其对“层流底层”的厚度、速度和温度分布具有关键影响，因此，该底层不是真正的层流流动；参数分析表明，所提出的间歇粘度比ϖ和间歇导温比ψ是影响转捩区速度和温度场分布的关键参数.

(3) 解析模型从理论角度再次证实，在转捩区表面摩擦系数具有突变骤增的显著特征，而且在转捩起始和结束位置处分别取得极小值和极大值. 而努塞尔数(对流换热系数)在转捩区的变化远没有壁面摩擦系数的变化显著，因此表面摩擦系数应视为判断边界层转捩起始位置和结束位置的关键指标. 以上结论同样有潜力用于外掠多孔壁面转捩边界层的发散冷却等相关转捩问题研究中.