多元表征 整体建构——对一年级学生理解减法意义情况的调查与分析

□ 李国良

在“减法的认识”教学过程中，教师一般把重点放在计算或解决具体问题上，较少关注学生对减法意义的理解和减法模型的建构水平。为了解这两方面的真实情况，笔者通过分析教材、前测等方式对学生进行了调查研究。

一、调查前的思考

（一）“减法模型”有哪些类型

依据问题中的关系可以把减法模型分成三类，分别是“部分—部分—全体”型问题、“改变型”问题、“比较型”问题（如图1）。

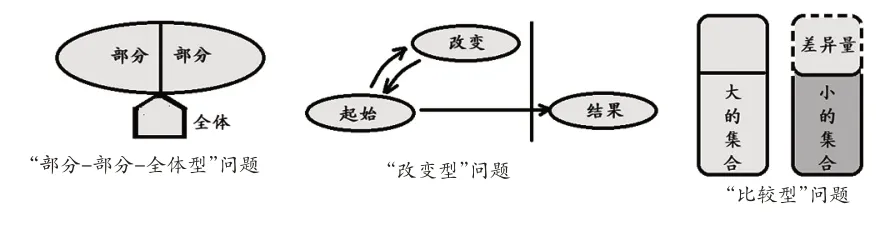
图1

1.“部分—部分—全体型”问题

这类问题指的是将一个整体分为若干个部分，已知全体和其中的某部分，求其他部分的问题。如：数学兴趣小组有5 名学生，其中有3 名男生，有几名女生？

2.“改变型”问题

这类问题指的是起始数量（起始量）增加或减少了一部分（改变量），得到了一个结果（结果量）的问题。在减法中，根据未知量的不同可以分为三种形式——求减少后的量、求增加前的量以及求改变量。如，求减少后的量：小红有5只苹果，吃了3只，还剩几只？求增加前的量：小红有一些钱，妈妈给她3元后，小红有5元了，小红原来有几元钱？求改变量：小红有3 元，妈妈给她一些钱后，小红有5 元了，妈妈给她多少元？

3.“比较型”问题

这类问题指的是对两个量进行比较产生的问题。比较时会有较小、较大和差异三个不同量，在这三个量的关系中，有两种类型的问题要用减法解决：一种是求相差量，另一种是求较小量。如，求相差量：小明有5 元钱，小红有3 元钱，小明比小红多几元？求较小量：小明有5 元，小红比小明少3 元，小红有几元？或小明有5 元，比小红多3 元，小红有几元？这两种求较小量的问题，对学生来说，体现出的思维层次不同，前一种题目，学生的认知结构和题目呈现的逻辑结构一致，可称作“求较小量的顺向问题”；而后一种题目，学生的认知结构和题目呈现的逻辑结构不一致，可称作“求较小量的逆向问题”。逆向问题对学生的思维水平要求更高。

（二）教材中如何呈现

根据减法意义的三种模型，对现行人教版教材一至六年级中有关减法的例题进行了梳理与分类。

1.减法意义以板块式分布

小学教材中与减法直接相关的知识点主要涉及整数减法、小数减法和分数减法。与减法意义相关的内容集中安排在一、二年级的整数加减法中，也就是学生会在一、二年级初步理解减法的意义，而到四年级“四则运算”单元中才学习减法的概念。

2.减法模型以穿插式构建

教材以穿插的方式呈现减法的三种类型。第一次出现减法是在一年级上册“1～5的认识和加减法”中，情境是：4 个气球飞走1 个，还剩几个，即教材中关于减法意义的内容是从“改变型”问题（拿走）开始呈现的；随后在本单元练习中出现了借助于数数及一一对应来学习的“比较型”问题，情境是：上面一排5 只小鸡，下面一排3 只小虫，问题是小鸡比小虫多___；第5单元开始出现“部分—部分—全体型”问题，情境是通过图文呈现，一共有6只企鹅，可以看到右边有4只，左边被东西遮挡住了，问左边有几只。综上可见，一上年级已经呈现了减法的三种模型。值得注意的是“比较型”问题在一年级中只呈现求相差数的问题，到了二上年级，在“100 以内加减法（二）”中出现了“比较型”问题中求较小量的顺向问题，到五上年级“简易方程”单元中才出现“比较型”问题中求较小量的逆向问题。

另外，三种减法模型（除“比较型”问题中求较小量以外）都出现在“数的认识”知识点后，教材呈现时都借助了情境图，以帮助学生更好地理解减法意义。因此，教学时要关注数数、数的组成等内容，并借助这些内容帮助学生理解每一种减法模型的意义。

二、学情调查与分析

选取同一区域内134 名学生，从两个层面、四个维度对他们理解减法意义的情况进行调查。第一层面是考查学生用图示或情境来表征减法意义的情况；第二层面是考查学生将图例或文字描述抽象成算式的水平。

（一）用图示表征减法意义的水平分析

测试中，要求学生用两个不同的图示表征“5-3”的意思，以考查学生用图示表征减法意义的情况，统计结果如表1所示。

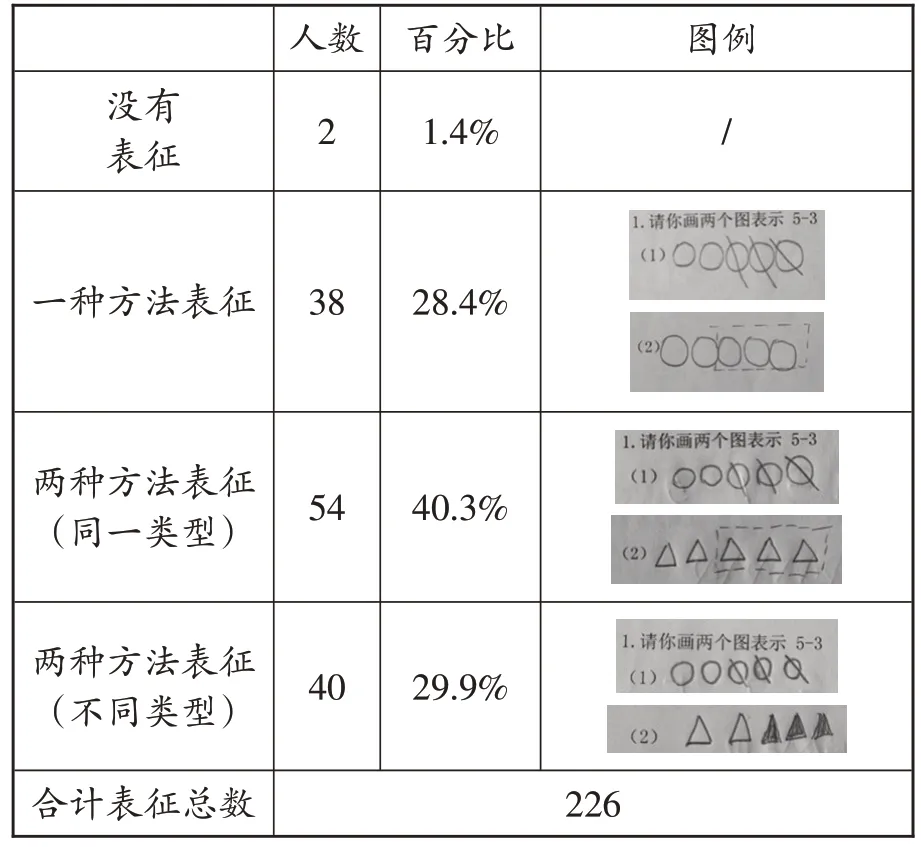
表1 图示表征算式能力水平统计表

从表1中可以发现：能用两种不同方法表征减法意义的学生只占学生总人数的29.9%，而40.3%的学生画了两个图示，但表征的内容属于同一类型，说明多数学生还没有建立对减法的“类”的感知。同时，在226 份表征图中，有186 份采用“改变型”问题的方式（用画去、圈走等方法）来解释减法的意义，仅有40 份采用了“部分—部分—全体型”问题的方式来解释5-3 的意思，而没有学生采用“比较型”问题的方式来解释减法。这说明在用图式表示减法意义的三种模型时，学生最熟悉的是“改变型”，而“比较型”和学生的心理距离最远。同时，用“改变型”解释减法意义的图示，多数（178份）都是用圆圈等具体的图形来表示数，极少数（8份）采用小棒图或计数器来表示（如图2、图3），或许在其中可以看到教学对这部分学生产生的影响。

图2

图3

（二）用情境描述减法意义的水平分析

测试内容为：要求学生根据算式“5-3”编写两个不同的情境来阐述算式的意义。以考查学生用情境描述减法意义的情况，统计结果如表2所示。

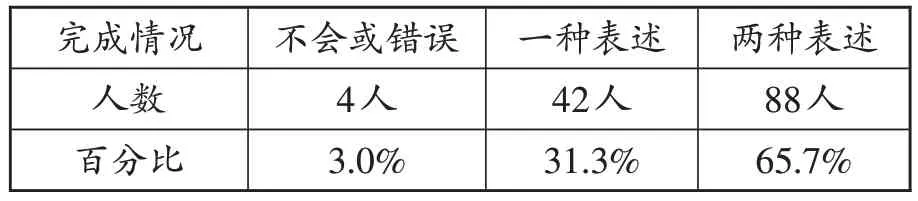
表2 情境描述减法意义的数据统计表

从表2的数据中可以看出，97%的学生都能用一种或两种情境描述减法的意义。但与用图式表征不同的是，用情境描述减法意义时，学生的表征类型集中在“改变型”问题和“比较型”问题上，却没有学生采用“部分—部分—全体型”。其中，编写出的218道题目中，有101道是“……飞走了（吃掉了）……还剩几个？”这种求还剩多少的类型，占总题数的46.3%，有95 道是直接用文字表达“5 比3 多几个？”或“3比5少几个？”占总题数的43.6%。

在上述两个维度的书面调查后，教师有针对性地选取了每班5 位（共20 位）学生进行访谈。访谈的内容为“你觉得什么是减法？”访谈中发现，78%的学生能模糊地说出“从一堆东西里拿掉一部分”，也就是学生对减法意义的理解更多建立在“拿走、飞走、吃了”等生活中的动态思维中，这是减法产生的原基础。

（三）将图例表征抽象成算式的水平分析

为考查学生根据图例，写出相应的减法算式的能力，对学生进行了“看图写算式并计算”的调查。调查试卷中共有10道题目，其中7道需要用减法解决。统计结果如表3所示。

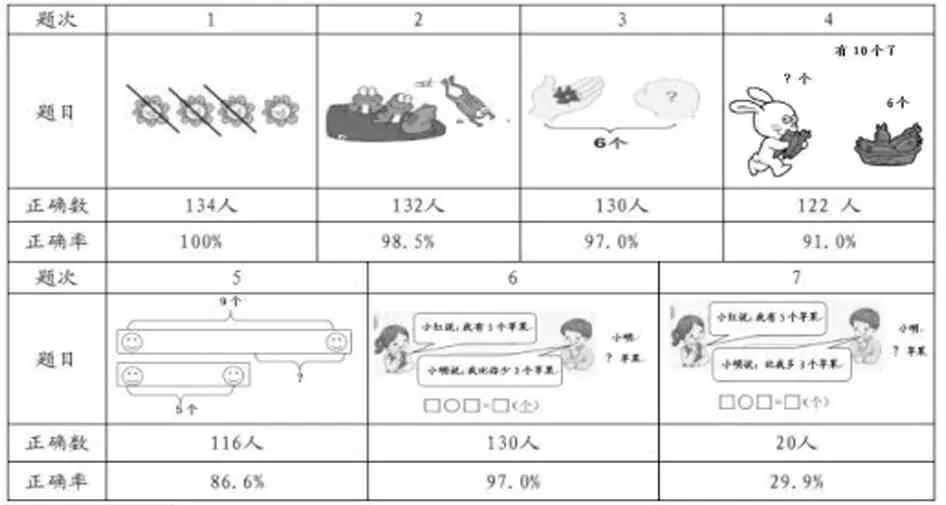
表3 图例抽象算式能力水平统计表

从表3 中发现：学生解决“部分—部分—全体型”问题（第3 小题）与“改变型”问题（第1、2、4 小题）时，正确率都比较高。尤其是第1小题，正确率为100%，这与前文中，请学生用图式表征减法意义，学生更喜欢用画去圆形的方法表征减法意义相一致。这几道题目中，相对来讲，求改变量的第4小题有9%的学生出现错误，错误率较高。仔细分析发现，其中6.0%的学生把求结果量与求改变量相混淆，写成了“10-4=6”，也就是说他们对起始量、改变量与结果量三者之间的关系是清晰的，只是表征关系的算式与“习惯”不符，只有3.0%的学生把算式写成了“10+6=16”，这3%的学生才是对三种量之间的关系理解不到位。

第5、6、7小题属于“比较型”问题模型，分别是求差异量、求较小量的顺向问题和求较小量的逆向问题。其中，第7小题是所有题目中错误率最高的题目，有70.1%的学生将算式列成“5+3=8”，访谈中发现，题目中的“多”字对学生的影响很大，也就是说，这部分学生对谁与谁比、谁比谁少中，哪一个“谁”才是比较的标准还不够清晰。

（四）将文字描述抽象成算式的水平分析

为考查学生将纯文字表征的题目抽象成算式的能力，进一步了解学生对减法意义的理解，对学生进行了“先用图式表示题目内容，再列式计算”的测试，与“将图例表征抽象成算式”的测试一样，共测试10小题。统计结果如表4所示。

测试结果同样显示学生解决“部分—部分—全体型”问题（第3小题）与“改变型”问题（第1、2、4小题）时，正确率较高，而解决“比较型”问题尤其是“求较小量的逆向问题”（第7 小题）出错的人数最多，正确率只有77.6%。同时发现，学生用算式解答的正确率高于用图式表征题目意思的正确率，尤其是第7小题，没有学生能用图式正确表征出题目的意思，这当然可能与教材的安排有关，但同时也说明比较型问题涉及两个量之间的关系，一上年级学生要理解两个量（两个数）之间存在的关系确实有困难。

三、调查后的启示

（一）要整体构建减法意义三种模型

所谓整体思维，就是要把各个部分按照一定的秩序组织起来，以整体和全面的视角把握对象。本次调查与分析，虽然是根据减法意义的三种模型，从不同角度展开，但事实上，减法意义的分类与模型的建构，并不是让减法意义的理解从类型的角度割裂开来，而更需要教师用整体的视角有深度地去把握，去架构不同模型，使学生能从一种模型联想到另一种模型，达到模型间的互相连通，真正把减法的意义理解透彻。

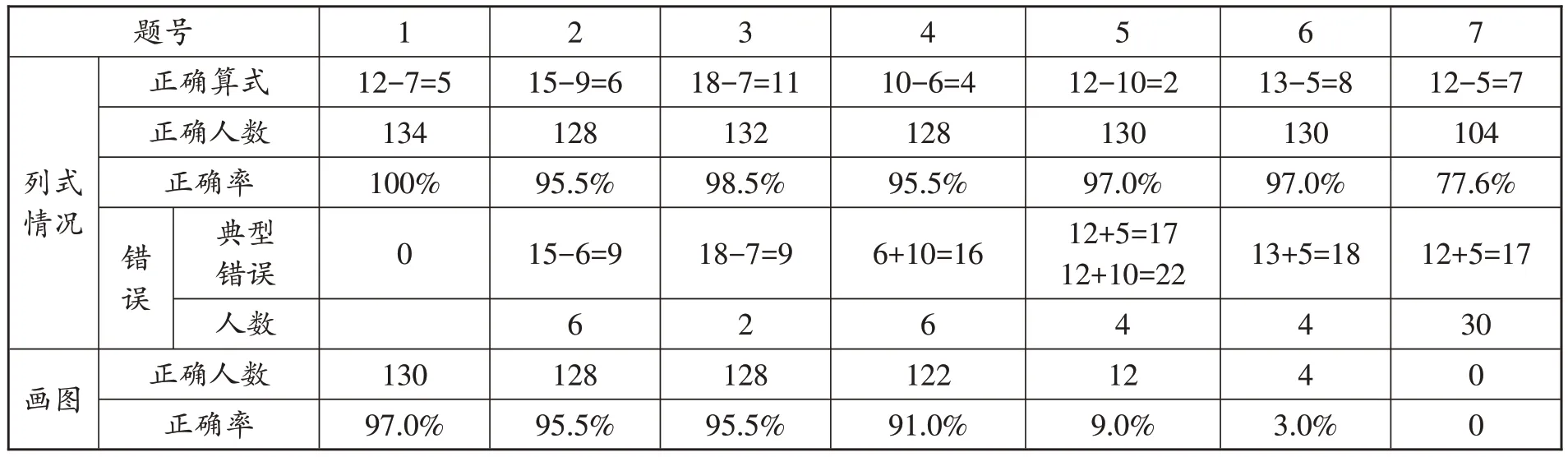
表4 文字抽象算式能力水平统计表

教学时，可以从减法的生活原型（拿走的）入手，把“改变型”问题与“部分—部分—全体型”问题建立起一个整体框架（如图4）。

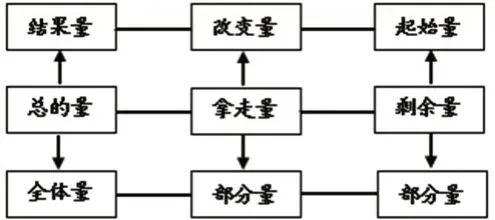
图4

“改变型”问题中的起始量相当于“部分—部分—全体型”问题中的总量，当把拿走的部分看作是一种改变时，另一部分就是剩余量；如果把一部分看作是结果量，那么另一部分就是改变量。

“比较型”问题的三种形式也可以与“部分—部分—全体型”问题构建起一个框架（如图5）。

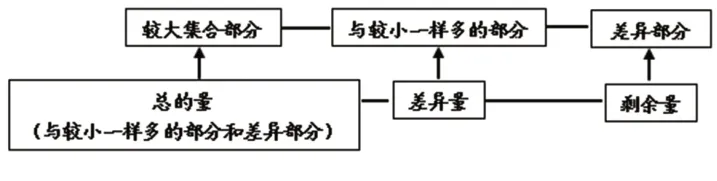
图5

这样学生会对减法有一个整体性的感知，对减法的认知过程会成为一个系统化的过程，能凸显减法知识内外纵横的结构关联，突出减法认知过程和思维方式深入的融通，结构化地理解减法意义。

（二）要重视引导学生经历多元表征过程

在数学学习活动中，数学表征起到了极其重要的作用，数学表征能力发展在很大程度上影响着学生的认知水平。模型、文字、符号等是基本的表征形式，每一种表征都能用来表达任意一种运算的关系，帮助学生发展运算意识。如算式“5-3”，图形表征方式可以是5个图形整体圈去3个，实物表征可以是5个学具中拿去3个，当然也可以用文字等形式来表征。学生能否用多种方式表征，与学生的理解程度存在正相关。在教学时，特别是在解决问题的过程中，运用不同的表征才能真正加深学生对数学的理解，更好地提升数学思维能力。教师可以在教学中有意识地设计一些信息较多且相互之间关系较为复杂的问题，让学生经历并体会到运用数学多元表征的丰富性和必要性，在这个过程中逐步梳理数学信息、对象之间的关系，促进学生对意义的内化、理解。

《义务教育数学课程标准（2011 年版）》指出：“教学应该以学生的认知发展水平和已有的知识经验为基础，面向全体学生，注重启发式和因材施教。”对一年级学生进行减法概念理解的调查正是基于这样的思考，让学生在减法意义、模型建构中借助丰富的现实情境，经历从具体情境到抽象算式的归纳过程，并能从算式中联想到具体情境，深刻感知减法不同形式的表达；最后，让学生通过语言表述、符号表征和算式表达等方式进行融会贯通，便于整体性、立体化理解减法的本质意义。