Menger PM-空间中循环R-压缩映射的不动点定理

刘孟递，吴照奇，朱传喜

(南昌大学数学系，江西 南昌 330031)

1 引言与预备知识

Menger在20世纪40年代引入了概率度量空间(简称PM-空间)的概念，为概率分析[1-2]这一新分支奠定了基础。此后很多学者致力于研究概率度量空间理论，并且试图应用它来解决其他的数学问题[3-6]。随着研究的深入，关于Menger PM-空间中非线性算子的不动点问题研究在近年来取得了丰富的成果[7-17]。

首先回顾Menger PM-空间中的一些基本概念和性质。

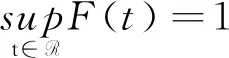
记D为一切分布函数全体所组成集合，H表示如下特定的分布函数：

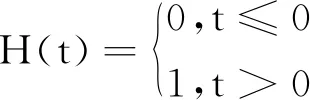
定义1.1[6]若映射满足以下条件：Δ:[0,1]×[0,1]→[0,1]满足以下条件：

(Δ-1)Δ(a,1)=a;

(Δ-2)Δ(a,b)=Δ(b,a);

(Δ-3)Δ(a,c)≥Δ(b,d),∀a≥b,c≥d;

(Δ-4)Δ(a,Δ(b,c))=Δ(Δ(a,b),c)。

则Δ称为三角范数(简称t-范数)。

t-范数的典型例子是Δmin，定义为Δmin(a,b)=min{a,b}，对一切a,b∈[0,1]。

定义1.2[6]若X是非空集，Δ是t-范数，F是从X×X到D的映射，且满足(记F(x,y)为Fx,y)：

(PM-1)Fx,y(0)=0;

(PM-2)Fx,y(t)=H(t),∀t∈R当且仅当x=y;

(PM-3)Fx,y(t)=Fy,x(t),∀t∈R;

(PM-4)Fx,y(t+s)≥Δ(Fx,z(t),Fz,y(s))对一切x,y,z∈X和t,s≥0成立。

则称三元组(X,F,Δ)为Menger概率度量空间(简称Menger PM-空间)。

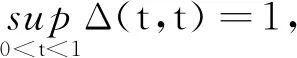
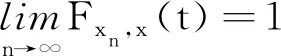
在本文中，Pcl(X),N,N0,R和R+分别表示Menger PM-空间(X,F,Δ)的非空τ-闭子集全体所成集合、正整数集、非负整数集、实数集和正实数集。

Boyd和Wong在文[18]中引入了如下函数类的概念。

定义1.3[18]若函数φ:[0,+∞)→[0,+∞)是右上半连续函数且φ(t)0成立，则称φ是Boyd-Wong函数。

对于X上的自映射f，若对一切x,y∈X及t>0，有Ffx,fy(t)≥Fx,y(φ(t))，其中φ是Boyd-Wong函数，则称f是Boyd-Wong压缩。

Khojasteh等人在文[19]中引入了模拟函数的概念，Shahzad等人为了便于验证Boyd-Wong函数是模拟函数，在文[20]中改进了模拟函数的概念。同时，文[20]也引入了如下的R-函数的概念。下面，我们将R-函数的概念推广到Menger PM-空间中。

定义1.4设A⊂R为一非空集，如果函数ρ:A×A→R满足如下两个条件：

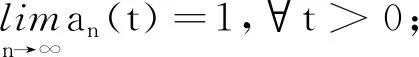
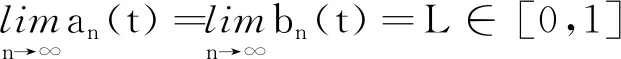
则称ρ是R-函数。

此外，Abbas等人在文[21]中给出了度量空间中R-压缩的概念，我们将其推广到Menger PM-空间中。

定义1.5[21]设(X,F,Δ)是Menger PM-空间，f是X上的自映射，如果存在ρ∈RA使得ran(F)⊂A和ρ(Ffx,fy(t),Fx,y(t))>0对一切x,y∈X且x≠y成立，其中RA是满足条件(ρ1)和(ρ2)的函数ρ:A×A→R的全体构成的集合，ran(F)是F的值域，定义为ran(F)={Fx,y(t):x,y∈X且t>0}⊂[0,1]，则称f是R-压缩。

Kirk在文[22]中给出了如下定义。

定义1.6[22]设X是非空集，p是正整数，f是X上的自映射。如果{Bi:i=1,2,…,p}是X中的有限个非空子集构成的集合，使得

f(B1)⊂B2,f(B2)⊂B3,…,f(Bp-1)⊂Bp,f(Bp)⊂B1,

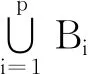
Kirk[22]等人在度量空间中引入了循环φ-压缩的概念。我们现在将其推广到Menger PM-空间中。

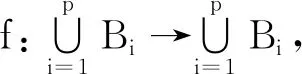
受上述定义启发，我们给出如下Menger PM-空间中循环R-压缩的概念，它是文[21]中定义1.15(考虑的是度量空间)的推广。

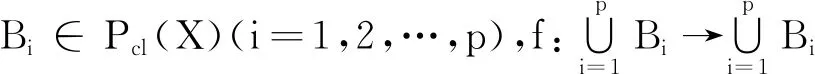
(ⅰ)存在ρ∈RA,ran(F)⊂A；

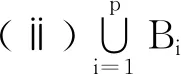
(ⅲ)ρ(Ffx,fy(t),Fx,y(t))>0，对一切x∈Bi,y∈Bi+1,x≠y,1≤i≤p成立，其中Bp+1=B1。

则称f是循环R-压缩。

借助于这一概念，本文将证明Menger PM-空间关于循环R-压缩的新的不动点定理，这一结果是文[21]及其他相关文献中定理的推广，并且丰富了Menger PM-空间中循环压缩映射的不动点理论。

2 主要结果

在本节中，我们给出Menger PM-空间中关于循环R-压缩的一个新的不动点定理。

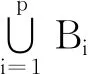
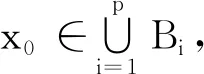
ρ(Ffxn-1,fxn(t),Fxn-1,xn(t))=ρ(Fxn,xn+1(t),Fxn-1,xn(t))>0,∀n∈N，

由R-函数的性质(ρ1)，有

(2.1)

下证{xn}是τ-柯西列。用反证法，假若不然，则存在ε0>0和λ0∈(0,1]，使得对一切k∈N，存在两个子列{xmk}和{xnk}(nk≥mk≥k)满足

Fxmk,xnk(ε0)≤1-λ0

不失一般性，可假定nk是确保上式成立并且大于mk的最小整数。选取jk∈{1,2,…,p}使得nk≥mk≥mk-jk且nk属于mk-jk+1的剩余类。则xmk-jk和xnk在不同的相邻集Bi和Bi+1中，其中i∈{1,2,…,p}。于是有

Fxmk-jk,xnk(ε0)≤1-λ0且Fxmk-jk,xnk-2(ε0)>1-λ0,∀k∈N

(2.2)

对于任意满足δ1+δ2<ε0的δ1,δ2∈(0,ε0)，有

Fxmk-jk,xnk(ε0)≥Δ(Fxmk-jk,xnk-2(ε0-δ1-δ2),Δ(Fxnk-2,xnk-1(δ1),Fxnk-1,xnk(δ2)))

(2.3)

令k→∞，由(2.1)式，可得

令δ1,δ2→0，由分布函数的左连续性和(2.2)式，可得

和

由此可得

(2.4)

类似地，对于任意满足δ1+δ2<ε0的δ1,δ2∈(0,ε0)，有

Fxmk-jk,xnk(ε0)≥Δ(Fxmk-jk,xmk-jk-1(δ1),

Δ(Fxmk-jk-1,xnk-1(ε0-δ1-δ2),Fxnk-1,xnk(δ2)))

(2.5)

和

Fxmk-jk-1,xnk-1(ε0)≥Δ(Fxmk-jk-1,xmk-jk(δ1),Δ(Fxmk-jk,xnk(ε0-δ1-δ2),Fxnk,xmk-1(δ2)))

(2.6)

在(2.5)式和(2.6)式中，令k→∞，由(2.1)式和(2.4)式以及分布函数的左连续性，可得

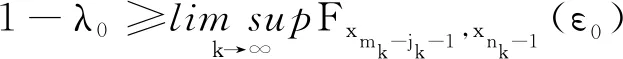
由上式可得

(2.7)

结合(2.2)式，(2.4)式和(2.7)式，可得

ρ(Ffxmk-jk-1,fxnk-1(ε0),Fxmk-jk-1,xnk-1(ε0))=

ρ(Fxmk-jk,xnk(ε0),Fxmk-jk-1,xnk-1(ε0))>0

由R-函数的性质(ρ2)，可得1-λ0=1，即λ0=0，这与条件λ0>0矛盾。因此，{xn}是(X,F,Δ)中的τ-柯西列。

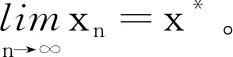
固定i∈{1,2,…,p}，使得x*∈Bi和fx*∈Bi+1。由上述证明过程，可选取序列{xn}的子列{xnj}，使得xnj∈Bi-1。因此

ρ(Ffx*,fxnj(t),Fx*,xnj(t))=

ρ(Ffx*,xnj+1(t),Fx*,xnj(t))>0,∀j∈N

由R-函数的性质(ρ2)，可得

(2.8)

注意到

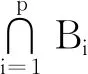
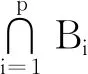
ρ(Ffx*,fy*(t),Fx*,y*(t))>0

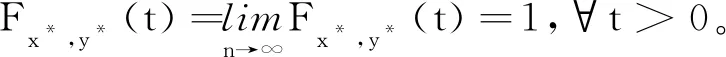
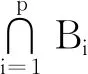
3 例子

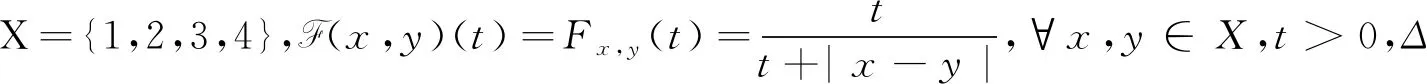
f1=f2=4,f3=f4=3

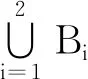
又定义ρ:[0,1]×[0,1]→R为

则ρ∈RA，即ρ是R-函数。事实上，设{an(t)}⊂(0,1]，使得ρ(an+1(t),an(t))>0，∀n∈N,t>0成立，则an+1(t)>an(t)，且

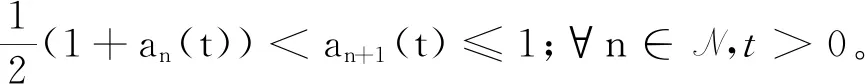
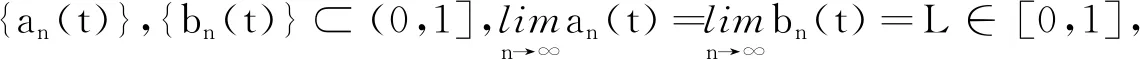
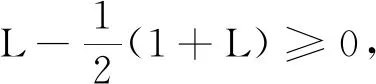
进一步地，容易验证ρ(Ffx,fy(t),Fx,y(t))>0,∀x∈B1,y∈B2,x≠y及t>0成立，且ρ(Ffx,fy(t),Fx,y(t))>0,∀x∈B2,y∈B1,x≠y及t>0成立。