凸轮焊检尺在锐角焊缝测量中的研究

山东核电设备制造有限公司，山东 烟台 265118

1 锐角焊缝测量中存在的问题

1.1 扇形凸轮尺无法接触工件表面问题

由于尺身高度原因，扇形凸轮尺无法接触工件表面进行测量（见图1）。在尺身高度能够接触到高度方向工件表面的情况下，通过建立数学模型进行分析，首先论证锐角焊缝中存在一个测量角度极限，然后计算出该极限角度。为求证焊检尺极限角度及大小，根据焊检尺固有尺寸（见图2），建立数学模型（见图3）。从图2、图3中可以看出，当α＞β时，AC=BC´=b为尺身高度，AA´=BB´=FF´=a，DA´=D´B´=c，CD=C´D´等为尺子自身固有尺寸，DE=r为凸轮尺半径，DE⊥OC，D´E´⊥OC´，证明α为极限角度。

图1 无法接触

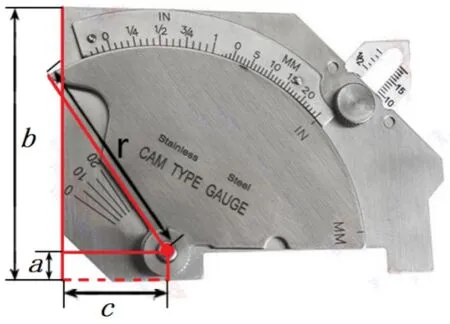
图2 焊检尺固有尺寸

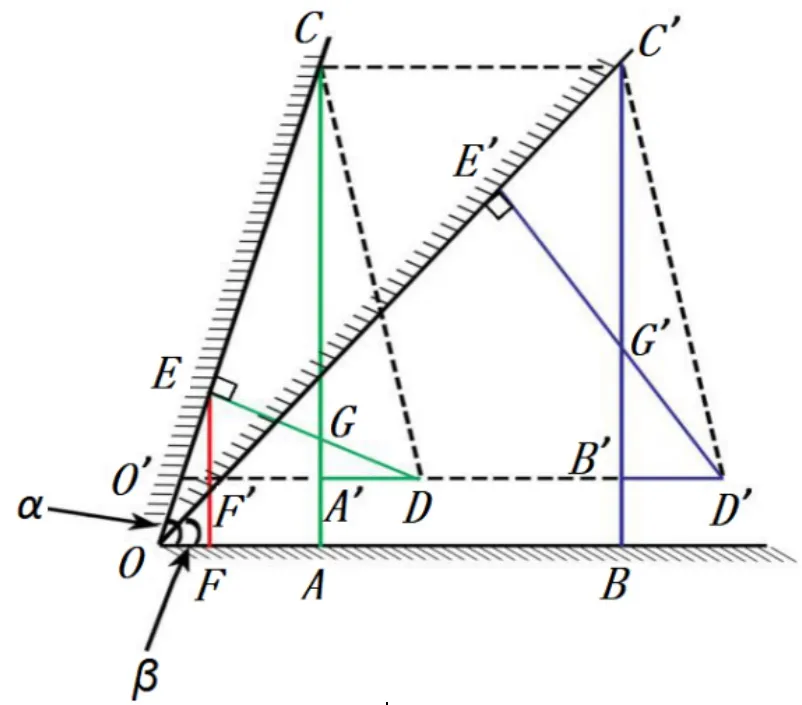
图3 焊检尺不同角度下的数学模型

（1）根据数学平面几何原理及三角函数，可得下式：

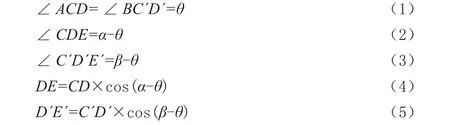
根据已知条件（α＞β，CD=C´D´）以及余弦函数在0°～90°内为递减函数，DE＜D´E´，即在β角度时，凸轮尺远离工件表面；反之，可知凸轮尺深入工件内部，因此存在测量的极限角度α。

（2）根据三角函数关系，可得下式：

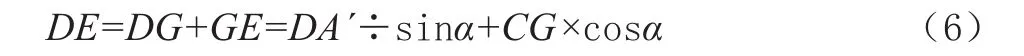
将CG=AC-AA´-GA´代入上式，可得角度与凸轮半径关系式如下：

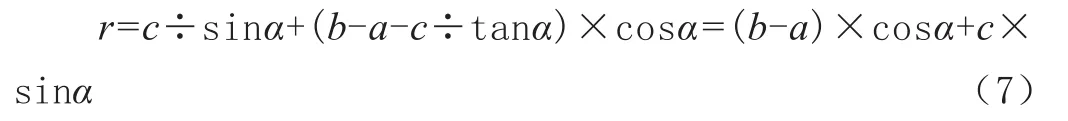
设 cosα=X，根据三角函数常用公式 sinα2+cosα2=1，将a=6.35、b=69.85、c=25.4、r=50.8（单位为mm）代入关系式，得出一元二次方程：

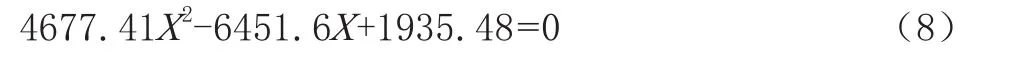
解得X1≈0.93，即α趋于0，与实际不符，应舍去；X2≈0.44，即α向下取整，取63°。

综上所述，焊检尺可测量的极限角度为α=63°。

1.2 扇形凸轮尺无法测量焊脚尺寸问题

因焊脚尺寸原因，扇形尺无法测量焊脚尺寸（见图4）。当工件角度保持不变时，在可测量范围，焊检尺越接近焊缝，理论上测点位置越往上走，测量数值越大；焊检尺越远离焊缝，理论上测点位置越往下走，测量数值越小；当扇形凸轮尺旋转圆心与工件接触点连线垂直工件表面时，测量数值最小。测量范围数学模型见图5。

图4 无法测量

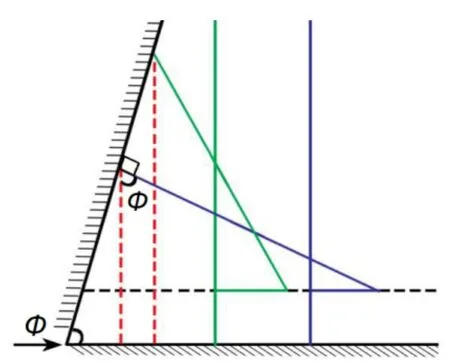
图5 测量范围内的数学模型

由图3可知，焊脚尺寸h计算公式为

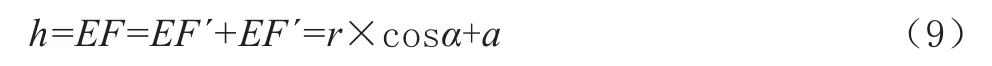
由图5可知，在可测量的锐角范围内，焊检尺可测量的最小值公式为

焊检尺可测量的最小焊脚尺寸与工件角度存在相关性，随着φ的减少，焊检尺可测量的最小焊脚尺寸逐渐增大。

2 结论的适用性修正

对于最小值公式，当φ趋近于90°时，hmin趋近于6.35，在直角焊缝时，焊检尺能够测量的最小焊脚尺寸为6.35mm，明显与实际情况相违背。通过实践与分析，发现模型的建立是基于接触倾斜的工件表面，而锐角焊缝顶部焊趾存在一定的厚度，实际测量接触部位是焊缝顶部焊趾，因此最小焊脚尺寸公式需要进行适用性修正。根据直角焊缝焊脚尺寸测量为0～25mm（见图6），计算出零位测量点与工件表面偏离距离ΔL：

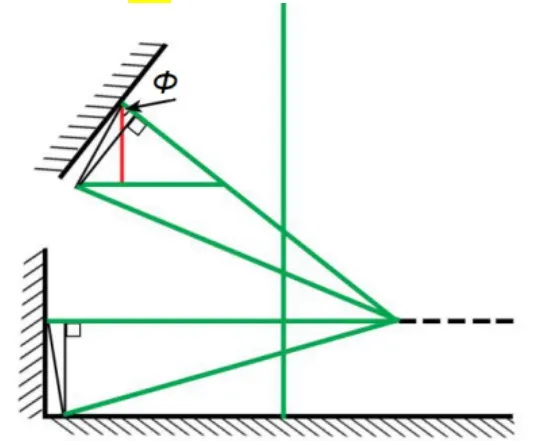
图6 测量范围修正模型

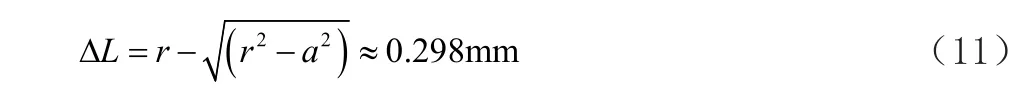
在实际测量中此微小偏离量可以忽略不计。在φ角度的锐角中焊检尺圆弧切线偏离与直角时相同，即所形成的两个三角形是相等，从而得出锐角φ时两点高度差公式如下：

修正后公式如下：

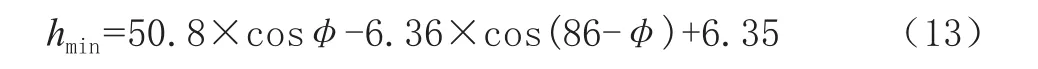
3 实际应用意义

为了方便使用，利用修正后的公式，结合焊检尺测量焊脚尺寸精度（±0.5mm）测算出结果，见表1。

表1 锐角与焊脚尺寸对应表

在产品质量检查中，对于锐角焊缝以往常采用参考线法进行间接计算测量。对于范围以内产品角焊缝，参照表1，能够准确地编制检查工艺文件，减少焊前检查的标记环节，方便现场焊接检验，从而达到精细化施工和检验的目的。