声波夹带法测量可吸入颗粒物粒径的误差和范围
杨旭峰, 凡凤仙
(上海理工大学 能源与动力工程学院,上海 200093)
声波夹带法测量可吸入颗粒物粒径的误差和范围
杨旭峰,凡凤仙
(上海理工大学 能源与动力工程学院,上海 200093)
摘要:基于同时考虑Stokes力和非稳定力的水平驻波声场中的颗粒动力学模型,通过数值模拟计算研究声波夹带法测量粒径的误差和范围.结果表明:对于特定粒径的颗粒,存在一个使测量误差为0的最佳测试声场频率,低于该频率,粒径测量值偏大,高于该频率,粒径测量值偏小;随着颗粒密度的增加,测量误差迅速减小,最终测量误差接近0;随着声波频率的增加,测量范围的上限和下限均下降,粒径测量范围减小;随着声强的增加,测量范围上限增大,下限则保持不变,粒径测量范围增大.
关键词:粒径测量; 声波夹带法; 可吸入颗粒物; 测量误差; 测量范围
目前,颗粒物污染已成为我国突出的大气环境问题,这些颗粒物主要来源于火力发电、交通运输和工业部门的排放.其中,粒径在10 μm以下的可吸入颗粒物(PM10)易于吸附空气中的有害物质,并能够进入人体呼吸系统,给国民健康带来严重威胁[1-3].除尘器的工作效率和颗粒物的危害性均与颗粒粒径密切相关.因此,对颗粒进行精确的粒径测量对于颗粒物污染防治有着重要意义.此外,微米级颗粒同样存在于其他领域,如制药、水泥、化工等的造粒过程中,为确保产品质量,也需要对颗粒粒径进行精确测量.
常规的单颗粒粒径测量方法,如显微镜成像法、沉降法和光散射法等,均难以快速、精确地获得微米颗粒的尺寸[4-5].与这些方法相比,声波夹带法能获取细微颗粒的粒径,且测量时无需标定,测量过程迅速,是一种具有研究价值的单颗粒粒径测量方法[6],其在可吸入颗粒物污染防治和微米尺度颗粒造粒领域具有应用潜力.该方法借助高速显微摄像系统获得声波作用下颗粒的运动图像,并基于颗粒在声场中的夹带运动方程推演出颗粒粒径.
夹带运动是颗粒在声场中最基本的运动特性.2006年,姚刚等[7]对颗粒粒径表达式进行了理论推导,提出利用声场中可吸入颗粒物的夹带宽度和沉降距离测量单个可吸入颗粒物粒径的方法,并进行了驻波声场中的粒径测量实验.这种方法的理论推导过程中只考虑了Stokes力和重力作用,而忽略了颗粒在非均匀流场中受到的Basset力、压力梯度力、虚拟质量力等非稳定力的作用.随着对声场中颗粒动力学特性研究的逐步深入,非稳定力对颗粒夹带运动的影响逐渐受到关注.2012年,Cleckler等[8]给出了声场中颗粒受Stokes力和非稳定力作用下的无量纲运动方程,研究发现能否忽略非稳定力取决于颗粒与气体的密度比ε以及无量纲弛豫时间ωτ(ω为声波角频率,τ为颗粒弛豫时间)的大小.由于非稳定力的影响,用现有的声波夹带法来测量可吸入颗粒物粒径存在一定的误差.此外,特定颗粒的夹带宽度取决于声强和频率.对于给定的声场,当颗粒自身大小与夹带宽度相比不能忽略时,将造成较大的夹带宽度测量误差,从而影响粒径测量的准确性;当夹带宽度接近于声场中气体介质的振动宽度时,夹带宽度对粒径的变化很不敏感,也不利于颗粒粒径的精确测量.因此,给定的声场将对应于一定的粒径测量范围.
鉴于此,笔者建立同时考虑Stokes力和非稳定力的驻波声场中颗粒动力学模型,通过数值模拟方法研究声波夹带法测定颗粒粒径的误差和测量范围,为声波夹带法测量单颗粒粒径的优化提供理论基础和指导方法.
1数学模型
1.1驻波声场波动方程
由Navier-Stokes方程可推导出驻波声场的波动方程[9]为:
ug,x(x,t)=uasin(kx)cos(ωt)
(1)
式中:ug,x为声波引起的气体介质振动速度;x为位置坐标;t为时间;ua为速度振幅;k为波数,k=ω/c,ω=2πf,c为声速,f为声波频率.
通常采用声压级来描述声强,其表达式为:
(2)
式中:L为声压级;pr为参考声压,pr=2×10-5Pa;ps为声压有效值.
(3)
式中:ρg为气体密度.
1.2颗粒动力学模型
处于声场中的颗粒在水平方向(x方向)上将受到Stokes力、Basset力、压力梯度力和虚拟质量力的作用,其运动方程可表示为:
(4)
式中:mp为颗粒质量;up,x为颗粒速度的水平分量;Fst为Stokes力;Fb为Basset力;Fp为压力梯度力;Fvm为虚拟质量力.
Stokes力的表达式[10]为:
(5)
式中:μg为气体动力黏度;dp为颗粒粒径;Cc为Cunningham修正系数.
Cc=1+Kn[1.257+0.4×exp(-1.1/Kn)]
(6)
式中:Kn=2λg/dp,为克努森数,其中λg为气体分子平均自由程.
Basset力、压力梯度力、虚拟质量力的表达式[11-13]分别为:
(7)
(8)
(9)
式中:t′为积分变量.
1.3声波夹带法测量颗粒粒径的依据
姚刚等[7]基于声波夹带法测量颗粒粒径时认为,位于水平驻波声场中的颗粒水平方向上仅在Stokes力作用下随声波在平衡位置往复振动,即发生夹带运动;在竖直方向上受到Stokes力和重力的共同作用,二力平衡后,颗粒将以恒定的速度沉降.
在水平方向上,颗粒夹带宽度Xp和空气质点振动宽度X0的比值[7]可表示为:
(10)
式中:η为夹带系数;ρp为颗粒密度.
在竖直方向上,极短时间(t=3τ)内颗粒运动速度即可达到终端沉降速度,此后颗粒做匀速运动.弛豫时间τ和沉降距离Yp的表达式[14]分别为:
(11)
(12)
式中:g为重力加速度.
联立式(10)和式(12)消去Cc,可得到颗粒粒径的表达式:
(13)
由式(13)可知,在颗粒密度、声波频率、空气动力黏度、空气质点振动宽度已知的情况下,如果能测得时间t内颗粒夹带宽度和沉降距离,就能确定颗粒粒径.
1.4计算方法
采用变步长四阶Runge-Kutta算法对颗粒运动方程进行求解.其中,Basset力通过将气体速度和颗粒速度基于经历的时间步进行离散而计算得到,即
(14)
式中:n为颗粒运动经历的时间步数;Δug,xi和Δup,xi分别为第i个时间步内气体速度和颗粒速度增量;i为时间步数,i=1,2,…,n;t0为第1个时间步的起始时间;ti为第i个时间步的终止时间.
颗粒的运动轨迹可由各时间步长内颗粒的位移叠加获得.根据二阶隐式Adams插值算法,颗粒在声波传播方向的位移为
(15)
式中:xp为位移;Δt为时间步长.
2不同密度比下的夹带系数
为说明非稳定力对颗粒夹带运动的影响,图1给出了不同密度比(ε=ρp/ρg)情况下,考虑非稳定力以及仅考虑Stokes力时夹带系数的对比关系.由图1可知,ωτ≤1时,4种计算情况下的曲线几乎完全重合,这表明此时非稳定力对计算结果的影响可以忽略;当ωτ>1时,随着ωτ的增加,有、无非稳定力情况下夹带系数计算结果的差别趋于明显,并且不同密度比下颗粒的夹带系数也有差别,如ωτ=5时,仅考虑Stokes力时的夹带系数相对于考虑了非稳定力且ε=2 000和ε=500时的夹带系数的偏差分别为8.62%和10.65%.由图1还可以看出,对于特定的颗粒,随着声波频率的增加,夹带系数先是接近于1,接着急剧减小,最后夹带系数的变化又趋于平缓.在声波夹带法测量颗粒粒径过程中,通过高速显微摄像系统获得颗粒的夹带宽度,当测量粒径所依据的夹带系数接近于1或者0时,微小的夹带宽度变化将带来较大的粒径变化,给粒径测量带来较大误差.为减小这种测量误差,选取0.1≤η≤0.9为宜.由于夹带系数主要由声波频率决定,因而一定频率的声场对应于一定的测量范围.另外,在频率给定的情况下,颗粒的夹带宽度随声强的增加而增大,如果采用的声强过小,会引起颗粒夹带宽度过小,此时颗粒粒径对颗粒夹带宽度的干扰较强,对测量结果的准确性带来不利影响;如果声强过大,声源的成本和能耗将增加.为兼顾测量的准确性和测量装置的成本,夹带宽度Xp满足10dp≤Xp≤100dp为宜.可见,声波夹带法测量颗粒粒径时,不同强度的声场也对应于不同的粒径测量范围.
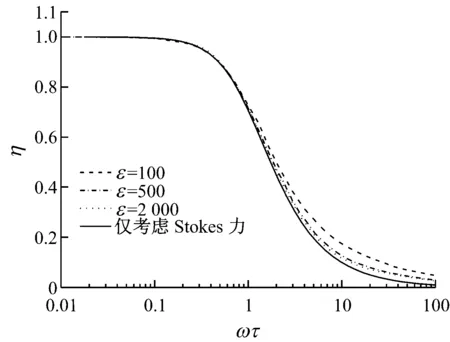
图1 夹带系数随无量纲弛豫时间的变化
3粒径测量误差和测量范围分析
在气体静压p=101 325 Pa、温度T=300 K、颗粒初始位置横坐标x0=3λ/4的条件下,对声波夹带法测量可吸入颗粒物粒径的误差和范围进行数值分析.
3.1忽略非稳定力引起的测量误差分析
3.1.1声波频率对测量误差的影响
图2给出了ε=2 000时,颗粒粒径dp为1 μm、2 μm、3 μm和4 μm情况下,声波夹带法测量颗粒粒径的相对误差随声波频率的变化关系.图中,以测量颗粒粒径的相对误差Δdp来表征测量误差,Δdp=(dp1-dp)/dp,其中,dp1为粒径的测量值.由图2可知,当dp=1 μm时,在声波频率为300~20 000 Hz时,测量值始终偏大,测量误差随声波频率的增大而减小;对于dp为2 μm、3 μm和4 μm的颗粒,随着声波频率的增大,测量值先偏大、后偏小,在声波频率分别为4 598 Hz、2 145 Hz和1 210 Hz时,测量值与真实值相同.这表明对于特定粒径的颗粒,存在一个使测量误差为0的最佳测试声波频率,低于该频率,粒径测量值偏大;高于该频率,粒径测量值偏小;越接近该频率,测量越精确.
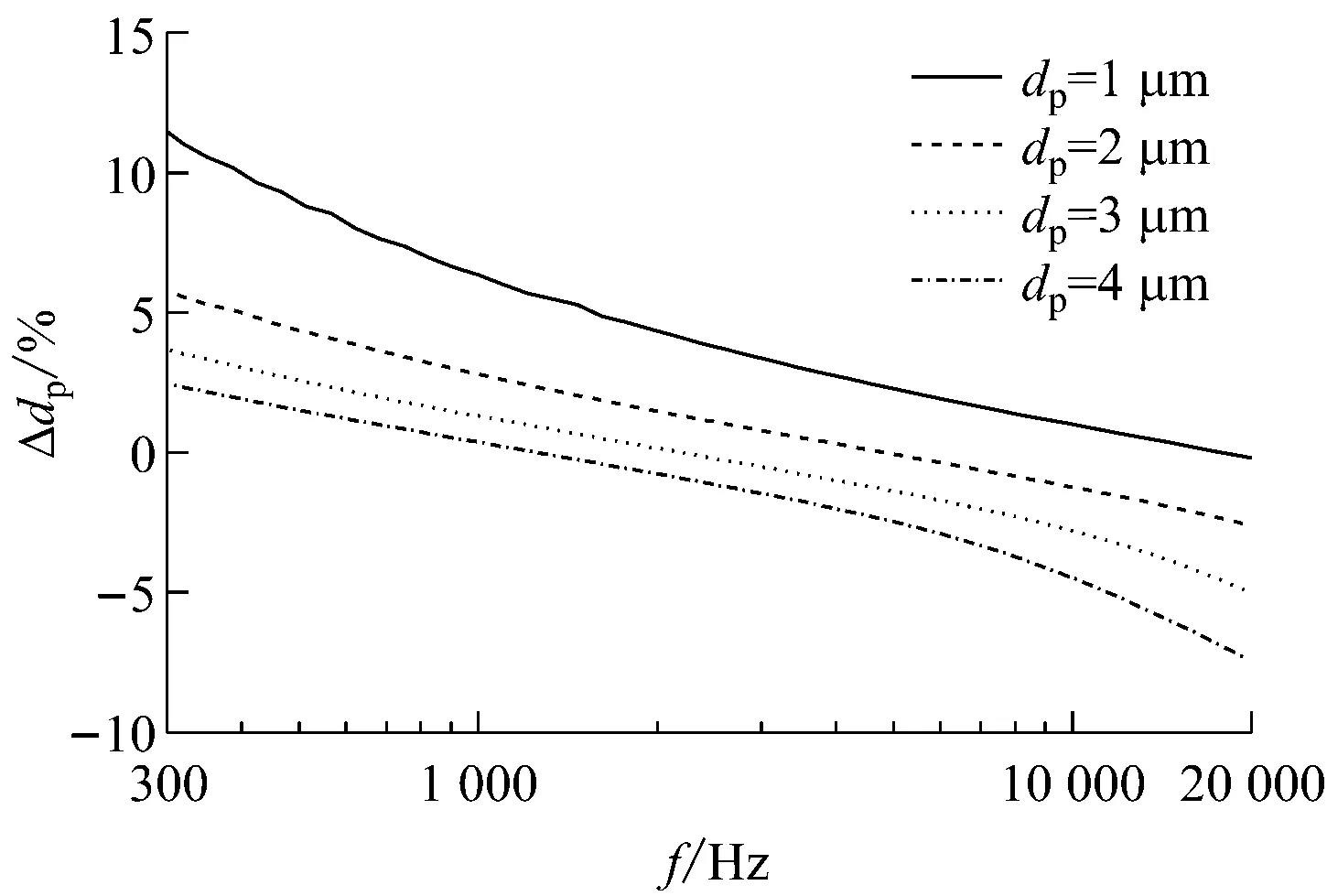
图2 测量误差随声波频率的变化
3.1.2密度比对测量误差的影响
图3给出了声波频率f=2 000 Hz,颗粒粒径dp为1 μm、2 μm、3 μm和4 μm条件下,声波夹带法测量颗粒粒径的测量误差随密度比的变化关系.由图3可知,随着密度比的增加,测量误差先迅速减小,而后减小速度趋缓,直至测量误差几乎保持不变.当dp为1 μm和2 μm时,粒径测量值偏大;当dp为3 μm和4 μm时,测量误差在ε=2 000时即接近于0.从图3还可以看出,对于相同密度比的颗粒,采用同样的测试声场时,颗粒粒径越大,对应的测量误差越小.

图3 测量误差随密度比的变化
3.2粒径测量范围分析
为减小测量误差,同时兼顾测量装置成本,在忽略非稳定力引起的相对误差Δdp≤5%,且0.1≤η≤0.9、10dp≤Xp≤100dp条件下,研究声波频率和声强对粒径测量范围的影响.
3.2.1声波频率对粒径测量范围的影响
图4给出了ε=2 000、L=140 dB时,粒径测量范围随声波频率的变化关系.其中,dpmax为粒径测量上限,dpmin为粒径测量下限.由图4可知,随着声波频率的增加,颗粒粒径测量上限和下限均降低,相对于测量下限,上限的下降程度更为显著,导致粒径测量范围缩小.下限粒径对应的颗粒由于具有更小的惯性而具有更好的跟随性,其夹带系数受声波频率的影响较弱,颗粒夹带宽度能够保持在适宜的范围内,因此下限粒径对声波频率变化的敏感性较弱;而惯性较大的粒径测量上限对应的颗粒跟随性较差,声波频率对其夹带系数和夹带宽度有重要影响,使得粒径测量上限受声波频率变化的影响显著.
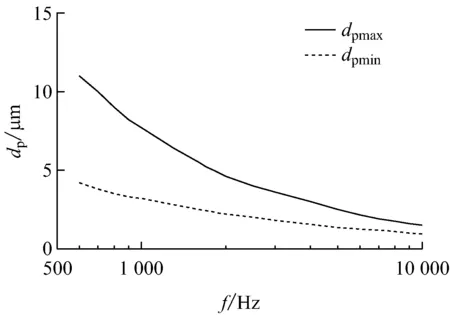
图4 粒径测量范围随声波频率的变化
3.2.2声强对粒径测量范围的影响
图5给出了ε=2 000、f=3 000 Hz时,颗粒粒径测量范围随声强的变化关系.由图5可知,随着声强的增加,粒径测量上限增大,粒径测量下限则保持不变,使得粒径测量范围增大.同一颗粒的夹带系数不受声强的影响,而夹带位移随声强的增加而增大.在声波频率为3 000 Hz、声强为125~150 dB时,数值模拟结果表明,颗粒粒径测量上限由颗粒夹带宽度确定,即dpmax=Xp/10;粒径测量下限由夹带系数确定,即dpmin为η=0.9时对应的颗粒粒径.由于一定声波频率下的颗粒夹带宽度取决于声强,随着声强的增加,颗粒夹带宽度增大,粒径测量上限随之增大;同时,由于夹带系数不受声强的影响,因而粒径测量下限不随声强而变化.
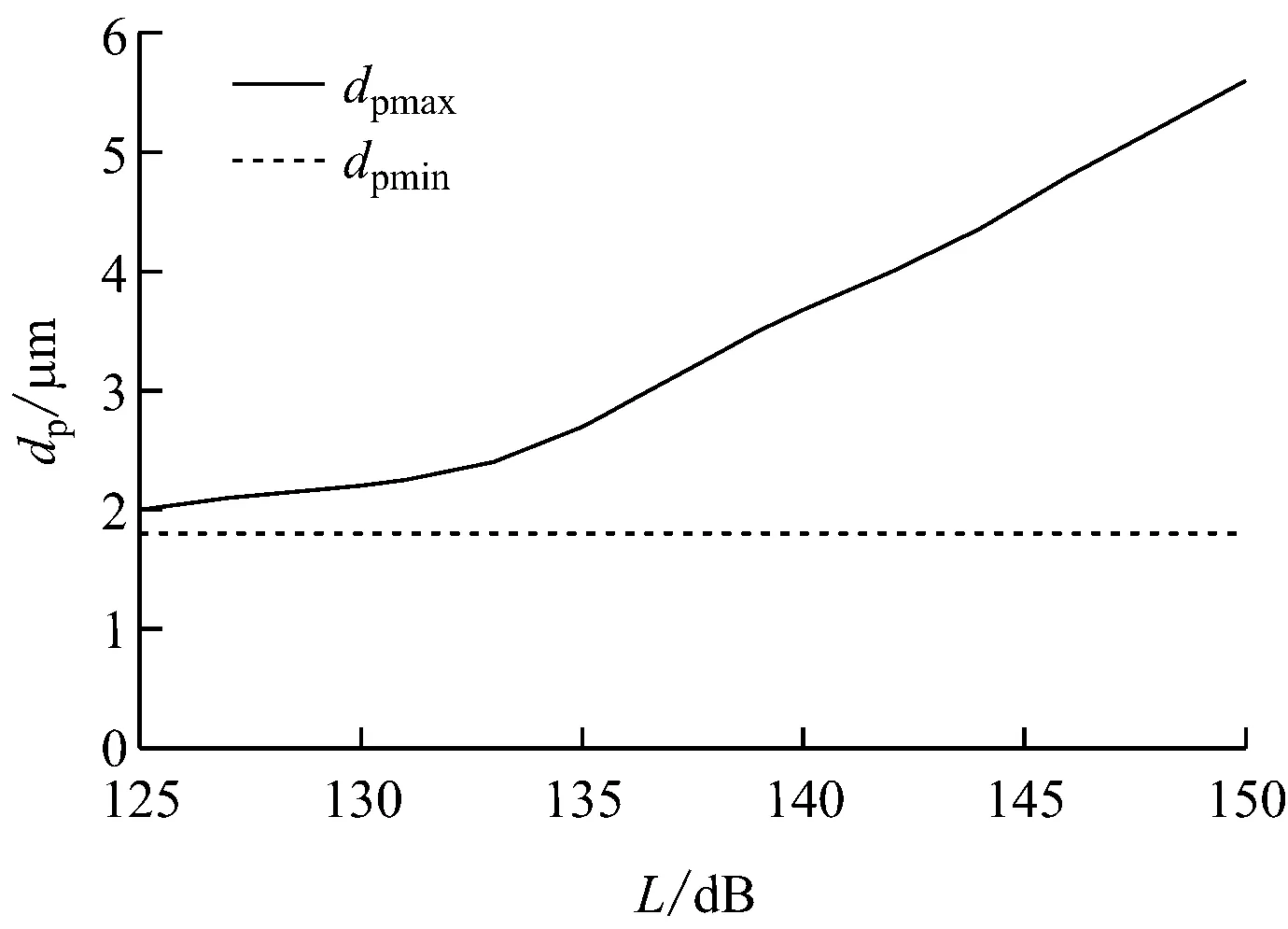
图5 粒径测量范围随声强的变化
4结论
(1)对于特定粒径的颗粒,存在一个使测量误差为0的最佳测试声场频率,低于该频率,粒径测量值偏大;高于该频率,粒径测量值偏小.
(2)随着颗粒密度比的增加,测量误差迅速减小,最终接近于0;对于相同密度比的颗粒,粒径越大,测量误差越小.
(3)随着声波频率的增加,颗粒粒径测量范围的测量上限和下限均下降,但是上限下降更为迅速,使得粒径测量范围随声波频率的增加而减小.
(4)随着声强的增加,颗粒粒径测量范围上限增大,下限则保持不变,使得粒径测量范围随声强的增加而增大.
参考文献:
[1]WEN Chang, XU Minghou, YU Dunxi,etal. PM10formation during the combustion of N2-char and CO2-char of Chinese coals [J]. Proceedings of the Combustion Institute,2013, 34(2): 2383-2392.
[2]ZHANG L W, CHEN X, XUE X D,etal. Long-term exposure to high particulate matter pollution and cardiovascular mortality: a 12-year cohort study in four cities in northern China[J]. Environment International, 2014, 62: 41-47.
[3]李敬伟,施浩勋,李敏,等.燃煤电厂飞灰PM2.5及PM2.5-10中多环芳烃分布特性研究[J]. 动力工程学报,2015,35(4): 306-311.
LI Jingwei, SHI Haoxun, LI Min,etal. Distribution of polycyclic aromatic hydrocarbons in PM2.5and PM2.5-10from fly ash of coal-fired power plants[J]. Journal of Chinese Society of Power Engineering, 2015, 35(4): 306-311.
[4]YOSHIDA H, MASUDA H, FUKUI K,etal. Particle size measurement with an improved sedimentation balance method and microscopic method together with computer simulation of necessary sample size[J]. Advanced Powder Technology,2001,12(1): 79-94.
[5]邵鸿飞,柴娟,黄辉.粒度分析及粒度标准物质研究进展[J]. 化学分析计量, 2012,21(2): 99-101.
SHAO Hongfei, CHAI Juan, HUANG Hui. Research progress of particle size analysis and particle size standard reference material [J]. Chemical Analysis and Meterage, 2012,21(2): 99-101.
[6]COLE R, TENNAL K B. Acoustic measurement of aerosol particles [J]. Aerosol Science and Technology, 1993, 19(3):339-350.
[7]姚刚,赵兵,杨林军,等.可吸入颗粒粒径声学夹带法测量的实验研究[J]. 热能动力工程, 2006,21 (3): 267-269.
YAO Gang, ZHAO Bing, YANG Linjun,etal. Experimental study of the measurement of inhalable particle diameter by the use of an acoustic entrainment method[J]. Journal of Engineering for Thermal Energy and Power, 2006,21 (3): 267-269.
[8]CLECKLER J, ELGHOBASHI S, LIU F. On the motion of inertial particles by sound waves[J]. Physics of Fluids, 2012, 24(3): 033301.
[9]BRUNEAU M. Fundamentals of acoustics [M].London: ISTE Ltd,2006:636.
[10]NAKAJIMA Y, SATO T. Electrostatic collection of submicron particles with the aid of electrostatic agglomeration promoted by particle vibration[J]. Powder Technology, 2003,135/136:266-284.
[11]ROSTAMI M, ARDESHIR A, AHMADI G,etal. On the effect of gravitational and hydrodynamic forces on particle motion in a quiescent fluid at high particle Reynolds numbers[J]. Canadian Journal of Physics, 2008, 86(6):791-799.
[12]WANG B, YU A B. Computational investigation of the mechanisms of particle separation and "fish hook" phenomenon in hydrocyclones[J]. AIChE Journal, 2010, 56(7): 1703-1715.
[13]SIMCIK M, RUZICKA M C, DRAHOS J. Computing the added mass of dispersed particles[J]. Chemical Engineering Science, 2008, 63(18):4580-4595.
[14]DONG S, LIPKENS B, CAMERON T M. The effects of orthokinetic collision, acoustic wake, and gravity on acoustic agglomeration of polydisperse aerosols[J]. Journal of Aerosol Science, 2006, 37(4):540-553.
Error and Range in Measurement of Inhalable Particle Sizes by Acoustic Entrainment Method
YANGXufeng,FANFengxian
(School of Energy and Power Engineering, University of Shanghai for Science and Technology,Shanghai 200093, China)
Abstract:Based on the dynamic model for particles subjected to both the Strokes force and unsteady force in a horizontal standing wave acoustic field, the error and range in measurement of particle sizes by acoustic entrainment method were numerically studied. Results show that for a specified size of particles, there exists an optimal acoustic frequency corresponding to zero error of particle size measurement; when the acoustic frequency is lower or higher than the optimal one, the measured value would be accordingly larger or smaller than the true value. As the particle density increases, the measurement error decreases rapidly, and finally the error approaches to zero. Both the upper limit and lower limit of the measurement range reduce with the increase of acoustic frequency, resulting in decreased range of particle size measurement. As the acoustic intensity increases, the upper limit of the measurement range increases but the lower limit keeps constant, thus the measurement range increases.
Key words:particle size measurement; acoustic entrainment method; inhalable particle; measurement error; measurement range
文章编号:1674-7607(2016)03-0196-05
中图分类号:TB52+9
文献标志码:A学科分类号:470.10
作者简介:杨旭峰(1989-),男,湖北武汉人,硕士研究生,主要从事声场中颗粒动力学数值模拟方面的研究.
基金项目:国家自然科学基金资助项目(51206113,51176128)
收稿日期:2015-04-24
修订日期:2015-07-13
凡凤仙(通信作者),女,副教授,博士,电话(Tel.):13761377356;E-mail:fanfengxian@hotmail.com.

