热声不稳定主动控制的SVM时间序列预测模型

周　昊，　丁　芳，　黄　燕

(浙江大学 能源清洁利用国家重点实验室， 杭州 310027)



热声不稳定主动控制的SVM时间序列预测模型

周昊，丁芳，黄燕

(浙江大学 能源清洁利用国家重点实验室， 杭州 310027)

摘要：针对目前热声主动控制方法中存在的滞后问题，提出采用支持向量机算法进行热声振动时间序列的模糊预测.在自行设计的Rijke管热声不稳定实验台上进行扬声器扰动实验，采集热声振动动态压力序列，利用相空间重构法则构建输入输出数据集，并采用支持向量回归机建立预测模型，用测试集进行校验，定性分析了嵌入维数和延迟时间对时间序列预测精度的影响.结果表明：所用方法能得到较高的预测精度，模型在较高的延迟时间下仍能保持决定系数为0.95的高拟合度，验证了该时间序列预测方法的可行性.

关键词：热声振动； Rijke管； 时间序列； 支持向量机； 预测

热声不稳定是燃烧器工作时火焰面热释放脉动与燃烧室声场耦合形成的一种燃烧不稳定现象，是现代燃气轮机和航空发动机等设备采用贫燃预混燃烧技术时所碰到的常见问题.在设备工作过程中，燃烧器内部空间存在大振幅的压力振荡，并发出高分贝低频噪声，致使设备疲劳损伤，燃烧效率降低.其产生的机理为著名的瑞利准则[1]：当燃烧热释放脉动与燃烧室声场的相位一致时，燃烧室内的压力振荡被不断增强，最终形成持续的大振幅压力振荡.

热声振动的本质是热能与声能的耦合，在燃烧室内存在着热释放振动、传热传质、气体动力学及黏性损失等复杂的原理机制.由于热声振动具有高自由度、复杂的非线性耦合特性[2]，使得提出一个合理的热声预测模型和设计可靠的控制系统具有很大难度.国内外对热声不稳定控制的研究有2种思路：一是增进对热声不稳定现象的理解，改进燃烧器设计来增强燃烧稳定性[3]；二是放弃从细节上解释热声不稳定机理，直接增加主动控制系统来抑制燃烧不稳定[4]，如采用扬声器作为制动器干扰燃烧室中的声场[5].虽然扬声器受限于提供大功率振幅扰动，但由于其较好的频域响应特性而受到较多研究者的青睐，典型的闭环控制系统包括动态压力传感器、信号识别转换算法以及根据转换信号进行响应的扬声器[6].其中信号处理算法是闭环控制的一大难点，传统的传递函数算法采用即时采样并移相的方法，但由于作动器及电路的响应时间较长，其滞后效应削弱了控制作用.尽管也有很多闭环控制系统考虑到这一点，加装了时间延迟算法，但仍然存在问题，相当于作动器做出反应的对象是来自过去的热声振动时间序列，当声压采样端不稳定时，反馈控制系统会产生剧烈振荡[7].为了弥补典型扬声器闭环控制系统的缺陷，笔者提出采用模糊预测的方法对振动时间序列进行模拟，将预测的时间序列作为输入，削减滞后反应带来的误差.

国外学者对热声振动时间序列的模拟研究进行了一些尝试，Cammarata等[8]采用非线性自回归滑动平均(NARMAX)算法对火焰前沿热释放率、燃烧室内及室外振动压力的时间序列进行预测；Selimefendigil等[9]采用非线性自回归(NARX)神经网络识别对热释放模型进行模拟预测； Daley等[10]将神经网络时间序列预测模型加入到反馈控制系统中，用大气压力来演示该控制策略的可行性.笔者在自行搭建的Rijke型燃烧器上进行了扬声器扰动实验，并采用支持向量机对测得的压力数据进行时间序列的建模预测.

1支持向量机算法

支持向量机(SVM)是Cortes等[11]提出的一种新的机器学习算法，该算法建立在统计学习理论的VC维理论和结构风险最小原理基础上，有限的样本信息在模型的复杂性和学习能力之间寻求折衷，有效地避免了过学习和欠学习现象，获得良好的泛化能力.其主要的求解方法为：通过引入核函数将数据向高维Hilbert空间转化，使其线性可分，转换成一个凸二次规划问题，并用拉格朗日函数寻求全局最优解.

(1)

(2)

(3)

(4)

利用Langrange函数和Wolfe的对偶理论，并利用核函数在高维空间求解决策函数中的未知系数ω和b.

(5)

(6)

构造决策函数：

(7)

2扬声器扰动实验

2.1实验台简介

笔者自行设计的Rijke型燃烧器热声不稳定实验台架如图1所示.燃烧器为管长1 066 mm、内径40 mm、壁厚4 mm的不锈钢圆管，上端开口，下端封闭，致密堇青石材质的多孔介质火焰稳燃体位于燃烧器下端1/4管长处，上方安装电点火器，甲烷与空气在预混罐中完成混合后在稳燃体上方燃烧.在管子上方出口不远处悬挂扬声器作为扰动声源，扬声器通过P5000S功率放大器进行功率放大，由PC端进行频率和音量的控制.

在燃烧器的热源处采用CYG1406压力传感器进行声波测量，量程误差为0.5%，频率为20 kHz，安装在距Rijke管底部160 mm的高处，采用半无限法测量，即T形接口的外侧接5 m长的硅胶管，以避免声波的反射效应.压力传感器连接NI-6210数据采集卡进行数据传输，通过PC运行的LABVIEW后台程序进行高速、连续、实时数据采集，采样频率设置为25.6 kHz.实验中，通过Alicat流量计控制进气，设置甲烷体积流量为14.9 mL/s、空气体积流量为135 mL/s.调节扬声器的频率和声压级，共50个工况，采集燃烧室内的压力波动时间序列，其中频率和声压级由PC声控插件调节，频率为50～500 Hz，增量50 Hz，声压级开度为20%～100%，增量为20%，用声压测试计在扬声器端口平面正中心垂直上方50 mm处测量绝对声压级，其值在90～125 dB.

图1　Rijke型燃烧器热声不稳定实验台示意图

2.2压力波形曲线分析

图2为无扬声器扰动和300 Hz、100%开度扰动下的压力波形和频谱分析曲线.由于实验采集数据量庞大，图中仅呈现了振动稳定后达到极限周期的部分，连续采样频率为25 600 Hz，采样点充足，保证波形的平整性.由图2可知，在无扬声器扰动时，振动波形较为平稳，对其进行FFT分析，呈现出明显的单频振幅，峰值的频率为464 Hz，振幅为204 Pa.当扬声器扰动添加至燃烧室内的固有声场时，原有声场将被打乱，如图2(b)所示，压力波形呈现一定程度的毛刺，从频谱分析可以看出，主频仍维持在464 Hz，主频振幅峰值降到167 Pa，比无扬声器扰动时降低18.1%，同时也在300 Hz处激发出振幅为37 Pa的次频.对采样的50个工况进行压力波形和频谱的对比分析，不同扬声器频率对压力波形的扰动程度不同，扰动频率接近声场固有频率(即450 Hz)时的波形最为扭曲，相同频率时，声压级越大，扰动程度越大.扰动后的频谱分析中，主频频率位置不变，振幅呈现不同程度的衰减，变化范围为131～219 Pa，最大降幅为35.8%，也有出现负衰减的情况，这是由于开环控制下，没有对相位进行约束，不同相位呈现出不同的扰动结果.

(a) 无扬声器扰动

(b) 300 Hz，100%开度扰动

3热声振动时间序列模型

3.1建模方法

(8)

(9)

3.2建模预测结果

3.2.1不同频率扰动下的波形建模

对不同频率扰动下的工况分别建模，由于声压级仅影响波形扭曲的强度，为更好地验证该建模方法的可行性，仅选用扰动最强、声压级为100%开度扰动下的波形进行分析.从采集的压力数据集中随机抽取连续的4 096个数据建立训练集，嵌入维数p设定为10，延迟时间τ设为1，按第3.1节提出的数据处理方法将其转换为矩阵，得到共4 086组数据，输入X为10维向量组，输出Y为由4 086个数据组成的连续时间序列.将建好的模型用于任意一段未参与模型训练的实验采集序列，得到的预测曲线如图3所示，图中给出了100 Hz、200 Hz、300 Hz、400 Hz和500 Hz的压力预测值与实测值的比较，其中误差为二者的差值.从图3可以看出，基于支持向量机的时间序列预测值曲线与实验所测压力曲线基本重合，对于扬声器扰动较小的图3(a)和图3 (b)，其误差也较小，预测值的最大相对误差(误差/实测绝对值的平均值)仅为10.9%；对于扬声器扰动剧烈的情况(图3(c)～图3(e))，预测曲线与实测曲线的吻合度也很高，误差均分布在0附近，只有在数值变化梯度较大的波形峰值区域，预测值可能会出现较大的偏离，在300 Hz的预测曲线中，最大相对误差为43.7%.这是由于支持向量机的全局最优化特性保证了预测模型的泛化能力，但其预测能力还与训练集的信息量和样本数据的分布有关，在数据变化剧烈的区域，模型为保证较好的拟合性能，可能会舍弃某些极端数值.

为了更好地描述该预测模型的拟合情况，定义以下3个参数来描述模型的预测能力：

平均相对误差

(10)

均方根误差

(11)

决定系数

(12)

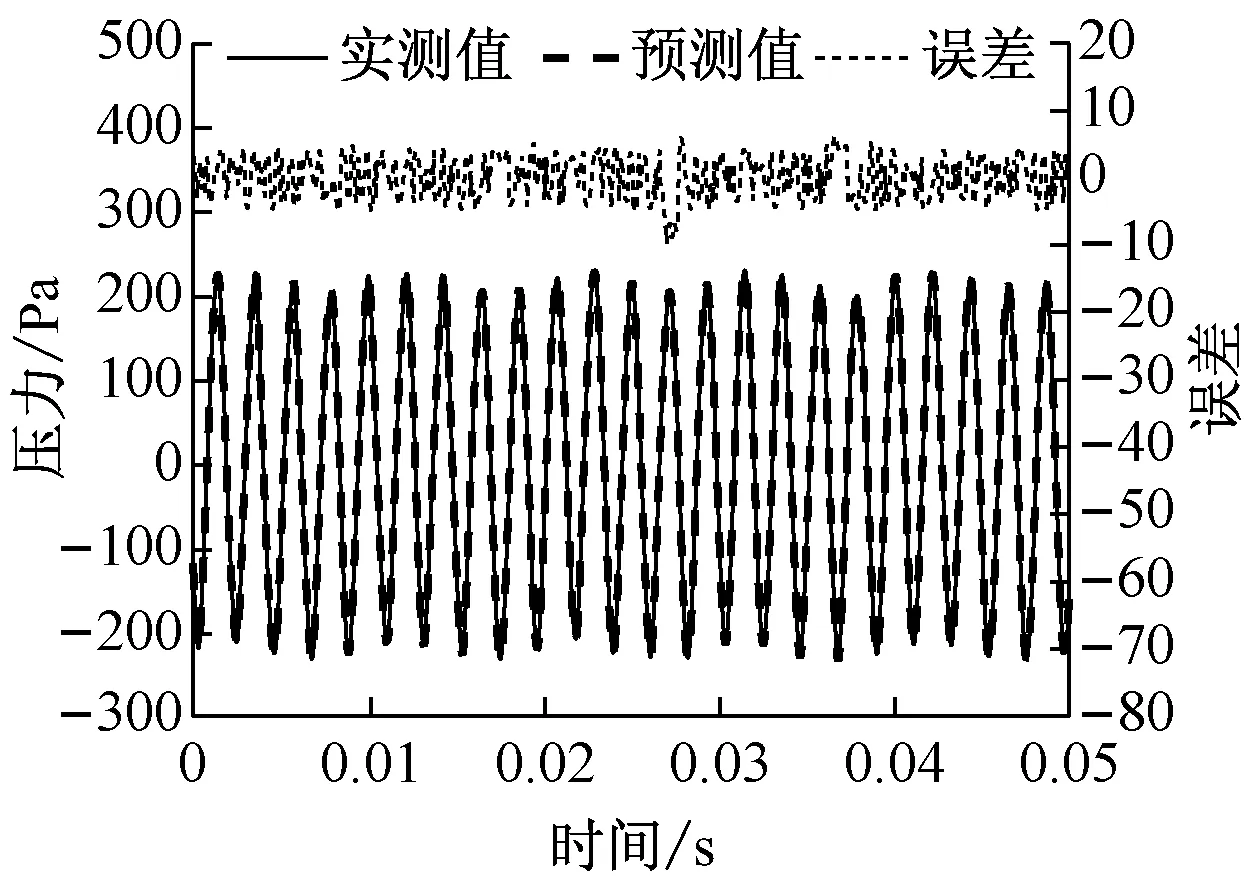
(a) 100 Hz

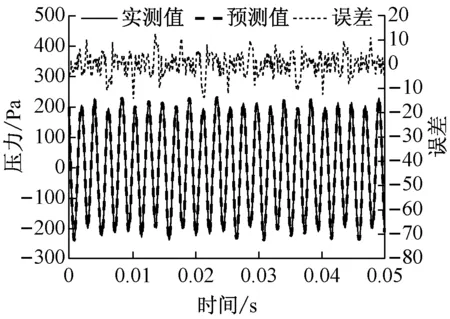
(b) 200 Hz

(c) 300 Hz

(d) 400 Hz

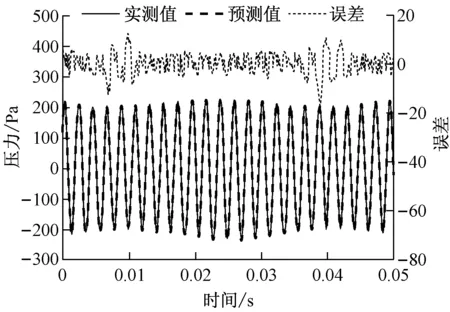
(e) 500 Hz

图4列出了0～500 Hz、100%开度扰动下预测模型的准确度分布，决定系数R2表征了曲线的拟合优度.从图4可以看出，R2分布在[0.998,1]区间，预测值高度贴合实测值，呈现出较好的拟合性能.eMRE和eRMSE描述了预测曲线的平均误差，其中eMRE最高为12%，这是由于实测值在0附近时会产生较大的相对误差，而本文的研究内容并不是很注重这样的相对误差，因此eMRE不能很好地描述该预测曲线的精准性，eRMSE的值更具有参考价值.

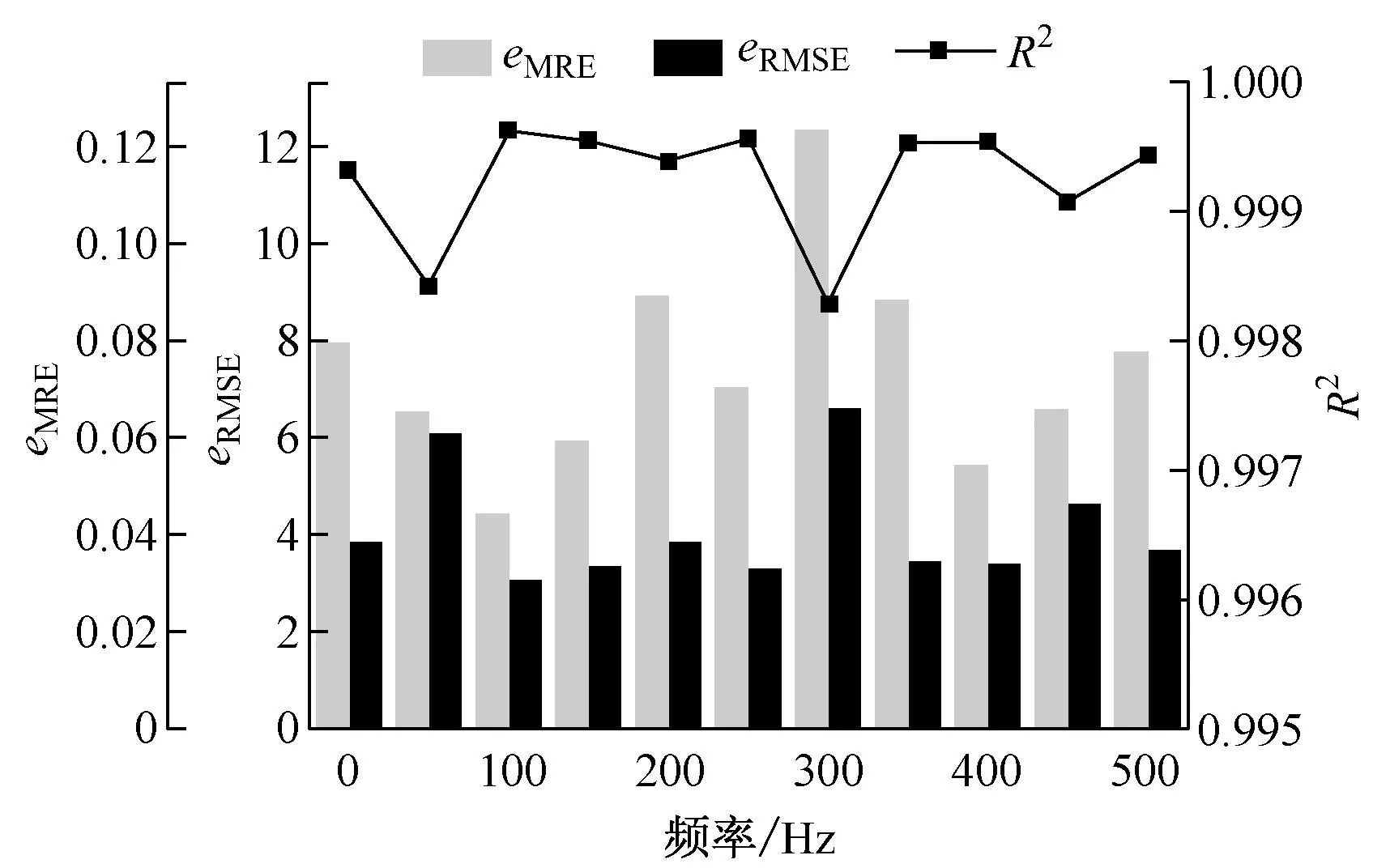
图4　压力波形预测误差分析

3.2.2变工况下的波形建模

当燃烧工况稳定时，采集的是稳定的热声振动数据，但实际燃烧过程在火焰燃烧不稳定或受外界干扰时，容易产生不稳定波形，如图5所示.图5(a)为在火焰燃烧不稳定时采集的压力波形，图5(b)为在极限周期振动下施加不同频率扬声器扰动形成的波形.

(a) 燃烧不稳定波形

(b) 变扰动下的波形

对上述2种波形分别建模预测，预测结果见图6.在变化较复杂的波形中，样本数据非线性相关，训练集和测试集具有不同的关联网络，预测性能会有所下降.图6(a)和图6(b)所示的决定系数R2分别为0.991和0.998，对比第3.2.1节预测结果值偏低，但从图6可以看出，预测值与实测值的重合度仍然较高，满足预测精度的要求.因此该算法具有较强的泛化能力，同样适用于工况不稳定或受外界干扰情况下的热声振动.

(a) 燃烧不稳定波形预测曲线

(b) 变扰动下的波形预测曲线

3.3参数p、τ的影响

在时间序列建模过程中，嵌入维数p和延迟时间τ关系着非线性系统相空间的重构问题，对预测精度有一定的影响.为研究嵌入维数p对预测精度的影响，设定τ=1，p从3取到100，构造训练集、测试集进行时间序列模拟，采用均方根误差eRMSE和决定系数R2评估预测精度(见图7).以往的研究对嵌入维数的取值都较小，为10以下，从图7可以看出，当嵌入维数取到15以下时，模型拥有较高的预测精度，且均方根误差随着嵌入维数的增大而增大.但随着嵌入维数的继续增大，均方根误差不会无限度增大，而是在一定范围内波动，由图7可知，均方根误差维持在[8,13]内来回振荡，决定系数保持在0.99以上，因此，不论嵌入维数取什么值都能满足预测精度要求.综上所述，改变嵌入维数影响着相空间的关联维数，由于时间序列数据呈现一定的周期性变化，嵌入维数影响着关联信息的提取，预测误差会在小范围内反复波动.

图7　嵌入维数对预测误差的影响

笔者对延迟时间的定义与经典Takens[13]理论中的相空间重构不同，相对于Takens数据点相邻间距一致的布置方式，笔者采用的相空间重构法则对热声振动时间序列预测更方便，但会牺牲部分输入-输出数据的关联性.图8为延迟时间τ对时间序列预测精度的影响，其中延迟时间的取值为10～2 000，对应的绝对时间为0.391～78.125 ms，对于本研究课题而言，时间序列预测模型的延迟时间越长越好，预测模型的延迟时间用于抵消控制系统反馈过程中的延迟，文献[7]中提到的简单反馈控制系统阶跃响应测试，其燃烧延迟绝对时间为20 ms.从图8可以看出，预测精度随着延迟时间的增大而降低，在测试的延迟时间范围内，预测误差最高点处τ=1 900，决定系数R2最低为0.95，此时预测曲线仍然具有较高的拟合度，说明对于热声振动时间序列曲线，支持向量机是进行压力波动预测的有力工具.

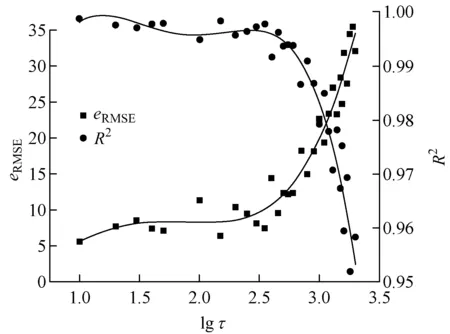
图8　延迟时间对预测误差的影响

4结论

(1) 在自行设计的Rijke管热声不稳定实验台上进行扬声器扰动实验，采集了一系列扰动下的热声振动压力波动曲线，利用支持向量机方法建立了热声振动时间序列的预测模型，对100～500 Hz扬声器扰动下的声场分别进行预测，决定系数分布在[0.998,1]区间，并对不稳定燃烧和变扬声器扰动下的压力波形进行预测，决定系数分别为0.991和0.998，结果表明该建模方法具有较高的拟合度.

(2) 嵌入维数对预测误差的影响不大，预测决定系数随延迟时间的增大而降低，当延迟绝对时间增长到78.125 ms时，决定系数仍能保证在较高的水平，符合预测需求，说明该模型可以用于热声不稳定主动控制系统进行在线预测.

参考文献：

[1]RAYLIEGH J W S. The theory of sound[M].New York:Dover Publications,1945.

[2]BALASUBRAMANIAN K, SUJITH R I. Thermoacoustic instability in a Rijke tube: non-normality and nonlinearity[J].Physics of Fluids,2008,20(4): 044103.

[3]ZHAO D, LEE Y. Experimental investigation of LMS algorithm for active control of combustion instabilities: FIR or IIR[C]// 18th AIAA/CEAS Aeroacoustics Conference. Colorado Springs, USA: AIAA, 2012.

[4]周昊，李时宇，李国能，等．中心射流对旋流燃烧器热声振动的影响[J]．动力工程，2009，29(1)：62-67．

ZHOU Hao, LI Shiyu, LI Guoneng,etal. Effect of central jet on thermoacoustic oscillation of swirl combustor[J].Journal of Power Engineering,2009,29(1): 62-67.

[5]ZHANG Z, GUAN D. Feedback control of Rijke-type thermo-acoustic instability[J].Journal of Low Frequency Noise, Vibration and Active Control,2014,33(4):411-428.

[6]MCMANUS K R, POINSOT T, CANDEL S M. A review of active control of combustion instabilities[J].Progress in Energy and Combustion Science,1993,19(1):1-29.

[7]DOWLING A P, MORGANS A S. Feedback control of combustion oscillations[J]. Annu Rev Fluid Mech,2005,37(1):151-182.

[8]CAMMARATA L, FICHERA A, PAGANO A. Neural prediction of combustion instability[J].Applied Energy,2002,72(2):513-528.

[9]SELIMEFENDIGIL F, ÖZTOP H F. Soft computing methods for thermo-acoustic simulation[J].Numerical Heat Transfer，Part A: Applications,2014,66(3):271-288.

[10]DALEY S, LIU G P. Active control of combustion instabilities[C]// UKACC International Conference on Control'98. Swansea, UK: IET, 1998: 416-421.

[11]CORTES C, VAPNIK V. Support-vector networks[J].Machine Learning,1995,20(3):273-297.

[12]THISSEN U, van BRAKEL R, de WEIJER A P,etal. Using support vector machines for time series prediction[J].Chemometrics and Intelligent Laboratory Systems,2003,69(1/2): 35-49.

[13]TAKENS F.Detecting strange attractors in turbulence[M].Berlin, Germany: Springer Berlin Heidelberg,1981.

SVM Time Series Prediction Model for Active Control of Thermoacoustic Instability

ZHOUHao,DINGFang,HUANGYan

(State Key Laboratory of Clean Energy Utilization, Zhejiang University, Hangzhou 310027, China)

Abstract：To overcome the time delay problem of present thermoacoustic active control system, a method of fuzzily predicting the time series of thermoacoustic instability was proposed using support vector machine (SVM). In the self-developed Rijke tube thermoacoustic instability test bench, the experiments of speaker disturbance were conducted to capture the dynamic pressure sequence under thermoacoustic oscillation, and to build the input and output datasets using phase space reconstruction theory, following which a prediction model was established by SVM and verified with test datasets, and the effects of embedding dimension and time delay on prediction accuracy of the model were qualitatively analyzed. Results show that via the model, high prediction accuracy can be achieved, and the coefficient of determination can get up to 0.95 even if the time delay is large, indicating high degree of fitting, proving the time series prediction method to be effective.

Key words：thermoacoustic instability; Rijke tube; time series; support vector machine; prediction

文章编号：1674-7607(2016)03-0178-07

中图分类号：TK16

文献标志码：A学科分类号：470.1030

作者简介：周昊(1973-)，男，江苏吴江人，教授，博士，主要从事低污染高效燃烧技术方面的研究.电话(Tel．)：13906532015；

基金项目：国家重点基础研究发展计划资助项目(2015CB251501)；国家自然科学基金资助项目(51476137)

收稿日期：2015-04-29

修订日期：2015-06-10

E-mail：zhouhao@cmee.zju.edu.cn.