LSSVM动态软测量模型在磨煤机一次风量预测方面的应用
杨耀权, 张新胜
(华北电力大学 控制与计算机工程学院, 河北保定 071003)
LSSVM动态软测量模型在磨煤机一次风量预测方面的应用
杨耀权,张新胜
(华北电力大学 控制与计算机工程学院, 河北保定 071003)
摘要:针对磨煤机一次风量离线软预测模型难以满足机组变负荷要求的问题,建立了一种自适应修正预测模型参数的LSSVM动态软测量模型.以总的预报误差大小作为阈值来实时更新模型参数,该阈值无需人为参与设定,且能够根据负荷变化自适应改变,并采用网格搜索结合粒子群寻优算法得到LSSVM动态软测量模型中的2个最优参数,应用电厂实际运行数据建立软测量模型并对一次风量动态预测.结果表明:所建立的LSSVM动态软测量模型正确合理、预测精度高(相对误差波动小于1.5%)、实时性好,能很好地实现磨煤机一次风量的实时预测和估计,为磨煤机一次风量的在线监测提供数据支持.
关键词:一次风量; 动态软测量; 最小二乘支持向量机; 预报误差; 运行数据
送风控制系统是火电厂锅炉燃烧控制的3大系统之一,在送风控制系统中,磨煤机一次风量准确可靠的测量是合理的配风、调整磨煤机风煤比、优化燃烧和提高燃烧效率的关键.但是硬件仪表(如差压式流量计、热式质量流量计和机翼式流量计等)的测量受现场安装条件、运行工况变化等方面的限制,容易发生堵塞,使得电厂磨煤机一次风量实时准确地在线监测缺乏数据支持.为解决现场硬件仪表易堵塞、维修不便等问题,应用软测量技术对磨煤机一次风量进行测量的方法得到了很好的发展.
软测量技术[1]的核心思想是利用计算机语言来代替硬件仪表,对实际系统中不可测量或测量精度低的主导变量,以易测的过程变量(辅助变量)建立软测量模型进行预测.其中最小二乘支持向量机[2-3](LSSVM)在软测量技术中得到了很好的应用,然而由于火电机组运行时变负荷已经成为常态,在磨煤机一次风量预测应用中所建立的LSSVM预测模型无法满足变负荷的要求,造成其预测精度低、泛化能力弱,仅能满足稳态工况下的精度要求.为此,笔者建立了基于LSSVM的磨煤机一次风量动态软测量模型.
笔者以某600 MW机组磨煤机一次风系统为研究对象,根据电厂实际运行数据,通过简单的机理和相关性分析,确定一次风量在预测模型中的辅助变量,并建立基于运行数据自适应修正预测模型参数的LSSVM一次风量动态软测量模型,以总的预报误差的大小作为阈值判断是否更新模型参数,阈值的设定可以根据负荷变化自适应地变化,使得预测模型在机组变负荷运行时满足预测精度和实时性的要求.
1LSSVM数学模型和算法原理
最小二乘支持向量机[3-4]是传统SVM的一种特殊扩展,按照统计理论的VC维理论和结构风险最小化(Structural Risk Minimization,SRM)准则,LSSVM的方法相当于求解如下最小非线性规划问题[5-6]:
(1)
式中:w为权向量;b为偏置量;c为惩罚因子;ei为误差;Φ(·)为线性映射函数;i=1,2,…,m.
定义核函数K(xi,xj)代替线性映射函数,引入Lagrange函数,并利用KKT条件将式(1)变成求解如下方程组:
(2)
在求解Lagrange因子λ与偏置量b时,假设:
(3)
(4)

(5)
其中A-1可利用分块矩阵求逆得到,通过式(5)求得LSSVM模型参数的解:
(6)
通过式(6)可知,计算Lagrange因子λ和偏置量b的关键在于求解矩阵K的逆矩阵,通过观察矩阵K的特点,可以利用迭代算法求得矩阵K的逆矩阵,即
(7)
其中,β=[K(x1,xn+1)K(x2,xn+1)…K(xn,xn+1)]T,θ=K(xn+1,xn+1)+1/c.
由分块矩阵求逆可得:
(8)

通过式(8)可知,求解矩阵K-1的过程为:得到新的样本数据后,首先计算求得矩阵β和常数θ;再由上次计算求得的K-1计算得到矩阵B、C和常数η,然后代入式(8)计算得到本次K-1.由此可知,采用迭代算法计算K-1大大简化了计算复杂度,提高了LSSVM模型的更新速度.将K-1代入式(6)可以求得Lagrange因子λ和偏置量b,从而得到LSSVM模型的输出方程为
(9)
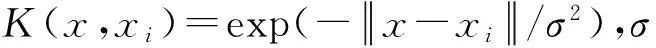
2基于LSSVM的动态软测量模型
以某600 MW机组磨煤机一次风系统为研究对象,建立磨煤机一次风量的LSSVM动态软测量模型[6],主要包括LSSVM离线软测量模型的建立和动态软测量模型的实现2个部分.
2.1基于LSSVM的离线软测量模型
磨煤机一次风量的LSSVM离线软测量模型不考虑一次风量的动态变化,利用辅助变量估算出一次风量的大小.其中辅助变量的选取与训练样本数据预处理是整个方案实现的前提,LSSVM模型的建立是整个方案的核心和关键.
2.1.1辅助变量的选择
从电厂获得的DCS数据包括了一次风从一次风机入口到磨煤机出口的整个过程中各个设备运行参数的测点数据,磨煤机一次风系统的工艺流程如图1所示.结合流量测量的基本原理和影响一次风量测量的因素,选取磨煤机一次风系统运行过程中主要影响一次风量的11个相关变量作为辅助变量,即:一次风机A电流IA、一次风机A动叶开度OA、空气预热器A出口与一次风机A出口温差TA、一次风机B电流IB、一次风机B动叶开度OB、空气预热器B出口与一次风机B出口温差TB、磨煤机电流IC、磨煤机瞬时给煤量M、磨煤机一次风与磨煤机分离器压差p、磨煤机冷风调门开度OC、磨煤机热风调门开度OH.
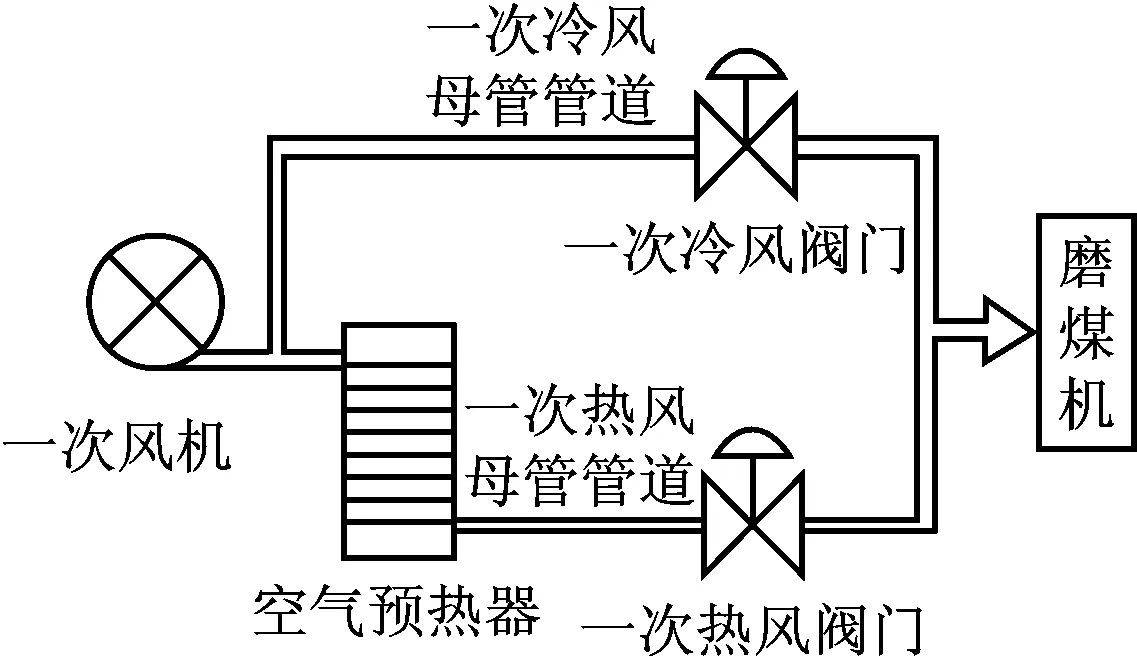
图1 磨煤机一次风系统工艺流程图
2.1.2数据预处理
数据预处理主要包括数据误差处理和数据归一化处理,由于本文训练样本数据在某电厂DCS的SAMA图中已经过了滤波处理,所以不再对数据进行误差处理.在选取训练样本数据时,训练样本集的规模特别大、有的数据之间的相似度特别高,不满足LSSVM小样本数据的特征,所以需要对样本数据进行优化处理,利用相似度函数的方法优化训练样本数据.
相似度函数优化数据的核心思想[7-8]是:利用相似度函数计算出2组数据之间的相似程度,对于相似度高的数据,只保留其中一组数据,删除另一组数据,进而减少训练样本数据之间的冗余.笔者选取的相似度函数为
(10)
式中:xi表示第i组样本数据;xj表示第j组样本数据;Rij表示2组数据之间的相似程度;δ为归一化参数.
数据的优化原则为:若Rij<ε,则保留这2组数据;若Rij≥ε,则保留1组数据.
如果直接将工程单位不同的辅助变量利用相似度函数优化后的数据作为LSSVM模型的输入,会造成模型的不稳定,因此需要对训练样本数据进行归一化处理,将所有的数据都转换为[-1,1]之间的数,进行数据归一化的变换式为
(11)
2.1.3LSSVM离线软测量模型的建立
将样本数据优化后的11个辅助变量经过归一化处理后作为LSSVM模型的输入变量,磨煤机一次风量的大小作为输出变量.为了得到较好的性能,在LSSVM建模时选取径向基函数作为核函数,采用网格搜索结合粒子群(PSO)算法确定模型中参数sig2和gam的最优值.图2给出了LSSVM离线软测量模型的拓扑结构.
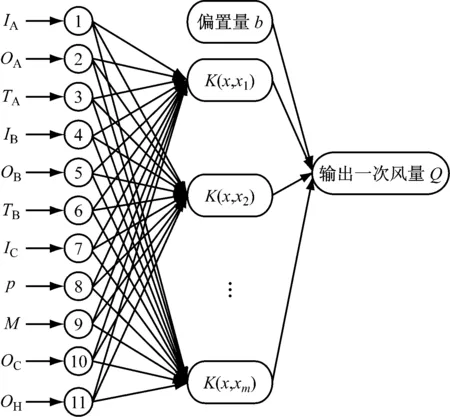
图2 LSSVM离线软测量模型的拓扑结构
由图2可知,基于LSSVM的磨煤机一次风量离线软测量模型为
Q=f(IA,OA,TA,IB,OB,TB,IC,M,p,OC,OH)
其中,Q表示磨煤机一次风量.
2.2LSSVM动态软测量模型的实现
在火电厂的变负荷运行常态下,所建立的LSSVM离线软测量模型只能满足与训练样本处于相同或相近工况的预测精度要求,而在其他工况下预测精度较低,无法满足现场需求.因此需要建立LSSVM动态软测量模型,即考虑一次风量的动态变化,自适应地修正模型参数,不断丢弃旧的训练样本,同时加入新的数据作为训练样本,所建立的LSSVM模型不仅能满足当前工况的预测精度要求,还可以确保模型的实时性.笔者提出了利用总的预报误差作为阈值,当有新的样本进入模型时,以此阈值判断是否更新模型参数,该阈值还可以根据运行工况的变化自适应改变,无需人为设定.
2.2.1LSSVM预报误差
基于LSSVM的磨煤机一次风量的预报误差定义为在某组样本数据下磨煤机一次风量的实际值与去掉这组样本数据后LSSVM模型预测出的一次风量的差值.LSSVM预报误差的大小可以根据矩阵计算推导得出,假设去掉训练样本数据中的第一组数据,预报误差[9]的推导如下:
将式(2)改写为
(12)
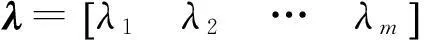
(13)
(14)
所以去掉训练样本中第一组数据后的LSSVM模型对第一组样本数据的磨煤机一次风量的预测值为
(15)
将式(13)、式(14)代入式(15)化简可得:
(16)
第一组样本数据对应的磨煤机一次风量的实际值可以表示为
(17)
所以基于LSSVM的磨煤机一次风量的预报误差为
(18)
利用分块矩阵对矩阵A求逆可知A-1(1,1)=A11-aMaT,所以简化式(18)可得LSSVM预报误差为
(19)
在求解线性方程组时,由于交换方程组中方程的次序不改变方程的解,所以当任意去掉某组训练样本数据时LSSVM的预报误差为
(20)
式中:A-1可由K-1利用分块矩阵求逆算得,由式(8)可知,K-1可由迭代算法求得,即A-1也可以利用迭代算法求得,无需重复计算.
因此,总的LSSVM预报误差为
(21)
2.2.2LSSVM动态软测量模型的建立
建立一个随时间滑动的模型数据窗口,该窗口的大小定义为离线软测量模型LSSVM建模时训练样本数据的个数.根据式(21)计算得到总的预报误差,进而判断是否更新模型参数,如果需要更新时,选择删除预报误差中最小的训练样本,将新的样本放入训练样本模型中,重新计算Lagrange因子λ和偏置量b,得到新的LSSVM模型.具体步骤如下:
(1) 建立LSSVM离线软测量模型,计算得到Lagrange因子λ和偏置量b,定义滑动窗口大小为训练样本数据的个数.
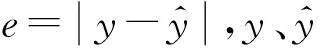
(3) 根据式(21)计算得到总的预报误差,若Ep/m≤e,则更新LSSVM模型参数;否则放弃更新,继续等待新的样本数据.
根据步骤(3)可知,当Ep/m≤e时,需要更新LSSVM模型参数,即需要重新计算Lagrange因子λ和偏置量b,根据式(6),计算矩阵K的逆矩阵是得出模型参数的关键,而矩阵K的逆矩阵可利用迭代算法求得,由于滑动窗口中的训练样本数据删去了一组预报误差最小的数据,所以矩阵K发生了改变,对应的逆矩阵也发生了改变,矩阵大小上比原来少了一行一列,根据矩阵计算,推导出变化前后矩阵K的逆矩阵之间的关系如下:
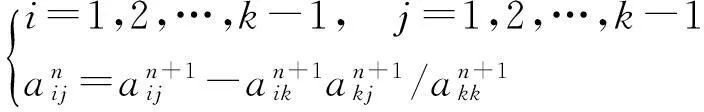
(22)
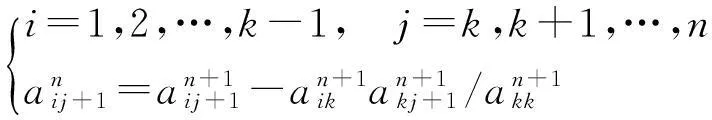
(23)
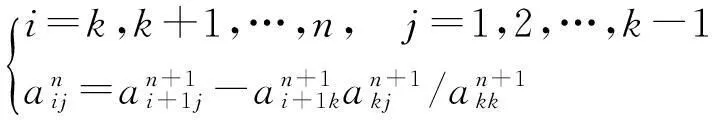
(24)
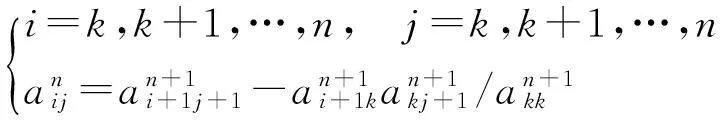
(25)
3动态软测量模型的训练及仿真效果
3.1样本数据介绍
笔者选择某电厂一天的磨煤机一次风系统运行数据,等时间间隔下采集1 000组样本数据,利用相似度函数优化所选的样本数据,将优化后的数据作为离线LSSVM模型的输入数据.在进行数据样本优化时剩余样本数随相似度函数阈值的不同而不同,如图3所示.
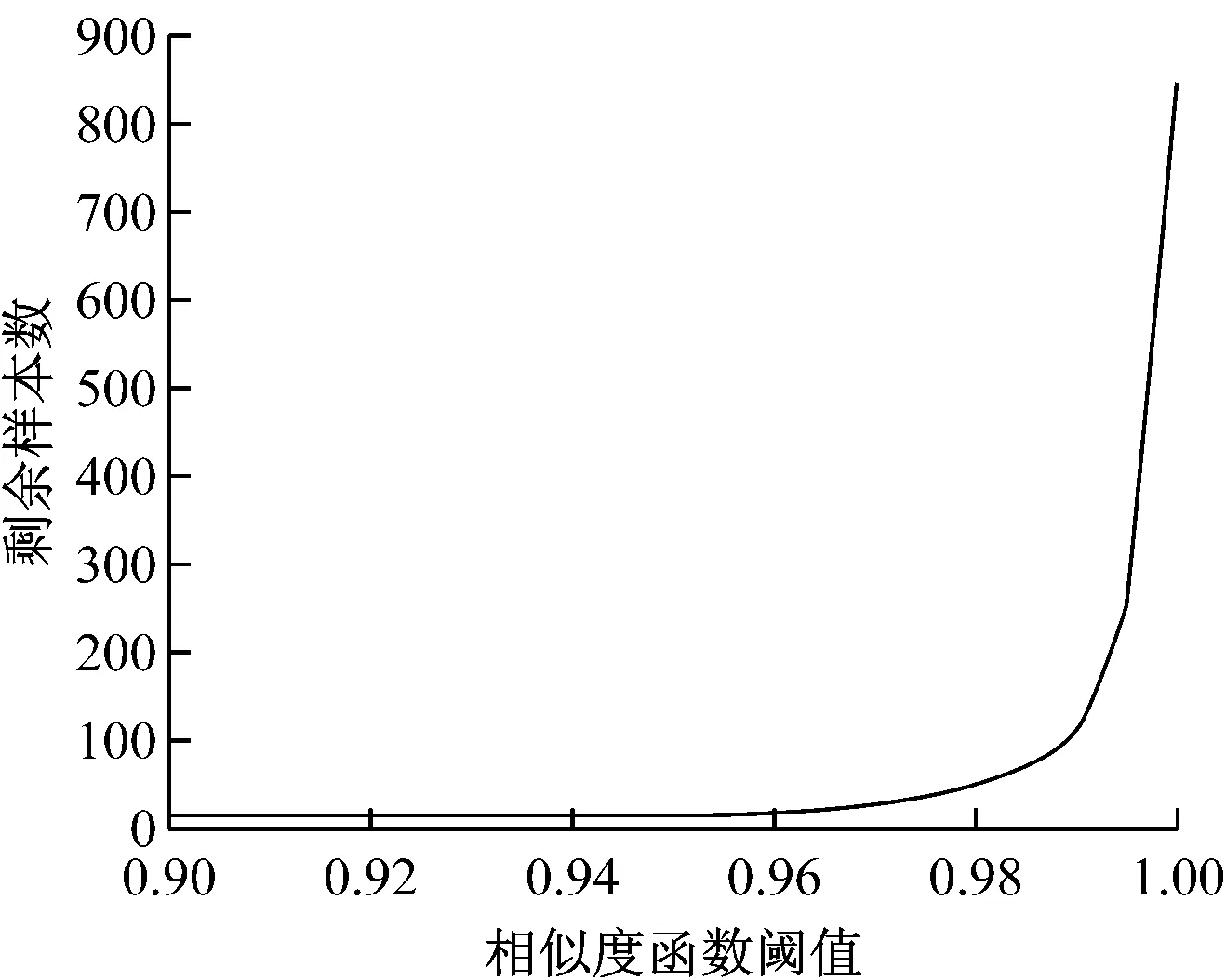
图3 剩余样本数随相似度函数阈值的变化
由图3可知,随着相似度函数阈值的增加,剩余样本数据的个数逐渐增加,当相似度函数阈值处于[0.98,1.00]时曲线的变化最大,说明此时优化数据样本效率最高,即在此区间数据之间存在的冗余信息最多,因此选择阈值大小为0.99,优化后样本数据剩余107组.此外在另一个运行工况下选取1 000组测试样本数据,优化后测试样本数据为125组.
3.2预测结果与分析
利用上文样本优化后选出的125组运行数据对基于LSSVM的磨煤机一次风量动态软测量模型的精度与可行性进行检验.LSSVM核函数选择径向基核函数,LSSVM的正规化参数sig2和核函数参数gam的最优范围由网格搜索得到,再利用PSO算法[10]在线寻优获得其最优值,其中最优参数sig2=12.141 8,gam=240.580 5.将建立好的LSSVM动态软测量模型(简称LSSVM动态模型)应用于磨煤机一次风质量流量的预测中.同时,在此基础上还利用LSSVM离线软测量模型(简称LSSVM离线模型)对同一测试样本进行了预测.图4和图5分别给出了LSSVM动态模型预测值、LSSVM离线模型预测值与实际磨煤机一次风质量流量的比较.由图4和图5可知,基于LSSVM动态模型的磨煤机一次风质量流量预测值更接近其实际值.为了精确说明LSSVM动态模型预测实时性好的特点,对磨煤机一次风质量流量每个预测时刻点的在线仿真时间进行了计算,在线仿真时间都小于0.5 s.
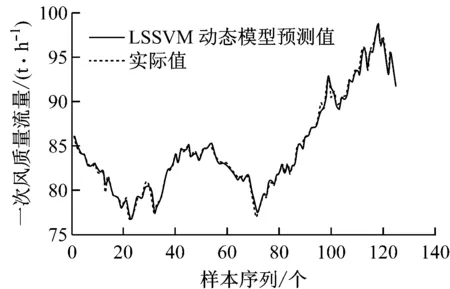
图4 LSSVM动态模型预测值与实际值的比较

图5 LSSVM离线模型预测值与实际值的比较
3.3预测误差分析
为了比较LSSVM动态模型与LSSVM离线模型的预测精度,对2个模型的相对误差进行分析,结果如图6所示.由图6可知,相比LSSVM离线模型,LSSVM动态模型预测的磨煤机一次风质量流量相对误差曲线起伏小,波动范围在1.5%以内,最大相对误差为1.2%,而LSSVM离线模型预测的最大相对误差为8.7%,因此在预测精度上LSSVM动态模型明显优于LSSVM离线模型.
将最大绝对值误差Emax与均方根误差ERMSE作为模型评价的性能指标,计算结果如表1所示.由表1可知, LSSVM动态模型预测的磨煤机一次风质量流量在预测性能方面要优于LSSVM离线模型.
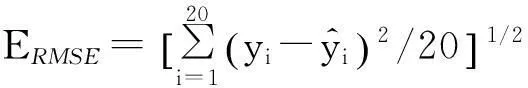
(26)
(27)
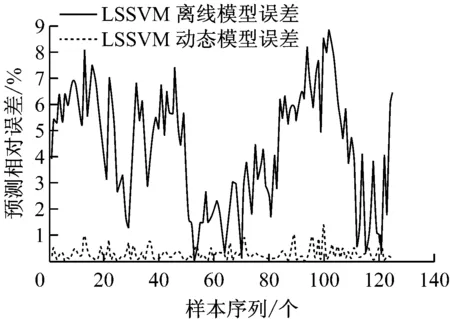
图6 LSSVM动态模型与LSSVM离线模型相对误差的对比

模型Emax/(t·h-1)ERMSE/(t·h-1)LSSVM动态模型1.25710.3345LSSVM离线模型7.93544.1422
4结论
(1) 利用递进迭代的算法计算出LSSVM模型的Lagrange因子λ和偏置量b,降低了模型计算的复杂度,大大提高了模型的更新速度.
(2) 在LSSVM离线软测量模型的基础上建立了LSSVM动态软测量模型,该动态软测量模型以滑动窗口中总的预报误差作为阈值,且该阈值可以根据运行工况自适应改变,从而提高了模型的全局推广性能.
(3) 在磨煤机一次风量的预测应用中,所建立的LSSVM动态软测量模型的最大相对误差为1.2%,每个预测时刻点的在线仿真时间小于0.5 s,表明所建立的动态软测量模型正确合理,预测精度高,实时性好,为电厂磨煤机一次风量的准确、实时在线监测提供了数据支持.
参考文献:
[1]陈彦桥,郭一,刘建民,等.一种改进烟气含氧量软测量建模方法与仿真[J].动力工程学报,2011,31(1):12-16.
CHEN Yanqiao,GUO Yi,LIU Jianmin,etal.An improved modeling method for soft-sensing of oxygen content in flue gas and the simulation[J].Journal of Chinese Society of Power Engineering,2011,31(1):12-16.
[2]刘吉臻,吕游,杨婷婷.基于变量选择的锅炉NOx排放的最小二乘支持向量机建模[J].中国电机工程学报,2012,32(20):102-107.
LIU Jizhen,LÜ You,YANG Tingting.Least squares support vector machine modeling on NOxemission of boilers based on variable selection[J].Proceedings of the CSEE,2012,32(20):102-107.
[3]顾燕萍,赵文杰,吴占松.基于最小二乘支持向量机的电站锅炉燃烧优化[J].中国电机工程学报,2010,30(17):91-97.
GU Yanping,ZHAO Wenjie,WU Zhansong. Combustion optimization for utility boiler based on least square-support vector machine[J].Proceedings of the CSEE,2010,30(17):91-97.
[4]MUSTAFFA Z,YUSOF Y,KAMARUDDIN S S.Application of LSSVM by ABC in energy commodity price forecasting[C]//Power Engineering and Optimization Conference.Lankawi, Malaysia:IEEE, 2014:94-98.
[5]洪文鹏,刘广林.基于最小二乘支持向量机的氨法烟气脱硫装置脱硫效率预测[J].动力工程学报,2011,31(11):846-850.
HONG Wenpeng,LIU Guanglin.Efficiency prediction for an ammonia flue gas desulphurization system based on least squares-support vector machine[J].Journal of Chinese Society of Power Engineering,2011,31(11):846-850.
[6]王磊,李桂香,王元麒,等. 基于LSSVM的天然气脱CO2膜分离在线软测量模型[J].系统仿真学报,2014,26(8):1836-1840.
WANG Lei,LI Guixiang,WANG Yuanqi,etal.On-line soft measurement model for CO2separating from natural gas membrane separation process based on LSSVM[J]. Journal of System Simulation,2014,26(8):1836-1840.
[7]张传标,倪建军,苗红霞,等.基于相似度的核主元分析方法及其应用研究[J].计算机工程,2011,37(14):239-241.
ZHANG Chuanbiao,NI Jianjun,MIAO Hongxia,etal.Study on kernel principal component analysis method based on similarity and its application[J].Computer Engineering,2011,37(14):239-241.
[8]金秀章,韩超. KPCA-LSSVM在磨煤机一次风量预测中的应用[J].自动化仪表,2015,36(3):62-67.
JIN Xiuzhang,HAN Chao.Application of KPCA-LSSVM in prediction of the primary air flow of pulverizer[J].Process Automation Instrumentation,2015,36(3):62-67.
[9]张英堂,马超,李志宁,等.基于快速留一交叉验证的核极限学习机在线建模[J].上海交通大学学报,2014,48(5):641-646.
ZHANG Yingtang,MA Chao,LI Zhining,etal.Online modeling of kernel extreme learning machine based on fast leave-one-out cross-validation[J].Journal of Shanghai Jiaotong University, 2014,48(5):641-646.
[10]洪文鹏,陈重.基于自适应粒子群优化BP神经网络的氨法烟气脱硫效率预测[J].动力工程学报,2013,33(4):290-295.
HONG Wenpeng,CHEN Zhong.Efficiency prediction of ammonia flue gas desulfurization based on adaptive PSO-BP model[J].Journal of Chinese Society of Power Engineering,2013,33(4):290-295.
Soft-sensing of Primary Air Flow in a Coal Mill Based on LSSVM
YANGYaoquan,ZHANGXinsheng
(School of Control and Computer Engineering, North China Electric Power University,Baoding 071003, Hebei Province, China)
Abstract:To solve the problem that the off-line soft-sensing model for primary air flow in coal mill of a power unit can not satisfy the requirement of variable load operation, a dynamic soft-sensing model based on LSSVM was proposed, which is able to adaptively modify the model parameters by taking the total prediction error as a threshold to update the model parameters in real time without any manual work according to the load variation. Two optimal parameters of LSSVM model were obtained by grid search and PSO algorithm. The model was trained with actual operation data of a power plant, and was then used to dynamically predict the primary air flow. Results show that the LSSVM soft-sensing model is reasonable and accurate (maximal error less than 1.5%), with good real-time performance, which is able to realize real-time prediction of the primary air flow, and therefore may serve as a reference for on-line monitoring of the primary air flow in coal mills.
Key words:primary air flow; dynamic soft-sensing; LSSVM; prediction error; operating data
文章编号:1674-7607(2016)03-0207-06
中图分类号:TK313
文献标志码:A学科分类号:470.20
作者简介:杨耀权(1962-),男,河北保定人,教授,硕士生导师,研究方向为智能测控技术、数字图像处理.
收稿日期:2015-05-27
修订日期:2015-07-15
张新胜(通信作者),男,硕士研究生,电话(Tel.):13582234091;E-mail:1271904927@qq.com.

