基于滚动时间窗的PSO—LSSVM的通信基站能耗建模
张英杰+许伟+汤龙波+张营+刘文博+胡作磊+范朝冬

摘 要:基站是通信网络的重要能耗节点,精准计算合同能源管理(EPC)模式下基站节能量成为该领域的技术瓶颈.以3类典型场景通信基站为对象,提出了一种基于粒子群优化算法(PSO)的滚动时间窗最小二乘支持向量机(LSSVM)的基站能耗建模方法.该方法通过选取预处理的基站配置参数与实时数据建立滚动时间窗,采用PSO优化训练模型参数,并通过LSSVM回归估计训练模型,得到随时间窗数据变化的基站动态能耗模型.仿真试验与样本基站实测数据的验证结果表明,本文建立的能耗模型具有较高的预测精度及泛化能力,对基站节能工程的评估具有良好的应用前景.
关键词:通信基站;能耗模型;最小二乘支持向量机;粒子群;滚动时间窗
中图分类号:TP18;TN929.5 文献标志码:A
Modelling of Base Station Energy Consumption System
Based on Sliding Window PSO-LSSVM
ZHANG Yingjie1,2,XU Wei1,2,TANG Longbo1,2, ZHANG Ying1,2,
LIU Wenbo1,2,HU Zuolei1,2,FAN Chaodong3
(1. College of Information Science and Engineering,Hunan University, Changsha 410082, China;
2.Institute for Communications Energy Conservation, Hunan University, Changsha 410082, China;
3.The College of Information Engineering, Xiangtan University, Xiangtan 411105, China)
Abstract:Base station is a major node for communication network's energy consumption. The accurate calculation of the energy-saving amount for the base station under EPC model is a technology bottleneck in this field. This paper proposed a modeling method of energy consumption of the base station based on particle swarm optimization (PSO) and least squares support vector machine (LSSVM) of sliding window, oriented at three kinds of typical scenarios base station. In this approach, a sliding window was established by selecting configuration parameters of base station and real-time data for pretreatment, and then the dynamic energy consumption model was obtained for the base station, which varied in accordance with that of the sliding window by means of the parameters for PSO training model and LSSVM regression training model. Compared with the simulation and test results from the sample base station, the proposed energy consumption model shows high prediction accuracy and generalization ability, and is applicable for the evaluation of energy-saving engineering of the base station.
Key words:base station;energy consumption model;LSSVM(Least Squares Support Vector Machine);PSO(Particle Swarm Optimization);sliding window
隨着通信业务快速发展,通信业能源消耗也呈快速增长趋势,而通信基站是通信行业能耗的重点,因此,持续有效地整体推进通信基站节能降耗已经成为通信行业节能减排的关键.从目前的形势来看,通信基站的合理设计及节能措施的选择还未形成一个完整体系[1],通信节能发展的瓶颈是过于概念化和粗放型的能源规划,不断增加节能设备,缺少综合信息集成应用、运行监管及评估体系.所以,研究并建立能够精确计算基站能耗的数学模型,对通信企业节能减排和基站用电的精细化管理具有积极的意义.通信基站能耗系统主要由电源系统(包括通信电源、蓄电池组),基站主设备(包括BTS、天馈系统、BSC),环境设备(包括基站空调、新风系统、热交换系统)以及辅助系统(包括照明设备、监控系统)等部分构成.基站总能耗主要集中在通信设备用电和机房环境用电,通过实际调研及实测数据计算可知,通信基站能耗主要由主设备能耗和空调系统能耗构成.主设备能耗主要包括无线设备能耗、电源损耗与传输设备能耗等,其中无线设备能耗为主要能耗点[2],而空调系统耗能与设备发热量以及整个基站的热传导情况直接相关;同时,空调系统能耗还受到气象条件、建筑环境及内部运行设备等多方面因素的影响.由于通信基站能耗的相关特征数据(包括基站建筑材料及结构属性、基站所处位置及外部环境特征、基站设备参数、气象参数等)复杂多变,同时要考虑环境条件的约束,所以通信基站能耗建模具有一定的复杂性[3].
在通信行业,能耗建模相关研究主要集中在基站主设备能耗计量、空调能耗计量及空调节能量计算、基站能耗分类建模等方面.周小兵[4]以广东中山地区90 mm厚彩钢板结构通信基站为研究对象,利用基站总耗电量、空调及新风系统耗电量、室内外气温的实测数据计算空调基准耗电量的方法,方便准确地得到了空调基准耗电量,对核定通信基站节电量具有一定的参考价值.杨苹等人[5]根据基站内外部特征,分析了外部环境因素和内部设备构成对基站能耗的影响,建立了基于建筑能耗分析软件DeST的基站能耗模型;通过DeST进行通信基站能耗分析具有一定的局限性,且模型准确率低,不能作为理想的能耗预测模型.杨天剑等人[6]通过多元线性回归确立影响基站耗电量的主要因素,然后通过聚类算法将大量基站能耗数据分类,最后通过能耗标杆得到了通信基站的耗能预测模型;该方法通过多元线性回归和聚类分析得到基站能耗标杆,在设备环境参数和能耗关系上具有一定研究意义,但对基站整体能耗预测尚有不足.李阳[7]以基站的热平衡模型为基础,应用Simulink仿真软件对基站能耗进行动态仿真建模,同时,对基站当前使用的主要节能技术进行建模,构建出一个较完整的基站能耗动态仿真模型;该研究模型主要应用于仿真模拟,实际应用到通信基站能耗计量方面仍有缺陷.虽然众多研究机构及学者在通信基站能耗建模方面做了大量的工作,但建立起来的概念型与统计型的能耗模型也只能在基站能耗预测预警与节能措施选择时起到一定的辅助决策作用,仍然缺乏一个能够实时精确计算基站能耗的模型.
基于此,本文综合考虑了通信基站总耗电量、主设备耗电量、空调耗电量、电源系统耗电量、外部气象参数、室内外温度、基站环境特征、建筑材料及结构等数据,通过对不同类型典型场景基站进行动静态数据采集,分析基站能耗与时间、空间、环境参数等数据间的多维关系,找出基站能耗的主要影响因素,并采用基于滚动时间窗的PSO-LSSVM算法建立准确计量基站能耗的多输入复杂系统能耗模型.
1 基于滚动时间窗的最小二乘支持向量机
1.1 支持向量机理论
支持向量机(Support Vector Machine,SVM)是Vapnik于20世纪90年代初依据统计学理论提出的一种基于数据的机器学习算法.支持向量机的基本原理是通过非线性映射把输入向量映射到一个高位特征空间,在该空间用线性学习机方法以解决原空间的非线性分类和回归等问题.SVM最初是用来解决模式识别中的分类问题,后来Vapnik通过定义ε不敏感损失函数提出了支持向量机回归算法(SVMR),用于解决非线性回归问题[8].
支持向量机能够将算法转化为线性规划或二次规划问题,从而解决局部极小问题,实现全局最优;用核函数代替高维特征空间的内积运算,使得高维空间问题得到很好的解决.同时,它可以通过容量调节惩罚参数来平衡拟合能力和泛化能力间的权重关系,具有结构简单、稀疏性好等优点[9].支持向量机能够较好地实现结构风险最小化准则,也能很好地处理非线性、高维数、局部极小以及过学习等实际问题.在建筑、水利、气象、医学等领域支持向量机已经成功应用到分类、预测及预警中.
1.2 LSSVM算法介绍
支持向量机在计算时每增加一个样本数据就需要求解一个二次规划问题,不仅增加了运算量而且实时性较差.为了解决这种问题,Suykens等人[10]提出了最小支持向量机(Least Squares Support Vector Machines,LSSVM)理论.
给定训练样本集D={xi,yi}Ni=1,其中N为训练样本量,xi∈Rm为m维输入,yi∈R为一维目标输出.将样本空间中的非线性函数估计问题转化为高维特征空間中的线性函数估计问题[11-12].
f(x)=wTφ(x)+b (1)
式中:w=[w1,…,wn]T为权值系数向量;φ(·)=[φ1(·),…,φn(·)]T为映射函数.这一回归问题可以表示为一个等式约束优化问题,其优化目标为:
minw,b,eJ(w,e)=12wTw+λ2∑ni=1e2i(2)
s.t. yi=wTφ(xi)+b+ei,i=1,…,n(3)
然后,用拉格朗日法求解上述优化问题:
L(w,b,e,a)=J(w,e)-∑Niai(wTφ(xi)+
b+ei-yi)(4)
式中:ai(i=1,…,n)为拉格朗日乘子.
根据优化条件对式(4)求偏导可得:
Lw=0→w=∑Ni=1aiφ(xi)
Lb=0→∑Ni=1ai=0
Lei=0→ai=γei
Lw=0→wTφ(xi)+b+ei-yi=0(5)
再根据Mercer条件,定义核函数:
k(xi,yi)=φT(xi)φ(yi).(6)
由方程式(5)和(6)消去ei,w后,得到
0 1 … 1
1 k(x1,x1)+1/γ … k(x1,xn)
1 k(xn,x1) … k(xn,xn)+1/γ×
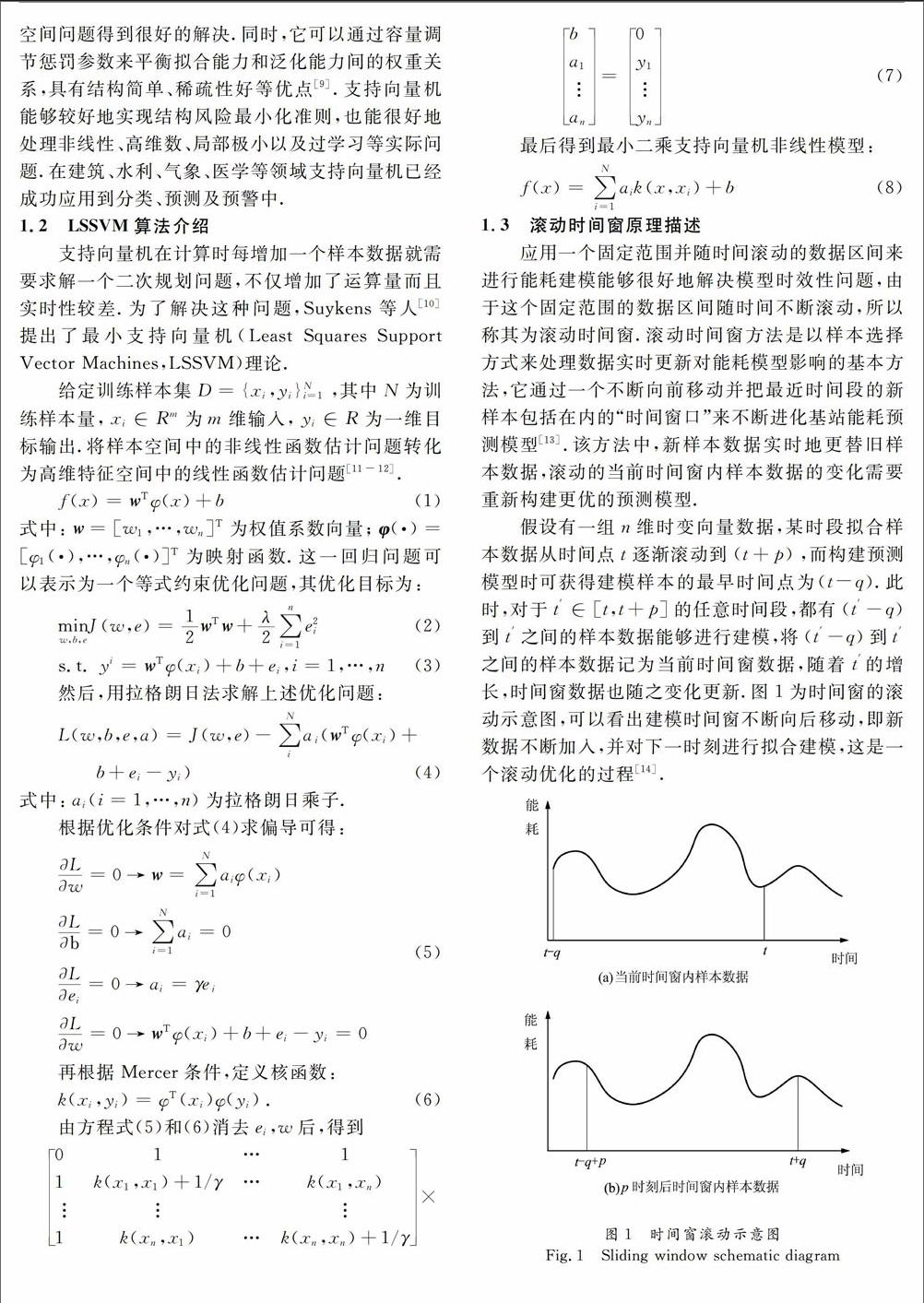
ba1 an=0y1 yn(7)
最后得到最小二乘支持向量机非线性模型:
f(x)=∑Ni=1aik(x,xi)+b(8)
1.3 滚动时间窗原理描述
应用一个固定范围并随时间滚动的数据区间来进行能耗建模能够很好地解决模型时效性问题,由于这个固定范围的数据区间随时间不断滚动,所以称其为滚动时间窗.滚动时间窗方法是以样本选择方式来处理数据实时更新对能耗模型影响的基本方法,它通过一个不断向前移动并把最近时间段的新样本包括在内的“时间窗口”来不断进化基站能耗预测模型[13].该方法中,新样本数据实时地更替旧样本数据,滚动的当前时间窗内样本数据的变化需要重新构建更优的预测模型.
假设有一组n维时变向量数据,某时段拟合样本数据从时间点t逐渐滚动到(t+p),而构建预测模型时可获得建模样本的最早时间点为(t-q).此时,对于t′∈[t,t+p]的任意时间段,都有(t′-q)到t′之间的样本数据能够进行建模,将(t′-q)到t′之间的样本数据记为当前时间窗数据,随着t′的增长,时间窗数据也随之变化更新.图1为时间窗的滚动示意图,可以看出建模时间窗不断向后移动,即新数据不断加入,并对下一时刻进行拟合建模,这是一个滚动优化的过程[14].
2 PSO优化的LSSVM算法
支持向量机在精度和效率上的优越性跟其参数的取值密切相关,但是其参数数量很多而且参数的选择范围很大,这样就使得最优参数的选取变得困难.同时,由于最小二乘支持向量机模型是非线性的,采用解析的方法得到其模型参数几乎不可能,使用数值计算也很难得到真正的最优参数,所以,必须选择一个合适的模型参数优化方法.
2.1 基于PSO算法优化模型参数
LSSVM模型中径向基核函数的选用需要确定两个参数:核参数σ和惩罚因子γ.γ越小,模型泛化能力越强,平滑性越好,但是拟合能力会降低;而σ越大,所得训练模型就会越平滑,泛化能力也越强;同时,粒子也是由这两个参数所决定,所以他们的优化必不可少.通常我们采用参数空间穷尽搜索法对LSSVM参数进行优化,但其缺点是较难确定合理的参数范围.而本文采用PSO优化LSSVM参数能够很好地解决这种问题,且能够快速准确地选取到最优参数.
粒子群算法PSO(Particle swarm optimization,PSO)是1995年由Kennedy和Eberhart[15]提出的一种启发式搜索算法.最初,PSO算法从鸟群觅食行为中得到启发,然后图形化模拟鸟群的不可预测运动,并以此作为算法的基础.然后引入近邻的速度匹配、惯性权重w,并考虑多维搜索和距离的加速,形成了最初的PSO算法[16].
与其他进化算法类似,粒子群算法采用“种群”的方式不断“进化”自己的搜索模式.在PSO算法中,可以将优化问题的每个潜在解看成是多维空间中的一个“点”,将各异的“点”称做“粒子”,多个“粒子”就组成一个群体.当PSO初始化生成一群随机粒子(即随机解)后,粒子即开始不断迭代来找到最优解,在这个过程中,每个粒子都有自己运动的方向及速率,即粒子都有一个矢量速度,不同粒子间会通过协作竞争来逐渐搜索出复杂空间中的最优解[17].
粒子迭代第t次时,其位置信息可用式(9)表示,运动速度用式(10)表示.
Xi(t)=(Xi1(t),Xi2(t),…,Xid(t))(9)
Vi(t)=(Vi1(t),Vi2(t),…,Vid(t))(10)
在每一次迭代过程中,粒子会通过跟踪两个“极值”来不断更新优化自己的速度及位置.其中,跟踪的第一个“极值”即为当前粒子在多维空间中经历的最优值,称为个体极值pBest,用公式表示为:
Pi(t)=(Pi1(t),Pi2(t),…,Pid(t))(11)
而另一个“极值”则是整个种群所有粒子经历的最优值,称为全局极值gBest,用公式表示为:
Pg(t)=(Pg1(t),Pg2(t),…,Pgd(t))(12)
另外,如果将种群一部分作为粒子的邻居而不是全部,那么在该粒子的所有邻居中搜索到的极值则称为局部极值l Best,表示为:
Pl(t)=(Pl1(t),Pl2(t),…,Pld(t)) (13)
粒子迭代更新自身速度和位置公式如下:
Vik(t+1)=ωVik(t)+c1r1(Pik(t)-Xik(t))+
c2r2(Pgk(t)-Xik(t))(14)
Xik(t+1)=Xik(t)+Vik(t+1)(15)
式中:t為当前时刻粒子的迭代次数;ω为粒子的惯性权重系数;c1,c2为学习因子,表示粒子向pBest和gBest运动的加速度权重;r1,r2是介于(0,1)的随机数;k=1,2,…,d.
本文选取模型预测结果的均方误差MSE作为PSO适应度函数,然后通过求解LSSVM模型的最小均方误差来得到最优参数γ,σ2.优化的具体步骤如下:
1)初始化粒子群各参数(学习因子c1=1.5,c2=1.7,最大进化代数maxgen=1 000,种群规模sizepop=30);
2)通过适应度函数计算出各个粒子的适应度值;
3)比较粒子当前适应度值与自身个体最优值pBest,若前者更优,则把粒子当前位置作为目前的个体最优值gBest;
4)对粒子当前适应度值与全局最优值gBest进行比较,若前者更优,则把当前粒子位置作为目前的全局最优值gBest;
5)根据式(14)和式(15)对粒子速度及位置进行更新;
6)判断是否满足结束条件(到达最大循环次数或者误差满足要求),若满足条件则退出循环,否则,回到步骤2)继续循环.
2.2 基于PSO优化的滚动时间窗LSSVM改进算法
基于滚动时间窗的LSSVM回归估计方法的动态建模过程如下:
1)设置各参数初始值;
2)对采集的系统数据进行预处理;
3) 应用PSO优化算法寻优模型参数γ和σ2;
4)选取当前时刻t到(t-q)时刻的样本作为当
前区间时间窗数据;
5)采用基于LSSVM回归估计算法训练模型;
6)利用建立好的模型进行预测;
7)有新数据集进入时,数据窗进行滚动,形成新的时间窗数据;
8)选取新的时间窗数据重新建模并进行预测;
9)返回步骤7).
图2为基于PSO优化的滚动时间窗LSSVM改进算法的基站动态能耗建模流程图.
随着样本数据的更新,上述建模过程循环进行,模型也不断随之更新,这样就能够实时地跟踪基站系统的能耗变化.建模过程中,选取了径向基RBF (Radial Basis Function,RBF)核函数,其中核参数γ和σ2的優化必不可少.γ越小,模型泛化能力越大,平滑性越好,但是拟合能力会降低;同时,σ2越大,所得训练模型就会越平滑,泛化能力也越强.
3 基站能耗预测模型试验仿真
试验样本主要选取2013年1月至2016年1月湖南张家界、邵阳地区某运营商的典型场景基站数据,基本数据类型包括基站每月总耗电量(kW·h)、基站围体面积(m2)、室内外温度(℃)和载频数(个数).基站总耗电量以月·度为单位可以有效过滤由单日能耗异常产生预测偏差的影响,故本文以月·度基站总耗电量为输出,其他变量为输入.同时,以3个月新出现的动态数据作为时间窗数据的更新数据,并随时间不断推移,以更新的时间窗数据作为能耗动态模型的输入数据.
本文采用均方根误差RMSE、相关系数R和决定系数R2 3种评价标准.均方根误差能够很好地反映出预测值的精确度,而相关系数绝对值可以用来反映预测值和实测值关系的方向和密切程度,相关系数绝对值越大,说明预测值和实测值线性关系越好;决定系数为相关系数的平方,能很好的反映模型的拟合程度,其值越接近1,模型的拟合程度越好[18].设Xi为模型预测值,为预测平均值,Yi为对应实测值,为实测值的平均值,其中i=1,2,…,N,定义:
RMSE=1Nσ2∑Ni=1(Xi-Yi)2(16)
R=∑Ni=1(Xi-)(Yi-)∑Ni=1(Xi-)2·∑Ni=1(Yi-)2 (17)
试验所用计算机CPU为AMD Athlon(tm)Ⅱ X2255 Processor 3.10 GHz,内存为4 GB,工具为MATLAB R2011a.将采集的样本数据进行修正和归一化处理后,取前240组数据进行训练模型,后120组数据进行测试.测试结果如图3-图5所示.
对比图3,图4和图5,观察表1可以看出,基于标准LSSVM建立的能耗模型拟合效果较差,而基于PSO-LSSVM和基于滚动时间窗PSO-LSSVM得到的通信基站能耗模型均能够较准确地拟合出能耗的变化,且后两种模型拟合相关系数高,各参数均表现出较好的泛化能力.采用滚动时间窗,可反应系统当前能耗状况的数据快速更新,模型也随之不断更新,从而使得建立的能耗模型更加精确.
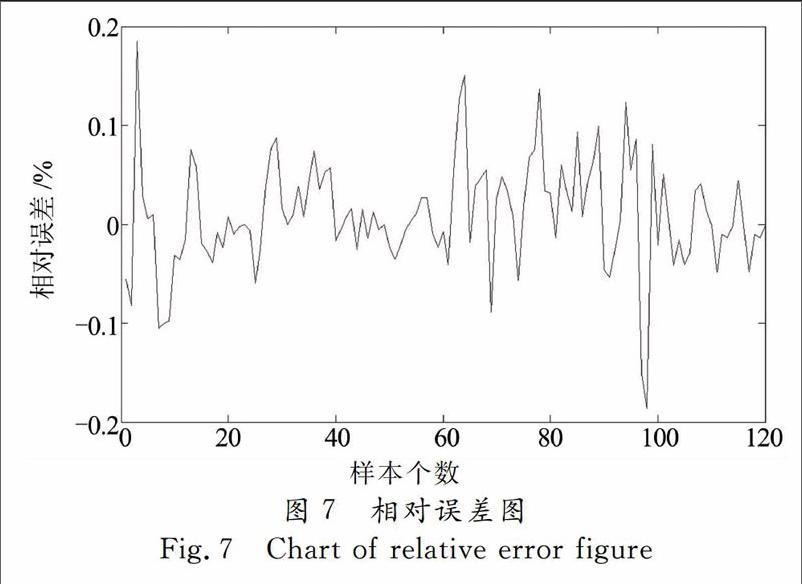
基于测试样本的模型预测效果及误差图分别如图6和图7所示,拟合效果相关参数如表2所示.
从图7可以看出,基站能耗预测误差基本稳定,九成以上的预测值准确度都在90%以内,误差没有随数据变化而较大幅度的增大,而呈现逐步缩小稳定的趋势.从图6,图7和表2可以看出,基站能耗模型能够较好地跟踪实测能耗值的变化趋势,且基站能耗预测精度较高.
目前,通信基站在未采取节能措施的情况下,基于现有文献对通信基站能耗模型的研究,文献[19]采用二元一次线性回归建立了基站能耗模型,其空调耗电模型及设备耗电模型单站试算平均误差分别为18.87%~30.2%及12.32%~19.4%.而文献[7]基于建筑行业的Dest软件模拟建模的预测精度为82%~87%.文献[7]基于Simulink仿真技术建立的动态基站能耗模型仿真精度为86.64%~98.4%.可以看出,在各个不同的典型场景下,基站能耗预测值都普遍不高,虽然文献[7]建立的模型精度偏差不大,但是其超过1/3的能耗预测结果准确度低于90%,其整体预测精度仍然较低.相比来说,本文的研究预测模型整体预测精度更高,使用前景更大.
4 结 论
本文首先综合分析了通信基站总耗电量、主设备耗电量、空调耗电量、电源系统耗电量、外部气象参数变化、室内外气温等数据结构参数,同时,对不同类型典型场景基站的动静态数据进行了采集分析,得到基站能耗与时间、空间、环境参数等数据间的多维关系,计算出影响基站能耗的主要因素,然后,采用基于滚动时间窗的PSO-LSSVM方法建立准确计算基站能耗的多输入复杂系统能耗模型.将该模型与其他相关研究模型的预测精度进行对比,结果表明,本文方法具有更高预测准确度,且整体预测精度在90%以上.综上,本文研究模型具有预测精度较高,稳定性较好等优点,能够更准确地预测通信基站能耗以及更准确地计算节能量,具有良好的应用前景.
参考文献
[1] 张英杰,章兢,刘文强,等.通信行业能耗现状分析与节能战略思考[J]. 电信科学, 2011, 27(10):103-109.
ZHANG Yingjie,ZHANG Jin,LIU Wenqiang,et al.Overview of current state of energy consumption and energy-saving strategies exploration in communication industry[J].Telecommunications Science, 2011, 27(10):103-109.(In Chinese)
[2] LEI F, HU P. A baseline model for office building energy consumption in hot summer and cold winter region[C]//Management and Service Science,MASS '09,International Conference on. IEEE, 2009:1-4.
[3] 戎小寅. 严寒/寒冷地区通信基站动态能耗模拟及围护结构节能优化[D].哈尔滨:哈尔滨工业大学市政环境工程学院,2011:1-19.
RONG Xiaoyin.Dynamic energy simulation and energy efficiency optimization of building envelope for mobile telecommunication base stations in severe cold/cold regions[D].Harbin: School of Municipal and Environmental Engineering,Harbin Institute of Technology, 2011:1-19.(In Chinese)
[4] 周小兵.通信基站节能设计与空调基准耗电量的计算研究[D].长沙:中南大学能源科学与工程学院,2012:1-36.
ZHOU Xiaobin.Study on base stations energy-saving design and air-conditioning baseline power consumption calculation[D].Changsha:School of Energy Science and Engineering,Central South University,2012: 1-36.(In Chinese)
[5] 杨苹,刘胜荣.南方地区移动通信基站的能耗分析与节能评估[J].西华大学学报:自然科学版,2010,29(1):70-73.
YANG Ping,LIU Shengrong.The energy-consuming analysis and energy-saving evaluation of communication base station in South Region of China[J].Journal of Xihua University:Natural Science,2010,29(1):70-73.(In Chinese)
[6] 杨天剑,张静.基于聚类算法的通信基站能耗标杆建立与分析[J].移动通信,2015(18):92-96.
YANG Tianjian,ZHANG Jing.Establishment and analysis of energy consumption benchmark for telecommunication base station based on clustering algorithm[J].Mobile Communications,2015(18):92-96.(In Chinese)
[7] 李阳.基于Simulink仿真技术的基站能耗建模及应用研究[D].北京:北京邮电大学经济管理学院, 2014:1-43.
LI Yang.Study on base station energy consumption modeling and application based on Simulink simulation technology[D]. Beijing:School of Economics and Management in Beijing University of Posts and Telecommunications,2014:1-43.(In Chinese)
[8] VAPNIK V.The nature of statistical learning theory[M].New York: Springer-Verlag,1995:17-21.
[9] 周欣然, 滕召勝. 一种在线稀疏LSSVM及其在系统建模中的应用[J]. 湖南大学学报:自然科学版, 2010, 37(4):37-41.
ZHOU Xinran,TENG Zhaosheng.An online sparse LSSVM and its application in system modeling[J].Journal of Hunan Uniersity:Natural Sciences,2010,37(4):37-41.(In Chinese)
[10]SUYKENS J A K,VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters,1999,9(3):293-300.
[11]AHMADI M A,ROZYN J,LEE M,et al.Estimation of the silica solubility in the superheated steam using LSSVM modeling approach[J]. Environmental Progress & Sustainable Energy,2016,35(2):596-602.
[12]SAFARI H,SHOKROLLAHI A,JAMIALAHMADI M,et al. Prediction of the aqueous solubility of BaSO4 using pitzer ion interaction model and LSSVM algorithm[J]. Fluid Phase Equilibria,2014,374(9):48-62.
[13]阎威武,常俊林,邵惠鹤.基于滚动时间窗的最小二乘支持向量机回归估计方法及仿真[J].上海交通大学学报, 2004, 38(4):524-526.
YAN Weiwu,CHANG Junlin,SHAO Huihe.Least square SVM regression method based on sliding time window and its simulation[J].Journal of Shanghai Jiaotong University,2004,38(4): 524-526.(In Chinese)
[14]孙洁,李辉,韩建光.基于滚动时间窗口支持向量机的财务困境预测动态建模[J].管理工程学报,2010, 24(4):174-180.
SUN Jie,LI Hui,HAN Jianguang.Dynamic financial distress prediction modeling based on rolling time window support vector machine[J]. Journal of Industrial Engineering and Engineering Management, 2010,24(4):174-180.(In Chinese)
[15]KENNEDY J, EBERHART R C. Particle swarm optimization[C]//IEEE International Conference on Neural Networks, 1995, 4(8):1942-1948.
[16]陈志坚, 黄伟杰. 基于多因素混合模型的运营期群桩轴力预测[J]. 湖南大学学报:自然科学版,2016,43(3):155-160.
CHEN Zhijian,HUANG Weijie.Prediction of axial force in pile group during the operation period based on the mixed model of multiple factors[J].Journal of Hunan University:Natural Sciences, 2016,43(3):155-160.(In Chinese)
[17]陈昌富,肖重阳,唐仁华.基于PSO搜索潜在滑裂面非极限状态土压力计算[J]. 湖南大学学报:自然科学版, 2013,40(2):9-14.
CHEN Changfu,XIAO Chongyang,TANG Renhua.Computation of earth pressure under non-limit state based on PSO search of potential slip surface[J].Journal of Hunan University:Natural Sciences, 2013,40(2):9-14.(In Chinese)
[18]王少军,刘琦,彭喜元,等.移动通信话务量多步预测的LSSVM方法研究[J].仪器仪表学报,2011,32(6):1258-1264.
WANG Shaojun,LIU Qi,PENG Xiyuan,et al.Study on LSSVM method for multi-step forecasting of mobile communication traffic[J].Chinese Journal of Scientific Instrument,2011,32(6):1258-1264.(In Chinese)
[19]帥农村,郑辑杰,辛冰,等.GSM移动通信基站能耗模型研究[J].移动通信, 2011, 35(2):87-90.
SHUAI Nongcun,ZHENG Jijie,XIN Bing,et al.Study on GSM mobil communication base station energy consumption model[J]. Mobile Communications,2011,35(2):87-90.(In Chinese)

