滚筒内灰渣表面滚落平均停留时间的模拟及预测

贾建东，　刘汉涛，　苏铁熊,　张培华，　马理强，　樊泽明

(1．中北大学 机械与动力工程学院，太原 030051； 2．中北大学 机电工程学院， 太原 030051；

3．山西平朔煤矸石电厂有限责任公司，山西朔州 036800； 4．中电神头发电有限责任公司，

山西朔州 036013)



滚筒内灰渣表面滚落平均停留时间的模拟及预测

贾建东1，刘汉涛1，苏铁熊2,张培华3，马理强2，樊泽明4

(1．中北大学 机械与动力工程学院，太原 030051； 2．中北大学 机电工程学院， 太原 030051；

3．山西平朔煤矸石电厂有限责任公司，山西朔州 036800； 4．中电神头发电有限责任公司，

山西朔州 036013)

摘要：采用颗粒轨迹模型，考虑灰渣滚落时间，建立了滚筒内灰渣表面滚落过程平均停留时间的数学模型，并与前人的试验数据和模型进行对比验证.采用该模型对滚筒内径、滚筒转速、滚筒倾角α、渣床高度与滚筒内径比h0/R与滚落时间百分比pgun的关系进行预测分析.结果表明：该模型更精确；增大滚筒内径、滚筒转速和滚筒倾角，或减小h0/R值均可使pgun增大，其中滚筒内径和滚筒转速的影响较大.

关键词：滚筒冷渣器； 滚落时间； 颗粒轨迹模型； 平均停留时间； 预测

滚筒冷渣器作为循环流化床(CFB)机组的重要辅机设备，其作用是显而易见的.滚筒内灰渣的运动包括横向和轴向运动，其中轴向运动速率影响冷渣器的出力以及灰渣的轴向扩散[1].滚落状态是灰渣运动的理想状态[2]，在滚落状态下，灰渣截面根据运动特点可分为：(1)底部灰渣随筒体围绕圆心做圆周运动，灰渣间无相对运动，为固定层；(2)渣床表面灰渣从高端随机、无序地自由滑落至低端，为滚落层[3].有关滚筒冷渣器的研究大多针对冷渣器的改造以及传热问题，近几年在传热特性[4]方面的研究很多，而有关灰渣运动特性的研究甚少[5].在灰渣轴向传输方面，庄宇等[3]通过灰渣在滚筒冷渣器内的运动实验，建立了滚筒内灰渣的轴向运动模型，笔者在庄宇等[3]的基础上进一步研究灰渣表面滚落的轴向运动过程，考虑到灰渣颗粒进入滚筒冷渣器入口处具有随机性，以及颗粒滚落时间仍占据一定比重，且不同颗粒的运动时间不同， 在充分考虑这些因素后，通过选取多个灰渣颗粒求取平均停留时间，建立了滚筒内灰渣表面滚落过程平均停留时间的数学模型，并对其中几个重要参数的影响进行了预测分析.

1灰渣滚落时间的随机颗粒轨迹模型

1.1基本假设

颗粒轨迹模型(PTM)最早来自Saeman[6]的单颗粒轨迹几何简化思想.随着学者将随机PTM用来预测滚筒内平均停留时间，随机PTM的思想逐步得到完善，笔者进一步完善其物理思想：

(1) 灰渣在滚筒内的传输过程由固定层的颗粒圆周运动以及渣床表面层的颗粒滚落运动2部分构成的大量重复历程组成.

(2) 单历程中灰渣轴向位移取决于表面层的颗粒滚落运动，与固定层内颗粒圆周运动无关.

(3) 单历程中灰渣的停留时间是其在固定层圆周运动的时间和在表面层滚落时间的总和.

(4) 表面层灰渣颗粒的滚落运动主要受到重力支配，通过对灰渣颗粒轨迹的矢量分析可以求得滚落时间.

(5) 从活动层表面上滚落的颗粒进入非活动层的位置是随机的.

(6) 滚筒冷渣器为稳态运行，灰渣流动处于稳定流动状态，灰渣颗粒为球体，且尺寸均匀.

(7) 不考虑由于颗粒运动不均匀而导致的表面凹凸不平，认为渣床表面平坦；渣床表面沿横向方向为平面，沿轴向渣床厚度一致.

对于滚筒冷渣器灰渣运动的研究，庄宇等[3]认为灰渣颗粒的滚落时间可以忽略，并且未考虑颗粒运动的随机性，笔者完善了其物理思想，充分考虑了颗粒运动的随机性和滚落时间.

1.2单颗粒相关参数的计算

在如图1所示的滚筒冷渣器上建立直角坐标系，坐标原点位于滚筒入口渣床中心，x轴平行于渣床表面，y轴垂直于渣床表面，z轴与渣床平面中心线重合.图中，ω为滚筒转速.

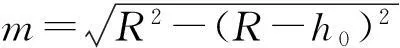
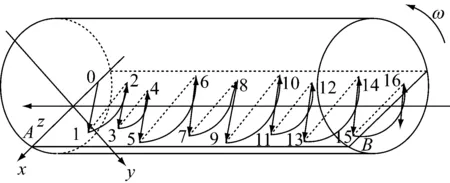
图1　单颗粒运动轨迹

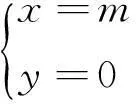
(1)

设灰渣进入滚筒的起始点为D(x0,y0,z0)，其轴向和径向位置是确定的，分别为y0=R-h0，z0=0，而横向位置是一个随机数，满足均匀分布：

x0=m·unifrnd(-1,1)

(2)

任意点c为起始点的灰渣在横截面的运动轨迹如图2所示，令c点坐标为c(xc，yc，zc)，那么可求出b点坐标为：

(3)

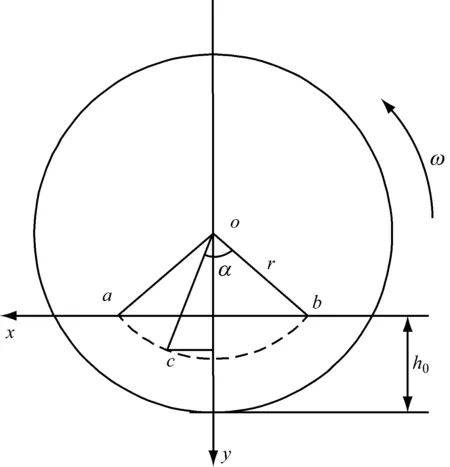
图2　灰渣在横截面的运动轨迹

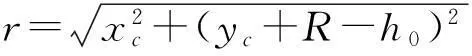
灰渣单次滚落位移与z轴分位移的夹角为φ,则灰渣表面滚落的轨迹方程为：(x-x0)tanφ=z-z0，对于螺旋肋板：tanφ=螺距/内筒周长[3].直线AB与灰渣滚落轨迹所在直线的交点F的坐标为(m，0，(xF-x0)tanφ+z0).由于灰渣颗粒之间存在摩擦和碰撞，灰渣进入固定层的位置是随机的，在直线OF上随机的某点.根据灰渣的运动特性，灰渣进入固定层的概率分布满足：令x/xF=η，0≤η≤1，则概率密度函数为f(η)=2η.所以，如果滚落层灰渣从G点进入固定层，则G点坐标为：(η·xF,0,(η·xF-x0)tanφ+z0).

灰渣在单次滚落过程中的轴向移动距离d=zG-z0，根据重力矢量分析[7]，可知灰渣颗粒在z轴方向的受力加速度为gsinα，其中α为滚筒倾角，则灰渣颗粒单次滚落时间为：

(4)

经过多个重复历程，直到灰渣颗粒z轴坐标值大于滚筒长度L时，说明灰渣从出口排出，结束迭代过程，则累加的圆周运动时间和滚落时间的总和即为单颗粒在滚筒内的停留时间.

1.3颗粒群平均停留时间的计算

设颗粒群里包括N个灰渣颗粒，由于滚落过程存在随机性，计算得到的滚落时间和圆周运动时间均呈现随机性，从而整个停留时间也呈现随机性.因此，在计算平均停留时间时，需要对单个颗粒停留时间进行统计分析.因此，

(5)

(6)

为了更清晰地描述灰渣颗粒滚落过程中滚落时间在全过程中所占的比重，引入滚落时间百分比的概念：

(7)

2模型计算及验证

灰渣颗粒平均停留时间的计算过程可以用图3的流程图表示.

庄宇等[3]搭建了滚筒冷渣器实验台，滚筒内装有8根纵肋，均匀布置在滚筒内壁面，滚筒总长度为4 m，实际停留时间测定的有效长度为2 m，外径为0.8 m，壁厚为0.01 m，出口挡板高度为0.06 m，实验采用石英砂代替灰渣，平均粒径为0.428 mm，堆积密度为1 456 kg/m3，真实密度为2 520 kg/m3，灰渣堆积角为40°.笔者所建模型采用文献[3]的实验结果进行验证，并与文献[3]、文献[7]～文献[9]的计算结果进行比较，结果如表1所示.

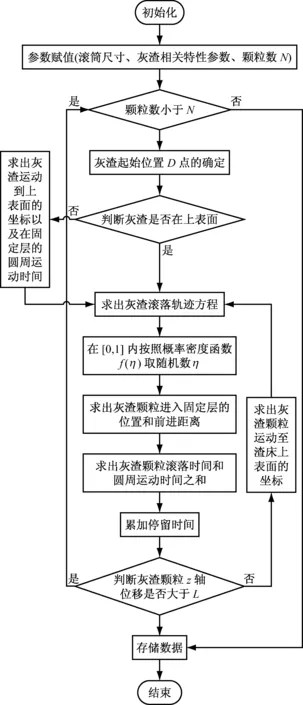
图3　灰渣颗粒平均停留时间计算流程图

由表1可知，该模型模拟值普遍更接近真实值，在滚筒转速为4.96 r/min时误差较大，这是由于在滚筒转速较高时，灰渣的填充率降低，导致肋板对灰渣的抛洒作用加大，被抛洒的灰渣颗粒平均停留时间增加，模拟计算并未考虑抛洒作用对平均停留时间的影响，所以模拟值误差偏大；在滚筒转速为1.82 r/min、滚筒倾角为1.5°时，渣床高度较高，此时渣床高度在z轴方向并不能认为是不变的，模型忽略了渣床高度的变化，因而所求出的模拟值大于实验值，误差较大；而其他情况下，模拟值误差均小于7%.因此，该模型对于填充率较小、滚筒转速较低的情况较准确.

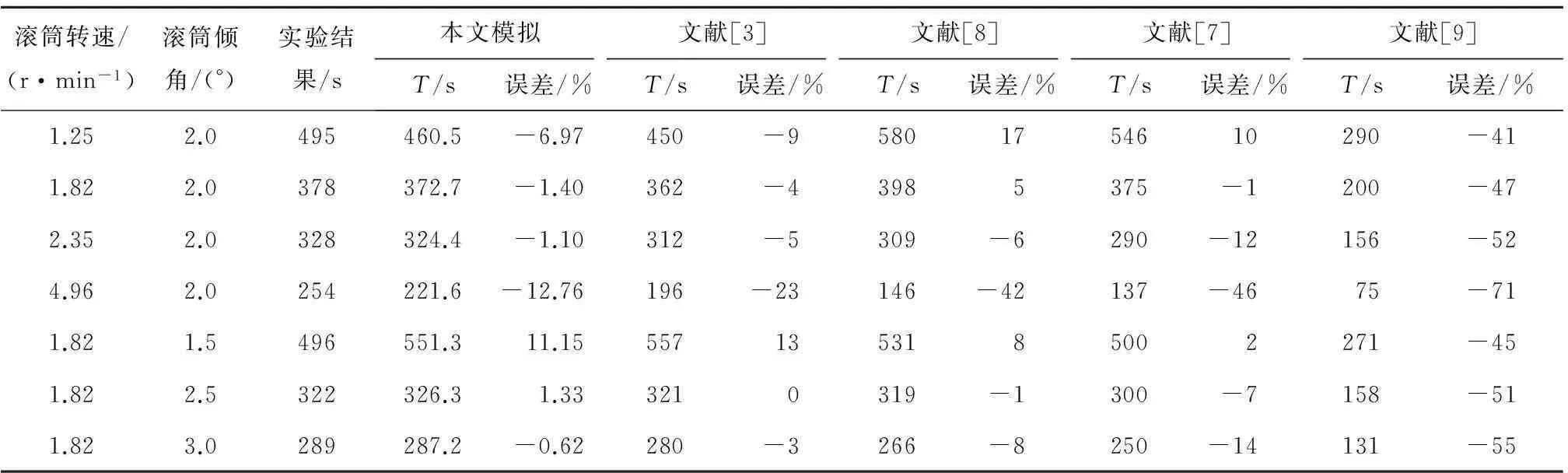
表1　平均停留时间实验与模拟结果的比较

3影响因素预测

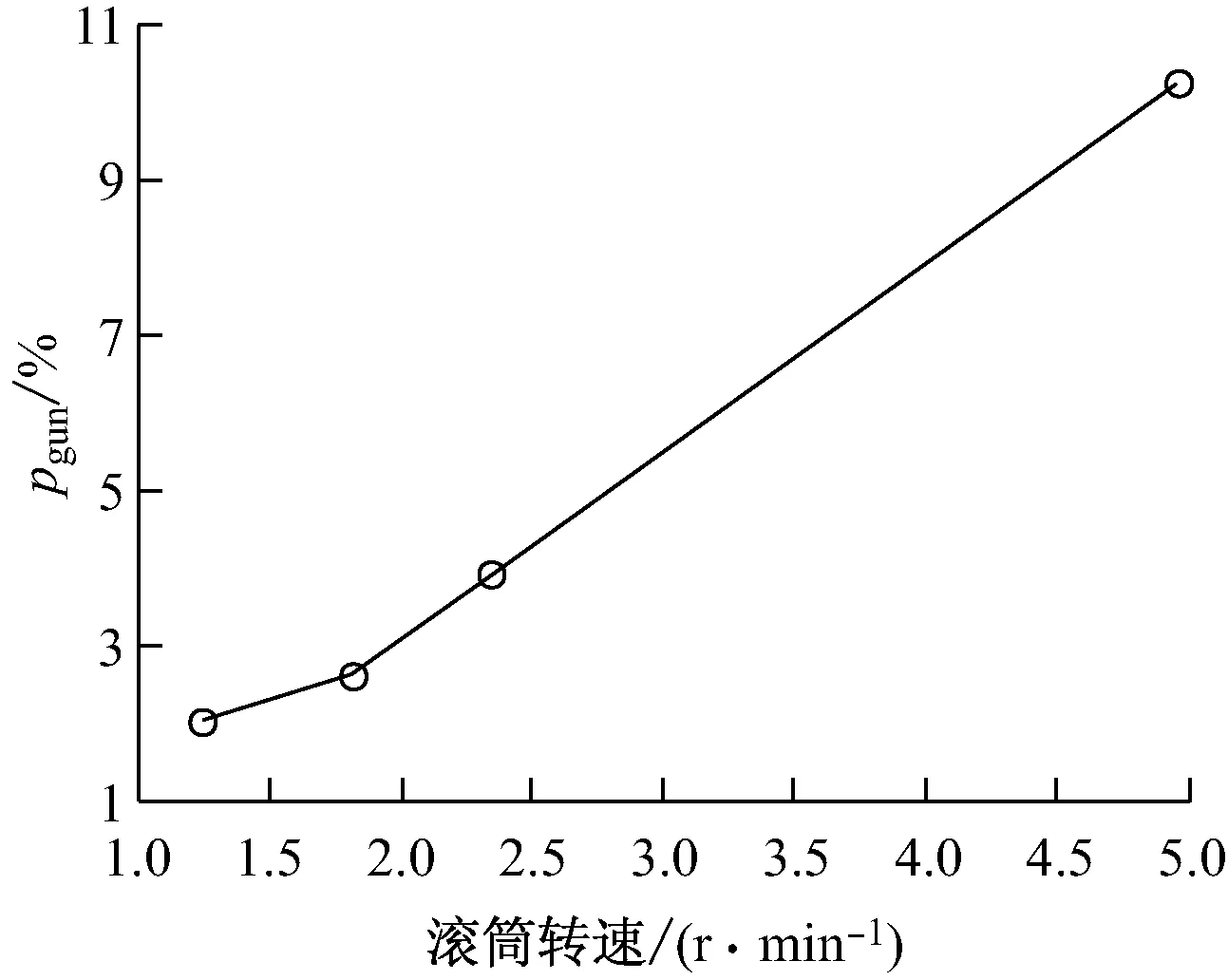
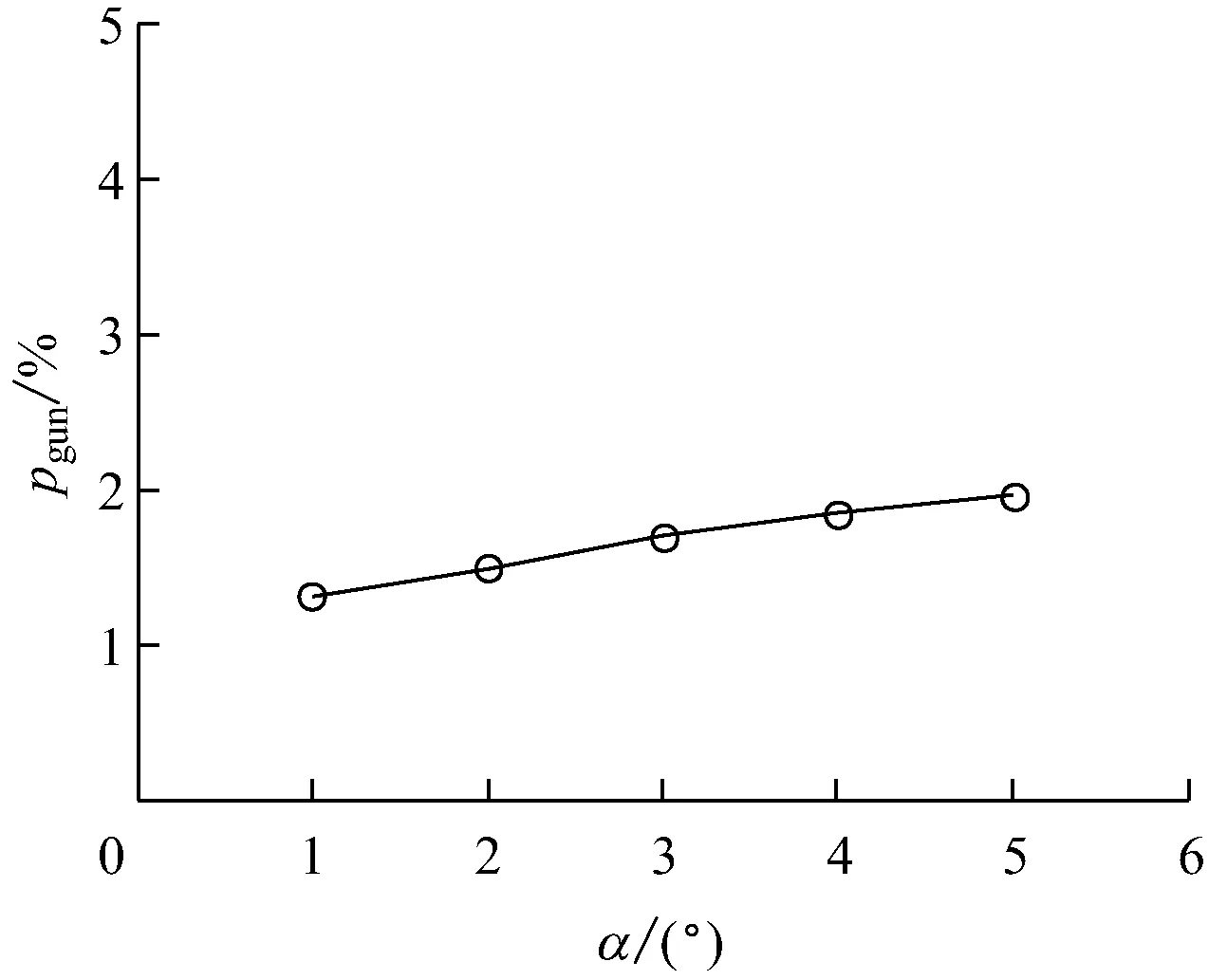
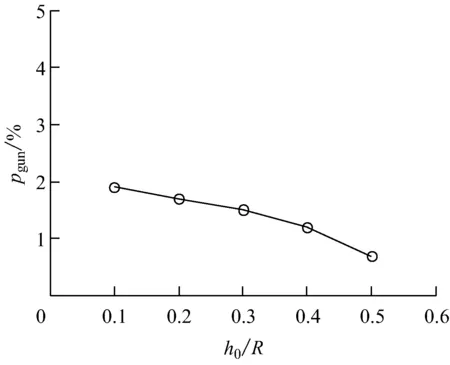
令模型其他参数不变，仅改变几个重要参数进行预测，如滚筒内径R、滚筒转速、滚筒倾角α、渣床高度与滚筒内径比h0/R.图4给出了这4个参数变化对滚落时间百分比的影响.

由图4可知，在其他因素不变的情况下，随着滚筒内径的增大，pgun增大，这是由于滚筒内灰渣的填充率降低，使得灰渣运动到渣床表面进行轴向传输的概率增加；滚筒转速增大时，pgun与滚筒转速基本呈线性关系，滚筒转速的增大会使灰渣颗粒在固定层的圆周运动时间缩短，相对而言，在表面层的滚落时间增加，同时也会使滚筒内存渣量减少，从而降低灰渣的填充率，使得pgun增大；滚筒倾角α的变化也会使pgun变化，但影响不大，随着α的增大，滚筒内存渣量减少，使得pgun增大；渣床高度与滚筒内径比增大，导致滚筒内灰渣的填充率增大，从而延长了灰渣的圆周运动时间，缩短了滚落时间，使得pgun减小.

总之，增大滚筒内径、滚筒转速和滚筒倾角，或减小渣床高度与滚筒内径比，均可使pgun增大，其中滚筒内径和滚筒转速的影响较大.

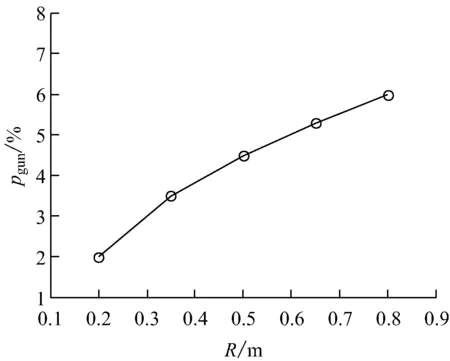
(a) 滚筒内径与pgun的关系

(b) 滚筒转速与pgun的关系

(c) 滚筒倾角与pgun的关系

(d) 渣床高度与滚筒内径比与pgun的关系

4结论

(1) 所建数学模型较其他模型更为精确，尤其是在填充率较小、转速较低的情况下具有较高的精确度.

(2) 滚筒内径增大使得滚落时间百分比增大，其对滚落时间百分比的影响较大；滚筒倾角、渣床高度与滚筒内径比的变化对滚落时间百分比的影响较小，可以忽略；滚筒转速与滚落时间百分比基本呈线性变化，即滚筒内径增大使得滚落时间百分比增大，对滚落时间百分比有较大影响.

参考文献：

[1]曲航，赵军，刘晓燕．回转窑内滚动状态下颗粒横向运动的影响因素的实验研究[J]．硅酸盐通报，2007，26(3)：441-446．

QU Hang, ZHAO Jun, LIU Xiaoyan. Experimental study on the influence factors of transverse motion of particle at rolling regime in the rotary kiln[J].Bulletin of the Chinese Ceramic Society, 2007,26(3):441-446.

[2]MELLMANN J,SPECHT E,LIU X. Prediction of rolling bed motion in rotating cylinders[J].AIChE Journal,2004,50(11): 2783-2793.

[3]庄宇，陈汉平，王贤华,等．滚筒式冷渣器灰渣运动实验与模拟[J]．热能动力工程，2012，27(2)：218-221．

ZHUANG Yu,CHEN Hanping,WANG Xianhua,etal. Experimental and simulation study of the ash and slag movement in a roller type slag cooler[J]. Journal of Engineering for Thermal Energy & Power, 2012,27(2):218-221.

[4]司小东,吕俊复,王巍,等.滚筒冷渣器传热模型的研究[J].动力工程学报,2011,31(5):342-346.

SI Xiaodong, LÜ Junfu,WANG Wei,etal.Research of heat transfer model in rotary ash coolers[J]. Journal of Chinese Society of Power Engineering, 2011,31(5):342-346.

[5]刘柏谦.连续雪崩式对流冲刷传热滚筒冷渣器：中国， CN201120493763[P].2012-10-10．

[6]BOATENG A A, BARR P V. Modeling of particle mixing and segregation in the transverse plane of a rotary kiln[J].Chemical Engineering Science,1996,51(17): 4167-4181.

[7]LI S Q, CHI Y, LI R D,etal.Axial transport and residence time of MSW in rotary kilns: Part II.Theoretical and optimal analyses[J]. Powder Technology，2002,126(3):228-240.

[8]SULLIVAN J, MAIER C, RALSTON O.Passage of solid particles through rotary cylindrical kilns[M]. Washington, USA: US Government Printing Office,1927.

[9]CHATTERJEE A, SATHE A, MUKHOPADHYAY P. Flow of materials in rotary kilns used for sponge iron manufacture:Part II.Effect of kiln geometry[J].Metallurgical and Materials Transactions B,1983, 14(3):383-392.

Prediction on Mean Residence Time of Ash Particles Rolling Down the Surface of a Rotary Ash Cooler

JIAJiandong1,LIUHantao1,SUTiexiong2,ZHANGPeihua3,MALiqiang2,FANZeming4

(1.School of Mechanical and Power Engineering, North University of China, Taiyuan 030051, China;2. School of Mechatronic Engineering, North University of China, Taiyuan 030051, China;3. Shanxi Pingshuo Gangue-fired Power Generation Co., Ltd., Shuozhou 036800, Shanxi Province,China; 4. CPI Shentou Power Generation Co. Ltd., Shuozhou 036013, Shanxi Province, China)

Abstract：Using the particle trajectory model and considering the slag fall time, a mathematical model was established for the mean residence time of ash particles rolling down the surface of a rotary ash cooler, which was compared and verified with previous models and experimental data. The model was used to analyze the effects of following factors on the pgun, such as the drum diameter, the roller speed, the roller angle, and the ratio of slag bed height to drum diameter h0/R, etc. Results show that the model is more accurate and the pguncan be improved by increasing the drum diameter, the roller speed and the roller angle, and by reducing the value of h0/R, in which the drum diameter and roller speed have great influence.

Key words：rotary ash cooler; fall time; particle trajectory model; mean residence time; prediction

文章编号：1674-7607(2016)03-0213-05

中图分类号：TK223.28

文献标志码：A学科分类号：470.30

作者简介：贾建东(1990-)，男，山西大同人，硕士研究生，主要从事滚筒冷渣器灰渣运动与传热的分析研究.电话(Tel.):18234060756；

基金项目：山西省科技攻关资助项目(20140321022-02)；朔州市科技攻关资助项目(2013-33-38，2013-33-40)

收稿日期：2015-05-11

修订日期：2015-07-21

E-mail：1070660903@qq.com.