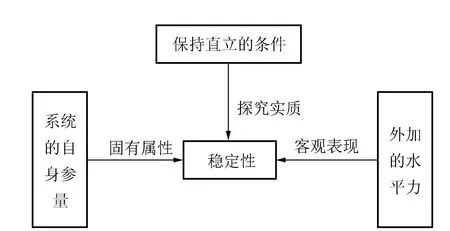
不倒塔的实验探究

李可妤，徐 蕾，钟 鸣

(南京师范大学 物理科学与技术学院，江苏 南京 210023)

在演示平衡和惯性的实验中，有一类非常有趣的实验，例如，把硬币一个个叠起，看看谁能使叠的硬币伸出底面最多？把硬币堆叠成直立的塔，快速击打最下层的硬币，看看谁能保证上层的塔不倒？在有趣的实验现象和定性解释背后，保持平衡的条件究竟和哪些因素有关，值得更为深入的探讨. 为此，设计了不倒塔的实验装置，通过实验进行定量探究.

1 实验设计与原理

1.1 实验装置设计

首先搭建整体装置，把几个相同的圆盘上下整齐地叠放在桌面上，形成直立的塔. 考虑到直接击打较难准确控制力的大小、方向以及作用时间，采用了替代方法：将轻绳一端连接重物瓶，穿过定滑轮后连接到最底层的圆盘上,如图1所示.

图1 实验装置示意图

通过突然释放重物瓶来等效替代击打最底层的圆盘，可以通过改变重物瓶的质量以改变突然施加的水平力的大小，降低测量的难度，保证可重复性.

1.2 实验现象

在实验中可以观察到，当塔层形状相同时，改变瓶中重物的质量会影响最下层塔抽出的时间，进而影响塔是否能够保持直立不倒. 当外加水平力越大，抽取时间越短，上方的塔身受到的影响就越小，塔越能保持稳定.

以地面为参考系，建立二维平面xy坐标系，其中x方向为水平方向，y方向为竖直方向. 标记每层塔的中心位置，拍摄实验视频，采用Tracker软件记录数据，对层数为4的塔的整体运动情况进行分析.

图2为各圆盘的x和y方向的位移随时间的变化情况. 由图2可以看出，在x方向上，同一塔中各个圆盘最终会发生错位，低层的圆盘x方向的位移更大；在y方向上，曲线前段较光滑部分表示自由下落过程，后由于碰撞地面引起微小扰动.

1.3 原理分析

将最下面的圆盘称为底层圆盘,上面的圆盘整体称为塔身，并且对塔身的每个圆盘从下到上进行编号1，2…N. 将塔的运动过程分为3个阶段：接触阶段、自由下落阶段和碰撞阶段，接下来将分阶段描述塔的运动情况.

(a)x方向位移

(b)y方向位移图2 x和y方向塔的整体运动情况图

1.3.1 接触阶段

接触阶段从突然施加的水平力作用于底层圆盘开始，到塔身脱离最底层圆盘结束，构成塔身的圆盘彼此之间没有相对位移，塔身可视为刚体. 这一阶段又分为2个过程，如图3所示.

(a) (b)图3 接触阶段示意图

1)当底层圆盘与塔身脱离距离小于圆盘半径R，塔身不发生倾斜. 底层圆盘受到的力有重力、塔身给予的摩擦力与压力、桌面给予的支持力与摩擦力；塔身受到的力有重力、底层圆盘给予的支持力与摩擦力.

底层圆盘的水平方向运动方程为

(1)

塔身作为整体(刚体)的运动方程为

(2)

其中，m为单个圆盘的质量，R为圆盘半径，M为悬挂重物的质量，x底为底层圆盘的x方向位移，x塔为塔身的x方向整体位移，μ为圆盘与圆盘之间的摩擦因数，μ0为底层圆盘与桌面的摩擦因数.

2)当底层圆盘与塔身脱离距离大于半径R，此时塔身会绕着接触点进行转动. 在实验过程中，倾斜角度较小，并且这一过程持续时间较短，因此，可以近似认为底层圆盘的受力恒定，此时底层圆盘的运动方程仍为式(1)，塔身的运动为平动与绕接触点的转动的合成，平动的运动方程仍为式(2). 绕接触点的转动方程为[1]

(3)

其中，J为转动惯量，θ为倾斜角度，h为单个圆盘高度，其值为

(4)

其中Δx表示接触点到塔身底边中点的距离，满足以下条件：

(5)

1.3.2 自由下落阶段

自由下落阶段如图4所示，从塔身与地面脱离为开始，到塔身触碰地面结束. 塔身只受到重力作用，作为整体进行运动. 将这一运动进行分解，可以分为质心的抛体运动与整体绕质心轴的转动. 并且转动的初始角速度ω来自接触阶段，在自由下落阶段，质心轴合力矩为0，因此是角速度为ω的匀角速转动. 用Δy表示圆盘下端离地面的竖直距离，满足以下方程：

图4 自由下落阶段示意图

(6)

其中，θ0为初始倾斜角度，φ为其余圆盘的对角，即

(7)

1.3.3 碰撞阶段

碰撞阶段从塔身接触地面开始，到塔身部分的各个圆盘相对地面静止结束. 由于碰撞等复杂的运动，最后塔身部分的各个圆盘会在x方向上产生错位，如图5所示. 当圆盘间相对位移在一定范围内，塔不会倒塌；当相对位移超出某一临界值时，塔会倒塌. 而关于这一临界判断条件，将在后面进行讨论.

(a)碰撞地面 (b)最终状态图5 碰撞阶段示意图

碰撞阶段初始时的各个圆盘的速度：

(8)

(9)

其中，θ落为塔身刚落到地上的倾斜角度，n为第n个圆盘的编码，N为塔身的总圆盘个数.vx，vy分别为整体运动时质心的速度，经历前2个阶段之后其值分别为

(10)

vy=gt阶段2,

(11)

碰撞到地面后，各个圆盘的速度与碰撞系数有关[2]：

vny=vny初[en-1e0-eN-n],

(12)

(13)

其中，e为圆盘之间的碰撞系数，e0为圆盘与地面间的碰撞系数.

自接触地面开始，各圆盘均以下端接触地面的点为转轴，完全落地后可认为倾斜角度约等于落地瞬间整体的倾角，各层圆盘在x方向产生的位移为

(14)

与地面碰撞后x方向产生位移为

(15)

落地后仅有x轴方向的运动，塔层间相互锁定，受摩擦力作用直到vnx=0,

(16)

圆盘之间最终的相对位移为[3]：

xn=xn1+xn2+xn3.

(17)

1.3.4 塔是否倒塌的判据

显然，当圆盘间相对位移在一定范围内，塔不会倒塌；当相对位移超出某一临界值时，塔会倒塌. 接下来根据堆塔原理(图6)建立塔是否倒塌的判断函数[4-8].

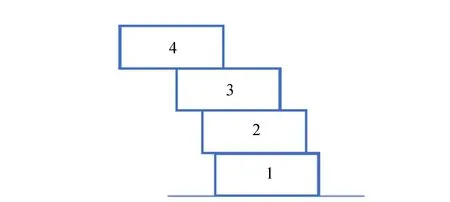
图6 堆塔原理示意图

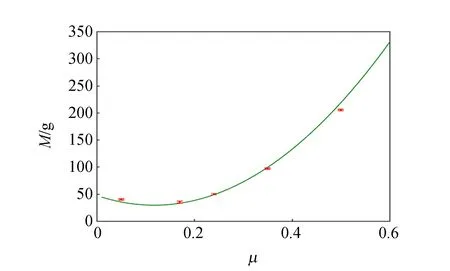
xcN-n-xn

(18)

(19)

同时满足这2个条件，塔不会倒塌.

通过以上分析，可以用Matlab对运动的3个阶段进行数值模拟，最终将实验结果和数值模拟结合，得到相关参量和塔稳定性之间的关系.

2 实验探究

2.1 实验器材

器材包括电子天平、定滑轮、鱼线、重物瓶、小圆珠、不同规格的亚克力圆盘以及不同粗糙程度的磨砂纸，如图7所示.

(a)实验装置 (b)不同规格的亚克力圆盘图7 实验器材图

2.2 对影响塔稳定性相关参量进行实验探究

根据上述理论分析，设计了一系列控制变量实验，分别改变圆盘的层数N、圆盘的半径R、单个圆盘的高度h、圆盘与地面间的摩擦因数μ0以及圆盘间的摩擦因数μ，探究影响塔保持直立的条件，如图8所示.

图8 相关参量图例

2.2.1 圆盘层数N和塔稳定性的关系

采用R=1.5 cm，h=1.5 cm的圆盘进行实验，其他条件不变，改变圆盘的层数. 可以看出随着塔层数的增加，需要施加悬挂物的临界质量呈上升趋势. 即层数越大，所需悬挂物的质量越大才能保证塔不倒塌，层数越高的塔越不稳定. 在实验中还发现，当N=7时，所需悬挂物的临界质量会骤然增加，这是由于层数的增大，圆盘间的相互影响会导致更大的不稳定性.

图9(b)中绿线为Matlab模拟的结果，取0.01为步长，通过数值计算得到临界的质量，与实验进行对比，可以看出模拟和实验结果符合得很好. 而对于任意一组控制变量实验，使用的悬挂物的质量最小为1.5 g，通过不断增加悬挂物的质量来寻找能够使塔不倒的临界质量.

(a)实验结果图

(b)模拟和实验对比图图9 圆盘层数和塔稳定性关系

2.2.2 圆盘的半径R和塔稳定性的关系

采用层数为4层，h=1.5 cm的圆盘进行实验，其他条件不变，改变圆盘的半径R,实验曲线如图10所示. 实验发现，当圆盘半径在一定范围内时，圆盘的半径越大，需要施加悬挂物的临界质量呈下降趋势，即半径越大塔越稳定；但当半径超过某一临界值时，抽出底层圆盘的位移变大，抽出时间也会越长，需要施加悬挂物的临界质量呈上升趋势，塔越难以保持直立，稳定性越差. 也就是说圆盘存在最优半径，模拟结果显示其最优值为2.15 cm. 当半径超过最优值时，其余圆盘与底部圆盘的的接触时间增加，其获得的角速度与倾斜角度增大，塔难以保持直立.

图10 圆盘半径和塔稳定性关系的模拟和实验对比图

2.2.3 单个圆盘高度h和塔稳定性的关系

采用层数为4层，R=1.5 cm的圆盘进行实验，其他条件不变，改变圆盘的高度h，实验图像如图11所示. 可以看出随着单个圆盘高度的增加，需要施加悬挂物的临界质量呈上升趋势. 即单个圆盘高度越高的塔越不稳定. 从定性的角度分析，塔重心越高越不稳定，因此需要更大的临界质量来缩减对其余圆盘的影响时间.

图11 单个圆盘高度和塔稳定性关系的模拟和实验对比图

2.2.4 圆盘与地面间的摩擦因数μ0和塔稳定性的关系

控制其余变量不变，仅改变圆盘与地面接触面的摩擦因数μ0，实验图像如图12所示. 发现圆盘与地面间的摩擦因数μ0越小，所需施加悬挂物的临界值量就越小，塔稳定性越好. 从这一实验看，地面的摩擦因数对塔产生的是负影响. 由于摩擦力的增大，为了控制抽取时间，所需的临界质量也会相应增大.

2.2.5 圆盘间的摩擦因数μ和塔稳定性的关系

控制其余变量不变，仅改变上层圆盘间的摩擦因数μ，实验图像如图13所示. 可以发现，在一定范围内时，圆盘间的摩擦因数越大，需要施加悬挂物的临界质量呈下降趋势；当摩擦因数超过某一临界值时，需要施加悬挂物的临界质量又会增加. 考虑到摩擦因数较小，导致在第三阶段塔层间相互锁定时，vnx需要较长时间才能减为0，圆盘间的相对位移反而超过堆塔原理所要求的临界距离，导致塔更加难以保持不倒.

图12 圆盘和地面间摩擦因数和塔稳定性关系的模拟和实验对比图

图13 圆盘间摩擦因数和塔稳定性关系的模拟和实验对比图

3 实验结论

从实验可以得出，塔保持不倒的原因是用突然的水平力抽取底层圆盘后，导致塔身各个圆盘之间产生相对位移,当相对位移处在堆塔原理限制的塔层间最大伸出距离以内，塔可以保持直立.

采用模拟与实验相结合的方法，从影响塔的稳定性的因素出发，探究了塔的保持直立的条件，得到主要结论如下：

1)不利的影响因素有塔的层数、单个圆盘的高度、圆盘与地面的摩擦因数. 塔的层数越大、圆盘的高度越高、圆盘与地面的摩擦因数越大，塔越不稳定；

2)圆盘的半径对于塔保持直立的影响存在最优的值，这时塔的稳定性最好；

3)圆盘间的摩擦因数对于塔保持直立的影响也不是单一的，在一定范围内时，圆盘间的摩擦因数越大，塔的稳定性越好，当超过某一临界值时，塔越不稳定.

4 总结与反思

本文对一个典型的力学问题进行探究，通过给底层圆盘施加突然的水平力这一外在客观表现来观察塔自身的稳定性情况，基本思想是从预实验中塔的整体运动规律出发→分解各个阶段的运动过程→得出最终状态圆盘之间横向位移的关系→通过判断函数得出塔是否能保持直立→正式实验进行验证. 实验采用的描述方法如图14所示.

图14 实验描述方法

本文在实验理论上进行了一定的简化，在此仅给出了主要影响参量的实验结果，而对于其他的影响因素，如碰撞系数等，因实验表面所用材质相同而近似认为碰撞系数不变，在该实验中作为无关变量进行控制.