基于拓扑光子晶体的新型光波导研究
陈晓东,何辛涛,董建文
(中山大学 物理学院,广东 广州 510275)
随着云计算、三维全息、移动通讯等新型技术的迅速发展,对信息获取、传输、处理、储存的要求也越来越高. 光具有工作频带宽、传输速度快、信息载量大等优点,人们希望像控制电子一样控制光,实现精准光场调控,使光成为下一代信息的载体. 其中作为代表性的光学结构,光子晶体由于其独特的光学性质受到国内外研究者的广泛关注. 通过光子能带“剪裁”,光子晶体不仅可以实现诸如超棱镜、负折射、隐身传输等新型光场调控[1-3],而且可以实现高效光波导、低阈值激光器等新型光子器件[4-6],已经成为基础光物理探索和前沿光子学应用的重要研究体系之一. 然而,随着片上微纳制备技术的发展,基于光子晶体的光子器件变得越来越小,制备过程中错位、缺陷等不可控因素引起了较大散射损耗,严重制约了光子器件的进一步发展. 近年来,研究者将拓扑原理引入到光学领域,实现了拓扑光子晶体,发现了单向传输、抗散射传输等新型光场调控现象[7-8],为光波导等集成光子器件设计提供了新思路[9-10]. 本文首先介绍了拓扑光子晶体的基本概念,然后从拓扑光子晶体发展历程出发介绍了3种典型的拓扑光子晶体的理论原理与实验方案,最后介绍了新型光波导的结构设计和性能表征.
1 拓扑光子晶体基本概念
光子晶体是20世纪80年代末提出的具有周期性的光学结构,具有光子禁带,支持光子局域态,可以实现慢光传输等新型光传播行为,受到研究者的广泛关注[11-12]. 按照光子晶体物质参量的周期性空间分布,光子晶体可以分成一维、二维和三维光子晶体(图1).

(a)一维 (b)二维 (c)三维图1 光子晶体示意图
光在光子晶体中传播时受周期性变化物质材料参量调制而发生布洛赫散射,散射波之间形成干涉,最终在倒格矢空间中形成光子能带. 以晶格常量为a的二维正方光子晶体为例,原胞中心是直径为0.68a、折射率为3.4的介质圆柱,而背景材料折射率为1. 该光子晶体的光子能带如图2所示,其中红色和蓝色曲线分别标出了横电和横磁模式的光子能带. 光子晶体的拓扑属性由光子能带上本征模式对应的拓扑不变量表征. 例如,旋电光子晶体和磁性光子晶体等时间反演对称破缺拓扑光子晶体,表征它们拓扑属性的拓扑不变量是陈数,其定义为
其中F(k)=k×A(k)是贝里曲率,k是倒格矢空间中的波矢,A(k)=〈u(k)|ik|u(k)〉是贝里联络,ik是倒格矢空间中的厄米共轭算符,u(k)是光子晶体电磁场分布的空间周期性变化项,〈…〉作用在光子晶体实空间上.

图2 二维正方格子全介质光子晶体的横电和横磁模式能带以及本征横磁模式的电场Ez分布
由拓扑学原理可知,表征空间拓扑属性的拓扑不变量对连续微扰不敏感. 所以当光子晶体材料参量发生微扰时,能带的陈数不会发生变化,相应禁带的禁带陈数也不会发生改变. 只有当2条光子能带在某些高对称波矢上发生重叠,能带上本征模式发生交换,禁带出现闭合又重新打开的情况后,禁带拓扑属性才会改变. 禁带拓扑属性发生变化的前后,分别对应2种拓扑属性不同的光子晶体. 由于2个光子晶体的禁带的拓扑属性不同,所以在它们的界面上必然会发生拓扑相变. 这要求边界上禁带发生闭合,从而保证了边界上存在无带隙边界态. 无带隙是指边界态的频率会覆盖整个禁带频率. 无带隙边界态受拓扑保护,无需特殊调整边界形貌,普遍存在于拓扑属性不同的光子晶体边界上. 由于这类边界态具有特殊性质(如单向传输和抗散射传输等),所以研究者可以利用该边界态实现某种新型光波导.
2 磁性光子晶体与单向光传输
如何实现拓扑不变量非零的光子晶体是实现拓扑光子晶体需要解决的重要问题. 2008年,美国普林斯顿大学F.D.M. Haldane和S. Raghu在旋电光子晶体中发现了陈数非零的拓扑光子晶体[13]. 三角格子光子晶体利用晶格对称性,在布里渊区角落K点附近可以实现线性狄拉克锥能带,即第2和第3能带在布里渊区边界波矢K点上发生简并. 通过外加沿z方向的电场,旋电材料结构的时间反演对称性被打破,原本能带的简并会被打开,从而获得全向光子禁带. 特别是,由于时间反演对称性破缺而分离的第2和第3能带的陈数非零,两能带之间的禁带陈数非零,属于拓扑非平庸光子禁带. 至此,利用时间反演对称性破缺的旋电光子晶体可以实现拓扑非平庸的拓扑光子晶体.

图3 二维正方格子磁性光子晶体的横磁模式能带图

图4 陈数非零的磁性光子晶体边界上的单向传输边界态
由于无带隙边界态的单向传输和后向散射免疫的稳定传输特性,可以实现支持单向传输模式的波导,磁性光子晶体引起研究者的广泛兴趣. 南京大学和香港科技大学研究组实现了蜂窝状磁性光子晶体,该结构的边界态直接存在于磁性光子晶体与空气的边界上,无需外加完美电导体形成边界[16-17]. 中国科学研究院物理所研究组在磁性光子晶体中实现了抗散射和微扰免疫的磁性可调单向波导[18]. 美国麻省理工大学Scott A. Skirlo等通过理论和实验获得大禁带陈数的波导,实现了高耦合效率的多模波导[19].
3 电磁对偶光子晶体与赝自旋单向光传输
尽管旋电光子晶体或者磁性光子晶体非平庸拓扑禁带中无带隙边界态有很好的光学性质,但是由于光波段磁性材料的缺失制约该拓扑光子晶体的进一步发展. 制约其发展的根本物理原因是该系统需要打破时间反演对称性来获得非零陈数,从而实现拓扑非平庸禁带. 那么能否在时间反演对称的光学系统中实现由其他非零拓扑不变量表征的非平庸禁带呢?答案是肯定的[20-24]. 一方面需要引入赝自旋,即相互正交的2个偏振模式. 另一方面需要引入赝自旋-轨道耦合,等效于打破某种赝自旋的时间反演对称性,使赝自旋单向传输. 2013年,美国德州大学奥斯丁分校G. Shvets研究组在双各向异性特异材料中实现了禁带自旋陈数非零的拓扑非平庸禁带[20]. 对于二维三角格子光子晶体(图5),其组成材料满足电磁对偶条件,即所有材料的介电常量和磁导率的比值为恒定值. 在这样的电磁对偶体系中可以构建赝自旋态,其中赝自旋向上态对应电场和磁场同相,而赝自旋向下态对应电场和磁场反相. 同时为了引入赝自旋-轨道耦合,材料需具有双各向异性,即电位移矢量D和磁感应强度B均与电场E和磁场H相关. 基于电磁对偶和非零双各向异性系数条件,双重简并狄拉克锥会被打开,从而形成禁带自旋陈数非零的拓扑非平庸禁带.
该禁带自旋陈数非零的拓扑非平庸禁带支持单向传输的赝自旋态. 如图6所示,当输入源放置在波导左端时,激发的电场Ez和磁场Hz同相,即只有单向向右传输的赝自旋向上态被激发. 相反,当输入源放置在波导右端时,激发的电场Ez和磁场Hz反相,即只有单向向左传输的赝自旋向下态被激发. 数值模拟结果表明单向传输的赝自旋边界态同样具有抗散射传输性质,对挖空、扰动等缺陷均具有鲁棒性.
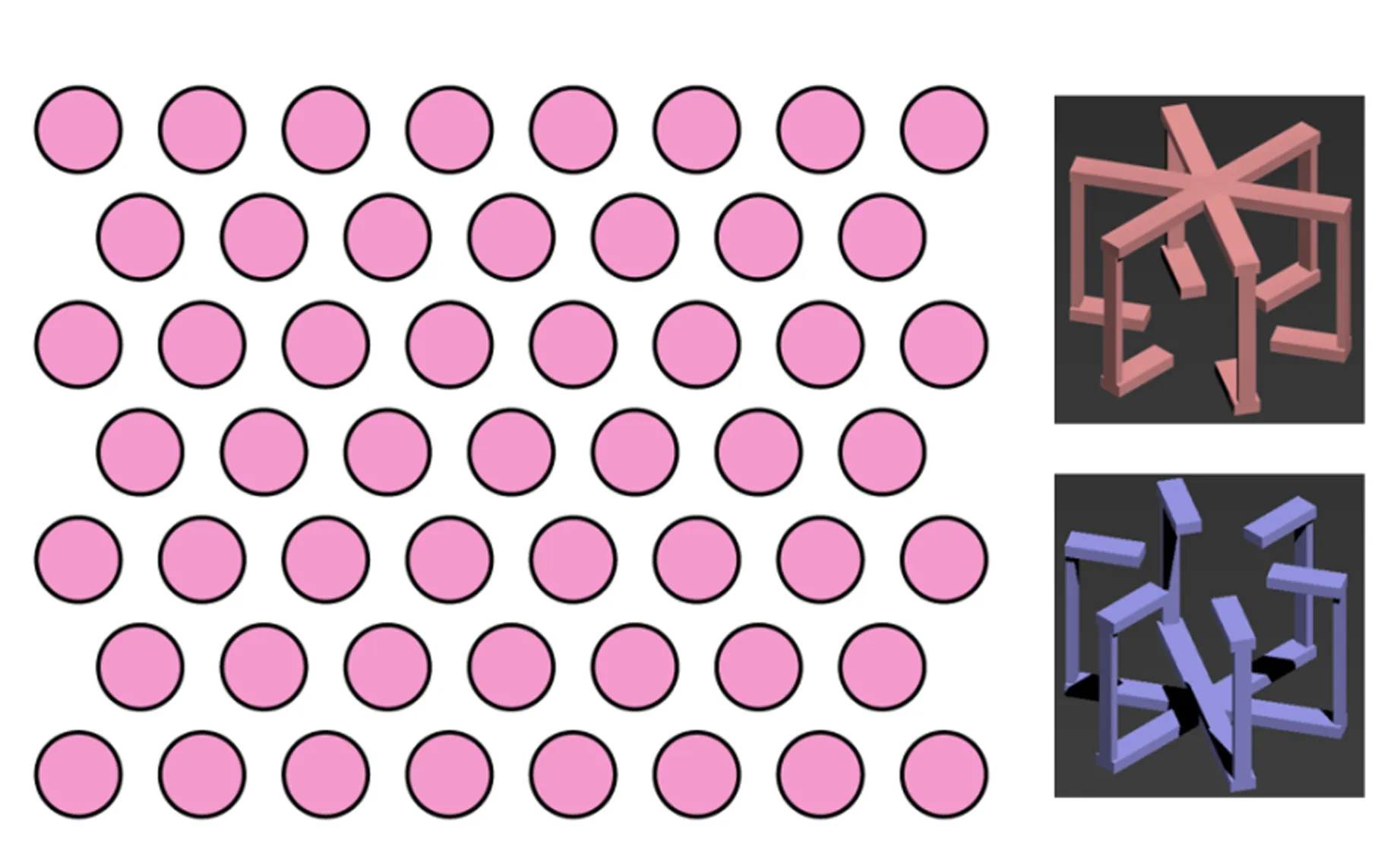
图5 二维三角格子电磁对偶光子晶体

(a)赝自旋向上 (b)赝自旋向下图6 电磁对偶光子晶体中的单向传输赝自旋态
自旋陈数非零的电磁对偶光子晶体虽然从理论上克服时间反演对称性破缺的难题,但是自然界材料一方面难以满足电磁对偶条件,另一方面双各向异性系数十分小(基本等于0). 因此,拓扑非平庸的电磁对偶光子晶体难以实现. 2014年,中山大学研究组克服该实验难题,观察到了赝自旋单向光传输和抗散射传输行为[21]. 电磁对偶条件可以通过超构材料等人工结构来实现. 如图7所示,调整陀螺型序构材料(青色框标记)和米字型超构材料(灰色框标记)的结构参数,可以在宽频段范围内满足电磁对偶条件. 针对非零双各向异性系数,在以上电磁对偶超构材料的上下面引入金属平板. 理论公式推导发现金属平板波导中横电和横磁波导模式发生耦合,从而实现等效双各向异性系数. 由于该等效双各向异性系数由波导模式阶数、模式频率和波导高度决定,所以通过调整结构参量(例如减小波导高度)可以获得大的等效双各向异性系数. 微波实验中,研究者设计不同的超构材料分别实现了拓扑非平庸和拓扑平庸的电磁对偶光子晶体,并用这2种拓扑不同的电磁对偶光子晶体形成边界,观察到与图6相似的单向传输赝自旋态,证实了边界态具有赝自旋过滤效应. 同时引入缺陷,通过完整波导和缺陷波导透射谱线测量,证实了边界态的抗散射传输性质.

图7 电磁对偶光子晶体
4 能谷光子晶体与片上硅基光波导
电磁对偶光子晶体虽然能够实现时间反演对称系统中的非平庸拓扑相,但是由于其较为苛刻的材料参量需求,无法推广到片上硅基等微纳体系,无法真正实现光通讯频段乃至光频段的抗散射传输行为,这亟需找到结构简单、材料参数要求不苛刻的拓扑光子晶体. 2017年,中山大学研究组基于前期研究基础,通过引入能谷自由度,实现了能谷光子晶体,为新型片上硅基光波导提供了新的设计方案[25-29].
图8所示为二维全电介质能谷光子晶体,其原胞如图8上方菱形虚框内结构所示,由2个介质圆柱(圆柱A和圆柱B)和背景空气组成[26]. 光子晶体的晶格常数量a,2个介质圆柱的相对介电常量取为11.7. 当2个圆柱的直径相等时,即dA=dB=0.44a时,横磁模式的2条最低能带如图8中灰色曲线所示,在布里渊区角落K′和K上出现了线性能带,即狄拉克锥. 需要指出的是该狄拉克锥由蜂窝状光子晶体的空间反演对称性和时间反演对称性共同保护形成. 当其中1种对称性破缺时,狄拉克锥会被打开. 为了获得结构简单的拓扑光子晶体,采用能谷光子晶体研究空间反演对称性破缺的情况. 为了破坏光子晶体的空间反演对称性,可以调整2个圆柱的直径. 当圆柱A和圆柱B的直径不相同时,空间反演对称性破缺,波矢K′(或者K)点的对称性从原来的C3v降为C3. 原本简并的2个模式发生模式劈裂,且波矢K′和波矢K上所得本征模式具有不同的涡旋相位. 这种涡旋相位的区别表明位于不同波矢的模式性质不同. 由于在波矢K′和K附近能带呈现“山谷”形状,具有能量极值,因此用能谷自由度来标记倒格矢空间中能量极值,并区分波矢K′和K附近不同的能带.
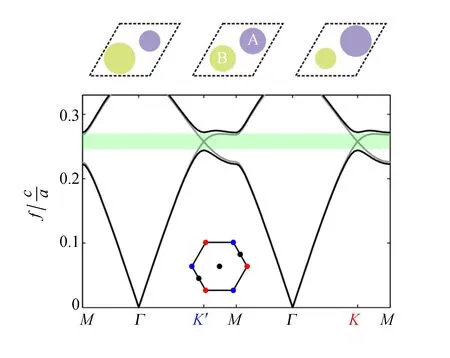
图8 二维能谷光子晶体结构及其横磁模式能带
如图8所示,伴随着模式的劈裂,全向光子禁带随之出现(绿色框). 研究表明,该禁带由另一个拓扑不变量(能谷陈数)表征. 图8上方左右侧的2个光子晶体中圆柱的结构参量分别为dA=0.19a,dB=0.25a(左,记为能谷光子晶体1)和dA=0.25a,dB=0.19a(右,记为能谷光子晶体2),它们的能谷陈数分别是1和-1. 2个拓扑属性不同的光子晶体边界上存在拓扑依赖边界态. 用能谷陈数不同的能谷光子晶体构建边界,同样可以得到拓扑依赖的边界态. 为了说明这一结论,以锯齿状形貌的光子晶体边界为例(图9). 边界下方和上方分别是能谷光子晶体1和能谷光子晶体2,2个能谷光子晶体的交界处形成边界.
数值模拟仿真结果表明,在K′能谷处有1条正群速度的边界态,而在K能谷处有一条负群速度的边界态. 图9(b)方给出了该边界态电场振幅的分布图. 可以发现,边界态能量集中在中心的边界区域,远离中心边界能量逐渐减小,与边界态的定义相符合. 当2个能谷边界态之间的耦合被抑制时,可以实现光的高透传输. 文献[30]表明,对于锯齿状边界或者转弯波导,能谷边界态的相互解耦合、能谷边界态之间的耦合被抑制,因此基于能谷光子晶体的波导有望实现光的高透传输. 为了说明这一现象,研究由图9边界形成的Z型转弯波导(图10). 在转弯波导的左上方设置输入源,在转弯波导的右下方测量透射率. 于此同时,计算直波导的透射率作为参照. 当激发的边界态传输并遇到转角时,可能散射方式有2种,一种是散射到能谷光子晶体体态中,另一种是散射到后向传输的边界态. 当激发频率落在能谷光子晶体的全向禁带频率时,所激发的边界态散射到光子晶体体态的通道被阻断. 与此同时,由于Z型波导满足能谷边界态解耦合条件,因此相邻能谷边界态之间的散射通道也被阻断. 至此,所有的散射通道都被阻断,激发的电磁波遇到Z型波导转角时,只能继续向前传播,最终实现了抗散射传输. 图10展示了边界态在Z型波导中传输时电场强度分布情况,可以看到电场强度在传输过程中没有发生震荡,电磁波很好地绕开边角向前传输,实现了抗散射传输. 同时,Z型转弯波导的透射率与直波导的透射率相同. 模拟结果表明能谷光子晶体波导支持抗散射传输边界态.

(a)结构

(b)模式图9 能谷光子晶体形成的边界及其支持的边界态

图10 能谷光子晶体的抗散射传输边界态
能谷光子晶体结构简单,对材料参量的要求不苛刻,可以推广到片上硅基系统[28,31]. 如图11所示,在蜂窝状光子晶体中引入反结构,即原胞由2个空气圆柱嵌套在高折射率的硅材料中[28]. 由于采用了反结构,而且硅平板在z方向上为有限高度,因此硅基能谷光子晶体考虑的模式是类横电模式. 虽然结构与模式偏振发生改变,但是受结构对称保护的线性狄拉克锥能带仍然会出现在布里渊区边界上. 与图8中的能谷光子晶体相似,当2个空气圆柱的直径不同时,空间反演对称性被打破. 同样地,原本简并的狄拉克锥能带会打开并形成禁带,而禁带上下的体能带的能谷陈数非零. 2个能谷陈数不同的硅基能谷光子晶体平板可以形成如图11(a)的直线波导. 该直线波导的边界态色散曲线如图12所示(红色曲线). 边界态存在于线性光锥以下,也位于光子晶体平板的方向禁带中,所以边界态传输时既不能耦合到空气,也不能散射到光子晶体平板内部.
当2个能谷处的边界态不能相互耦合时,该边界态具有抗散射传输性质. 为了证明边界态的抗散射传输性质,实验中还制备了Z型和Ω型波导[见图11(b)和(c)].

(a)直线型

(b)Z型

(c)Ω型图11 硅基能谷光子晶体平板组成的直线、Z型和Ω型波导

图12 硅基能谷光子晶体平板的直线波导的边界态色散

图13 硅基能谷光子晶体组成的直线、Z型和Ω型波导的透射谱线测量
实验中测量了3种波导的透射率,直线、Z型和Ω型波导的透射谱线分别见图13中蓝色、绿色和红色曲线. 可以发现,当波长位于1 515 nm至1 640 nm区间时,透射率较高,这与该波长范围内存在光锥下边界态直接相关. 同时,3个透射率基本相等,这说明转弯波导中的多个240°转弯角并不会引起2个能谷处边界态的耦合. 基于能谷光子晶体的片上硅基光波导,具有特征尺寸较小、传输损耗较小、工作带宽较大的优点. 目前,该片上硅基光波导的设计实验方案已被多个研究小组采用,进行微腔设计、激射、分束器等应用研究[32-33].
5 结束语
从1987年S. John和E. Yablonovitch共同提出光子晶体概念,到2008年F.D.M. Haldane等将拓扑原理引入光子晶体研究,光子晶体研究经历了理论研究、实验验证、应用探索等阶段. 目前,因具有结构可灵活调整、工作频段宽、性能稳定等优点,拓扑光子晶体已经成为基础光物理探索和前沿光子学应用的重要研究体系之一. 本文介绍了几种具有代表性的二维拓扑光子晶体,从发展历程角度介绍了几种拓扑光子晶体的理论原理和实验方案,并介绍具有单向传输和抗散射传输性质的边界态,以及新型光波导的结构设计和性能表征. 限于篇幅,关于其他类型二维拓扑光子晶体、一维和三维拓扑光子晶体的研究可以参考近期拓扑光子学综述或者前沿科学论文[34-40]. 当前,拓扑光子晶体的理论体系已趋于成熟,下一步研究工作在于探索拓扑光子学与传统微纳光子学的深度融合,将丰富的拓扑物理应用于实际的光学应用中,为性能稳定的片上光子器件乃至级联光学系统提供设计新方案. 此外,本科实验教学也越来越重视教学内容的前沿性. 目前,中山大学物理实验中心已将部分光子晶体研究内容转换为物理学专业实验内容,通过前沿科学知识与本科实验内容的结合,让学生在本科阶段接触并了解到科学研究的最新进展.

