旋转流场流态预测模型验证及其速度分量选择的差异性

王衍，曹志康，王英尧，胡琼，胡鹏，肖业祥

（1江苏海洋大学机械工程学院，江苏连云港222005；2清华大学水沙科学与水利水电工程国家重点实验室&能源与动力工程系，北京100084）

叶轮机械广泛应用于国民生产的各个环节，是动力工程行业最关键、最重要的部件之一。对叶轮机械的研究避免不了要对叶轮内部的流体流动形式和状态进行判断。依据流体力学基本原理及经典润滑理论，流体运动主要包括4种形式：①管中流动和缝隙流动；②（固体外部的）绕流；③（固体一侧的）明渠流动；④孔口出流和射流。就叶轮机械设备而言，多属于第一类和第二类流动形式，也可以将压缩机、泵、离心机等叶轮旋转类机械类比为疏导流体的一种异形管道。

目前，雷诺数模型被广泛用于流体在管流时的流态判定，已被实验完美验证，属于经典流体力学基础理论。对于缝隙流动，相关学者[1]提出了流动因子判定模型，即同时考虑压差流和剪切流进行流场流态计算，结论得到许多学者认可并被广泛采用，近期的研究结果也表明流动因子模型对于缝隙流的流态判断符合预期[2-5]。而对于叶轮类机械而言，一方面存在管流特点，部分还具有缝隙流特性，甚至多数场合还包含有高速的旋转绕流，流场情况异常复杂。单纯依靠经典雷诺数模型或流动因子模型对此类旋转流场进行流态判断受到了诸多学者的质疑[6-7]。以干气密封或上游泵送机械密封等微尺度有槽旋转流场为例，针对流场的流态划分问题存在较大争论[8-10]，部分学者[11-14]在计算时选择基于层流流态进行分析计算，而部分学者[15-16]鉴于微尺度旋转流场的复杂性和不确定性，选择低雷诺数的湍流模型进行计算求解。

可见，建立一个相对合理、准确的旋转流场流态的判定模型或方法是正确、科学研究叶轮类旋转流场的必要理论基础，也是旋转机械特性计算中亟需解决的一个基础性科学问题。鉴于此，本文基于对干气密封（dry gas seal,DGS）和上游泵送机械密封（upstream pumping mechanical seal,UPS）等微尺度有槽旋转流场宏观特性系统分析的基础上，对提出的椭球模型及其速度分量选择作进一步深入分析和讨论。

1 基础理论

1.1 雷诺数

雷诺数（Re）是流体力学中表征黏性影响的相似准则数，1883年由英国人雷诺（Reynolds O）根据流体在管道中的流动规律提出。依据雷诺数的大小可以对流体流态进行判定，表达式见式(1)。

式中，υ为运动黏度，m2/s。可以看出，流体流态与流速V(m/s)、管径d(m)、动力黏度μ(Pa·s)和密度ρ(kg/m³)有关。

图1所示为管流中的雷诺数模型流态判定准则：当雷诺数Re≤2300时表示流态为层流，2300＜Re≤4000时为过渡流动状态，Re＞4000时为完全湍流状态。

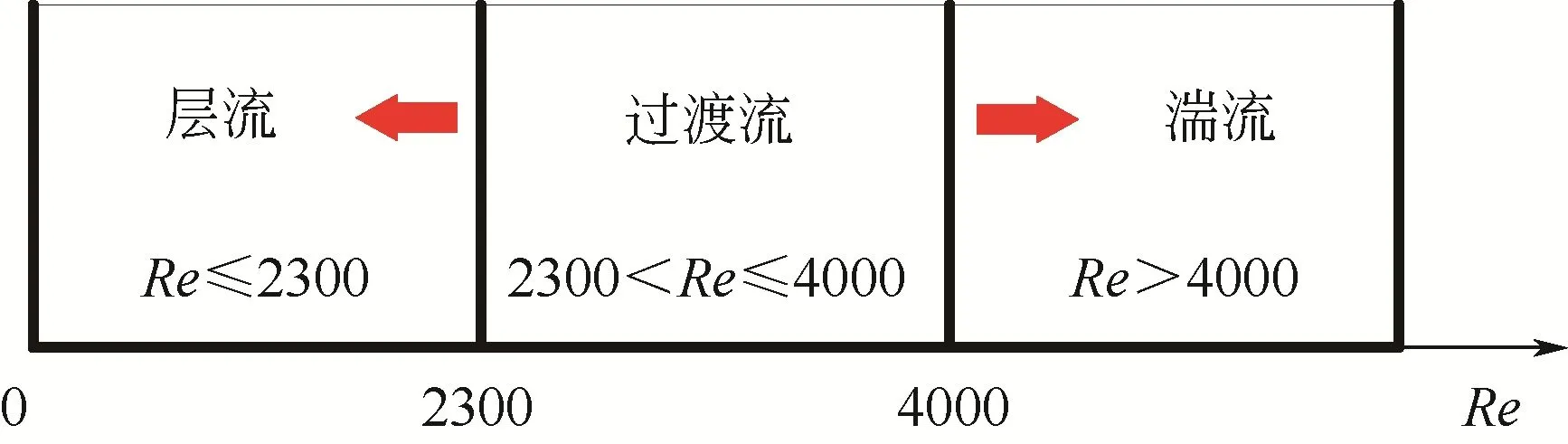
图1 管流雷诺数判定模型

1.2 水力直径

雷诺数的量纲为1，通式可以表示为Re=VdH/υ，其中dH为特征尺寸（m）。在管流中，特征尺寸即为圆管直径d，在其他异形管道中，特征尺寸dH可由式(2)确定。

式中，A为流过管道端面的断面面积，m2；S为断面上流体与固体的接触边界周长，m。

1.3 缝隙流动及判定模型

机械设备中常见的缝隙流动形式主要有平面缝隙、环形缝隙及平行圆盘缝隙。为简化分析，环形缝隙及平行圆盘缝隙通过平面展开以后也可以看成平行板间的流动问题，如图2所示，其中Vy为平板缝隙间流体在y方向的流动速度（m/s）；h为平板缝隙间距（m）；l为平板缝隙长度（m）。当缝隙尺寸很小、流体黏度很大时，此时的缝隙流动可看作是层流，解法与管流类似，可直接采用雷诺数模型进行判定。但是当缝隙尺寸微观且流体黏度较小时，需要依据缝隙流区别于管流的特性进行分析判断。

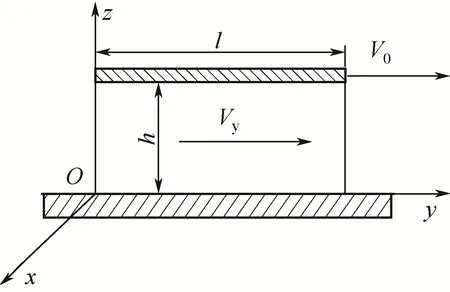
图2 平板缝隙流动

平板缝隙中的流体流动有两种形式：一种为压差流，也称为哈根-泊肃叶（Hagen-Poisedille）流；一种为剪切流，也作库埃特（Couette）流。压差流和剪切流可以同时存在于缝隙流场中，如机械密封、液压泵、液压马达等，有时两种流动又可以单独存在，如高速轻载时的同心滑动轴承内就只存在纯剪切流，固定柱塞缝隙、静压支承等只存在纯压差流。基于此，Brunetiere等[1]提出了同时考虑压差流和剪切流的流动因子ξ模型，在流场中存在多种流动时可利用这一模型进行准确地判定，见式(3)。

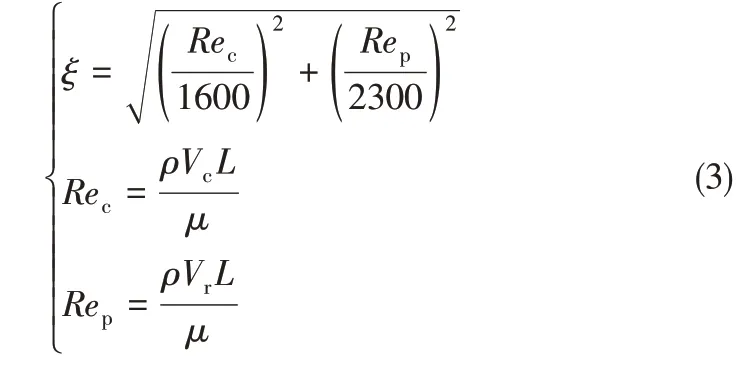
式中，Rec和Rep分别为单独考虑Couette周向剪切流和Poiseuille径向压差流的雷诺数。对应式(3)可用两等偏心率的椭圆模型表示，如图3所示。类似于管道雷诺数判定模型，规定ξ＜9/16时表示流体处于层流状态，9/16≤ξ≤1时为过渡流动状态，ξ＞1时为完全湍流状态。目前，流动因子模型[17]已被证实是可靠和科学的。

图3 流动因子判定模型

2 旋转流场流态模型的提出

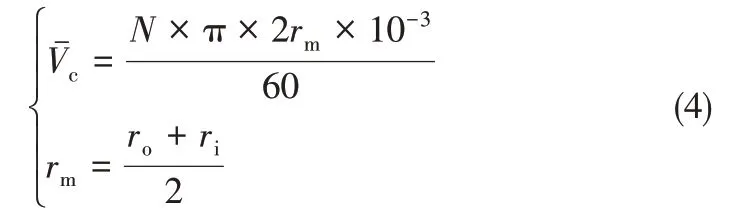
式中，ro为动环内径，m；ri为动环外径，m。

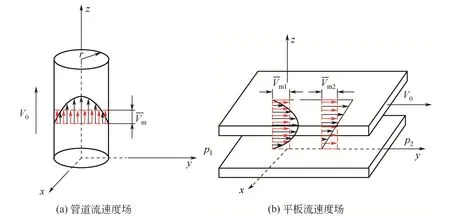
图4 管流和平板流的速度场分析

图5 典型旋转流的速度场

工程计算中，鉴于间隙流动中出现了旋转流，多数学者认为此时的流场不稳定，极易受外部影响而出现紊流情况，多考虑选用湍流模型进行求解计算，如推力轴承、水轮机、风机等。轴向绕流结构（叶片、深槽等）不显著时，为简化分析，也常作层流假设，如机械密封、干气密封、上游泵送机械密封等，后面两种密封形式的旋转面开有微尺度槽深结构。

经典理论已证明管流中出现湍流的原因[18-20]：原有层流流动中出现了垂直于轴向的速度分量。相关学者[21-24]在研究气浮类支承出现自激振动的过程中也指出，自激振动和气旋现象的发生与流场中出现垂直于原流场方向的流动密切相关。另一方面，当旋转流场中存在扰流结构时（如螺旋桨叶片、密封槽、推力轴承片等），在高速时对流场的影响显著，极易形成沿轴向的速度分量（Va，m/s），如图6所示。

本文作者课题组[25-26]近期针对干气密封微尺度旋转流场的研究结果也表明：旋转流场中同时存在周向、径向和轴向速度分量，轴向速度的影响在低速时可以忽略不计，但在高速时应予以考虑。基于此，在一维雷诺数模型和流动因子模型的基础上，提出了同时考虑周向、径向及轴向速度分量的三维椭球模型，见式(5)～式(7)。

图6 高速波动时旋转流的速度场

式中，ρ为流体的密度，kg/m3；V为速度分量，m/s；dH为特征尺寸，m；下角标c、p、a分别表示周向、径向及轴向这3个方向。

如式(5)所示，相比于流动因子判定模型，椭球模型不仅包含有单独考虑Couette周向剪切流和Poiseuille径向压力流时的雷诺数Rec和Rep，还考虑了轴向速度分量对应的雷诺数Rea的影响。算式(6)和(7)分别为三类雷诺数对应的计算模型及水力直径计算模型，图7(a)～(c)分别为周向、径向和轴向速度分量对应的水力直径物理模型，其中，B为密封环宽度（mm）；rm为计算区域平均半径（mm）。

图7 水力直径计算模型

分析三维椭球判定模型可知，式(5)对应的判定模型为一空间等偏心率椭球体，如图8所示，其对应的判定方式可表述为：当λ＜9/16时对应的流态为层流，λ＞1对应的流态为湍流，9/16≤λ≤1表示处于层流到湍流的过渡区，此时的流场开始出现扰动因素。

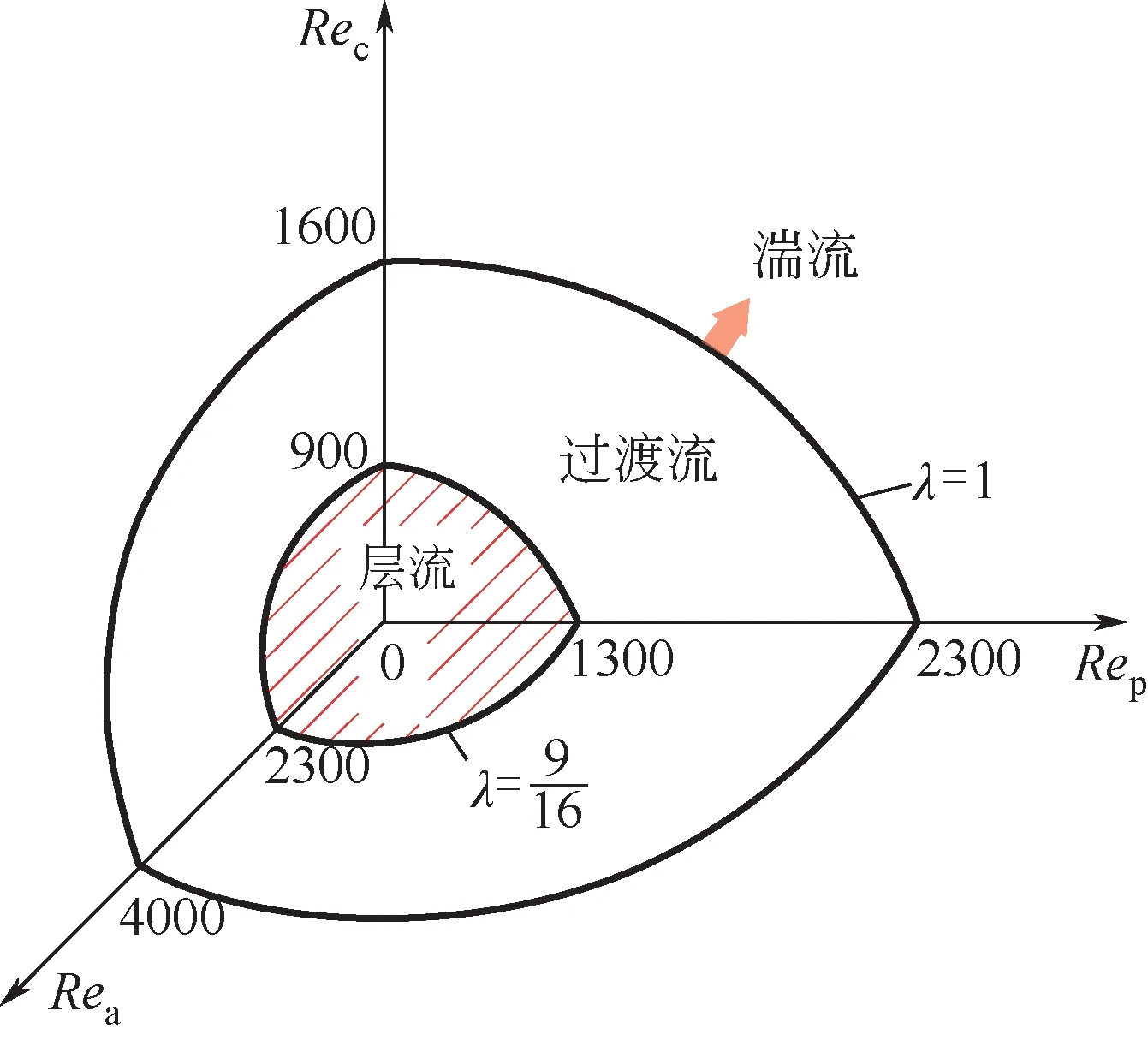
图8 椭球判定模型

3 速度分量选择的差异性

3.1 计算方法

本文假定流体为连续介质，计算分析选用Fluent三维流动求解器对流体流动进行数值模拟，控制方程如下。

N-S方程见式(8)。

式中，ρ为流体的密度，kg/m3；V为密封间隙气体总速度，m/s；F为气膜推力，N；∇为梯度；p为密封间隙压力，N；μ为气体介质动力黏度，Pa·s。

连续性方程见式(9)。

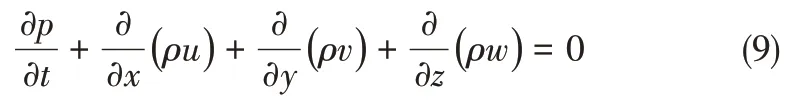
对N-S方程组的直接求解称为DNS（direct numerical simulation）法，只要满足连续介质假设，DNS方法并不需要对层流或湍流进行额外建模，但DNS计算量大、效率低，实际应用较少。Fluent求解器中的Laminar模型即为对满足连续性介质假设的N-S方程的直接求解，只是网格尺寸、时间步长及计算效率相对较低，但仍具有较好的精度。鉴于此，本文计算采用Laminar模型，压力与速度的耦合采用SIMPLEC算法，亚松弛迭代求解。

3.2 速度分量选择

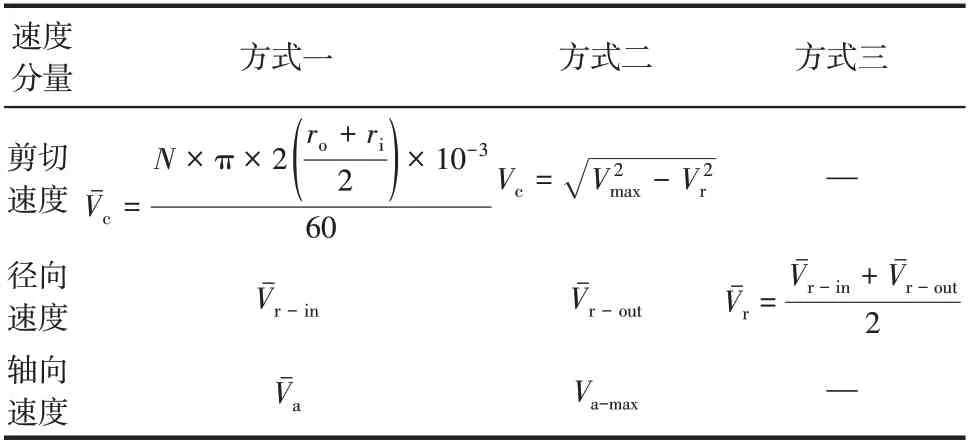
表1 三类速度分量的选择方式

3.3 速度分量的差异性分析

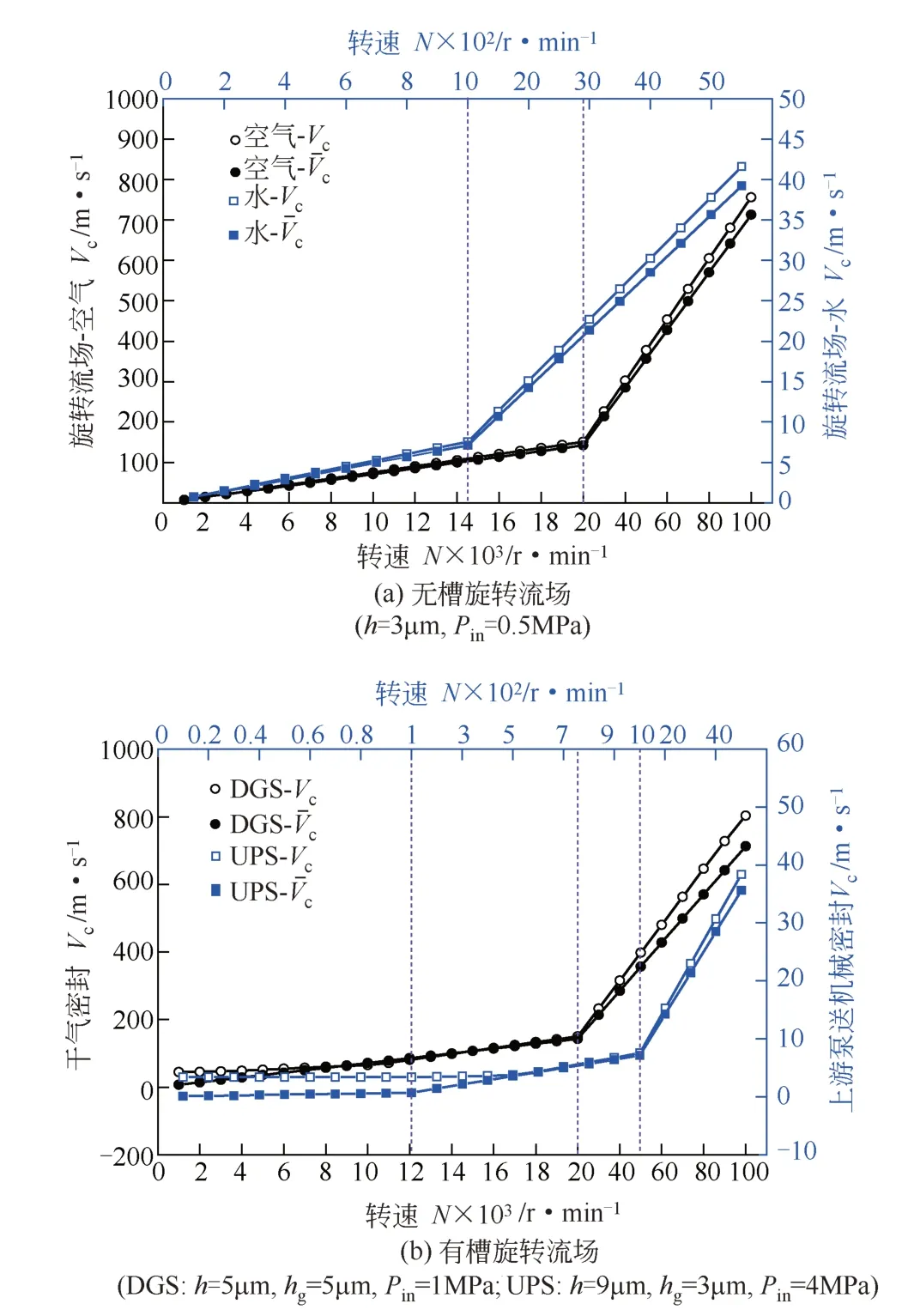
图9 两类旋转流场中剪切速度的差异性

图9(a)和(b)所示分别为不同介质在无槽旋转流场及有槽旋转流场（DGS和UPS）中两种剪切速度下随转速变化的趋势，可见，通过平均直径直接计算的剪切平均速度与通过公式计算的剪切速度差异性不大，二者随转速的升高都呈线性增加趋势，差异性也略有增大。整体而言，两种剪切速度的计算结果非常接近。

图10所示分别为无槽旋转流场中不同密封介质（水和空气）及有槽旋转流场（DGS和UPS）中不同径向速度随转速的变化趋势，由图可见，干气密封和上游泵送出、入口的径向速度略有不同，这是由密封内外径压差、流体间的黏性力等因素造成的。其中，干气密封的径向速度随转速增大呈增大趋势，当转速达到一定值时，径向速度的增加幅度降低甚至出现下降趋势；不同介质下的无槽旋转流场及上游泵送的径向速度随转速增大呈缓慢下降趋势，转速越高下降趋势越明显，原因可能是流场在较低转速时存在少部分紊流区域，随着转速的升高，流场流态逐渐发生了完全转变。进一步分析还可以看出，不同转速下两个面上的径向速度分量差值基本保持不变。

3.3.3 轴向速度Va的差异性分析

图11分别为无槽旋转流场及有槽旋转流场（DGS和UPS）中最大轴向速度和平均轴向速度随转速变化的趋势。由图可见，最大轴向速度和平均轴向速度的差距很大，不同转速下的平均轴向速度近趋于零，可忽略不计，最大轴向速度则随转速增大呈缓慢增大趋势，与转速关联较大。最大轴向速度为正值，而平均转速近趋于零，对流场分析发现，这是由于流场中大部分区域的轴向速度分量非常小、近趋于零且部分区域还存在相反的速度值（负值），只在少部分区域出现正向轴向速度，使得平均后的轴向速度趋于零，鉴于此，下文将结合模型的验证及宏观密封特性分析，对轴向速度的差异性作进一步研究。

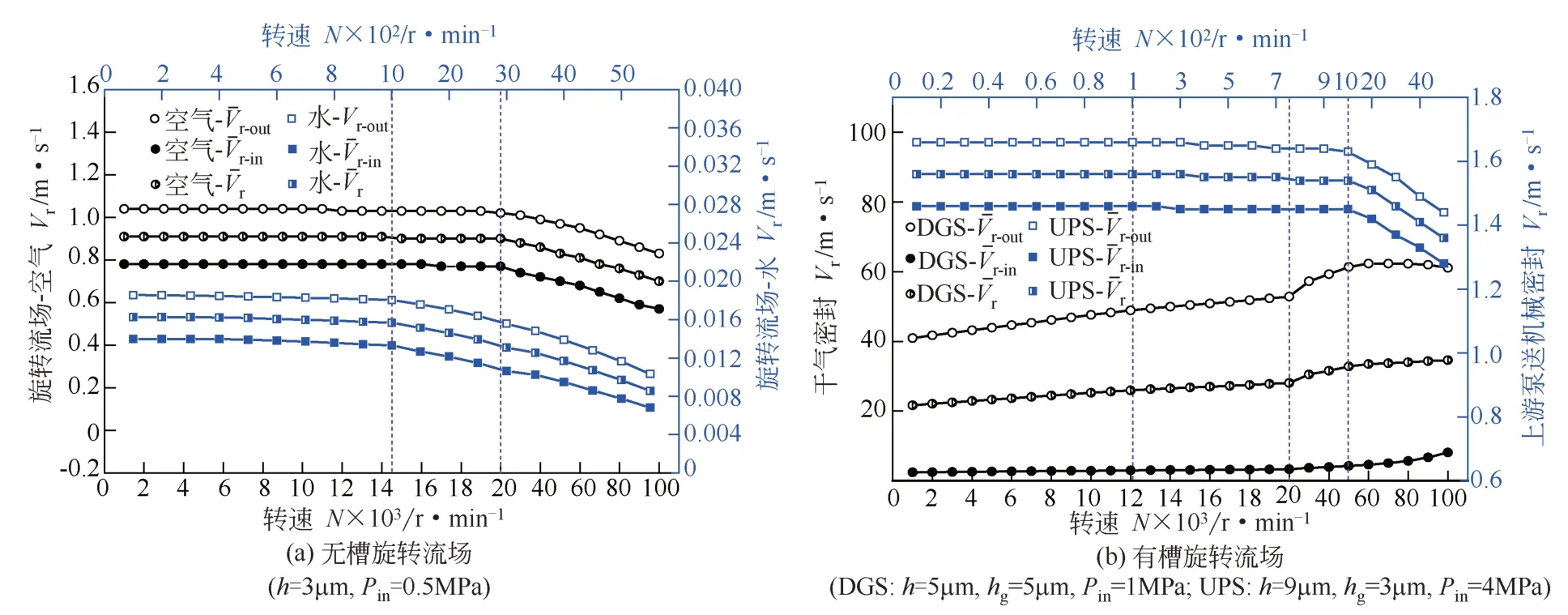
图10 两类旋转流场中径向速度的差异性

图11 轴向速度Va的差异性

综上可见，两种剪切速度的差异性不大，为简化计算，可直接选择方式一中平均直径处的线速度为剪切平均速度；入口面和出口面的径向速度差值恒定，可选择方式三中的计算方法；轴向速度均值过小，最大值与转速关联较大，初步考虑选择最大轴向速度进行分析计算，下文将结合模型的验证及宏观密封特性分析对不同转速的差异性作进一步研究。

4 三类模型的验证与分析

4.1 管流中模型的验证

为验证椭球模型的正确性，选择经典雷诺数模型为标准，进行椭球模型的验证。因为流动因子模型是面向缝隙流的，这里不作考虑。为使验证结果具有代表性，流体选择水和空气两种介质分别验证。模型选择及相关参数如表2所示。

依据模型中速度选择特点，轴向、径向及周向速度皆选择平均速度代入计算。表3和表4分别是介质为水和空气时两种模型的判定结果，由表3可知，管流中的速度分量大小以轴向速度分量Vˉa为主，其他两种类型的速度分量值很小，椭球模型的判定结论与经典雷诺数的判定结果对应的十分理想。如表3和表4所示，层流时雷诺数（Rea＜2300）对应椭球模型的层流范围（λ＜9/16=0.56）；过渡阶段雷诺数（2300≤Rea≤4000）对应椭球模型的过渡阶段（0.56≤λ≤1）；完全湍流时雷诺数模型（Rea＞4000）对应椭球模型的完全湍流范围（λ＞1）。对比结果的一致性说明椭球模型在管流中具有一样的判定精度，一样适用于管流中的流态判定。

表2 管流模型验证的相关参数

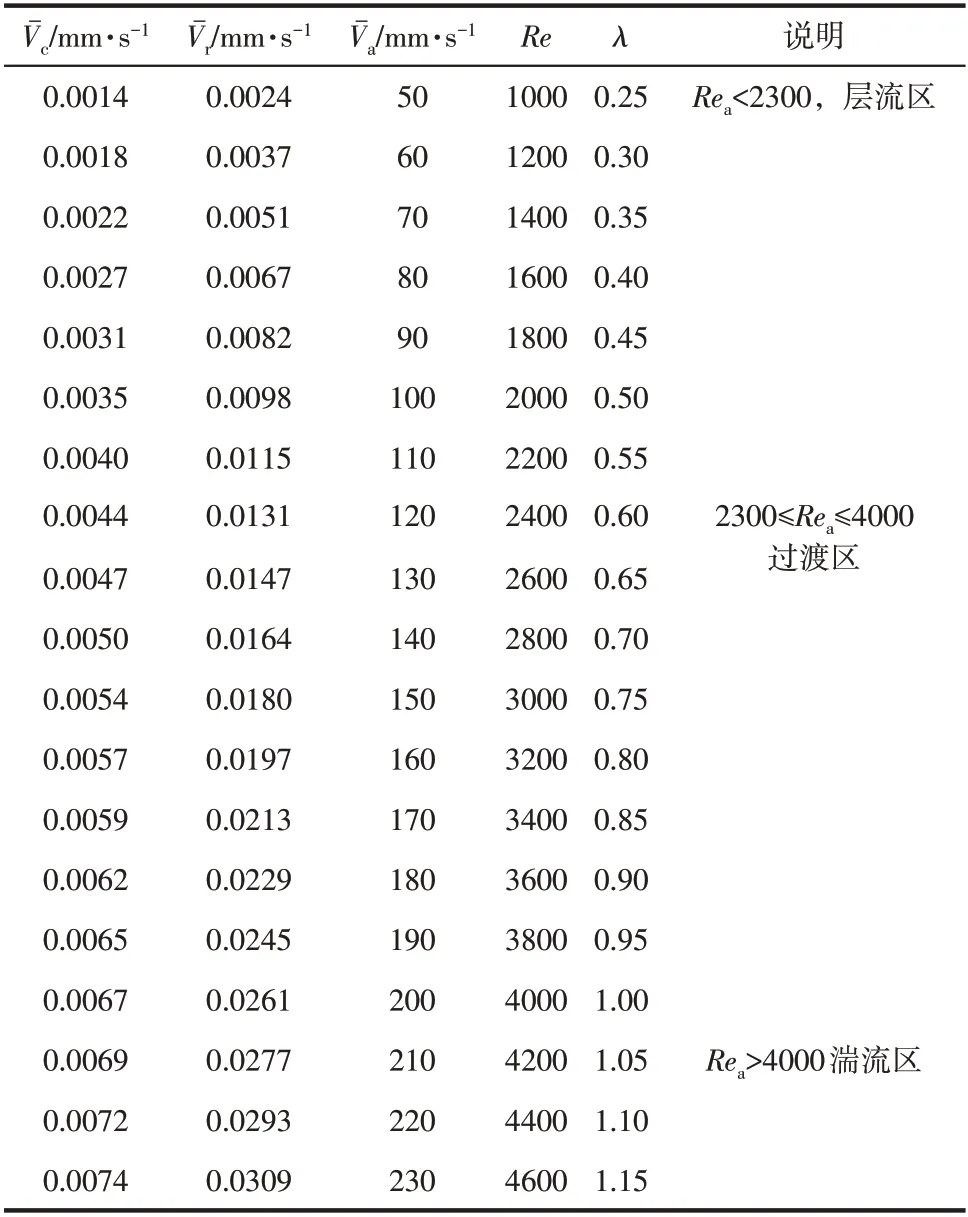
表3 管流中三类模型判定值对比（水）

表4 管流中三类模型判定值对比（空气）

4.2 无槽旋转流中模型的验证

类似于管流模型中的验证方式，以接触式机械密封的无槽旋转流场为模型基础，验证三类模型在旋转流场中的判定结果。选择水和空气为介质进行流场计算，模型选择及相关参数如表5所示，1号环和2号环分别为动环和静环。

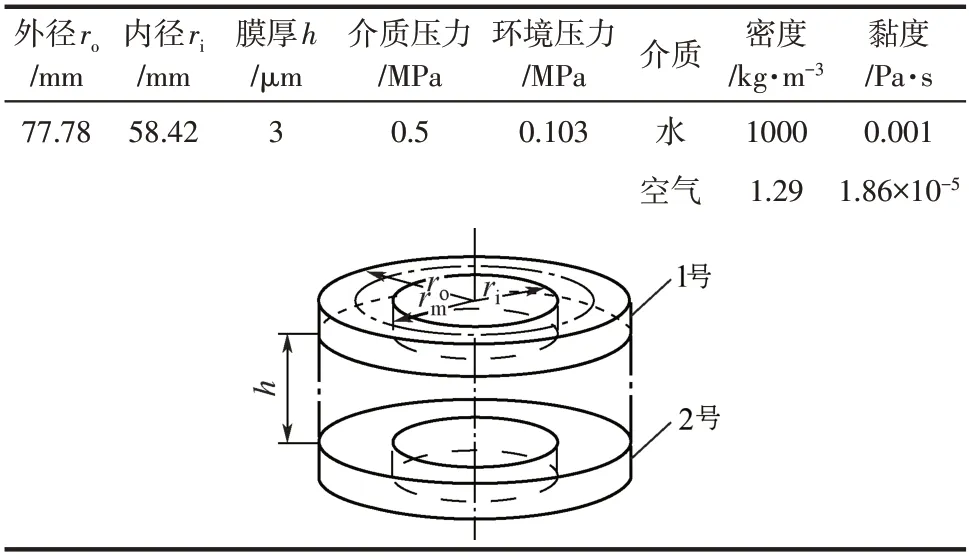
表5 旋转流模型验证相关参数

图12为不同转速下的旋转流场中三类模型的判定值变化趋势，实际计算的转速范围为0～2×105r/min，鉴于转速变化区间较大且需进一步对转速进行拟合，转速变化采用非等比例方式标定。由判定值的变化趋势可以看出，3种模型的判定值与转速基本呈线性变化关系，基于此，同时依据三类模型的判定临界值，拟合得出了相应的临界转速，如对应表格所示。

由图12及其中对应的表格可以看出，旋转流场中3种模型在不同流态下对应的临界转速都不同，差别较大，不同介质下的椭球模型、流动因子模型和雷诺数模型对应的临界转速依次升高，雷诺数模型的临界转速值最大，介质为空气时的完全湍流临界转速甚至达到了1.34×106r/min。3种模型临界转速不同的直接原因是对应数学模型的差异，雷诺数模型仅考虑了压差流造成的轴向速度分量，流动因子模型在此基础上考虑了剪切流造成的周向速度分量，而椭球模型进一步考虑了垂直于主流速度场的速度分量。

4.3 有槽旋转流中模型的验证

综合管流及无槽旋转流场的对比结果可以看出，椭球模型在管流中与经典雷诺数模型具有良好的一致性，在旋转流场中的临界转速最低。从椭球模型的判定方法中可以看出，其考虑的速度分量更加全面，为进一步说明其判定的科学性和准确性，面向上游泵送机械密封及干气密封两种典型有槽旋转流场，系统研究此类高转速、扰流强的旋转流场特性及模型判定精度，同时对速度选择的差异性进行讨论。

4.3.1 上游泵送机械密封旋转流场分析

表6所示为上游泵送机械密封的仿真计算参数，计算结果如图13所示。可以看出，转速越高，三类模型的判定值误差率越大，与无槽旋转流场类似，依据雷诺数模型、流动因子模型得到的湍流临界值依次降低。不同的是，从低转速开始，依据椭球模型的判定结果（λ＞1），表明上游泵送旋转流场中的流体流态应为湍流。

4.3.2 干气密封旋转流场分析

选择诸多文献中的经典参数为干气密封的计算参数，如表7所示，计算结果如图14所示。类似于无槽旋转流场和上游泵送旋转流场，三类模型对临界值的判定结果差距较大，椭球模型对应的临界转速值最低。依据椭球模型的判定结果，在本文计算工况下，干气密封微尺度流场中层流至过渡流的临界转速为5000r/min，过渡流至湍流的临界转速为9000r/min。

表6 上游泵送机械密封相关参数

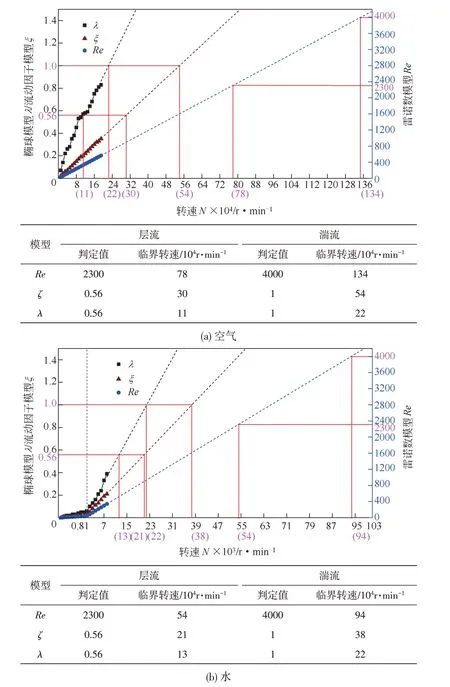
图12 旋转流场

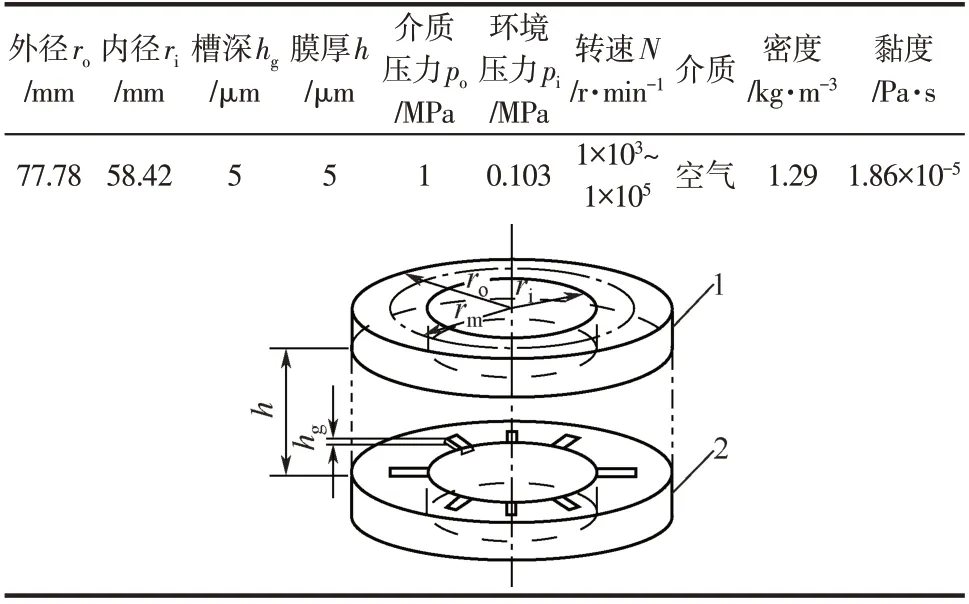
表7 干气密封相关参数

4.4 有槽旋转流场宏观特性分析

图13 上游泵送机械密封

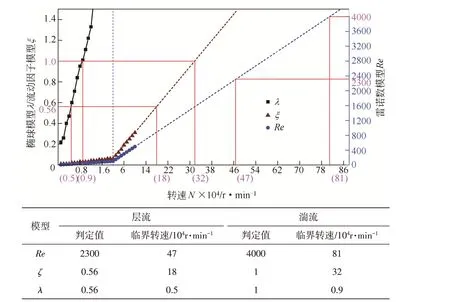
图14 干气密封

本文作者课题组[27]近期研究表明，超高速时干气密封流场会出现扰流现象，即动压效应不随转速升高而持续增大，这与相关文献[28-29]中普遍存在的中低速下开启力、泄漏量随转速升高而增大的结论有所不同，造成这一变化的原因可能是随着各参数的变化，微尺度下的流体流动出现了波动现象，即流场流态发生了改变，宏观表现则为泄漏量或开启力出现了变化拐点。基于此，对上游泵送机械密封的宏观特性也作了类似分析，如图15所示。

图15(a)所示为干气密封的开启力和泄漏量随转速的变化规律，可以看出，此时开启力和泄漏量都出现了拐点现象，就拐点对应的转速值而言，泄漏量要早于开启力，分别为50000r/min和70000r/min。图15(b)所示为上游泵送机械密封的开启力和泄漏量随转速的变化规律，此时开启力的拐点也很明显，约在转速为70000r/min，而泄漏量的变化略显复杂：泄漏量在一定转速范围内（＜10000r/min）基本维持正泄漏量不变，说明此阶段未实现上游泵送，随着转速的持续增大，泄漏量迅速下降，突破零泄漏点后进一步实现了显著的上游泵送功能。这一特性是由上游泵送的结构特点决定的，即动压槽开于密封环内径处的原因，转速越高，泵送效应越显著，所以不会出现类似干气密封式的泄漏量拐点现象，拐点现象可通过开启力规律特性分析。

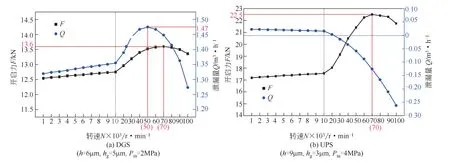
图15 不同密封形式的宏观特性变化

上述临界转速的出现只是相关性能参数的宏观拐点表现，实际流态改变时的临界转速应该更早，即对应流态改变的转速值应低于拐点对应的转速值。基于此，表8所示为对应图15工况下三种模型的判定结果，可以看出，椭球模型符合上述临界转速预期范围，其判定结果与旋转流场的实际更相符，原因可能是椭球模型较其他模型考虑的速度分量更加全面，在高工况下的判定结果较其他模型更加准确；特别是引入最大轴向速度分量，与宏观特性关联紧密，可以更好地反应实际流场流态的变化。由此，可对三类模型的适用性作初步讨论：雷诺数模型适用于管流流体流态的判定，流动因子模型适用于无槽低速旋转流场的判定，椭球模型考虑因素最多，适用于管流流体流态判定的同时，对旋转流场特别是高速旋转流场的判定效果更贴近实际。

表8 对应工况下的模型判定结果

5 结论

（1）旋转流中出现了垂直于旋转流动的速度分量（轴向速度分量），是形成旋转流不稳定流动的主要因素，对旋转流场的判断需考虑轴向速度分量的因素。

（2）基于周向、径向和轴向速度分量建立的三维椭球模型与经典雷诺数模型在管流时符合较好，在高速旋转流时，椭球模型具有更高的判定精度，与实际情况更加符合。

（3）利用椭球模型进行旋转流场流态的判定，轴向速度分量选择流场中的最大值进行计算，得出的临界转速更加接近宏观流场拐点的临界转速值。