在小学数学课堂培养学生数感的教学实践

梁君

【摘要】本文论述在小学数学课堂培养学生数感的教学实践，建议教师采用紧密联系生活，设计适宜的操作任务;立足于实际问题的应用，加强运算的训练;抽象简化数学问题，建立数学模型等具体方式，逐步培养学生的数感。

【关键词】小学数学 数感 实践策略

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2021）45-0129-02

数感是学生数学学科的素养之一，在小学数学教学中培养学生的数感是一项重要的教学任务。《义务教育数学课程标准（2011年版）》将数感的含义阐述为“关于数与数量、数量关系、运算结果估计等方面的感悟”，这表明学生不仅要学习数学知识，还要了解数字之间的关系、数和运算的意义等。数感培养不是简单的认识数字是什么或者学会数数，其形成是一个由浅入深、由具体到抽象的过程，学生需借助大量的运算练习和数学思维训练，在潜移默化中完成对数学知识的建构，进而深刻地理解数字关系、理解抽象和具象之间关系，实现数感培养。本文依据新课程改革的标准，立足课堂，采取结合现实生活、立足实用价值、利用数字建模等方式，探讨在小学数学课堂培养学生数感的策略。

一、联系生活，在操作中建立数感

数学来源于生活，而生活可以提供给学生丰富的感性经验以及感觉体悟。小学生的认知特点和思维特点，决定了其学习比较依赖实际的生活或具体的活动，由此可知，小学生的数感培养也可以联系日常生活。教师要从生活中选取适宜的点设计数学活动，多展示一些生活实例，帮助学生将所学的知识点与生活中熟悉的真实事物相联系，在活动操作中逐渐建立数感，从而能够用数学思维去看待问题、思考问题，从数学角度感受生活。

例如，在教学人教版数学三年级上册《图形的周长》一课时，学生初接触周长的概念，脑海里对“长”的印象比较清晰，对“周长”的印象则比较模糊。课中，笔者初步解释了周长是绕平面图形一周的长度。为了增加学生对周长的实感，笔者展示了三个情境图片，分别是给花坛设计围栏、给窗户镶嵌窗框、给叶子贴上一圈金边做成工艺品，然后让学生思考：应该做多长的围栏？需要多少金属条来制作窗框？需要多长的金边？在情境的启发下，学生提出测量绕花坛、窗玻璃和叶子一圈的长度，即可得知结果，笔者由此明确绕花坛、窗玻璃和叶子一圈的长度（即一周的长度）就是本节课所要学的周长。

理解了周长的概念，那么如何在实际应用中测量周长呢？仍然以上述三个情境为例，花坛围栏和窗户是比较方正的形状，周长相对好测量，但是叶子是不规则的、带有曲线的形状，使用常规的尺子难以得出测量结果，笔者让学生想一想：如果在生活中遇到这种情况，自己会怎么做？学生经过讨论，一致认为可以用细绳测量，即以细绳贴着叶子环绕一圈，然后将绳子拉直，再用尺子测量绳子长度，就能得出叶子的周长。笔者将提前准备好的叶子和细绳分发给学生，鼓励他们动手操作。在测量过程中，笔者还提出一系列问题启发学生思考自己的操作是否正确，如测量的准确位置应该在哪里？不测量满一圈可以吗？超过一圈可以吗？一番操作下来，学生扎实掌握了叶子周长的测量方法。为了进一步增强学生对周长的认知和感悟，积累大量的周长测量经验，笔者要求学生随手选择自己的学习用品进行周长测量，如课本、铅笔盒、三角板、水杯盖等。在对不同物品周长测量的操作中，学生深入理解了周长概念中蕴含的变曲为直的重要数学思想，初步确立周长的概念。

数概念作为小学数学中的一项基本内容，其学习可分为两个阶段，第一阶段是过程操作，第二阶段是对象形成。这两个学习阶段均需要以操作运算作为基础，因此动手操作是学生学习概念、理解法则和掌握新知的重要途徑。但由于数概念本身较为抽象，而小学生的思维仍然以具体想象思维为主，他们在学习时存在一定的难度，所以教师在设计动手操作任务时应当紧密结合学生熟悉的生活，让学生能够准确领会动手操作的目的，迅速发现操作的思路，在操作中建构概念、激发数感。

二、立足应用，在运算中发展数感

小学生学习数学处于起步阶段，数感刚刚建立，对数量、数量关系、运算结果估计方面的感悟还比较浅显，教师应该在教学中立足数的实际运用，给予学生更多的实际操作及应用机会，让他们在不断解决问题的过程中积累数学经验，逐渐发展对数的理解与感悟。“运算”在小学数学中主要指代数的运算，运算类型的题目为学生提供了相当多的应用机会;另外“运算能力”也是课程标准中明确规定要培养的学科能力之一，主要指能够根据法则和运算律正确地进行运算的能力。由此，在小学数学课程中注重运算的教学，有利于增强学生对数字和不同运算方法的熟悉度，提升学生在运算结果估计方面的能力，为他们此后探究更复杂的数量关系奠定基础。

例如，在教学人教版数学五年级上册《小数乘法》一课的“积的近似值”内容时，笔者立足于实际情况，设计了一些运算题目，如小明想去学校的跑道跑2圈，假设他每分钟可以跑199.8米，跑道是400米的，那么用什么简单的方法可以知道他跑完2圈大约需要的时间？有的学生直接用400×2÷199.8，最终四舍五入得出4分钟的运算结果。然而这样的运算过程相对复杂，笔者提示学生往估算方面想一想。部分学生得到启发，先将199.8米/分钟≈200米/分钟，得出跑完1圈所花费的时间就是400÷200≈2分钟，最后跑完2圈就应该是4分钟。估算法作为数学运算中一种重要方法，其应用相当广泛、灵活，通过多用多练，学生自然能够判别在运算时是否需要使用该法，这是数感建立的一种体现;另外，估算方法相对简单便捷，往往口算就能得出结果，学生在口算的过程，自然而然会增加对估算的感悟，这对其数感的形成也极有裨益。

又如，在学习人教版数学三年级下册《小数的初步认识》一课时，学生较易在数的进位、退位上出现错误。于是，笔者设计了一道实用性较强的运算题目：妈妈给了小明20元钱，让他去超市买1瓶酱油、1双袜子、1颗棒棒糖。小明去到超市一看，酱油是11.9元1瓶，袜子是6.2元1双，棒棒糖是1.5元1颗。请问小明的钱够用吗？具体要用多少钱？一名学生首先采用估算的方法解决第一个问题：11.9元估为12元，5.2元估为6元，二者相加后再加上1.5元约等于19.5，所以钱是够用的。另一名学生在计算具体钱数，即计算11.9+6.2+1.5时，分位数相加忘记向前进1位，导致算出18.6元的错误结果。根据此错题，笔者相机渗透小数估算以及小数进退位的方法，同时提供大量类似的练习题，如计算1.3+7.9+15.6，4.4+9.7+3.9，20-7.1+11.2，19.4-3.9-7.7等题目，提升学生对小数加减法应用的熟练度，同时增加其对此类题型的解题经验。

总结而言，运算的目的是寻找合理简洁的运算途径解决问题，而立足实际应用，能引导学生在具体的情境中厘清计算思路，迅速找到适宜的运算方式，或者让学生在实践中不断纠正错误，总结正确解题经验。因此，教师应该重视日常运算的训练，促进学生在运算中提升能力、发展数感。

三、简化抽象，以建模强化数感

数学建模是一种数学思维方式，是指利用数学语言、数学方法将问题抽象概括成一个数学模型。利用数学模型解题，是一种将复杂的数学问题简化再解决的方式。数感虽是一种抽象表述，但能表现在利用数学方法解决实际问题的能力上。因此，指导学生掌握数学建模的方法，实际上是训练学生解题的能力，强化学生的数感，教师应当根据教学内容的不同，灵活进行数学建模教学。

数量关系的运用是小学数学教学中一项重要内容，也是小学阶段常用的数学建模形式之一。不同年级的教材中均相应安排体现数量关系的应用题内容，如“部总关系”“份总关系”“相差关系”、速度问题、周长面积计算公式等。当学生学习了多种数量关系后，容易出现知识上的混淆。笔者在执教二年级数学时，发现学生对之前学过的“部总关系”较为熟悉，当接触到“份总关系”“相差关系”等更多关系种类后，在分析应用题目时容易受到干扰，造成答題错误。对此，笔者在设计题目时有意识地增加一些“干扰”，并指导学生通过提取题目给出的信息建立正确的数学模型。如题目“红球有7个，白球有6个，绿球是红球的2倍，请问绿球有几个？”，如果学生没有仔细审题，提取出错误的信息，那么所建立的倍数关系数学模型就会出错，最终得出6×2=12的错误答案。如果仔细审题，学生便能发现白球的信息完全是多余条件，正确的计算应当是7×2=14。这样设计的目的在于培养学生的信息收集能力和辨析能力，帮助学生准确找到问题中的有效信息，建立正确的数量关系，增强数感。

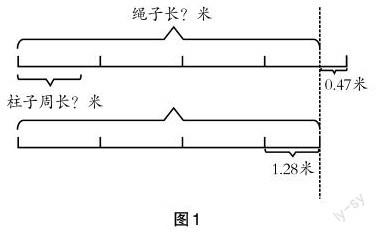
分析数量关系能够直接获得有效信息，但复杂的应用题中往往包含着多个数量关系，这对学生筛选、分析和建立信息之间的关联会造成更大的难度，此时利用图示法帮助学生分析问题，是一种很好的数学建模形式。如一道题目：利用绳子测量柱子的周长，如果绕4圈，那么还少0.47米，如果绕3圈，又多出1.28米，请问这根绳子的长度是几米？学生审题后一时之间不知如何入手，笔者提示可根据题目绘制线段图来分析（如图1）。

以上线段图就是分析题目数量关系的直观模型，通过观察模型，学生很快理解了绕4圈不足的0.47米和绕3圈多出的1.28米相加就是一圈或者一份的长度，因此柱子的周长是0.47+1.28=1.75（米）。由此可见，模型是直观呈现数量关系的载体，教师在教学过程中有意识地将数学问题抽象简化为数学模型，有利于学生读懂题意、理解题意，增强对数量关系的感悟。

总之，在小学数学教学中培养学生的数感，应将重点落在帮助学生学用数学的思维去思考问题、理解问题和解释问题。在实际的教学中，教师紧密联系实际生活、加强应用训练、抽象简化问题等具体方式，是培养小学生数感行之有效的课堂策略。

【作者简介】梁 君（1981— ），女，汉族，广西玉林人，大学本科学历，一级教师，现就职于玉林市玉州区大北小学，主要研究方向为小学数学教育。

（责编 黄健清）