双线重载铁路隧道仰拱与填充层动力响应分析
刘 洋 李兆琦 张朋天 王小敬 王永亮
(1.河北建筑工程学院土木工程学院,河北 张家口 075000;2.北旺集团有限公司,承德 067000;3.青海省交通控股集团有限公司,青海 西宁 810003)
0 引 言
重载铁路的出现进一步优化了交通运输系统、降低了运输成本、提高了运输效率,但截止到2019年年底全国的重载列车总长还不足普速铁路的十分之一[1].在我国交通运输线路不断优化的背景下,重载铁路将会继续发展,从而让运输条件更加科学合理.
国内有不少学者研究过各种荷载下隧道的动力响应,如黄娟等[2]从振动微分方程中得到荷载在移动时的计算方法,认为仰拱和边墙是隧道动力设计的薄弱部位.董军等[3]对无空洞条件和组合空洞条件隧道结构在振动荷载作用下进行了数值分析,认为单一拱腰空洞条件影响衬砌结构最大主应力的主要因素.王会永[4]认为列车轴重增加,各项指标(除轮重减载率以外)均随轴重的增加有较大增幅.陈晨[5]在对不同工况的动力响应特性分析后,认为仰拱是隧道受振动影响的最不利位置,响应规律为仰拱到拱顶逐渐变弱.陈卫军等[6]认为控制结构设计的是土压静载值,由车致荷载引起的附加内力增量相对较小.于丰泽[7]认为采用指数曲线法预测动载下的沉降量较合理.白冰等[8]认为列车运行时,列车正下方的隧道结构加速度响应、轴力峰值都为最大.
本文主要是根据建立的单洞双线隧道动力分析模型,对比分析重载列车运行时隧道中轨下仰拱处与仰拱中心的动力响应规律从而判断仰拱的最不利位置,通过应力云图整体分析了隧道填充层的动力响应特性.
1 模型建立
1.1 模型计算及参数
模拟环境以某铁路作为参考,隧道模型为单洞双线隧道,设计洞跨14m,隧道计算范围为水平方向以隧道中线为中心左右两侧各50m作为模型边界,竖直方向自隧道底部向下36m作为模型边界,自隧道顶部向上16m作为模型边界.隧道设计计算模型如图1所示.
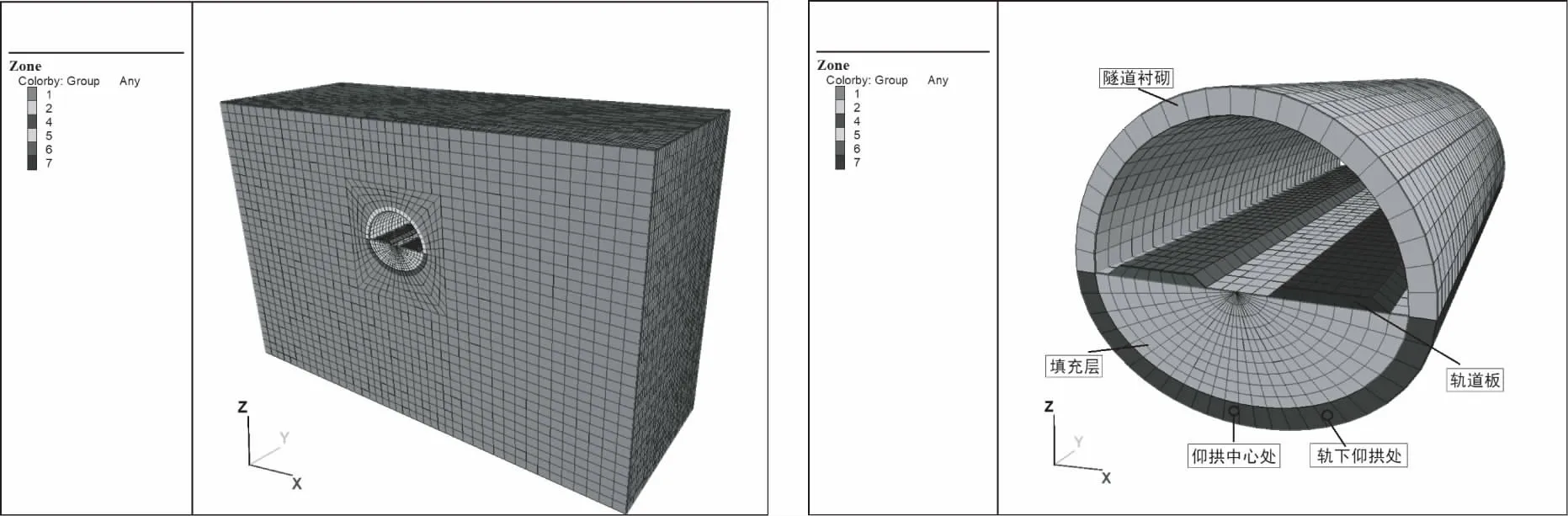
(a)整体模型 (b)隧道结构模型
围岩采用实体单元模拟,材料符合弹塑性模型和Mohr—Coulomb屈服准则,隧道填充、衬砌支护、轨道板采用实体单元的线弹性材料进行模拟,各参数的具体取值见表1.

表1 围岩及结构物理力学参数
体积模量K和剪切模量G都与弹性模量E和泊松比v有关,具体为式(1)、(2).
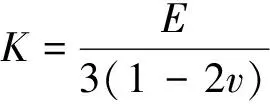
(1)
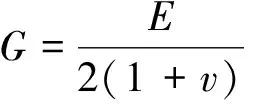
(2)
1.2 荷载的施加
进行数值模拟计算时使用激振力函数[9-10]来模拟重载列车振动荷载作用力,并将此力施加在位于隧道填充层中线两侧的轨道板上.该函数所计算的动荷载包括静荷载和三部分正弦函数,同时考虑了列车轴重、非悬挂质量等影响因素,可以在一定程度上模拟列车荷载,具体表达式为:
F(t)=P0+P1sinω1t+P2sinω2t+P3sinω3t
(3)
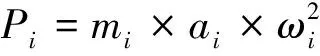
(4)
ωi=2πV/Li
(5)
式中:P0—车轮静载(kN);P1,P2,P3—振动荷载(kN);mi—列车簧下质量(kg);ai—相应于不平稳控制条件下的几何不平顺矢高(m);ωi—动圆频率;V—速度(m/s);Li—不平顺曲线的波长(m).列车簧下质量为mi时可根据表达式(4)来确定相应振动荷载的数值,根据铁路设计规范,以工况25t轴重的列车为例,取单边静轮重125kN,簧下质量m0=1000kg,计算车速为60km/h,列车连续通过轨道.圆频率计算式为(5).
在实际情况中,每组轮载通过钢轨、轨枕的传至道床表面,但是上述公式并未考虑轨道对列车荷载的分散作用.对此,引入传递系数k1(一般取1.2~1.7)与分散系数k2[11](一般取0.6~0.9),将式(3)修改成式(6).
F(t)=k1k2(P0+P1sinω1t+P2sinω2t+P3sinω3t)
(6)
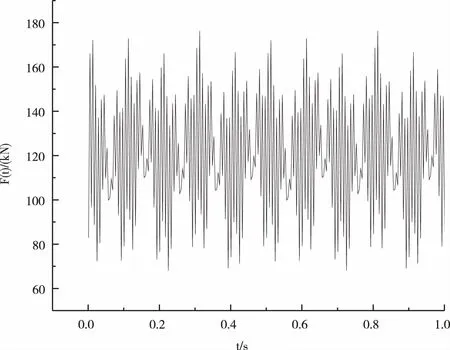
图2 激振力与时间关系图
动力荷载形式采用了TABLE命令定义的表,通过在相邻轨枕上施加一定时间间隔的激振力来反映列车沿着轨道运行时发生的瞬时空间位置变化,如图3所示.假设轨枕间隔为L0,两相邻轨枕时间间隔为t0,各轨枕上的列车振动荷载为Pn(t),表达式为式(8).
t0=L0/v
(7)
Pn(t)=F(t+nt0)
(8)
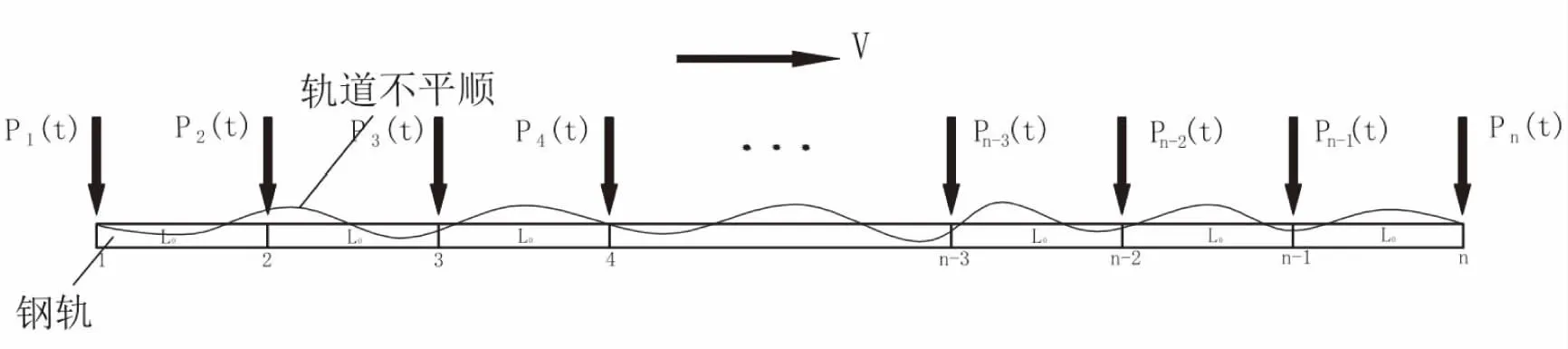
图3 荷载加载示意图
论文设计计算条件为:两条轨道板均距离隧道填充层中线1m均匀铺设,在每块轨道板上施加两条动荷载,围岩以V级围岩考虑.根据研究目的共设计了轴重25t的列车、轴重30t的列车两种工况,通过这两种工况来研究轨下仰拱与隧道仰拱中心的动力响应规律以及填充层的动力响应规律.
2 计算结果分析
2.1 填充层动力响应分析
填充层在动力荷载作用下受力情况较为复杂,通过填充层的主应力云图来整体研究它的动力响应规律.在25t重载列车荷载作用下填充层的主应力云图如图4所示,动荷载作用下的填充层所受最大拉应力为1.81MPa,位于填充层的上部局中的部位;所受压应力最大值分别为2.79MPa,位于填充层两侧.可以发现,在沿隧道中线铺设的两条轨道板上同时加动荷载模拟单洞双线列车行驶时,填充层内部受力非常复杂,从图4(a)最大主应力云图可以看出其中间部分所受较大的拉应力,图4(b)最小主应力云图可以看出两端和底部都有较大的压应力.填充层的压应力峰值略大于拉应力峰值,且拉应力最大值出现在填充层中线部分,考虑到混凝土的抗拉强度远小于抗压强度,所以该双线隧道的隧道中线附近区域为填充层结构的最不利区域.
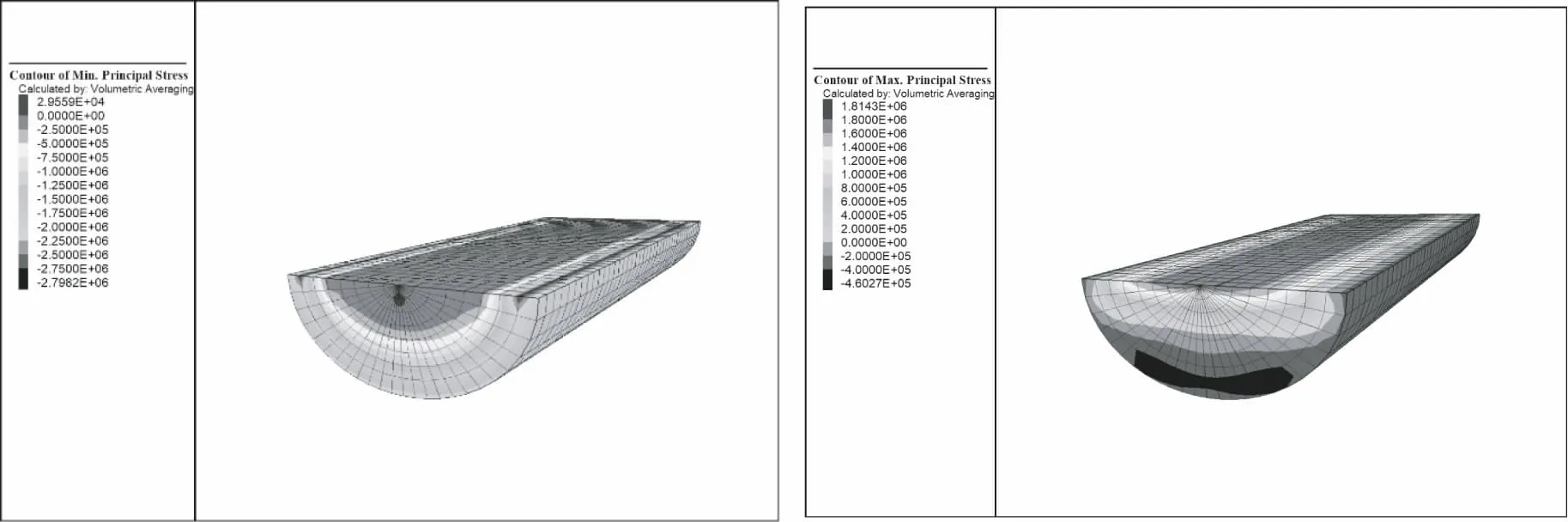
(a)最大主应力 (b)最小主应力
2.2 仰拱动应力分析
为研究轨下仰拱处和仰拱中心两处竖向动应力变化规律,分别模拟计算了车速为60km/h的25t轴重列车和车速为50km/h的30t轴重列车两种工况.沿轨道方向的竖向动应力峰值大小如图5所示.
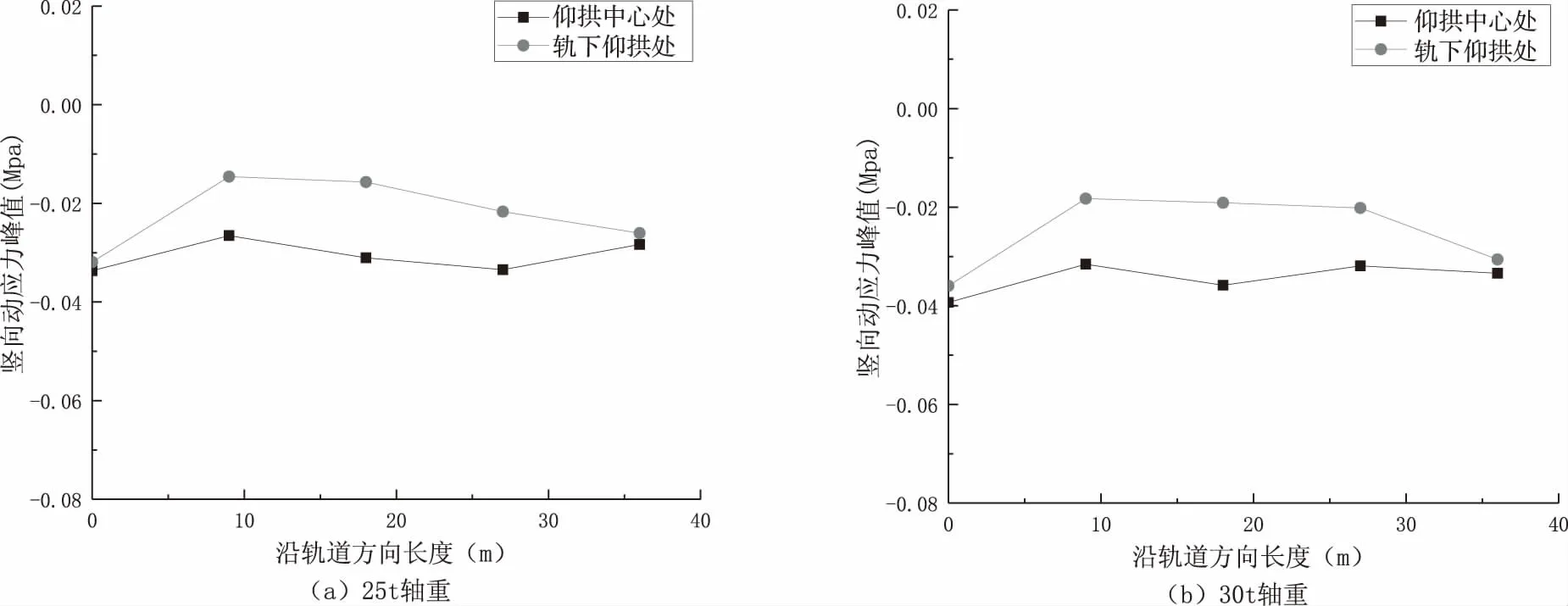
图5 竖向动应力峰值曲线
从图5的结果可以看出,车速为60km/h的25t轴重工况下仰拱中心处的竖向动应力峰值在-300kPa上下波动,轨下仰拱处竖向动应力在-190kPa上下波动,中心处的动应力峰值比轨下处增加了约54%;车速为50km/h的30t轴重工况下仰拱中心处的竖向动应力峰值在-350kPa上下波动,轨下仰拱处竖向动应力在-200kPa上下波动,中心处的动应力峰值比轨下处增加了约58%.总体来看,在同一深度下沿轨道方向的应力峰值变化规律基本相同.可见轨道中心处承受较大的动应力,所以仰拱中心处更容易发生破坏.
2.3 仰拱应力响应分析
为分析轨下仰拱处和仰拱中心处的应力响应规律,在两线路中线下方的仰拱处和单侧轨道下方布置了测点,测得的应力时程曲线见图6.以25t轴重列车的工况为例,两条线路同时施加列车荷载,隧道仰拱处中心处及轨下仰拱处大、小主应力响应规律基本相同,由图6可知,仰拱中心处和轨下仰拱处最大主应力峰值分别为0.898MPa、0.85MPa,最小主应力峰值分别为-19.46kPa、-19.33kPa;仰拱结构拉应力远大于压应力,说明仰拱结构受力情况为以受拉为主,破坏受抗拉强度控制.两轨道中线处的大小主应力之差最大,由最大剪应力理论可知,该处仰拱受到的剪应力最大,仰拱中心处应适当增大配筋率.
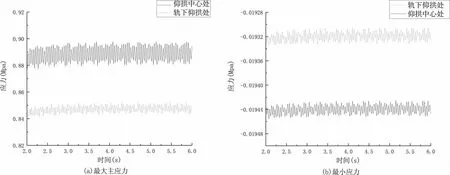
图6 仰拱大小主应力时程曲线
2.4 仰拱加速度响应分析
隧道竖向所受重载列车的振动荷载作用,分别设计计算了同一车速下25t轴重列车和30t轴重列车两种工况的仰拱加速度值,时程曲线如图7和图8所示,加速度时程曲线为一定周期的波状线且每个周期的波峰基本相同,各工况仰拱中心处、轨下仰拱处的加速度峰值见表2.
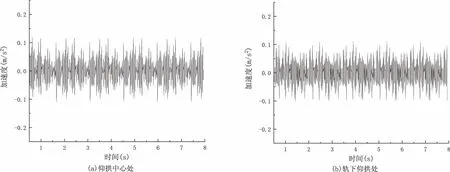
图7 25t轴重列车振动荷载下加速度时程曲线
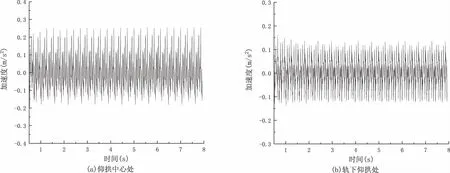
图8 30t轴重列车振动荷载下加速度时程曲线
由表2可以看出,在同一工况下仰拱中心处、轨下仰拱处的加速度的时程曲线基本相似,数值大小不同,仰拱中心处的加速度比轨下仰拱处要高出了约1.5倍,且加速度的值也会随着轴重的增大而变大.

表2 不同轴重列车动力响应下加速度时程曲线峰值
3 结 论
本文主要是研究单洞双线隧道在动荷载作用下仰拱和填充层的动力响应规律,根据数值模拟结果可以得到以下结论:
(1)重载列车振动荷载作用下的隧道填充层结构受力复杂,最大拉应力值出现在填充层上部的中线部位,最大压应力值主要分布在填充层两端和底部,两条线路的中线附近区域为填充层结构的最不利区域.
(2)双线隧道在同种列车荷载作用下,仰拱结构所受拉应力远大于所受压应力,破坏受抗拉强度控制,两线路中心处的仰拱竖向动应力峰值比单侧轨道下方的仰拱动应力峰值高出了约58%,加速度比单侧轨道下方高出了约1.5倍,受到的拉应力和剪应力相较于仰拱其他部位也为最大,双线隧道的仰拱中心处应适当增大配筋率并加强安全支护设计.
(3)不同列车轴重下仰拱和填充层结构动力响应规律基本相同,随着轴重的增大,仰拱及填充层的主应力、加速度、竖直方向的动应力都有明显的增加.
——以淮南矿区为例

