不同负温下冻结粉土的力学特性研究
杨尚礼 赵 嘉
(河北建筑工程学院土木工程学院,河北 张家口 075000)
0 引 言
在中国,冻土分布很广.青藏高原、西北高山和东北北部的大、小兴安岭及松嫩平原等地区分布着大片多年冻土,面积约215万km2,占国土面积的22.4%[1]因此在冻土区修建工程必不可免,而冻土的特殊性又造成了冻土工程的特殊性.
目前国内针对冻土的研究主要集中在外加剂、围压、强度、正融、影响因素等方面.牛亚强等[2]研究黄土、石灰改良黄土及水泥改良黄土在-6℃负温下不同围压作用下的变形规律和强度特性,为今后改良黄土在寒区工程中的应用提供可靠的理论参考.刘琳[3]进行了冻土的单轴无侧限抗压强度试验,研究得出含水量、冷却温度、融化温度是影响冻土强度弱化的重要原因.陈雨漫[4]研究冻结粘土力学性能参数及其变化规律,得出在-15℃~-5℃范围内,冻土的弹性模量、单轴抗压强度、黏聚力均随温度降低而增大,而泊松比随温度降低而减小;在低应力条件下,冻土蠕变基本上属于稳定性蠕变;在高应力条件下,试验结果属于非稳定性蠕变.李晓刚等[5]进行室内冻土单轴抗压强度试验结果表明:相同负温下中粗砂抗压强度最大,其次是粉细砂、粉质黏土、黏质粉土,杂填土抗压强度最小;土体负温越低,抗压强度越大.李蓬勃等[6]研究负温对冻结作用下黏土强度的影响,研究结果表明随着负温的降低,冻土单轴抗压强度逐渐增大,增加幅度逐渐减小.平永庆等[7]研究含盐冻结砂土单轴压缩试验,结果表明砂土的结冰温度随着含盐量的增加而降低,含盐量大于3%,变化明显;-10℃冻土单轴抗压强度随着含盐量的增加强度降低显著.蔡正银等[8]研究冻结状态下渠基土的物理力学特性,结果表明单轴抗压强度随温度的降低线性增加.尹珍珍等[9]研究影响冻土抗压强度的因素得出影响程度由大到小依次为温度、加载速率、含水率.
综上所述,前人研究高粉粒含量下冻土力学性质较少,而粉粒含量的多寡对土体的冻结有着重要影响进而影响冻土的力学性质,本文研究在高粉粒含量下(60%粉粒含量)土体在不同冻结温度,不同围压下的力学性质.
1 材料与方案
1.1 试验方案
试验土样取自张家口某建筑工地,分别经过0.075 mm和2 mm筛子筛分后按照实验计划比例混合,粉粒含量混合比例为60%,按照《土工试验方法标准》(GB/T 50123-2019)进行击实试验,通过击实试验测得粉粒含量为60%的土样最优含水率为17.5%,最大干密度为1.691 g·cm-3,击实试验结果如下图所示.本文研究不同负温下土体的力学性质,负温设定为0℃、-5℃、-10℃、-15℃,围压设定为50 kPa、80 kPa、120 kPa.

图1 干密度与含水率关系图
1.2 试样制备
将取回土样在105℃烘箱中烘干24 h后,经0.075 mm和2 mm筛子筛分后按照实验计划设定进行不同粒径土样混合,按照击实试验测得最优含水率制备土样,使用保鲜袋闷料24 h,冻土三轴试件按照《土工试验方法标准》(GB/T 50123-2019)进行制备,试样直径为61.8 mm,高度为125 mm,试样冻结过程在高负温交变箱中进行,将试样连同橡胶模一同放入高负温交变箱中在-30℃的负温下快速冻结24 h,然后调节高负温交变箱温度至试验温度冻结24 h.
1.3 试验设备与试验步骤
冻土三轴试验在冻土三轴仪上进行,将试样从高负温交变箱取出放入压力室内的底座.安装冻土三轴压力室,外腔与内腔迅速充入设定温度的防冻液,在设定负温下恒温2 h,然后施加计划围压,维持2 h,试验加载速率为1 mm/min,当试样产生15%应变时停止试验.试样取下后仍然保持冻结状态,冻土三轴试验成功.试验仪器与试验后试样分别见图2,图3.

图2 试验仪器 图3 试验后试样
2 试验结果与分析
2.1 应力应变关系
本文以不同负温影响下的应力应变曲线关系展开分析,如图4所示,从图4中可以看出0℃试件应力-应变曲线均为硬化型,随着冻结负温的下降,应力应变曲线为软化型,试样的破坏由塑性破坏转换为脆性破坏.从图中可以看出,随着负温的降低,三轴偏应力也在增加,二者呈现正相关关系.从图4中可以看出,围压只改变三轴试样的强度,并未改变应力应变曲线的形式;当三轴试验温度较低时(-5℃以下)试样应力-应变曲线均可分为三个阶段,线性增长阶段,此阶段应变范围在0~3%,在此阶段,应力增长较快,应力应变曲线近似成为一条直线,在此阶段,试样呈现弹性体性质;非线性缓慢增长阶段,此阶段出现在应变范围3%~5%,在此阶段试样表现出非线弹性性质,在此阶段末,峰值偏应力出现;试样破坏,应力缓慢趋于稳定阶段,此阶段应变范围在5%~15%之间,表现为偏应力随着试验时间的增长而缓慢趋于稳定出现残余应力.从图4中可以看出,随着负温的下降,试样残余应力也在逐步上升.

图4 不同负温影响下的应力应变曲线关系
2.2 负温对峰值偏应力的影响
图5为负温与试样峰值偏应力的关系曲线,从图5可以看出随着负温的降低,各试样峰值偏应力增大,二者呈现正相关关系.分析因为土体冻结后,大部分孔隙水冻结成冰,充满孔隙,将周围的土颗粒粘结在一起,使颗粒间的粘聚力大大提高,从而提高了冻土的强度,而随着负温的降低,越来越多的孔隙水凝结成冰,其冻结强度大大提高,随之峰值偏应力也大大提高.
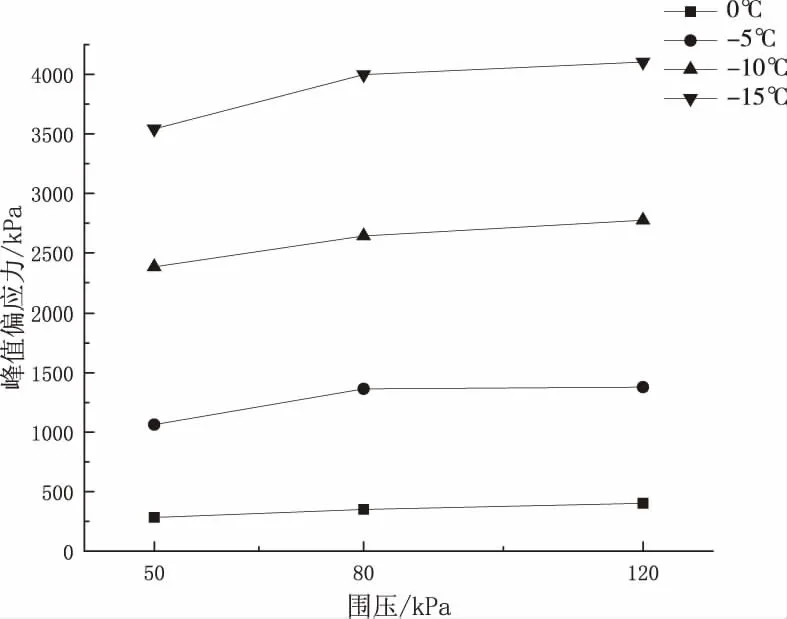
图5 负温与峰值偏应力关系曲线
2.3 负温对残余强度的影响

图6 残余强度变化曲线
由图4可以看出峰值过后应力大致稳定在15%应变时,取15%应变时对应应力为试样残余强度,试样残余强度随负温的变化曲线如图6,从图中可以看出,试样的残余强度随着围压的增大而增大,随着负温的降低而增大,且随着负温的降低增大的更迅速,分析原因是因为围压在三轴试验中起到了“围箍”作用[10],使冻土在压力的作用下更加密实,从而使残余强度增大.随着负温的增加,冻土中冰晶体数量逐渐增长,增强土颗粒之间的胶结力,进而增强土体冻结强度,从而使残余强度增大.
2.4 负温对抗剪强度指标的影响
图7给出了负温与抗剪强度指标的变化关系,从图7中可以看出,粘聚力随负温降低呈现线性增长,负温对内摩擦角的影响较小,虽呈现上升趋势,但是增长缓慢,波动很小.60%粉粒含量试样粘聚力及内摩擦角均随着负温的降低呈现上升趋势,分析原因是因为随着温度的降低,试样中未冻水的含量减少,试样中含冰量增大,冰晶增多使得其胶结力增大,所以土样粘聚力和内摩擦角增大.

图7 负温与抗剪强度指标关系曲线
3 邓肯-张模型参数
邓肯-张模型根据双曲线应力应变关系提出,是建立在增量广义胡克定律基础上的变模量的非线性弹性模型,由于其参数少、物理意义明确,并能更好的反映土体力状态应力-应变本构关系.-5℃、-10℃、-15℃试样应力应变曲线均为软化形,曲线峰值前为非线性弹性段,峰值后为破坏阶段,而邓肯张模型为非线性弹性模型,故文章选取(-5℃、-10℃、-15℃)三个冻结温度下应力应变曲线的峰值前部分进行邓肯张-模型分析.应力应变曲线均为有峰值点情况,破坏比Rf均取1.
3.1 初始变形模量的求取
将图4的应力应变曲线关系按照双曲线模型拟合如图8所示,双曲线模型为:

(1)
其中a为直线截距,b为直线斜率.


图关系曲线
通过图8,可以得出不同冻结温度下a、b、初始弹性模量值如表1,从表中可以看出,随着冻结温度的降低,直线的截距(a值)和斜率(b值)逐渐减小,起始变形模量逐渐增大.

表1 不同冻结温度a、b、起始变形模量值1/a
3.2 不同冻结温度下K、n值确定
拟合lg(Ei/Pa)与lg(σ3/Pa)的关系图,拟合的关系接近直线,如图9所示,可得

(2)
直线方程为:
lg(Ei/Pa)=lgK+nlg(σ3/Pa)
(3)
式中Pa为大气压强,取值为101.4kPa.从图中可以看出截距(K值)和斜率(n值)都随着冻结温度的减小而增大.

图9 lg(Ei/Pa)与lg(σ3/Pa)关系曲线
对不同冻结温度下的K值进行拟合,K值与冻结温度成线性函数关系,其函数式子为(4).
K=-0.567T+2.7755
(4)
对不同冻结温度下的n值进行拟合,n值与冻结温度成线性函数关系,其函数式子为(5).
n=-0.0311T-0.1445
(5)
试验得出的材料常数K、n与通过函数关系式预测得出的材料常数K、n如表2所示,从表2可以看出实测值与预测值较为吻合.

表2 材料常数K、n实测值与预测值
式(6)为邓肯-张切线变形模量公式,将式(4)和式(5)代入式(6)中,可得到式(7)关于不同冻结负温的Etd,Etd包含6个材料常数K、n、φ、c、Rf、T.
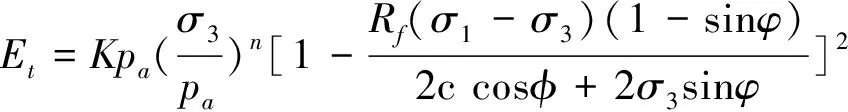
(6)

(7)
以-5℃试样为例对式(7)得出预测值与实际值进行对比,结果如图10所示,邓肯-张模型计算值与实验值基本吻合.

图10 模型预测值与实际值对比
4 结 论
通过研究不同负温,不同围压下土体三轴试验应力应变曲线,主要有以下结论.
(1)随着负温的降低,试样应力-应变曲线由硬化型转换为软化型,试样的破坏由塑性破坏转换为脆性破坏,随着冻结负温的降低,三轴偏应力峰值也在增加,二者呈现正相关关系.
(2)研究了随着负温的降低,试样峰值偏应力及残余强度逐渐增大.
(3)分析了土体三轴抗剪强度参数与负温的关系,随着温度的降低,试样内摩擦角的增幅较小,负温对试样粘聚力的增长影响较大,这与随着温度下降,试样强度上升现象一致.
(4)将应力应变曲线的峰值前部分进行邓肯张-模型分析,得出参数a与参数b随冻结温度的下降而减少,起始变形模量随冻结温度的下降而增大.建立了以不同冻结温度为影响因素的冻结粉土邓肯-张模型,并将预测值与实测值进行对比,二者基本吻合,邓肯-张模型能很好的反映出冻结粉土的本构关系.

