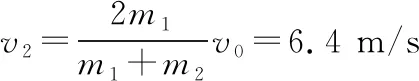四种常用数学方法求解物理极值问题
安徽
在处理求极值的物理问题时,往往需要一些数学知识,比如二次函数、基本不等式、半角公式、辅助角公式等,根据它们的规律,找到物理量的极值。
1.解题思路
根据物理情境,发现物理规律,从基本问题出发,写出所求物理量的表达式,这是关键一步。然后根据表达式的形式选择所需要的数学知识求得极值。
2.数学知识

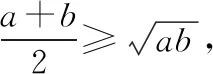
3.典例透析
【例1】(二次函数求极值)如图所示,光滑绝缘的正方形水平桌面边长为d=0.48 m,离地高度h=1.25 m。桌面上存在一水平向左的匀强电场(除此之外其余位置均无电场),电场强度E=1×104N/C。在水平桌面上某一位置P处有一质量m=0.01 kg、电荷量q=1×10-6C的带正电小球以初速度v0=1 m/s向右运动。空气阻力忽略不计,重力加速度g取10 m/s2。求:
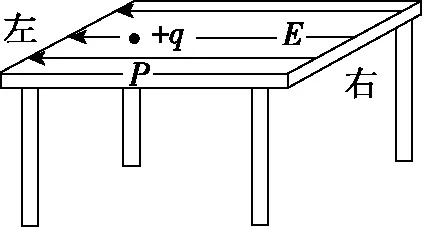
(1)小球在桌面上运动时加速度的大小和方向;
(2)P处距右端桌面多远时,小球从开始运动到最终落地的水平距离最大?并求出该最大水平距离。
【解析】(1)对小球受力分析,小球受到重力、支持力和电场力作用,其中重力和支持力平衡,根据牛顿第二定律,有qE=ma
解得a=1.0 m/s2
方向水平向左
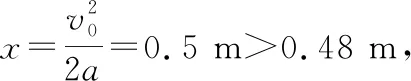
设小球到桌面右边的距离为x1,小球离开桌面后做平抛运动的水平距离为x2,则
x总=x1+x2



代入数据得t=0.5 s
水平方向,有
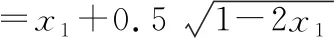




【例2】(基本不等式求极值)如图所示,在粗糙水平台阶上静止放置一质量m=0.5 kg的小物块,它与水平台阶表面间的动摩擦因数μ=0.5,且与台阶边缘O点的距离s=5 m。在台阶右侧固定了一个以O点为圆心的圆弧形挡板,并以O点为原点建立平面直角坐标系。现用F=5 N的水平恒力拉动小物块,一段时间后撤去拉力,小物块最终水平抛出并击中挡板(g取10 m/s2)。

(1)若小物块恰能击中挡板的上边缘P点,P点的坐标为(1.6 m,0.8 m),求其离开O点时的速度大小;
(2)为使小物块击中挡板,求拉力F作用的距离范围;
(3)改变拉力F的作用时间,使小物块击中挡板的不同位置,求击中挡板时小物块动能的最小值。(结果可保留根式)
【解析】(1)小物块从O到P做平抛运动,由平抛运动规律有,水平方向x=v0t
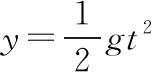
解得v0=4 m/s
(2)为使小物块击中挡板,小物块必须能运动到O点,设拉力F作用的最短距离为x1,由动能定理得
Fx1-μmgs=Ek-0=0
解得x1=2.5 m
为使小物块不会飞出挡板,小物块做平抛运动的初速度不能超过4 m/s;设拉力F作用的最长距离为x2,由动能定理得
解得x2=3.3 m
故为使小物块击中挡板,拉力F的作用距离范围为
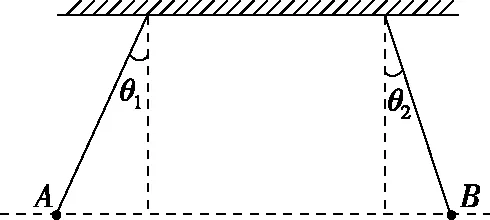
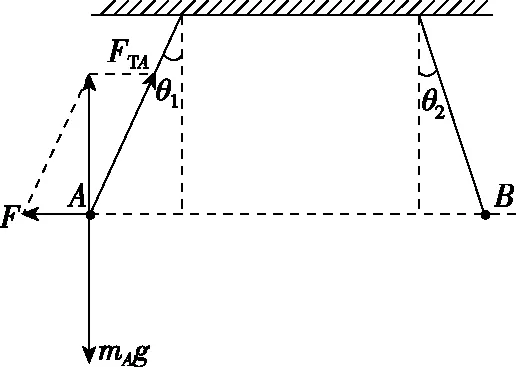
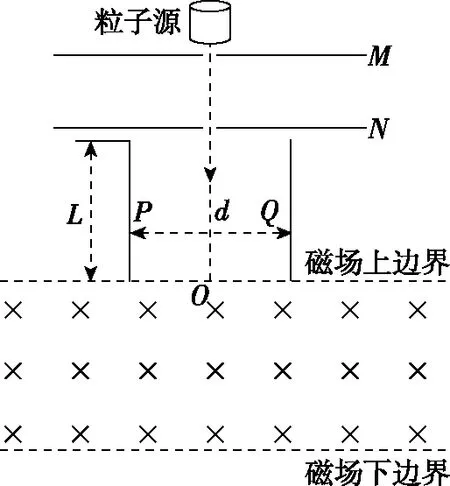
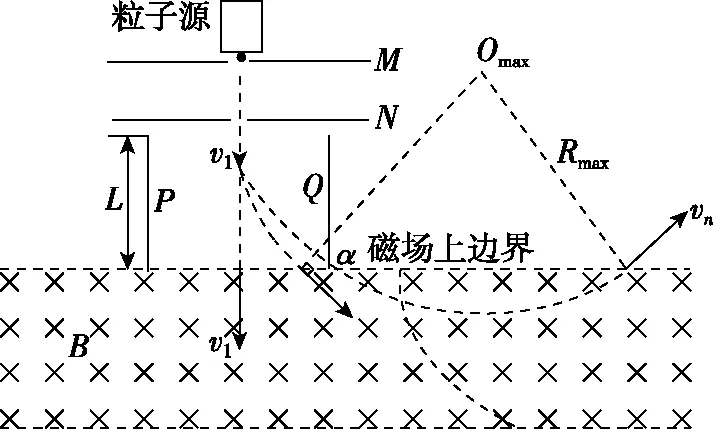
2.5 m 由动能定理得 又x2+y2=R2 由P点坐标可求得R2=3.2 m2 【例3】(辅助角公式求极值)如图所示,质量为M的木楔倾角为θ,在水平面上保持静止。当将一质量为m的木块放在斜面上时正好匀速下滑,如果用与斜面成α角的力F拉着木块沿斜面匀速上滑。重力加速度为g,下列说法中正确的是 ( ) A.当α=2θ时,F有最小值 B.F的最小值为mgsin 2θ C.在木块匀速上滑过程中,地面对M的静摩擦力方向水平向右 D.在木块匀速上滑过程中,地面对M的静摩擦力方向水平向左 【答案】BD 【点评】在外力F作用下,物体匀速运动时,F最小值的求解,首先根据受力平衡求出其表达式,其数学求解方法基本就是辅助角公式的应用。若采用摩擦角的方法求解过程会更简单(具体求解不再赘述,详见《四力作用下的动态平衡》微专题)。所以在处理物理极值问题时,优先选用物理方法。 甲 乙 (1)带电粒子进入偏转电场时的动能Ek; (2)磁场上、下边界区域的最小宽度x; (3)带电粒子打到磁场上边界感光胶片的落点范围的长度。 【解析】(1)带电粒子进入偏转电场时的动能,即为MN间的电场力做的功 Ek=WMN=qU0 (2)设带电粒子以速度v进入磁场,且与磁场边界之间的夹角为α时向下偏移的距离 Δy=R-Rcosα=R(1-cosα) v1=vsinα 当α=90°时,Δy有最大值(应用半角公式) 即加速后的带电粒子以v1的速度进入竖直极板P、Q之间的电场不发生偏转,沿中心线进入磁场。磁场上、下边界区域的最小宽度即为此时的带电粒子运动轨迹半径 (3)粒子运动轨迹如图所示,若t=0时进入偏转电场,在电场中匀速直线运动进入磁场时R=L,打在感光胶片上距离中心线最近为x=2L 任意电压下出偏转电场时的速度为vn,根据几何关系有 打在感光胶片上的位置和射入磁场位置间的间距始终相等,与偏转电压无关。在感光胶片上的落点宽度等于粒子在电场中的偏转距离,带电粒子在电场中的最大偏转距离 【点评】在本题中,以任意角度入射的粒子进入磁场后表示出向下偏移的距离,可以得出只有垂直入射的粒子向下偏移的距离最大,再由半径公式等即可解答第二问。在第三问中,由于带电粒子先经过电压为U0的加速电场,然后进入水平交变电场进行偏转,最后进入磁场做匀速圆周运动打在胶片上,可以表示出在任意偏转电压作用后做匀速圆周运动的半径表达式(其中速度用进入电场时的速度表示),再表示出打在感光胶片上的长度。巧合的是打在感光胶片上的位置和射入磁场位置间的间距始终相等,与偏转电场的电压无关,从而求出粒子在感光胶片上落点的范围。 1.(半角正切公式应用)如图所示,质量分别为mA和mB的两小球带有同种电荷,电荷量分别为qA和qB,用绝缘细线悬挂在天花板上。平衡时,两小球恰处于同一水平位置,细线与竖直方向间夹角分别为θ1与θ2(θ1>θ2)。两小球突然失去各自所带电荷后开始摆动。最大速度分别为vA和vB,最大动能分别为EkA和EkB,则 ( ) A.mA一定小于mB B.qA一定大于qB C.vA一定大于vB D.EkA一定大于EkB 【答案】ACD (1)求球1到达B点时对轨道的压力大小; (2)若球2的质量m2=0.1 kg,求球1与球2碰撞后球2的速度大小; (3)若球3的质量m3=0.1 kg,为使球3获得最大的动能,球2的质量应为多少? 【解析】(1)对球1从A到B由动能定理有 联立解得v0=4 m/s,FN=12 N (2)球1、球2的碰撞,根据动量守恒定律有 m1v0=m1v1+m2v2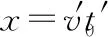
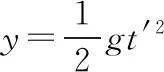

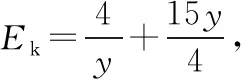





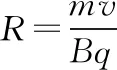

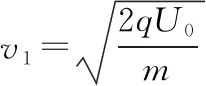
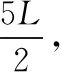
4.跟踪训练