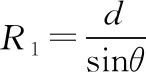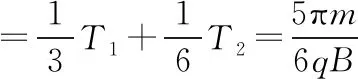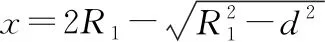以导函数应用专题复习为例谈数理思维的培养

新疆

应用数学方法寻找物理规律是物理学习的“硬”逻辑，物理中多数问题的解决依赖于物理公式，物理公式实际上就是各物理量之间的函数关系。做好数学知识在物理课堂中的有效应用，从而提升学生数理思维品质，是提升核心素养的重要途径。高中物理解决问题常用函数有一次函数、二次函数、三角函数、幂函数、导函数等，在高三二轮复习中专门以某种函数的应用为专题，实现数学和物理知识的整合，进而可取得良好的教学效果。

导函数的学习在高二上学期后期或高二下学期初期，学生的物理知识体系已基本完备，在新授课中的应用不多，在高三复习中以专题形式出现更加合理。在教学过程中，由于数学知识的不配套，导数相关问题教师更多的是以极限思想进行处理。建立以导函数的应用为主题的专题课，让学生从另一个角度理解物理概念、物理规律以及体会数学知识在物理中的应用，通过学科知识的相互渗透，培养学生的数理思维，从而达到提升学生核心素养的目的。导函数专题课可从重新释义物理概念、重新解释物理规律以及应用导函数解题三个方面进行。

1 重新释义物理概念

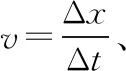
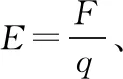
2 重新解释物理规律

在解释有些物理规律时，由于学生的数学知识匮乏常常用其他方式，如“零点定律”(物理量从零到零变化一定是先增后减)，这些方式体现着物理教师的教学智慧。到了高三再次对一些规律结合数学方法解释可以更加严谨，更加科学。

1.1 位移、速度、加速度的关系问题

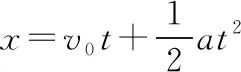
1.2 重力功率变化问题

小球与绳子成θ角从静止释放，运动到最低点过程中，重力做功变化问题，在初期教学中多数教师采取“零点定律”解释。最高点速度为零，重力功率为零，最低点重力与速度垂直，重力功率为零，所以重力功率先增后减。

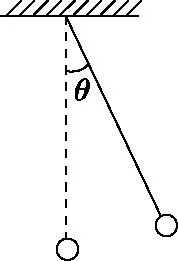
图1

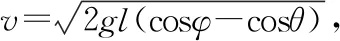
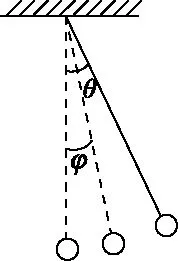
图2

1.3 等量同种电荷连线中垂线上场强变化问题

在初期教学中多数教师解释等量同种电荷连线中垂线上场强变化问题也是采取“零点定律”解释，等量同种电荷连线中点的场强为零，无穷远处的场强趋近于零，所以场强先增后减，最大值的位置不涉及或直接告知。

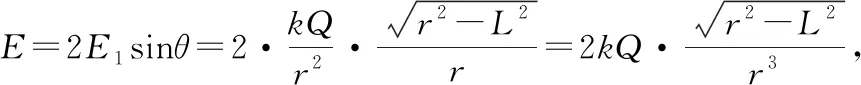
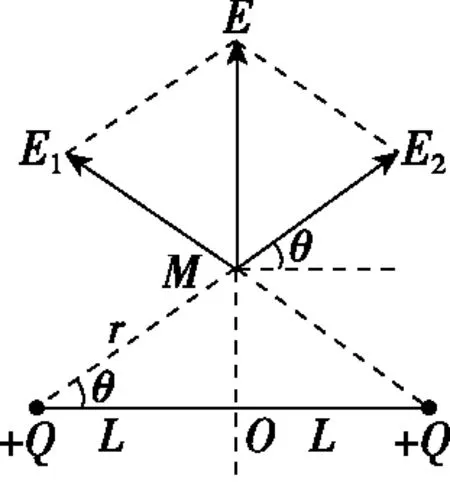
图3

1.4 电源的输出功率问题

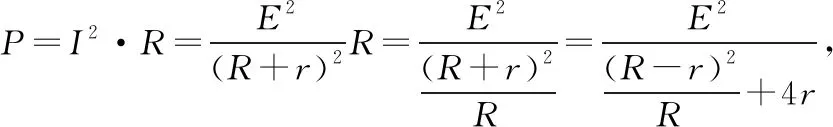
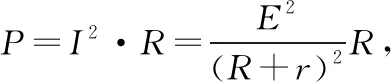
1.5 正弦式交变电流的变化规律问题

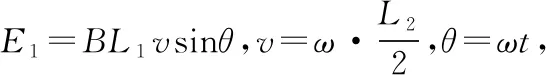
图4

若采用导数方法可以回归产生感应电流的条件，从磁通量的变化角度出发，应用法拉第电磁感应定律，使学生理解的更加深刻。正弦式交变电流从中性面开始计时，磁通量—时间关系Φ=BScosωt，求导得e=-BSω·sinωt，若线圈有N匝，则e=NBSω·sinωt。

3 讨论物理量的单调性和求极值

导函数在高三复习中最重要的应用是讨论物理量的单调性和求复杂问题的极值，在以上讨论的其他问题中导函数的应用并不会特别凸显出“优势”，只是为理解问题提供另外的思维方法。而在能写出函数关系的问题中采取求导的方式求极值和单调性，渗透数理思维，培养学生多种思路解决问题的能力显得尤为重要。

物理量的单调性问题常以两种形式出现，图像问题和具有定量关系的物理量变化问题。图像问题重点考查的是图像的“斜率”和“面积”的物理意义，而“斜率”正是“纵轴物理量”对“横轴物理量”的求导。常见的该类利用斜率来讨论物理量的单调性的图像有x-t图像、v-t图像、φ-x图像、Ep-x图像、Φ-t图像等。通过比较斜率的变化判断对应物理量的变化实际就是寻找物理量的单调性过程。大多具有定量关系的物理变化过程是较容易写出定量关系式的，通过求导的方式更容易找到极值和物理量的单调性。

【例】(2020年·新疆高三三模·25节选)如图所示，空间存在方向垂直于xOy平面向里的匀强磁场，在0d的区域Ⅱ内的磁感应强度大小为2B。一个质量为m、电荷量为-q的带电粒子(不计重力)，由静止经一电压可调的加速电场加速后从O点沿y轴正方向射入区域Ⅰ。

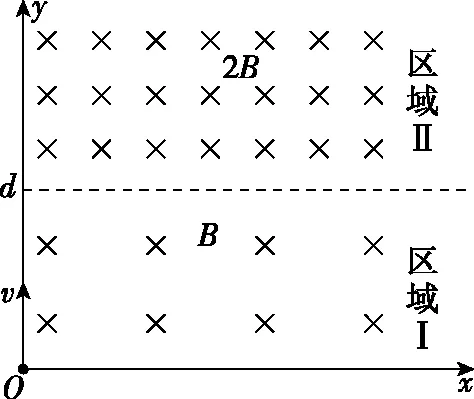
图5

(1)若粒子能从区域Ⅰ进入区域Ⅱ，求粒子从区域Ⅰ射出时打在x轴上位置坐标的最小值xmin，并求出此情况下粒子在区域Ⅰ中运动的半径R1；

(2)在满足(1)条件下，求出粒子在整个磁场区域内的运动时间t总。

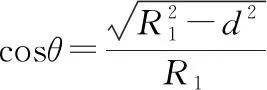
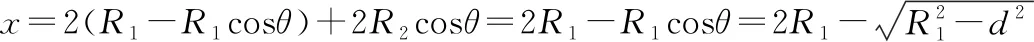
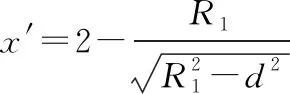
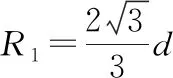
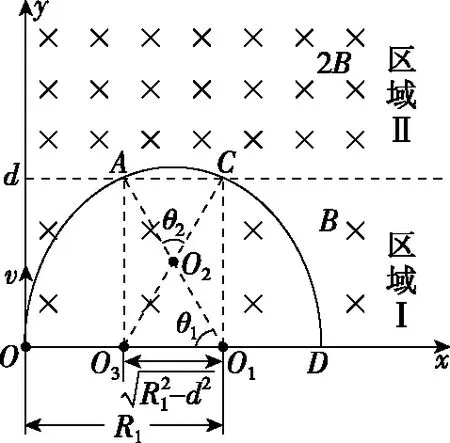
图6