七自由度仿人机械臂正逆运动学及工作空间分析

赵志亮，尹 猛，徐志刚，吴浩廷

(1.东北大学机械工程与自动化学院，沈阳 110819；2.中国科学院沈阳自动化研究所，沈阳 110016；3.中国科学院机器人与智能制造创新研究院，沈阳 110016；4.中国科学院大学，北京 100049)

0 引言

机械臂已应用于医学治疗[1]、抢险搜救[2]和深空探测[3]等领域。但传统机械臂惯量大、灵活性低，因此机械臂的减重、提高灵活性成为了一个亟需解决的问题。人体上肢小巧轻便、灵活性高，所以仿人机械臂现已成为机器人领域的研究热点之一[4]。

七自由度仿人机械臂体积小、重量轻、运动范围大，实现精准控制的前提是建立准确的逆运动学模型[5]。Kang T等[6]在分析骨骼系统冗余性的基础上提出了一种逆运动学迭代算法确定手臂姿势，但迭代过程非常复杂且耗时。Wang Y F[7]利用基于雅可比矩阵最优解的数值法求解运动学逆解，只能求出单一解，计算量大且无法体现机械臂的冗余性。崔泽等[8]利用向量投影法以及关节角的对应关系求解了机械臂逆运动学，但未进行优化导致运动过程中关节角发生突变。何兵等[9]利用差分进化算法求解机械臂运动学逆解，但建立的目标函数忽略了末端位置误差和姿态误差的权重，因此无法收敛到全局最优。Zhou D等[10]提出一种基于位置的方法来评估可行的逆运动学方案，通过外界的干扰来寻找最优解。段晋军等[11]以机械臂运动操作度最大原则将机械臂逆解转换为确定性问题，但是可操作度椭球的建立和θ的选取非常复杂。

本文以七自由度仿人机械臂为研究对象，利用D-H参数法建立正运动学方程。根据冗余机械臂SRS构型特性[12]，在给定末端位姿0T7和臂型角ψ的情况下，求得机械臂逆运动学8组解。在MATLAB环境中对机械臂正逆运动学方程进行可视化验证。最后运用蒙特卡洛法求解机械臂的工作空间云图。

1 仿人机械臂结构

仿人机械臂也称为关节型机械臂，是由一系列旋转关节和连杆组合成的一条开式运动链。图1展示了本文研究的七自由度仿人机械臂，由7个旋转关节串联及连杆组成。其中，自由度J1～J3形成肩部球关节S；自由度J4形成肘部；自由度J5～J7形成腕部球关节W[13]。仿人机械臂肩部固定于基座上，另一端在空间内自由运动，具有轻量化、响应快、精度高、工作范围大、安全性高等优点。

图1 7-DOF拟人机械臂结构简图

2 仿人机械臂正逆运动学分析

2.1 仿人机械臂运动学正解

D-H法以机械臂关节链中每个关节坐标系建立关节变化矩阵。以电机箱底部中心为原点建立基坐标系X0Y0Z0，根据机械臂结构可以得到机械臂各连杆坐标系以及D-H参数表。

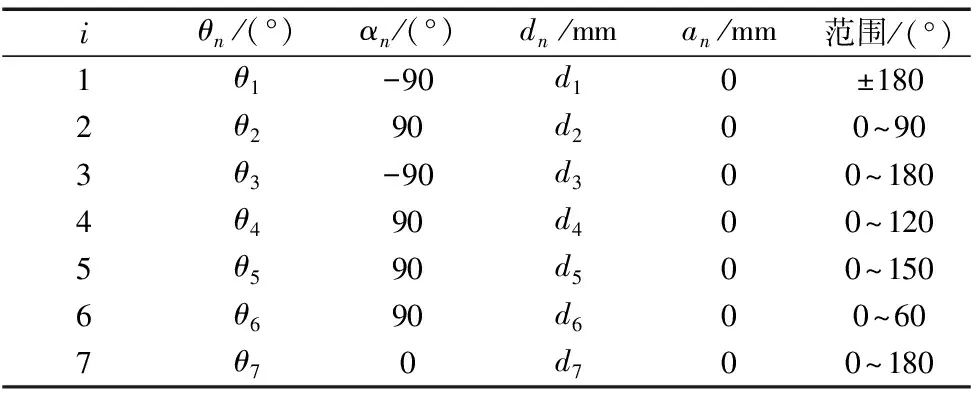
表1 7-DOF拟人机械臂D-H参数表

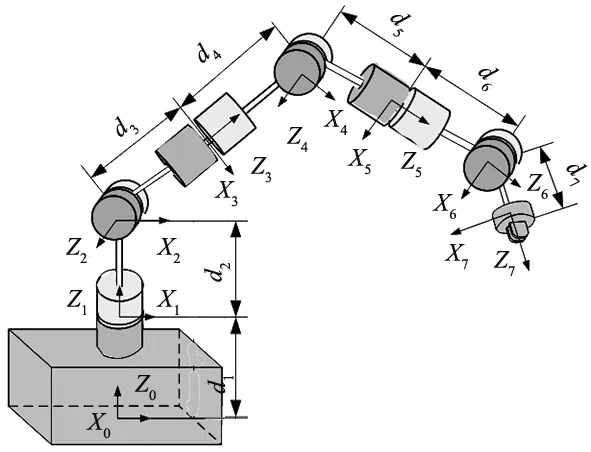
图2 7-DOF拟人机械臂连杆坐标系

齐次变换矩阵An描述第n坐标系相对于第(n-1)坐标系的位置和方位，

(1)

式中，Sθn=sin(θn),Cθn=cos(θn),n=1,2,…,7。

各连杆齐次变换矩阵相乘，得到J7坐标系相对于基坐标系的位姿齐次变换矩阵，即正运动学方程：

(2)

2.2 仿人机械臂运动学逆解

逆运动学求解是根据末端位姿0T7，求解θ=(θ1，θ2，θ3，θ4，θ5，θ6，θ7)的过程。图3表示的是仿人机械臂在工作过程中的任一姿态。肩关节S、肘关节E、腕关节W可以构成一个平面，定义为臂平面。J1的轴线方向BS、肩部S与腕部W方向SW构成一个平面，定义为参考平面。定义臂平面与参考平面之间的夹角为臂型角ψ。已知0T7时，S点、W点的位置以及向量SW的值是唯一的。仿人机械臂的自运动表现为肩关节S、肘关节E和腕关节W构成的平面绕SW运动。

图3 机械臂工作过程中的任一姿态

末端位姿0T7已知时，θ7不会影响到J6与J7原点的位置关系，通过0T7可以获得唯一的J6原点的位置，即：

(3)

式中，0P6为J6相对于基坐标系的位置向量。

同样的，θ2的变化不会影响A2与基坐标系B原点的位置关系，即：

(4)

式中,lBS为基坐标系原点到J2的连杆长度。

机械臂自运动不会影响肘关节E的大小，根据三角形余弦定理可以得到：

(5)

式中，lSE为J2到J4的连杆长度；lEW为J4到J6的连杆长度；lSW为J2到J6的空间长度。

机械臂关节J1～J3、J5～J7分别等效为肩部球关节S和腕部球关节W。根据冗余机械臂自运动特性[14]，给定ψ时，由于θ5～θ7不会改变E和W的位置，且θ4是一个连续变化的值，所以臂平面SEW的位置变化取决于θ1～θ3的变化。

当θ1=θ2=θ3=0°时，以S为原点建立初始机械臂肩部球关节S的坐标系Φso=(Xs，Ys，Zs，Os)，机械臂初始位置如图4a所示。

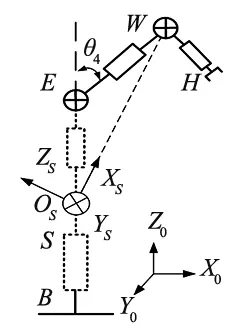
(a) θ1=θ2=θ3=0°时机械臂位姿

(b) θ1、θ2、θ3变化后机械臂位姿0T7

相对于基坐标系X0Y0Z0,Φso的三轴定义为：

BPW=[lEWsin(θ4)0lBS+lSE+lEWcos(θ4)],

BPS=[0 0lBS],Z0=[0 0 1]T

(6)

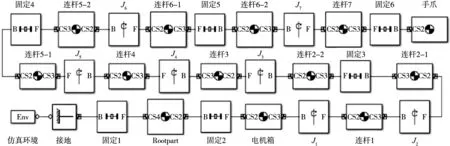
图6 SimMechanics七自由度仿人机械臂物理模型

式中,BPW是J6相对于基坐标系的位置向量；BPS是球关节S相对于基坐标系的初始位置向量。

J1～J3的角度由0°分别变化到θ1～θ3，臂型角则由0°变化到ψ，此时如图4b所示目标位姿下的机械臂肩部球关节S的坐标系为Φsd：

Φsd=Φso·Rot(XS,ψ)·ΦsoT

(7)

θ1～θ3构成球关节S的ZYZ欧拉角，其球形铰链变化公式为：

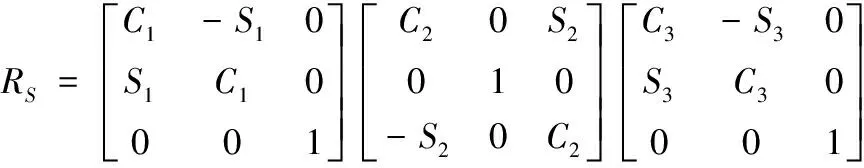
(8)

令Φsd(m,n)=Rs(m,n)，可求出θ1～θ3。

同样，θ5～θ7构成了球关节W的ZYZ欧拉角，其球形铰链变化公式：

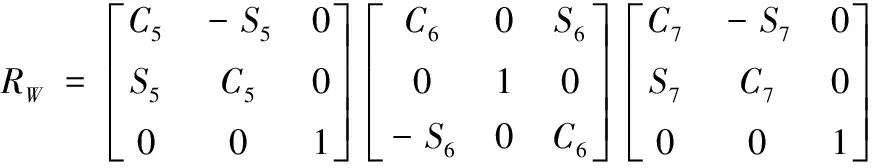
(9)

根据式(9)得到：

0R7=RSR4RW,RW=(RSR4)-1·0R7

(10)

令Rw(m,n)=((RsR4)-1·0R7)(m,n)，可求出θ5～θ7。

3 三维可视化运动学验证

作为Simulink的子模块，SimMechanics仿真平台建模简易方便，避免了推导运动学方程的繁琐，可以通过改变模型结构以优化系统参数，快速获取系统动态性能。如图5所示，在仿真软件中可通过虚拟现实工具箱直接观察到机械臂的运动画面。

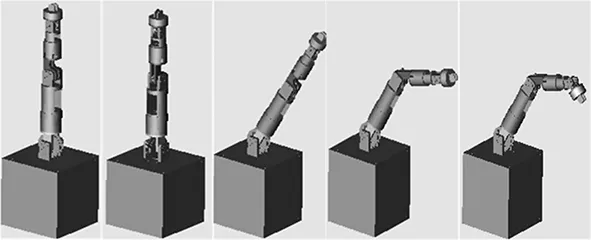
图5 机械臂运动画面

将机械臂三维模型导入SimMechanics，系统自动生成图6所示的机械臂物理模型。其中，仿真环境模块用于查看和修改机械臂模型的环境变量设置；接地模块表示惯性坐标系中一个相对地面静止的点，SimMechanics机构至少要有一个接地模块；固定模块表示两个物体之间没有自由度的关节，即两端物体之间没有相对运动；J表示物体之间的旋转关节模块，可以定义关节的运动速度、加速度、关节力矩等参数信息；连杆即Body模块，可以定义每个刚体质量、惯性矩张量等参数信息。

3.1 正运动学验证

在SimMechanics可视化仿真环境中，机械臂的初始位姿为其零位，各个关节、连杆坐标系设置与图2一致。选取图5中的5个末端臂型来验证机械臂正运动学方程的正确性，5组臂型下机械臂各个关节旋转变化角度以及末端位置如表2所示。

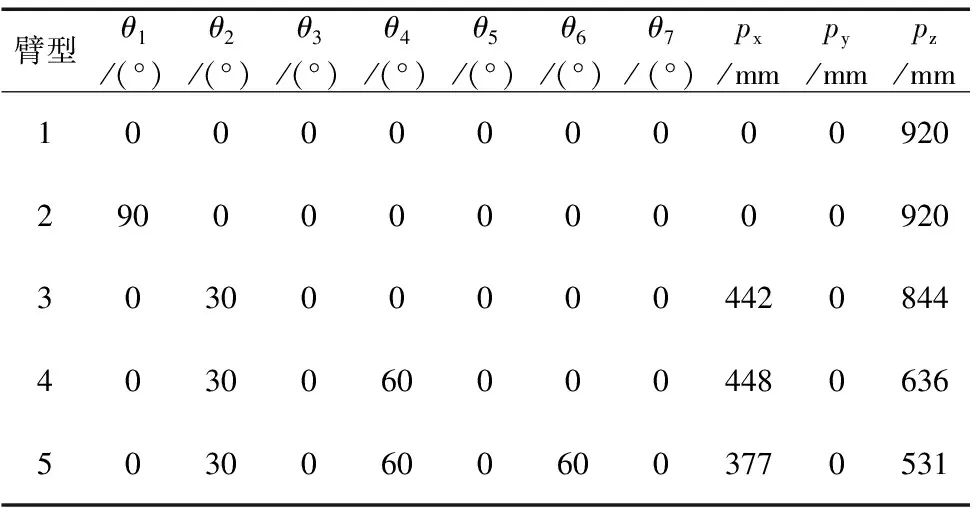
表2 正运动学5组臂型验证数据

可以看出：①各个关节角度均为0°，此时末端在基坐标系下的位置矢量为(0，0，920)；②θ1=90°，其余关节角均为0°，此时末端在基坐标系下的位置矢量为(0，0，920)；③θ2=30°，其余关节角均为0°，此时末端在基坐标系下的位置矢量为(442，0，884)；④θ2=30°，θ4=60°，其余关节角均为0°，此时末端在基坐标系下的位置矢量为(448，0，636)；⑤θ2=30°，θ4=60°，θ6=60°，其余关节角均为0°，此时末端在基坐标系下的位置矢量为(377，0，531)。图6所示的5组臂形与表2中的数据一一对应，从而验证了正运动学方程的正确性。

3.2 参数化运动学逆解验证

在不考虑机械臂关节限位的情况下，任意选取臂型角ψ=120°，给定末端位置0P7=[-40 160 180]。根据本文提出的逆解方法，结合给定末端位姿0T7与臂型角ψ，求出机械臂的8组逆解如表3所示。在SimMechanics环境中，将上述8组关节角θ输入到对应的关节驱动中去，得到如图7所示的8组逆解对应的机械臂位姿。可以看出，该8组位姿均相同，从而验证了逆运动学方程的正确性。

表3 指定末端位姿下的机械臂8组逆解 (°)

图7 运动学8组逆解验证

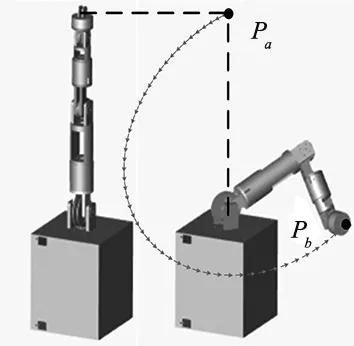
(a) 机械臂从零位Pa运动到指定末端位置Pb

(b) 机械臂运动路线

(c) 末端执行器在各方向上运动范围图8 机械臂从零位运动到指定末端位置

机械臂的实际运动控制需要对多组逆解进行筛选。可根据关节限位、碰撞干涉等因素排除部分解。当仍剩余多组可行解时，可按照机械臂运动过程中代价最小原则再次优选。综合考虑多因素并从中优选逆解，可提高机械臂作业的覆盖范围，并提高其障碍规避能力。

4 仿人机械臂工作空间分析

工作空间是衡量机械臂工作性能的依据之一，对机械臂的结构优化有着重要的意义[15]。蒙特卡洛方法是在机械臂各个关节运动范围内随机遍历取值，得到所有末端位置，组成其工作空间。

蒙特卡洛求解机械臂运动空间的步骤如下：

(1)根据正运动学方程，求出末端执行器相对于基坐标系的位置向量0P7=[pxpypz]；

(2)利用rand(j)函数，在各个关节运动范围取随机步长变量(θimax-θimin)rand(j)。有θi=θimin+(θimax-θimin)rand(j)，其中j=1,2,…,N；

(3)将(2)中的θi带入正运动学方程，求得末端执行器相对于基坐标系的位置向量。N的值越大，就越能反映机械臂的工作空间的准确性；

(4)用描点的方式将(3)中末端执行器的位置向量显示出来，形成机械臂的工作空间点云图。

取N=20 000，得到机械臂的工作空间点云图如图9所示。

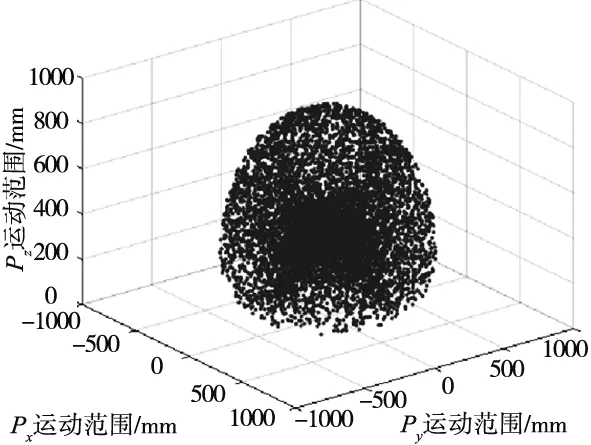
(a) 机械臂工作空间三维图

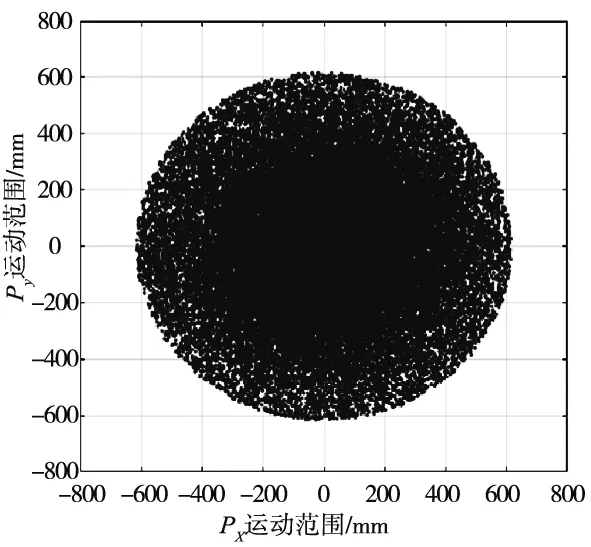
(b) XOY平面投影图

(c) XOZ平面投影图图9 机械臂工作空间点云图

由图9可知，机械臂工作空间形状紧凑，无明显空洞，类似于一个半椭圆球体,符合机械臂各个关节的实际运动空间，空间尺寸与机械臂的本体设计参数相对应。仿真结果与实际相符，从而验证了蒙特卡洛方法求解机械臂工作空间的正确性。

5 结论

以七自由度仿人机械臂为研究对象，采用D-H参数法建立了正运动学方程，根据仿人机械臂SRS结构特性定义臂平面、参考平面以及臂型角ψ，通过给定的末端位姿0T7以及ψ，快速求得了机械臂逆运动学8组解。在MATLAB-SimMechanics环境中，对机械臂正运动学5组数据、逆运动学8组解进行可视化验证，仿真结果表明了正、逆运动学方程的正确性。利用蒙特卡洛法分析机械臂的工作空间，结果准确直观。从而为后续的机械臂动力学分析、运动控制等进一步研究提供了参考依据。