群体机器人固定链路径形成算法*

韩 晓，雷 斌

(武汉科技大学 a.机械传动与制造工程湖北省重点实验室；b.机器人与智能系统研究院，武汉 430081)

0 引言

群体机器人路径形成算法是由群体机器人觅食任务[1]发展而来。由于其运用分布式控制而且对单个个体能力要求较低等特点，近些年来，被国内外广泛学者关注。路径形成[2]算法指的是一种过程，在该过程中，机器人能够在同一个环境中的两个目标位置之间构建一条路径，从而使一个位置到另一个位置所需时间最小化。这个过程根据两个目标位置之间的路径是由固定机器人链标记还是由沿该路径移动的连续机器人维持来进行区分。同时路径形成算法强调机器人之间仅仅需要进行局部通信便能完成一个任务。整个算法的复杂度不会随着机器人数量上升而上升。所以该算法被大量用于未知环境探索、排雷，路径优化等任务。同时该算法被认为在未来发展中十分有潜力的[3]。然而目前这些算法的模型很多参数过于理想化，大都是利用一个集中式的控制方式。利用全局信息对每个机器人进行控制[4]，在这样的算法下，随着机器人数量的增加[5]，整个系统的控制复杂度会变得非常大。

有一些研究机构意识到了这个问题，并且开始针对一些分布式算法做一定的研究[6]。如哈佛大学的群体机器人研究小组针对固定链的路径形成算法提出了一种基数算法[7]，并在机器人仿真软件中进行了实验，但最终没有在同类算法中做出相应对比，无法得知该分布式算法的真实效率。还有一个通过无分支的机器人链进行路径形成算法研究[8]。算法中默认在机器人链中无法从中间生成新的链，这样的算法也是十分局限的，并且算法的效率也无法被评估。这些理论大部分只考虑了固定链路径形成算法中的某些策略，没有对多种固定链路径形成算法进行比较，最终也无法比较算法内不同规则的优劣。无法验证不同路径形成算法的优势，也就无法在对应的场景使用更加合适的路径形成算法。

本文描述了两种固定链路径形成算法。并通过改变初始释放条件从而研究这两种算法的机器人搜索效率。为了更加全面的描述这两种算法的优劣，通过设置障碍物，在有障碍物情况下探索了两种算法的搜索效率。

1 基于固定链的路径形成算法

基于固定链的路径形成算法主要分为有支链(图1)和无支链(图2)两种，该算法能够利用一些机器人的局部通信交互，连接未知区域中两个特定位置之间的路径。与传统的蚁群算法[9]不同，机器人不需要对环境进行标记，有较好的鲁棒性。机器人通过与环境和其他机器人之间的局部信息交互实现对前进方向的选择。同时机器人将根据其他机器人的信号转换自身的状态。通过前进方向的概率选择模型和自身的状态转换模型。最终搭建一条完整的路径。

图1 有支链的路径形成算法

图2 无支链的路径形成算法

1.1 路径形成算法选择概率

路径形成算法选择概率模型是基于随机游走模型[10]，游走机器人从起始点开始后向四周进行不规则运动，接近于布朗运动。游走机器人在每一次游走过程中，随机选择要到的节点，并以该节点作为下一次运动的起始点，该过程不断重复。

设对于每一只蚂蚁而言，他们随时间的每一步位置为Xi,下标为0，1，2…,Xi的取值集合称为该过程的状态空间S，该组变量具有马尔科夫性质[11]，即下一步状态只取决于当前状态，与之前状态无关，如下公式所示：

P(Xn+1=x|X1=x1,X2=x2,…,Xn=xn)=

P(Xn+1=x|Xn=xn)

(1)

式中，P(Xn+1=j|Xn=i)被称为转移概率pij,表示在第n步位置在i的状态下，第n+1步在位置j的概率。同时转移概率满足正定性和有限性的约束，即当前点向下一目标点转移概率要在0～1之间，并且当前点向周围所有能够转移的点的移动概率总和为1。

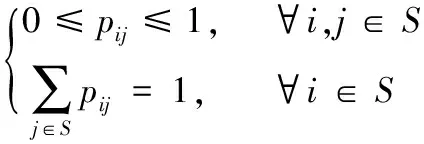
(2)

假设在一张地图上一共有n个能够停留的节点和m条节点与节点之间的通道。组成的图G(V,E),V代表了n个节点的节点集合，E代表m个通道的节点集，节点v的度记为d(v)，即该节点对应的分支数量。所有的游走机器人从V0出发，在整张图上做随机游走和避障运动。机器人行走到第t步时，机器人处在Vt位置，下一步，到达Vt任意的相邻且无障碍物的节点的概率相同，为1/d(vt)。同时有加权图e(vi,vj)上存在权重w，W={w1,w2,…,wk,…}表示加权集。

d(vi)=∑e(vi,vj)∈Ew(vi,vj)=∑vj∈Vwij

(3)

(4)

从节点i到节点j的状态转移概率等于节点i到节点j转移的权重除以节点i的度。而马尔可夫状态转移矩阵M=(pij)i,j∈V。于是对于整张地图，设Pt(X=xi)表示在第t步状态下在节点xi处的概率。Pt(X)表示第t步的概率分布向量。则有以下递推公式：

Pt+1=PtM

(5)

1.2 路径形成算法状态转换规则

在固定链路径形成算法中，机器人从巢穴出发，并且机器人自身有两种状态，一种是随机游走和避障的“探索者”状态，还有一种是在碰到食物后固定不动，从而引导其他机器人的“引导者”。

“探索者”：所有机器人在从巢穴出发时均为探索者状态，机器人采取随机游走算法，同时对周围的障碍物以及机器人采取避障策略。当“探索者”在自己的通信范围内找到了食物或者是其他“引导者”，自身转变状态成为“引导者”，并且停在原地。

“引导者”：当“探索者”在自己感知范围内发现了食物，或是其他“引导者”，自身变为“引导者”，并停止运动。

1.3 有无支链的路径形成算法规则

(1)有支链的路径形成算法，强调“搜索者”能够在“引导者”的任意节点变成“引导者”，从而变成链上的一个新的节点。每个节点自身有一个数字信息，用O来表示，O表征了该节点距离食物的距离，O值越大代表离食物越远。为了使这种觅食链更快地收敛，定义了如下公式：

Oj=min{Oi}+1(i∈Rj)

(6)

其中，Oi表示第i个机器人的O值，Rj代表了第j个机器人的接受范围，图中虚线部分表示的是每个机器人的接受范围。当机器人成为“引导者”时，机器人自身的O值符合上述公式。以该机器人通信范围内O值最小的一个机器人为基础，加上1，作为自身的O值。这样的策略能够保证多链聚集的时候，末端的节点O值总能够保证较小。从而找到一条从食物到巢穴相对近的路径。

(2)无支链的路径形成算法，考虑到有支链的路径形成算法对机器人数量要求较高，设计了一种无支链的固定链路径形成算法。该算法中，对“探索者”多了一层约束。当机器人进入“探索者”状态时，仅仅在感知到食物或末端的“引导者”时才改变自身状态为“引导者”。“搜索者”不能在已经形成的觅食链的非末端节点改变自身状态。

2 仿真的设置与实验

本文采用栅格法对环境进行地图建模[12]。利用栅格将二维地图划分为一个个网格单元，在仿真环境中设置了一个10×10格的地图，蚂蚁机器人每次能够行走一个格子的步长。设置地图的左下角为巢穴，所有蚂蚁机器人从巢穴出发，整个地图的右上角是食物。机器人有两种状态，一种是作为随机游走的“探索者”机器人，另一种是找到了食物或食物链的“引导者”机器人。机器人之间的释放间隔为t,设置单位时间所有机器人移动一个步长。当第一条从食物到巢穴的完整链形成后，路径形成任务被认为完成。机器人形成的固定链子长度，用L表示。

每个处于“探索者”状态的机器人，在环境中会出现图3中的5种情况。图中的叉标志表示在该方位上有出现障碍物或者是其他机器人。

图3 “探索者”机器人前进方向选择

当机器人四周无任何障碍物或者其他机器人时。机器人的4个方向作为概率选择的目标区域。机器人严格遵循概率选择公式。即在当前点下对4个方向均为1/4的选择概率。

当机器人周围有1～3个障碍物或其他机器人时，机器人前进的概率选择区域变成了3～1个目标区域。即对应机器人当前节点的度d(v)为3～1。当机器人四周无可行走区域，机器人原地保持静止，持续一个步长的时间。机器人运行流程图见图4。

图4 机器人运行流程图

本仿真采用联想Y7000p笔记本进行仿真实验，CPU为i7-10875,16GB内存，在Windows10操作系统下，利用VS2019进行仿真。在命令行下利用C语言实现仿真，C语言具备极高的效率，保证仿真能够稳定高效的进行。

如图5所示，设定释放时间间隔为15，程序中，障碍物用黑色矩形表示，机器人处于“搜索者”状态时用红色五角星表示，食物用蓝色椭圆表示，巢穴默认在左下角，用黄色椭圆表示。在有支链的路径形成仿真中，“引导者”用绿色五角星表示，在无支链的路径形成算法中，作为链上末端节点的引导者用蓝色五角星表示，作为链上的非末端节点用绿色五角星表示。地图中空白部分表示当前位置没有任何机器人。以机器人释放时间间隔为变量，仿真了t从5～90之间的85种情况。绘制出了机器人完成任务步数关于t的变化曲线。如图6、图7所示。

图5 t从50～400程序仿真图

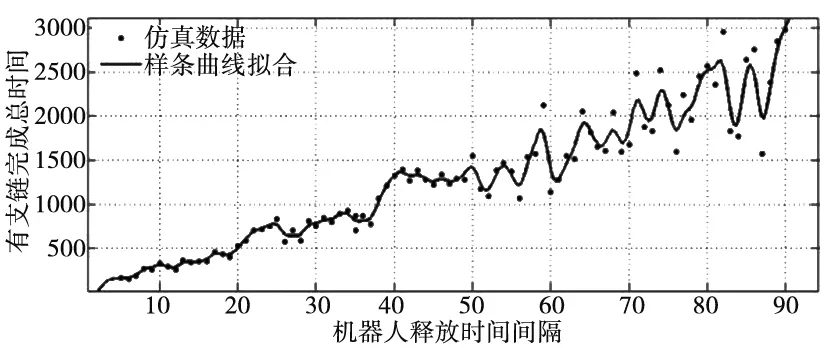
图6 有支链路径形成算法

图7 无支链路径形成算法

可以看出两种路径形成算法中，搜索路径用到的总时间，都随着机器人释放时间间隔的增加而增加。同时在t=50之后，两个算法的随机性开始变大，针对单链的路径形成算法，在t=50之后，完成任务的时间，随着t的变化随机性远大于多链路径形成算法，说明在t较长时，多链的路径形成算法，较为稳定。

进一步定义整个路径形成算法的效率为最终使用机器人总数和找到路径的最短时间的乘积[13]。

由图8、图9可得，路径形成算法的搜索效率会随着机器人释放时间时间间隔的增加而下降，同时在机器人释放时间间隔较短的时候，效率的波动较大，与完成时长相反。对无支链链路径形成算法来说，搜索效率刚开始随时间间隔变大下降的较快，但很快效率较低到一定数值变保持稳定。而多链路径形成算法，刚开始效率下降的较慢，并且随着机器人释放时间间隔的不断增加，效率还在持续下降。说明，在机器人释放间隔时间较短的情况下，多链路径形成算法的效率要明显优于单链路径形成算法，但当释放时间间隔较长时，单链的路径形成算法会更优，能够在较长一段时间内保持稳定。

图8 有支链路径形成算法效率

图9 无支链路径形成算法效率

3 有障碍物情况下路径形成算法效率

为了更加全面的比较两种算法之间的差异，在环境中人为加入了一定的障碍物，设置了一种障碍物的情景，如图10所示，在巢穴和食物之间设置了障碍物。机器人需要通过更为弯曲的复杂路径才能找到食物。在这样的实验环境下，分别对两种算法进行了仿真。图中，右上角蓝色椭圆表示食物，左下角黄色圆圈表示巢穴，图中绿色五角星表示“引导者”身份的蚂蚁，红色五角星表示“探索者”身份的蚂蚁，蓝色五角星代表固定链的末端“引导者”身份的蚂蚁。图中的障碍物用黑色矩形表示。

图10 带障碍物的地图

针对这两种有障碍物的地图，绘制了释放时间间隔t的变化带来的机器人探索效率的变化图。如图11～图14所示。根据和第二章的对比发现，针对完成时间这个指标，两种算法在有无障碍物地图中表现的整体趋势一样。在有障碍物的地图中，两种算法用的总时间都有一定程度的增加。针对无支链路径形成算法，由于障碍物的加入，算法在释放时间间隔大于60后，随机性开始增大。相比无障碍物来说延后10个释放时间间隔。说明针对更加复杂的地形，地图中的障碍物可以让无支链路径形成算法跟稳定，允许机器人释放时间更长。

图11 有障碍物有支链路径形成算法

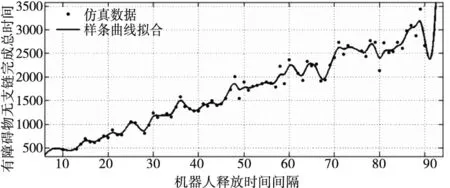
图12 有障碍物无支链路径形成算法

图13 有障碍物有支链路径形成算法效率

图14 有障碍物无支链路径形成算法效率

对于时间间隔在5～90之间，路径形成算法在机器人施放时间间隔较短时，算法效率波动较大。算法效率在40～60之间较为稳定，将这个区间内的数据作为研究对象，得到表格如表1所示。

表1 算法效率对比

可以看出，在环境中移除障碍物，无支链路径形成算法提升效率远远高于有支链路径形成算法。说明在没有障碍物的情况下，无支链路径形成算法效率会略高于有支链的路径形成算法，但当环境中出现了一定的障碍物，无支链路径形成算法效率会较快的下降，有支链路径形成算法对于有障碍物的环境适应性较好。

4 总结

本文针对路径形成算法目前的研究过于理想化、缺乏相关理论公式，和缺乏自我对比等问题提出了有支链和无支链两种路径形成算法。有支链路径形成算法在机器人施放时间间隔较长的前提下，对有障碍物的环境适应性更好。而无支链路径形成算法在无障碍环境中整体稳定性会更优。实验结果表明两种算法各有优劣，需根据不同场景中障碍物情况和机器人的释放间隔等约束选用合适的算法。