特定五维载荷工况下滚动直线导轨副载荷分布研究*
叶坤奇,周长光,冯虎田,王晓艺
(南京理工大学机械工程学院,南京 210094)
0 引言
滚动直线导轨副作为数控机床的关键功能部件,其刚性直接影响主机的加工精度和稳定性,因此刚性成为滚动直线导轨副极其重要的性能指标[1]。在其工作过程中,滚珠和滚道的接触状态是决定其刚性的关键因素,但由于其结构的复杂性,很难直接检测到其内部滚珠的力学行为。因此,建立其力学模型实现接触状态的精确数值计算对研究滚动直线导轨副的刚性具有重要意义。
在立式升降机床或存在偏心载荷的设备中,滚动直线导轨副在工作过程中会出现承受惯性力偏载和切削力等载荷不均的情况,导致滑块受到五维载荷的作用[2],五维载荷会直接改变滚动直线导轨副的载荷分布,影响滚珠-滚道的接触状态,进而改变导轨副的刚性和稳定性。国内外许多学者对滚动直线导轨副的负载接触模型进行了研究:文献[3-4]研究了偏心载荷下滚动直线导轨副在空间五维的动态行为;Hiroyuki Ohta等[5-6]建立了滚动直线导轨副力学模型,分析了滚珠俯仰,旋转,偏航,垂直和水平等五维运动行为;文献[7-9]建立空间五维刚度模型,得到了垂直方向和水平横向以及绕3个空间轴的偏转角,并最终求得了导轨副五个维度下的刚度;刘建素等[10]对比了两种典型的滚动直线导轨副分别在五维载荷作用下的变形;文献[11-12]建立了导轨副滚珠和滚道接触表面载荷平衡方程,得出了每个滚珠轴向和径向位移以及俯仰、偏航和振动方向的偏转角;
但通过上述研究内容发现,在针对滚动直线导轨副受空间五维载荷作用下的载荷分布和动态特性研究中,鲜有考虑滚珠精度误差对载荷分布的影响研究。Wang W等[13]分析了具有随机几何参数滚动直线导轨副的运动精度和可靠性,计算了考虑随机几何误差下的动态矩。在滚珠丝杠副研究领域,有很多相关研究可以借鉴:Zhen N等[14]将随机几何误差细化到滚珠精度误差,对滚珠丝杠副进行力学分析,通过Newton-Raphson数值迭代计算得到每一颗滚珠的接触载荷;Zhao J J等[15]提出了考虑几何误差并受装配误差引起的力矩影响的滚珠丝杠副载荷分布模型;
由此可见,目前尚缺少同时考虑特定五维载荷和滚珠精度误差工况下的滚动直线导轨副载荷分布研究,本文建立了特定五维载荷工况下滚动直线导轨副的载荷分布模型,并运用Newton-Raphson数值迭代计算方法求解此模型中所有滚珠的接触载荷。以一款滚动直线导轨副为例,利用有限元仿真验证了载荷分布模型的准确性。分析本文理论模型的计算结果,进一步研究了特定五维载荷工况对滚动直线导轨副载荷分布的影响。
1 滚动直线导轨副载荷分布模型
如图1所示,建立滚动直线导轨副的空间直角坐标系,图中:{o,x,y,z}为导轨副的固定坐标系,{o1,x1,y1,z1}为滑块的移动坐标系,原点o和o1为滑块几何中心。基于滚动直线导轨副的结构特点,其沟槽内部多排滚珠均匀分布,依据滑块的位置形成了导轨副动结合面,从而对滑块在其他5个方向上的运动产生约束[16]。工作过程中,工作台及相应工件安装在滑块之后,滑块和导轨进行相对运动,理想状态下,所有部件均为理想刚性体,移动部件沿导轨方向直线往复运动,移动坐标系{o1,x1,y1,z1}的坐标轴始终平行于固定坐标系{o,x,y,z}。然而,在某些特定工况下,由于工作台的受载不均或其他工作载荷的作用,导致滑块会在空间产生扭转运动,本章将此运动行为在空间上分解为受x,y,z方向力矩Mx,My,Mz作用的扭转运动分别进行分析;同时,滚珠存在精度误差,误差导致滑块在沿导轨方向和其他5个方向上的动态行为产生波动[16]。
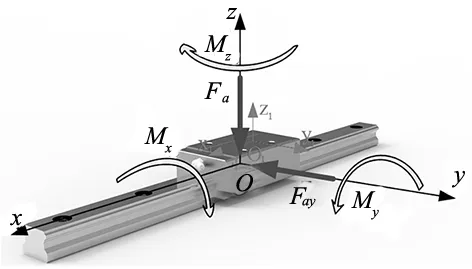
图1 滑块所受各个方向力矩示意图
根据Hertz接触理论,每颗滚珠接触载荷与接触变形的关系可以表示为[17]:
(1)
式中,δij代表第j排第i颗滚珠受力矩作用后的法向接触变形量;Psij代表滚珠法向接触载荷;μ代表赫兹接触系数;∑ρ代表接触点处主曲率和;E1、E2、v1、v2分别代表滚珠滚道的弹性模量和泊松比。
将式(1)简记为:
(2)
其中,系数:
(3)
根据文献[17]计算得到,赫兹接触系数μ=0.627 3,导轨副主曲率和∑ρ=0.51 mm-1,从而得出系数K=6.02×105。
本文在建立滚动直线导轨副载荷分布模型的过程中作出以下假设:
(1)滑块轴的倾斜角度为正值;
(2)当滑块根据图2所示的导轨轴顺时针倾斜时,滑块表面的外部力矩在整个导轨副行程中恒定;
(3)运动过程中的倾斜角恒定;
(4)不考虑整个滚动直线导轨副固定方式引起的线性安装误差。
1.1 考虑滚动体精度误差的滚转载荷分布模型
不考虑预紧的情况下,受Mx作用下滚动直线导轨副的载荷关系如图2所示。滚珠与导轨滚道和滑块滚道之间的接触变形是由竖直方向载荷Fa和力矩Mx引起的。θ′为导轨轴和滑块轴之间的倾斜角。沿x负方向定义左上方为第1排滚珠,顺时针依次为第2、3、4排滚珠。图3为第2排滚珠变形后接触角αij示意图。

图2 Mx作用时导轨副载荷关系
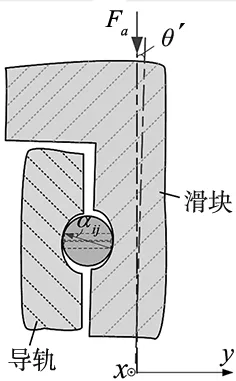
图3 第2排滚珠接触角放大图
基于图2和图3,垂直纸面向外为x正方向,y方向如图所示。则载荷平衡方程可以写成:
Fa=2z·Psncosαij·cosθ′
(4)
其中,z为每排实际承受载荷的滚珠数,只有1、3排滚珠实际承载,且每颗受载滚珠的接触载荷相同,大小为Psn,受Mx作用时,每颗受载滚珠变形后的接触角均为∂ij,θ′为x方向力矩作用下的滑块偏转角[1,18]。
(5)
其中,δi3为第3排第i颗滚珠受力矩作用后的法向变形量,S2为1、3排滚珠中心距,α0为初始接触角,α1为第1、3排滚珠中心连线与水平线夹角。
如图2所示,力臂S1可以表示为:
(6)
其中,Lx为第1、2排滚珠中心距。滚动直线导轨副受Mx作用时,有如下平衡关系:
Mx=z·Psn·S1
(7)
当外部力矩作用于滚动直线导轨副上时,滚转轴可被视为与导轨轴一致。图4为滚珠中心和导轨、滑块滚道中心在法线部分的相对位置。假设滚珠中心O0与导轨滚道中心Or和滑块滚道中心Oc位于同一条直线上;滚珠与滚道之间的接触点为E、F;则导轨滚道中心Or到滑块滚道中心Oc的距离可以写成:
D=OrOc=rr+rc-db
(8)
其中,rr、rc和db分别是导轨滚道曲率半径、滑块滚道曲率半径和滚珠直径。
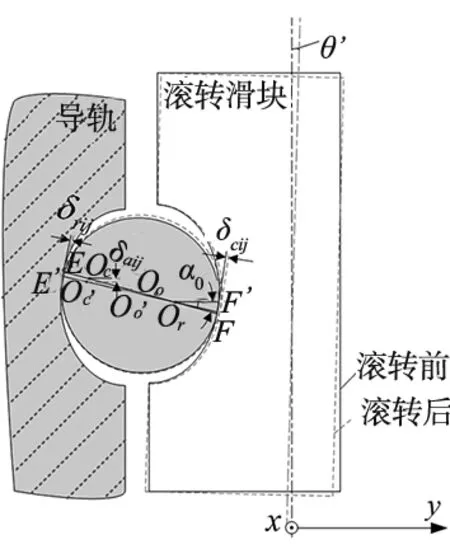
图4 滚珠中心与滚道中心的相对位置
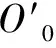
(9)
其中,R′为滑块滚道中心的滚转半径,有以下关系:
(10)
其中,dm为滑块宽度;滚动直线导轨副的接触变形由导轨接触变形δrij和滑块接触变形δcij组成,第j排第i颗滚珠的法向接触变形可以表示为:
(11)
若考虑滚珠的精度误差,则滚珠的法向接触变形为:
(12)
其中,Eij为任意滚珠的随机精度误差。基于图4的几何关系,滚珠变形后的径向位移可以表示为[11](假设受Mx作用时滚动直线导轨副每排滚珠变形量相同):
(13)
滚珠变形后的接触角:
(14)
若考虑每颗滚珠的精度误差,则滚珠变形后的接触角为:
(15)
综上所述,Mx单独作用时,考虑滚珠精度误差的滚珠滚转载荷模型为:
(16)
(17)
1.2 考虑滚动体精度误差的俯仰载荷分布模型
不考虑预紧的情况下,受My和Mz作用下导轨副负载情况分别如图5、图8所示。
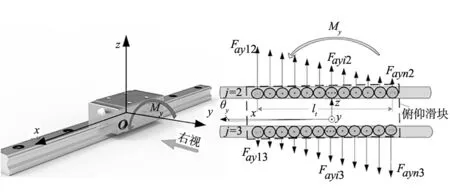
图5 My作用时导轨副载荷关系
第2、3排滚珠的载荷分布情况如图5所示。在力矩My作用下,上下排滚珠的受力情况相反,第2排第1颗滚珠受载荷Fay12为最大,则第3排第1颗滚珠受载荷Fay13为最小。由于上下排滚珠的载荷分布相反,所以仅分析第2排滚珠的受力情况即可,Fayi为滚珠i的工作载荷,则有:
(18)
其中,Fay为受My作用下第2排滚珠的工作载荷。每颗滚珠的竖直工作载荷与其法向接触载荷有如下关系:
Fayij=Psijcosα0
(19)
其中,Fayij为每颗滚珠受My作用下滚珠的竖直工作载荷,Psij为每颗滚珠受My作用下的法向接触载荷。
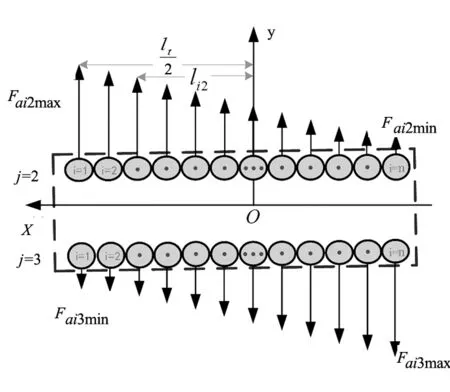
图6 My作用下滚珠力臂
图6为y方向力矩作用时2、3排滚珠力臂示意图,其中lt为每排滚珠有效承载长度。基于图6,力臂lyi可以表示为:
(20)
图7表示受My作用前后第2排滚珠几何关系。
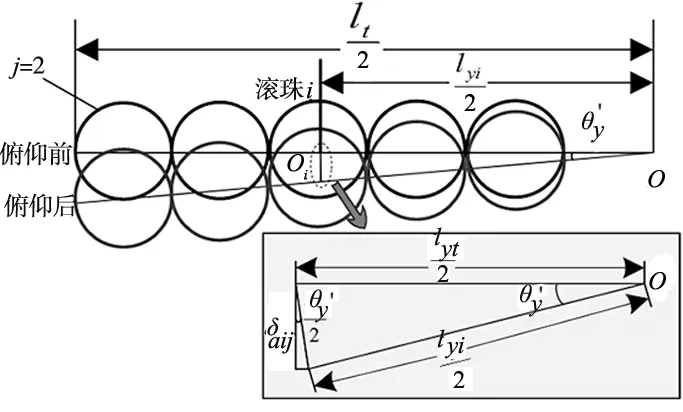
图7 My作用下第2排滚珠几何关系
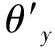
(21)
由公式(13),每颗滚珠的法向变形量δij为:
(22)
因此,受My作用时,导轨副受载平衡方程为:
(23)
若考虑滚珠精度误差,则有:
(24)
在这种情况下:
(25)
(26)
则考虑滚珠精度误差情况下受My作用的受载平衡方程为:
(27)
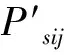
综上所述,My单独作用时,考虑滚珠精度误差的俯仰载荷分布模型为:
(28)
(29)
1.3 考虑滚动体精度误差的偏航载荷分布模型
同理,在力矩Mz作用下,左右两排滚珠受力情况相反,第1、4排,第2、3排滚珠载荷分布分别相同,载荷分布如图8所示。可以看出,力矩Mz作用下的滚珠受力情况与力矩My作用下的情况相似,故其受载平衡关系为:
综上所述,Mz单独作用时,考虑滚珠精度误差的滚珠偏航载荷分布模型为:
(30)
(31)
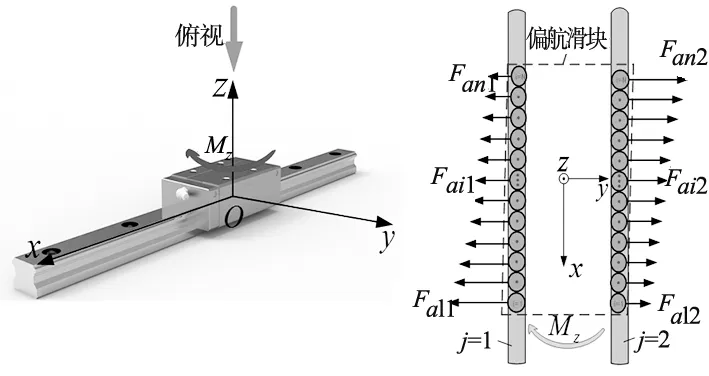
图8 Mz作用时导轨副载荷关系
2 数值计算分析
为了验证本研究中理论模型的准确性,本文利用Ansys Workbench19.0创建了滚动直线导轨副静力学3D仿真模型,仿真所用导轨副为THK公司SHS-25V型号滚动直线导轨副,其参数如表1所示。
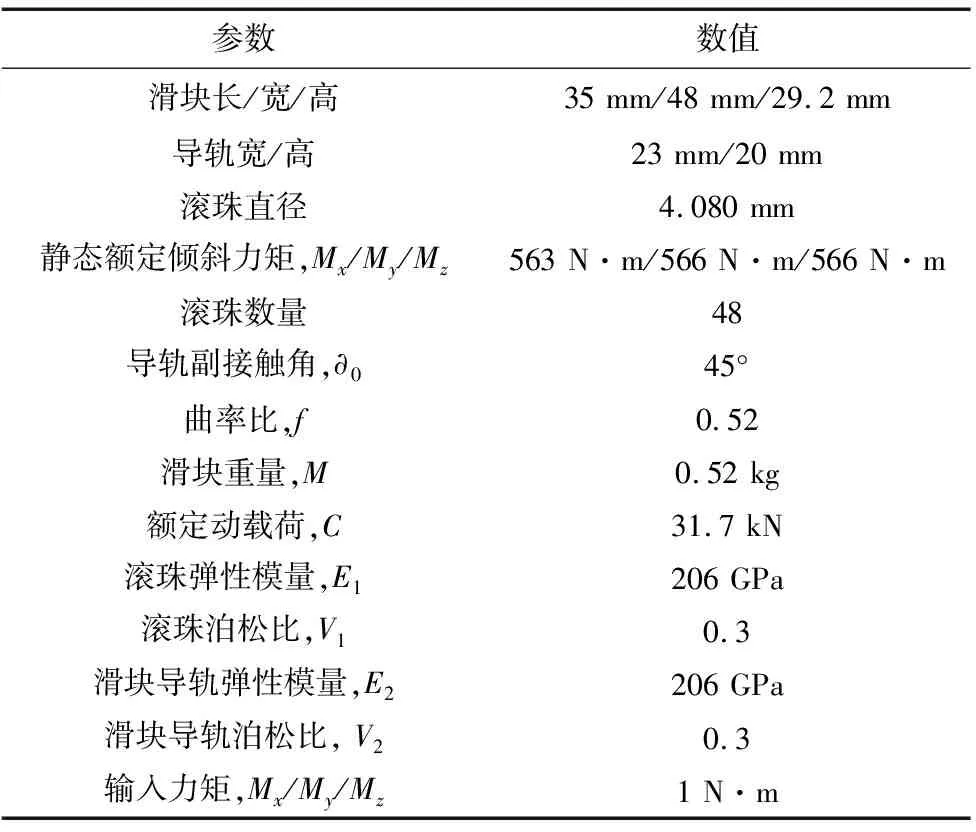
表1 滚动直线导轨副参数
2.1 仿真结果
图9为载荷作用下SHS-25V滚动直线导轨副所有滚珠的应力应变云图:导轨副受Mx作用时,第1排和第3排滚珠受载较大,同排滚珠的应力分布较均匀;受My作用时第1排和第2排、第3排和第4排滚珠应力应变情况相似,上下排滚珠的应力应变情况相反;受Mz作用时第1排和第4排、第2排和第3排滚珠受力情况相似,左右排滚珠的应力应变情况相反。这与图2、图5以及图8中的理论分析相符。

(a) 受X方向弯矩时应力 (b) 受X方向弯矩时应变

(c) 受y方向弯矩时应力 (d) 受y方向弯矩时应变
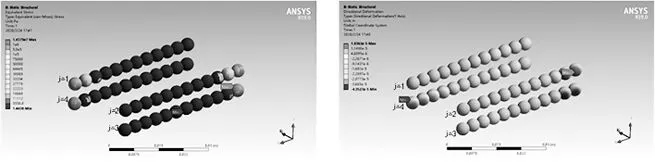
(e) 受z方向弯矩时应力 (f) 受z方向弯矩时应变
为了验证文中滚动直线导轨副载荷分布模型的准确性,图10~图12列出了本文及有限元仿真计算得出的3种力矩分别作用时每一颗滚珠的法向接触载荷。
由Ansys仿真结果可知,导轨副受大小为1 Nm的Mx作用时每排滚珠受力均匀,并且只有第1、3排滚珠有明显载荷,理论计算与仿真结果中滚珠接触载荷最大误差为0.231 N;导轨副受My作用时上下两排滚珠受载分别减小和增大,理论与仿真结果最大误差为0.232 N;导轨副受Mz作用时左右两排滚珠受载分别减小和增大,理论与仿真结果最大误差为0.145 N。Ansys Workbench模型求解的滚珠载荷分布结果与本文理论模型最大误差为9.13%,验证了本文建立的滚动直线导轨副载荷分布理论模型的准确性。
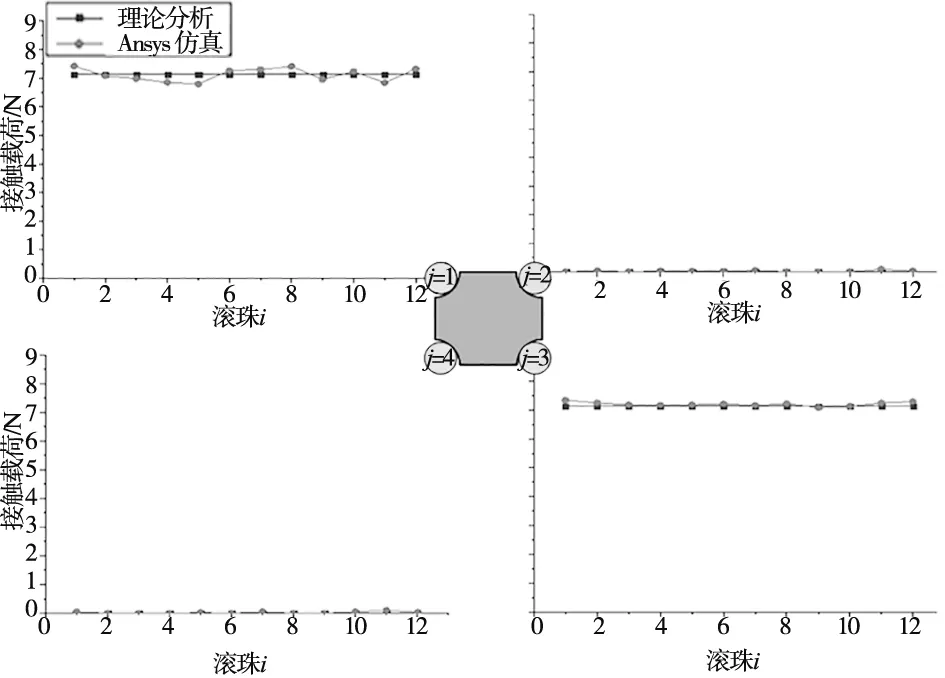
图10 Mx作用时理论与仿真结果
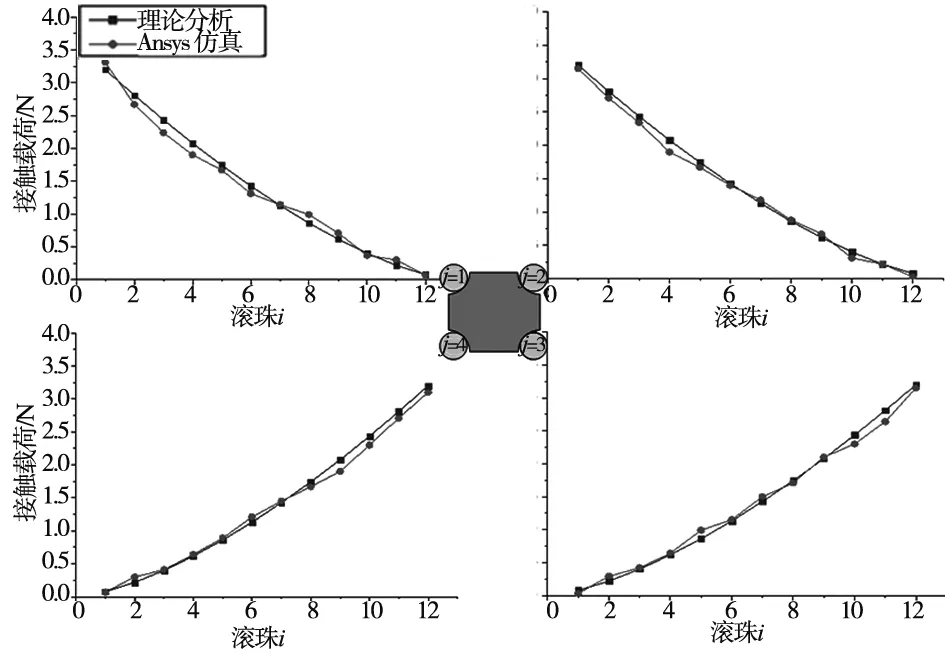
图11 My作用时理论与仿真结果
2.2 结果分析与讨论
2.2.1 力矩大小对载荷分布的影响
当工作载荷为1 kN的情况下,力矩大小对导轨副滚珠载荷分布影响如图13~图15所示。由图13~图15可知:当工作载荷为1 kN时,三个方向滚珠载荷分布均随力矩增大而增大;受Mx作用时,第1、3排滚珠受载明显,而第2、4排滚珠几乎无载荷;受My和Mz作用时,力矩越大,滚珠载荷分布越不均匀。

图13 工作载荷为1 kN时Mx对滚珠载荷分布的影响
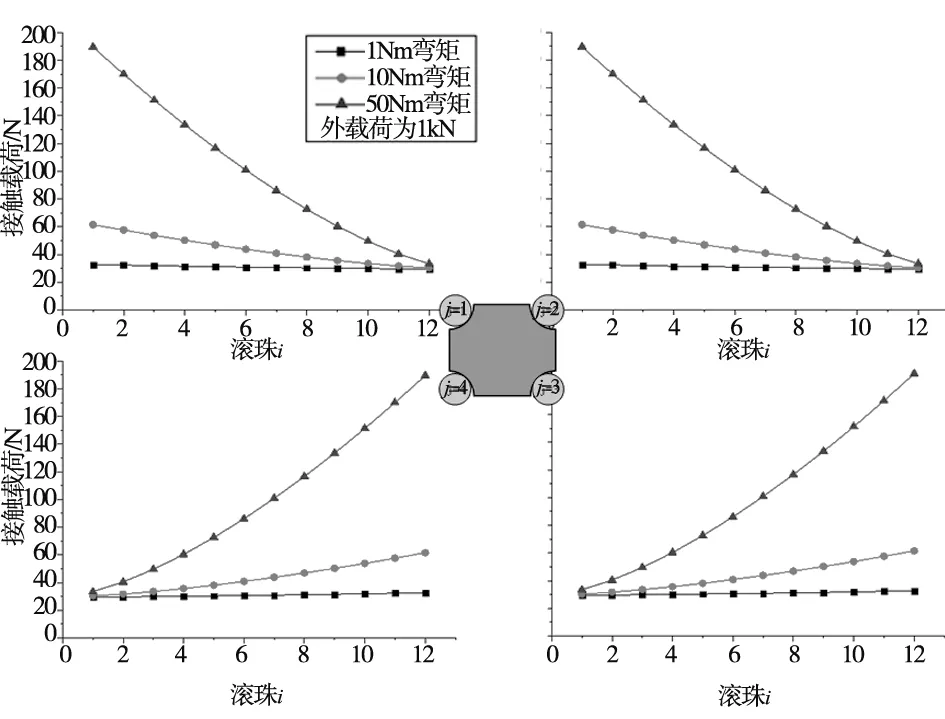
图14 工作载荷为1 kN时My对滚珠载荷分布的影响
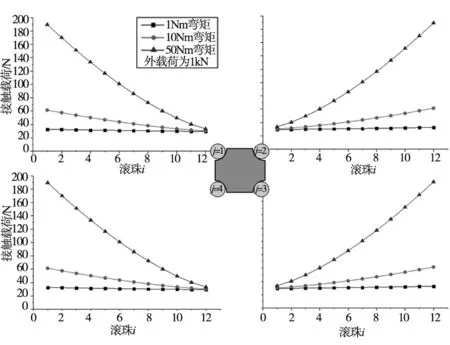
图15 工作载荷为1 kN时Mz对滚珠载荷分布的影响
2.2.2 滚珠精度误差对载荷分布的影响
设置工作载荷为1 kN,各方向力矩为10 Nm,在MATLAB仿真中随机产生误差范围为±1 μm和±2 μm,考虑滚珠精度误差Eij及力矩的情况,滚动直线导轨副载荷分布情况如图16~图18所示。由图16~图18可知:在空间五维载荷作用下,精度误差会导致载荷分布波动变大。可见,精度误差会使导轨副载荷分布产生波动,且误差越大,波动越大,载荷分布越不均匀。
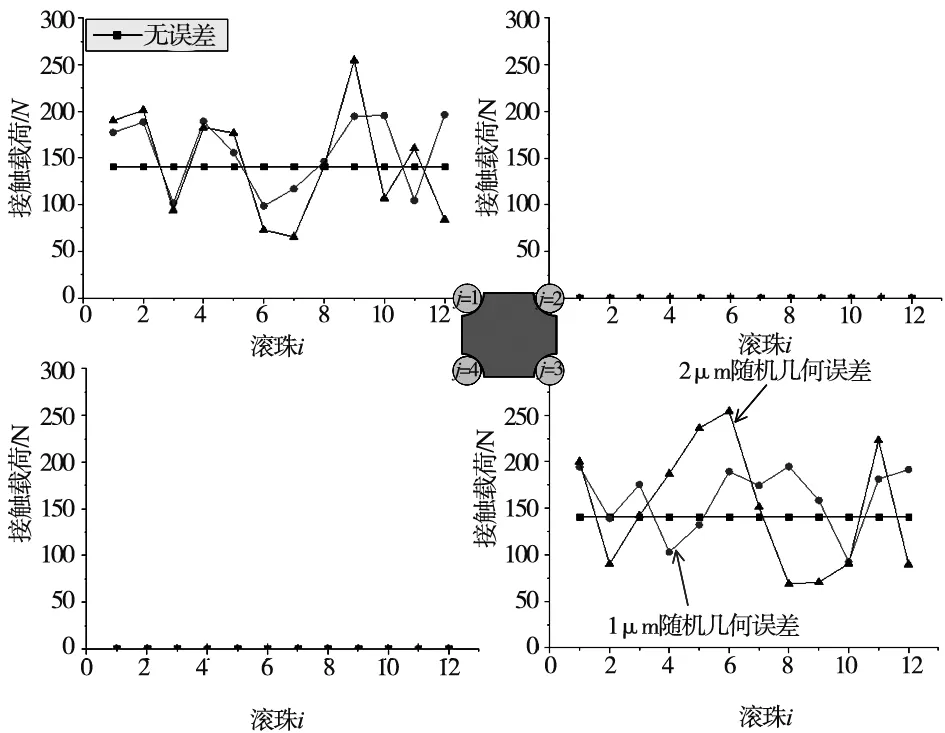
图16 作用时滚珠精度误差对滚珠载荷分布的影响
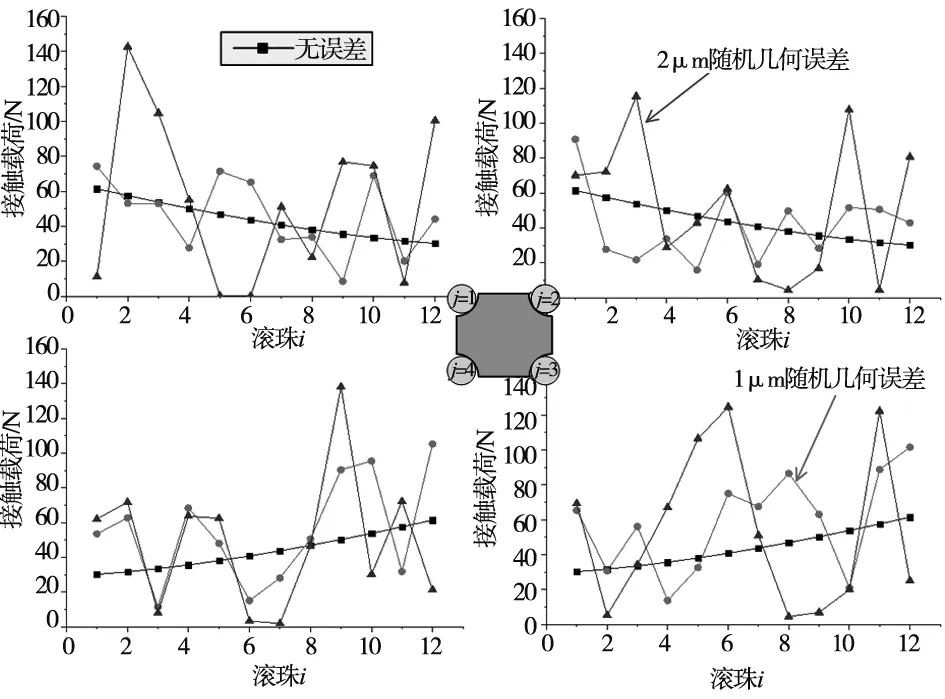
图17 My作用时滚珠精度误差对滚珠载荷分布的影响

图18 Mz作用时滚珠精度误差对滚珠载荷分布的影响
3 结论
本文重点研究了考虑特定五维载荷工况的滚动直线导轨副载荷分布模型。综合动力学分析和仿真分析结果最终得出:
(1)导轨副受五维载荷作用时,对滚珠的载荷分布会才生较大的影响。例如本文分析受Mx作用时,1,3排滚珠承受载荷而2,4排滚珠不受载;受作用时,第1排第1颗滚珠接触载荷比第12颗大93.42%。因此在实际工作过程中应尽量避免五维载荷的存在,降低由于滚珠受力不均对滚动直线导轨副刚性和稳定性的影响。
(2)工作载荷一定时,五维载荷的增大会使导轨副的载荷分布变差。如本文使用的SHS-25V型号导轨副,当力矩由10 Nm增大到50 Nm时,滚珠载荷分布呈倍数增大。因此在实际应用中,应尽量减小导轨副所受到的五维载荷,防止导轨副精度保持时间降低;
(3)滚珠的精度误差使滚动直线导轨副的载荷分布产生波动,且误差越大,波动越大,载荷分布越不均匀。因此选用高精度的滚珠可有效改善滚动直线导轨副中载荷分布不均的现象,提高装配精度,进而减少磨损,有利于样件使用寿命的增加。

