五轴数控机床旋转轴误差辨识及补偿*

胡金龙，李 杰，陶文坚，徐 强

(航空工业成都飞机工业(集团)有限责任公司，成都 610031)

0 引言

RTCP功能在数控加工中具有重要用途，凡是自由曲面上具有法向要求的运动轨迹控制均需要RTCP[1]。尤其是歼击机上构成飞机机身、机翼气动流线外形的框、梁、肋等倾角连续变化的斜直面外沿条成型加工，均需要RTCP功能控制螺旋铣刀空间位姿[2]。

五轴数控机床RTCP精度很大程度取决于数控系统中保存的结构参数与实际机械结构参数的一致性。当五轴数控机床在使用过程中因机械结构变形、磨损、振动冲击、铣削力及设备碰撞事故等导致实际结构参数与数控系统中保存的结构参数出现偏差，数控系统依然按照保存的结构参数控制实际结构运行就会出现RTCP运动误差，表现为加工误差。

许多研究学者针对RTCP旋转轴误差进行了研究，提出多种旋转轴误差检测及建模方法。付璇等[3]用球杆仪的三种测量模式辨识出回转轴的6项误差参数，并进行了补偿实验验证。该方法每次只能检测刀尖点一个方向的误差，要完成三个方向误差检测需要三次测量，且每次误差检测均会受其他两个方向误差的影响，测得的刀尖点误差数据准确度低；Li J等[4]在R-test基础上基于改进的工装设计，改变主轴端面至标准球的偏心距离及悬伸臂长实现旋转轴6项误差求解。该方法以工装的偏心距离和悬伸臂长为依据进行计算，因此对工装测量精度要求很高，且容易引入工装测量误差。上述两种方法均以空间刚体6项自由度为依据建立误差模型，求解的结果与数控系统定义的旋转轴结构参数项不一致，需要对误差进行转换才能用于旋转轴结构参数误差补偿。华中数控[5]基于检测棒提出了双转台和双摆头五轴机床RTCP参数测量方法，精确测量转台回转中心坐标和摇篮轴偏移、从动摆动偏心距和主动摆头偏移。该方法以数控机床直线轴的位置检测为依据，检测结果受直线轴空间定位精度的影响。

针对上述方法存在的问题，使用R-test作为测量仪器，可保证刀尖点误差检测的准确度。以五轴数控机床旋转轴结构参数误差为变量，依据RTCP运动原理，基于坐标旋转变换理论建立了误差辨识模型，根据刀尖点误差数据计算旋转轴结构参数误差。该方法能准确计算出旋转轴结构参数误差，计算的误差数据无需进行转换可直接用于数控机床旋转轴结构参数补偿，有效消除旋转轴结构参数误差引起的RTCP误差。

1 RTCP原理与刀尖点误差表现形式

1.1 RTCP原理

RTCP(Rotated Tool Centre Point)刀尖点控制运动，当只有旋转轴运动时，通过相关直线轴的实时同步补偿运动，使刀具或工件上的某一特定点在空间的相对位置始终保持不变[6]。

五轴数控机床在 RTCP功能激活状态下，数控系统将根据旋转角度、转轴方向向量、偏移向量、刀具参数等数据实时同步计算出直线轴的补偿位移量及速度，以确保切削点处刀具相对工件的空间位置和姿态按正确的方式进行运动[7]。RTCP运行原理如图1所示，机床坐标系O-XYZ下，旋转点P1(P2)至主轴端面的距离为L0，刀长值Lx，刀具半径r，则旋转点至刀尖点的距离为Rx=L0+Lx。摆动轴初始状态①(摆角a1)，顺时针旋转Δa至状态②(摆角a2)，旋转运动过程中刀尖点从T1运动至T2，刀尖点划过的轨迹为夹角Δa半径Rx的圆弧。为了保证刀尖点位置不变，需要直线轴平移补偿，使关节点从P1点运动至P2点到达状态③，补偿旋转轴产生的刀尖位移。

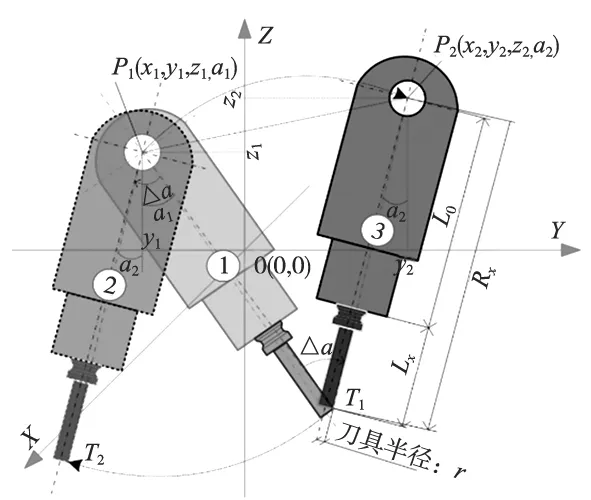
图1 RTCP运动原理

1.2 五轴数控机床旋转轴结构参数

五轴数控机床一般由两个旋转轴组成，旋转轴不同安排形式构成不同结构的数控机床[8]，五轴数控机床三种常见结构形式如图2所示。图3为西门子840D数控系统对双摆头机床旋转轴结构参数的定义实例，BASE_TOOL(AB)定义了主轴端面至第二旋转轴的偏移矢量，JOINT_OFFSET(BC)定义了第二旋转轴至第一旋转轴的偏移矢量，PART_OFFSET(CA)定义第一旋转轴至主轴端面的偏移矢量。

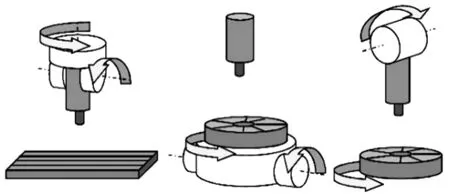
(a) 双摆头结构 (b) 双转台结构 (c) 混合结构图2 三种结构形式数控机床

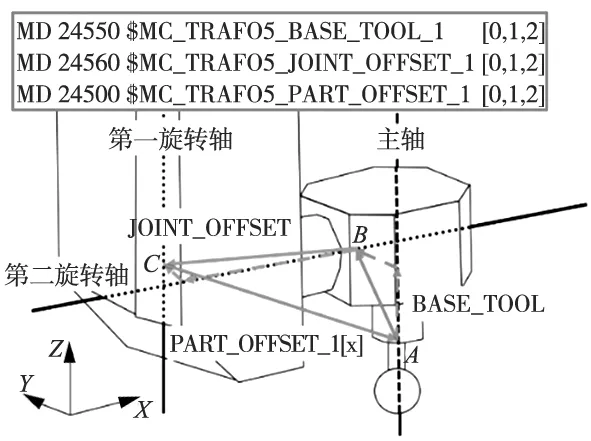
图3 西门子840D旋转轴结构参数的定义

1.3 旋转轴结构参数误差在刀尖点的表现形式

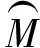
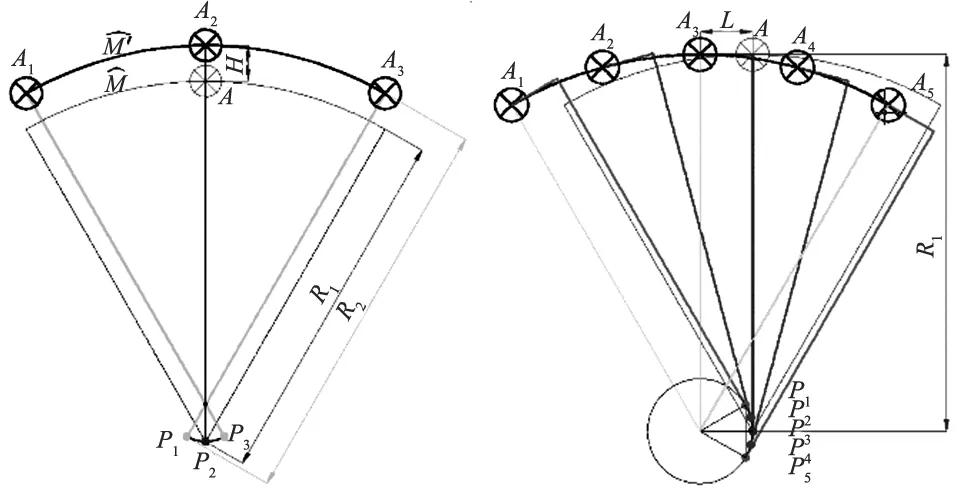
(a) 转心矩误差作用下的刀尖点误差 (b) 偏心误差作用下的刀尖点误差

2 旋转轴结构参数误差建模

数控机床定点RTCP运动过程中旋转轴结构参数误差与刀尖点误差具有确定的对应关系，因此可以建立旋转轴结构参数误差与刀尖点误差映射模型。以图5所示BA结构数控机床为例，其他结构机床采用相同分析方法。检测过程中为了减少误差影响因素，简化误差分析模型，按照ISO 10791-6[10]AK1和AK2运动检测轨迹，分别检测两个旋转轴结构参数误差。检测B旋转轴结构参数误差时，采用AK2轨迹，仅旋转轴B转动，直线轴XZ联动做补偿运动，实现定点RTCP运动；检测A旋转轴结构参数误差时，采用AK1轨迹，仅旋转轴A转动，直线轴YZ联动做补偿运动，实现定点RTCP运动。旋转轴A做定点RTCP运动简图如图6所示，坐标系OYZ原点建立在数控系统内部保存的旋转轴结构参数计算的旋转中心上， RTCP运动中刀尖点的旋转变换如式(1)，简化后如式(2)。

图5 BA结构数控机床结构参数

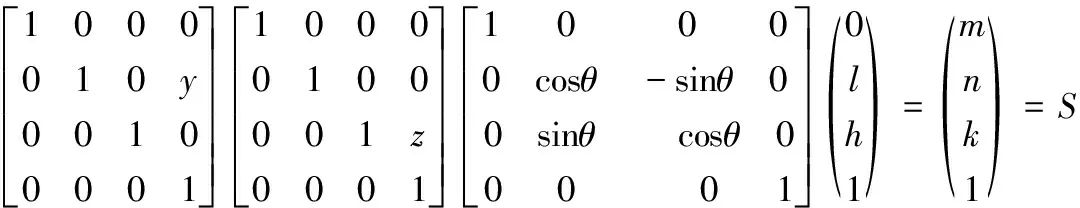
(1)

y=n+hsinθ-lcosθz=k-hcosθ-lsinθ

(2)

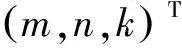
MD 24550 ＄MC_TRAFO5_BASE_TOOL_1 [0]=0

MD 24550 ＄MC_TRAFO5_BASE_TOOL_1 [1]=l

MD 24550 ＄MC_TRAFO5_BASE_TOOL_1 [2]=h

y,z表示AK1运动直线轴Y、Z运动量。

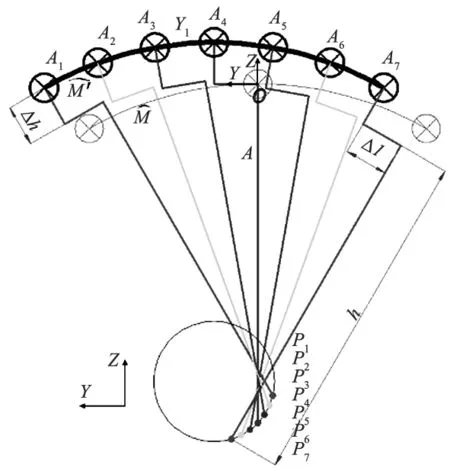
图6 摆臂长度和偏心误差综合作用下误差模型

(3)

(4)

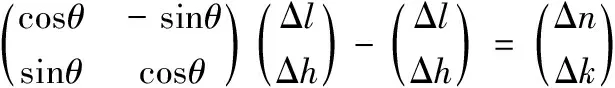
(5)

根据误差模型(5)，计算在摆臂长度误差ZOA=0.08 mm与旋转轴偏心误差YOA=0.08 mm以及二者共同作用下AK1运行过程中对应的刀尖点误差变化如图7所示。

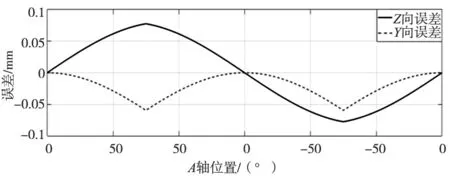
(a) YOA误差导致的刀尖点误差

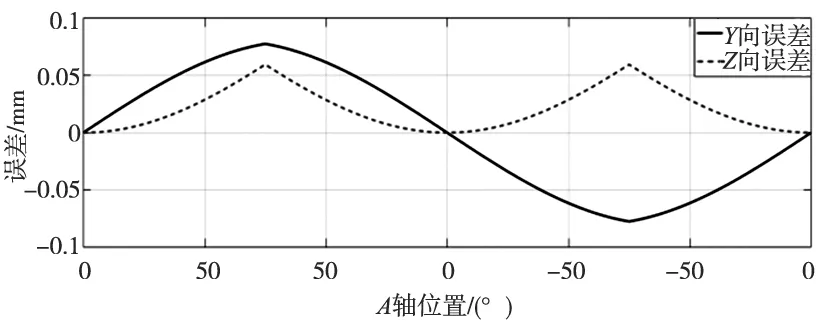
(b) ZOA误差导致的刀尖点误差

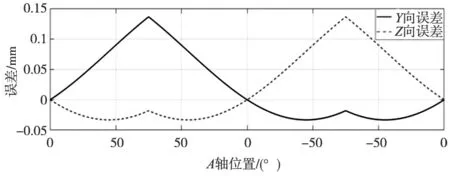
(c) YOA和ZOA误差同时作用下的刀尖点误差图7 误差模型求得的刀尖点误差曲线

3 误差模型求解

根据误差模型(5)，只要能获取定点RTCP运动过程中某一个位置旋转轴摆角及刀尖点误差数据，即可根据误差模型求解旋转轴结构参数误差。但数控机床在运行过程中会受各种偶然因素干扰引起刀尖点误差，同一个角度不同运动方向刀尖点误差也有差异，为了使得通过刀尖点误差求解旋转轴各项结构参数误差能够反映平均水平，使得结构参数补偿进数控系统后误差得到控制，每个旋转轴RTCP运动过程中同一个采样点正反两个运动方向均进行一次采样，采样点均分在旋转轴行程范围内。

为了求解A轴结构参数误差，采集A轴参与定点RTCP(AK1)运动过程中摆角在α、β、α、-α、-β、-α处刀尖点误差，其中[-β、β]为旋转轴运动范围。

表1 测量点上刀尖点误差

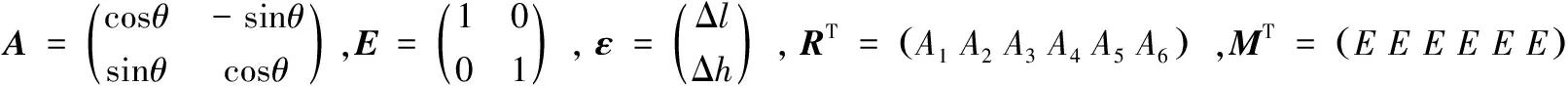
λT=(μ1δ1μ2δ2μ3δ3μ4δ4μ5δ5μ6δ6)

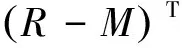
4 实验验证

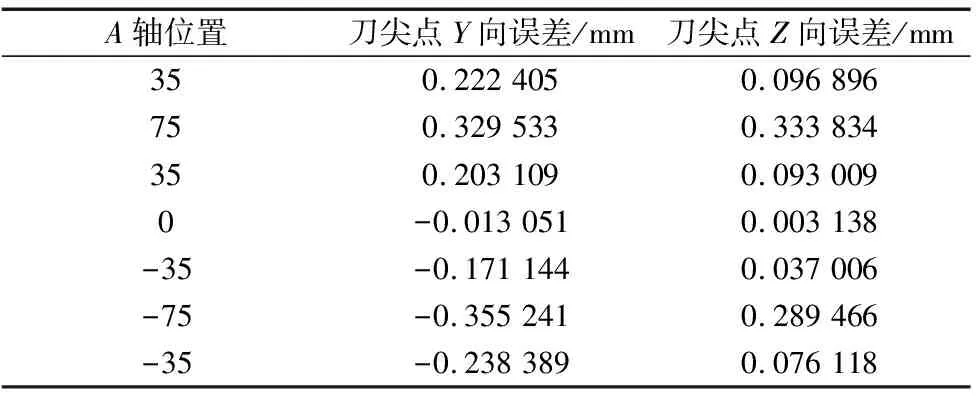
表2 AK1运动刀尖点误差数据

在CA结构机床使用R-test仪器(旋转轴分析仪)采集AK1运动刀尖点误差。A轴运动路径：0°→75°→0°→-75°→0°，相邻两个采样点间隔5°，采集到的刀尖点误差分布如图8所示，误差空间分布见图9，通过图9d可以看出误差主要由旋转轴转心距误差ZOA引起。取其中7个刀尖点误差数据计算旋转轴A结构参数误差，数据列表如表2所示。根据采集到的刀尖点误差数据及旋转轴角度，带入误差模型(R-M)T(R-M)ε=(R-M)Tλ求解得：

Δl=0.023 4 mm,Δh=-0.375 7 mm。

λT=(0.222405 0.096896 0.329533 0.333834

0.203109 0.093009 -0.013051 0.003138

-0.171144 0.037006 -0.355241 0.289466

-0.238389 0.076118)

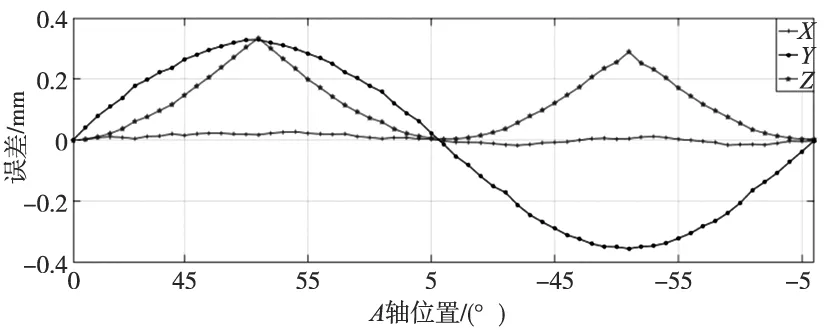
图8 补偿前AK1运动刀尖点误差

按照误差模型求解得旋转轴误差YOA=0.023 4 mm，ZOA=-0.375 7 mm。将误差值补偿进数控系统，采集到的刀尖点误差分布见图10，误差空间分布如图11所示，与图8对比可以看出刀尖点误差明显得到控制，补偿后AK1运动刀尖点误差明显减小，误差减小约88.2%。从图9和图11d可以看出，补偿后因旋转轴结构参数误差引起的刀尖点误差基本消除。

补偿前误差限：0.289466+0.355241≈0.645 mm

补偿后误差限：0.041878+0.034100≈0.076 mm

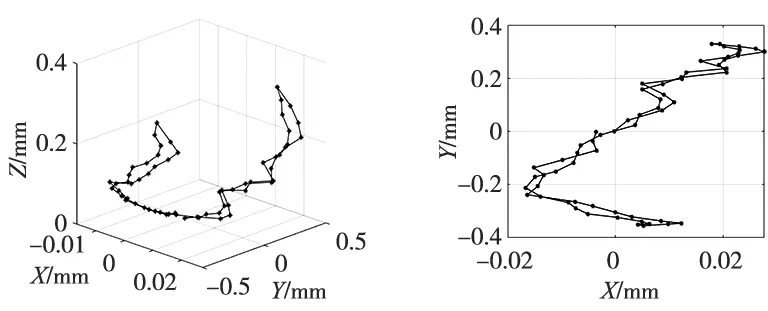
(a) 刀尖点误差空间分布 (b) 刀尖点误差XY平面投影

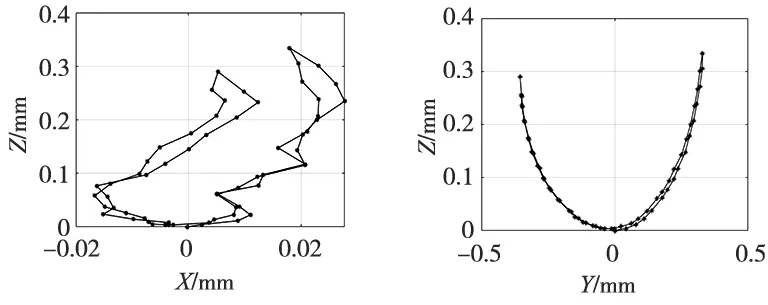
(c) 刀尖点误差XZ平面投影 (d) 刀尖点误差YZ平面投影图9 补偿前AK1运动刀尖点误差空间分布

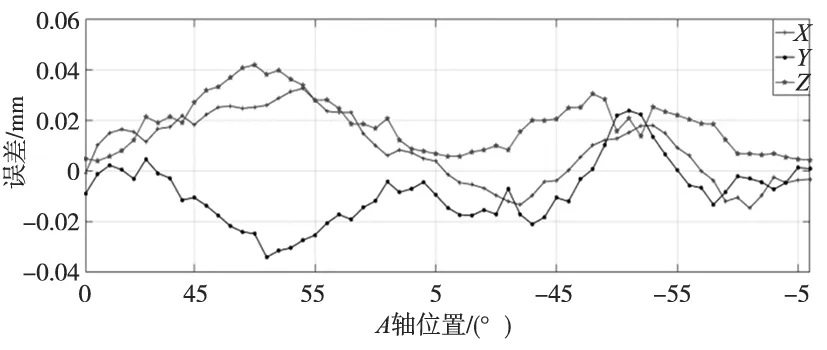
图10 补偿后AK1运动刀尖点误差

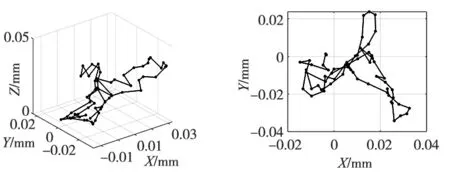
(a) 刀尖点误差空间分布 (b) 刀尖点误差XY平面投影

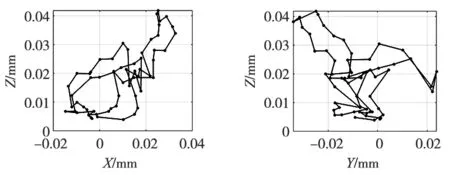
(c) 刀尖点误差XZ平面投影 (d) 刀尖点误差YZ平面投影图11 补偿后AK1运动刀尖点误差空间分布

5 结论

为了提高五轴数控机床RTCP运动精度，本文基于RTCP运动刀尖点误差，提出了旋转轴结构参数误差溯源及补偿方法，具有如下优势：

(1) 所提出的误差建模及溯源方法适合各种结构五轴数控机床旋转轴结构参数误差辨识，具有广泛的适用性。

(2) 所采用的结构参数误差计算方法可有效减少不确定性因素干扰对结构参数误差计算准确度影响，能够消除旋转轴结构参数误差对RTCP精度的影响。

(3) 通过少量的刀尖点误差数据即可实现旋转轴结构参数误差溯源，可减少数据采集的工作量及运算量。计算结果与数控系统中旋转轴结构参数项对应，无需转换即可用于误差补偿。

虽然本文所建立的模型是基于A旋转轴，但该方法具有通用性。基于该方法改变旋转矩阵及对应的参与RTCP运动直线轴平移矩阵即可以建立B旋转轴和C旋转轴误差辨识模型。