基于复合权重的模糊物元磨削工艺优化*

曹满义,徐颖杰,郑鹏,常景景

(1.郑州大学机械与动力工程学院，郑州 450001;2.郑州机械研究所有限公司,郑州 450052)

0 引言

工业磨削是机械加工中一种机理极其复杂的减材制造工艺。在工件磨削加工过程当中，工艺参数设置是否得当会对产品表面质量产生非常明显的影响。在精密加工中，磨削工艺参数甚至直接决定产品加工质量的高低。因此，磨削工艺参数组合优化对于提高产品表面完整性和生产效率至关重要。

为了综合评价磨削结果，很多学者提出了新的评定模型。如采用灰色关联分析方法可以求得各磨削工艺参数与磨削结果之间的关联度，并通过加权灰靶决策法综合评价磨削参数[1]；也可利用正交结果分析对工艺、经济、环境和健康效益综合评价获得综合最优参数组合[2]；通过MNRL建模并利用响应面法，结合蒙特卡罗技术得到砂轮最优磨削参数[3]，也有学者通过改进切入模型，优化控制系统获得最优工艺参数组合[4]。

然而，上述工艺参数优化过程过于繁琐，且由于单目标评定标准下得出的结果往往不相容，直接利用单项评价标准往往难以做出确切判断。此外，在根据单项特征确定权重时，或主观赋权，或客观赋权，导致综合评价结果或受决策者主观判断影响较大，或过于依赖实际的问题域而导致决策者的可参与性较差。

对于单目标评定的不相容问题，本文利用模糊物元描述方式，并使用模糊集合和关联度评定的方法，可较好地解决。将灰色关联法计算所得的客观权重和层次分析法所得的主观权重进行复合，兼顾实验数据逻辑性和决策可参与性，可很好避免权重分配不合理之处。将两种改进方法结合，可实现对磨削工艺参数组合进行快速有效地优化。

1 模糊物元模型

1.1 复合模糊物元

(1)

1.2 优化原则

在尚未确定工艺参数的优化方式时，可以先采取从优隶属度作为优化标准。从优隶属度可视为某一模糊量值，与该量值所处特征下最优量值的接近程度[5]。

在磨削加工中，考虑评价参数受工艺的影响，从优隶属度的计算，多采用如下模式：

正向指标:

(2)

负向指标:

(3)

其中，μij表示j事物第i项特征的从优隶属度。

(4)

1.3 关联变换

关联系数本应由关联函数求出，但由于在磨削参数寻优过程中，经典域与节域重合，故关联函数与隶属函数等价，关联系数ξij可由隶属函数值(即隶属度)加以确定[6]。因而有:

ξij=μij=μ(Xij)

(5)

这里，ξij表示j事物与理想最优事物间关于第i项特征的接近程度。经关联变换后可将隶属度转换为关联系数，构建关联系数复合模糊物元[6]，记为Rζ。

(6)

2 复合权重计算

主观赋权在决策者视属性重要程度自由分配权重时较为便利，但主观因素影响较强，不同决策人员可能会得出不同的权重，客观性较差；而客观赋权逻辑性较强，但不能体现决策者对不同属性的重视程度[5,7,9]，可参与性较差。充分运用两种赋权方法的优势，选择层次分析法和灰色关联分析法得到各评价参数对磨削结果评判的主、客观权重，并通过复合和归一化处理，获得综合考虑主、客观因素影响的复合权重。

2.1 客观权重的确定

灰色系统是指研究对象具有少部分信息可知的系统，可通过对系统有限可观测数据的挖掘，得到各单项评价参数对综合结果的贡献率。由贡献率表示权重，可消除各评价参数的权值计算过程中人为干扰，使结果更符合客观规律[2,9-10]。其计算过程如下：

(1)数据无量纲化

为避免物理量纲不同而对评定结果产生影响，本文采用区间值像处理方法，获得物元归一化原始值。

设原始数据是由m个事物n项特征组成的复合物元，则称:

(7)

为其区间值像，其中i=1,2,…,n;k=1,2,…,n;j=1,2,…,m。

(2)建立归一化评价矩阵

(8)

(3)设定参考序列

(9)

(4)求差序列

(10)

(5)求极差最大值与最小值

(11)

(6)求关系系数

(12)

其中，μdc∈(0,+∞)是区分系数，用于调整极差对关系系数的影响，避极差最大值对关联结果产生过多影响。

(7)建立关系系数矩阵

在求取关系系数之后，可建立关系系数矩阵：

(13)

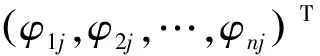
(8)求各特征贡献率

(14)

归一化处理

(15)

该值可作为由分析原始数据逻辑关系而得的客观权重。

2.2 主观权重确定

层次分析的思想是将需要确定权重的部分按类别归为不同的层次[11]。根据不同层次的要求和所期望实现的结果，将层次分解为不同的决策单元，并按照这些决策单元的关联影响，将单元归为不同层次并进行组合，形成单目标多层次结构模型[5]。最终，对同一层内的单元进行对比可得出结构单元在本层次中所占的比重。

其分析步骤如下：

(1)构建判断矩阵

判断矩阵采用两因素之间互相比较作为基本方式。以标度表明不同因素之间相比较时，不同因素对该层目标的贡献程度之比，用aij表示。

(16)

各因素的权值为上述判断矩阵的最大特征根λmax所对应的特征向量ω=[η1,η2，…,ηn]。

(2)一致性检验

定义一致性指标CI和一致性比率CR为：

(17)

(18)

其中，RI为随机一致性指标，其值与因素数n的关系如表1所示。

表1 一致性指标值

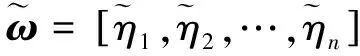
层次分析法求取主观权重的流程如图1所示。

图1 层次分析法流程图

2.3 复合权重确定

(19)

据此可求得复合权重物元

Rw=[w1,w2,…,wn]

(20)

3 关联度和综合评价

关联度是指两事物间的关联程度[5]。本文所使用的关联度，是指工艺参数组合j与各单项评价均最佳的理想组合的贴近程度，用Kj表示。

因单项特征与理想最优方案之间的评价系数比较分散，不利于从整体对方案进行评估，故需对各方案单项特征的关联度进行集中处理。

设Rk表示由m组评价参数的关联度所组成的复合模糊物元。对评价参数的关联系数采取加权集中处理，则得：

Rk=Rw*Rξ

(21)

这里“*”表示运算模式。结合磨削质量评定的需要，采用M(·,+)模式，即先将各评价指标与其对应的复合权重相乘后进行加运算。则关联度的计算公式为：

(22)

将式(6)和式(19)带入式(22)，可得到各评价参数的关联度Kj和关联度物元Rk。

Rk=[K1,K2,…,Km]

(23)

在确定各方案的关联度后，由于工艺参数只需得到一组最优组合，因此使用最大关联度作为评判原则。记所有实验结果中关联度的最大值为K*，此关联度表示在所有工艺参数组合中，该方案的磨削质量与理想最优质量最为接近，对应的工艺参数组合即可作为磨削加工最优方案。

4 实验

4.1 实验步骤

实验装置选择高精度外圆磨床MGB1320E，如图2所示。磨削工件尺寸为φ24×28 mm，砂轮规格P380×32×120 A 36 L 5 V 35，选择浓度4%极压乳化型切削液清洗，磨削方式采用外圆径向切入磨削。

综合考虑对磨削质量有较大影响的诸多因素，选择工艺参数如下：砂轮线速度A(m/s)、工件转速B(r/min)、工件硬度C(HRC)、砂轮已加工用时D(min)、粗磨进给量E(μm)、粗磨切入速度F(in/min)、精磨进给量G(μm)、精磨切入速度H(in/min)、光磨余量I(μm)。考虑生产工艺和检验效率，选择最具质量代表性的单件生产时间K(s)、工件尺寸精度L(mm)、表面粗糙度M(μm)、工件圆度N(μm)作为工件评价特征[12]。

单件生产时间由机床量仪计时程序自动记录，尺寸精度由立式光学比较仪利用相对测量法获得偏差值，表面粗糙度由光切显微镜测得，圆度由量仪采样后计算得出。

为了既能利用少量评价参数特征点与工艺参数特征点得出磨削系统的整体特征，又尽可能减少实验次数，采用正交实验表对工艺参数组合进行排序。本次实验中，设计9因素4水平L32(49)正交实验，通过部分工艺参数组合了解对评价参数的影响。工艺参数水平表如表2所示。在得出实验结果评价参数值后，根据工件生产加工技术要求和企业规定的合格标准，对评价参数合格性做如下要求：磨削加工用时K≤22 s、尺寸精度|L|≤0.006 mm、工件表面粗糙度M≤0.45 μm和工件圆度N≤3 μm。针对工件尺寸精度特征L存在负数的情况，为方便计算，取其绝对值。剔除任一单项评价指标不合格工件之后，工艺参数及相应评价参数数据如表3所示。

图2 实验装置

表2 实验参数设置

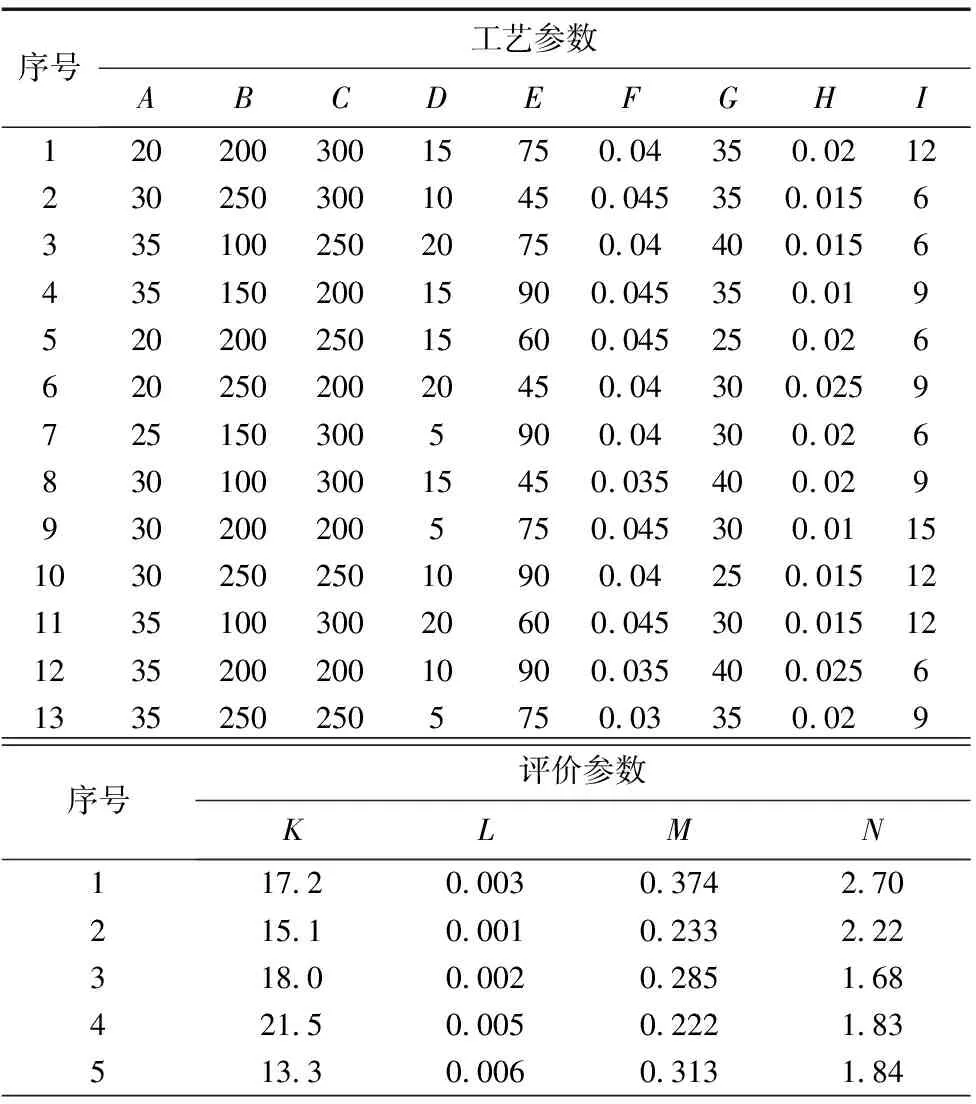
表3 合格工件参数

续表

4.2 评价模型

(1)构建复合模糊物元

以合格品工艺参数组合为事件，以评价参数K、L、M、N为特征，以评价参数测得值为数值，建立R4×13复合物元。

(24)

(25)

(2)根据关联变换求得关联变换复合物元Rξ

经关联变换，由式(5)可将隶属度转变为关联系数，并得到关联系数复合物元。

(3)利用灰色关联分析确定客观权重

根据2.1节计算步骤，取区分系数μdc=0.5以补偿极差最大值的影响，所有评价参数均为负向指标。利用灰色关联分析可求得各评价参数的客观权重如表4所示。

表4 评价参数客观权重

(4)利用层次分析法求客观权重

根据评价参数在磨削质量评估中所占的比重，结合专家意见，确定评价参数标度为a21=1，a31=4，a41=4。

由此可构造判断矩阵A：

(26)

上述矩阵为一致阵，由一致阵的性质可知该方阵自然满足一致性要求，不需要调整。求得主观权重如表5所示。

表5 评价参数主观权重

(5)计算综合权重

由式(19)计算综合权重如表6所示。

权重复合示意图如图3所示。

表6 评价参数复合权重

图3 权重复合示意图

(6)计算关联度

在得出各评价参数的关联系数和复合权重后，由式(22)可以计算出各组合格产品的评价参数与理想最优结果的关联度，列于表7。各组评价参数关联度图样如图4所示。

表7 各组评价参数关联度

图4 关联度图样

4.3 结果分析

将计算所得的13组合格品的关联度结果进行比较可知，K*=0.77。最大关联度所对应的第三组工艺参数组合即可认为是本实验所求最优组合，如表8所示。该寻优结果与加权灰靶寻优结果一致[1]，证明基于复合权重的模糊物元分析对磨削多目标工艺参数寻优是可行的。

表8 最优工艺参数组合

基于此方法优化磨削工艺参数组合，可实现在得到相似的尺寸精度和表面粗糙度时，加工效率提高12.7%(对比试验3和9)。若加工效率降低4%，则可实现尺寸精度至少提升50%、表面粗糙度提升31.2%、圆度提升37.7%(对比试验数据组3和组1,10)。在损失3.85%表面粗糙度条件下，实现圆度提升70.8%(对比试验数据组3和组9)；且此工艺参数组合得到的圆度值最小，说明利用此工艺参数组合加工的机械产品形状误差最小，这对于轴类零件的误差控制至为重要。

由实验对比可知，利用该工艺参数组合对磨削结果的优化效果十分显著。在实际生产中，可根据实际加工需要对工艺参数进行调整，在不额外增加成本的条件下提升产品质量。

5 结论

影响磨削加工质量的工艺参数众多，且相互之间的影响错综复杂。本文利用模糊物元理论进行磨削工艺参数组合优化，借助关联度的概念对磨削结果进行综合评价。在计算关联度时，利用灰色关联贡献度计算客观权重，利用层次分析法增加决策过程的可参与性，并通过权重复合增加决策的严谨性。实验结果证明，该方法能迅速准确地寻得最优工艺参数组合，具有较高的实用价值。