基于快速扩展随机树的机械臂路径优化算法研究*

杨大庆 ，谷侃锋

(1.中国科学院沈阳自动化研究所，沈阳 110016；2.中国科学院机器人与智能制造创新研究院，沈阳 110169；3.中国科学院大学，北京 100049；4.沈阳自动化研究所(昆山)智能装备研究院，江苏 苏州 215347 )

0 引言

随着科学技术的迅速发展机器人技术的逐渐成熟，工业机器人凭借其效率高、稳定性好、精度高等特点被广泛运用于焊接、装配、搬运以及喷涂等作用环境中，在劳动密集型产业向自动化生产转型过程中发挥着不可替代的作用[1-2]。其中障碍环境下机械臂操作在工业应用中占据很大比例，如何快速高效的完成机械臂运动，提高工业化生产的生产效率，使机械臂适应工业化生产过程中狭小操作空间，减低工业生产空间成本一直是机械臂研究的重点。

传统工业环境中机械臂运动路径的获取一般通过示教法复现或者通过虚拟平台规划机械臂的运动路径[3]，但是通过示教法获取机械臂运动路径耗时，不适用于变化的工业化生产，通过虚拟平台规划机械臂运动路径一般采用基于节点采样的快速扩展随机树(Rapidly-Exploring Random Tree，RRT)算法[4]在关节空间规划运动路径，这种方法难以获取笛卡尔空间下机械臂末端的最短路径。文献[5]提出了一种改进的快速扩展随机树算法，实现了串联机器人在三维避障工作空间中的路径规划问题，但没有考虑机械臂运动最短路径问题。文献[6]针对快速扩展随机数算法缺乏向导性同时规划空间大算法复杂度高问题提出目标偏置与步长控制的改进RRT算法，提高的算法的效率，但其路径可能不最优。文献[7]提出了雅克比转置定向快速扩展随机树算法，可以有效生成高维空间操作问题的解。

在分析了快速扩展随机数算法基础上提出一种笛卡尔空间下改进的快速扩展随机树算法(DL-RRT)，实现笛卡尔空间内最短距离路径规划，通过控制算法扩展步长，保证机械臂求逆解的连续性，然后对所得笛卡尔空间路径进行优化，去除路径中的冗余路径点，最后利用三次样条函数对轨迹进行规划，保证机械臂笛卡尔空间运动轨迹的平滑，减少运动过程中不必要的冲击，提高机械臂的运动效率。

1 最短距离路径规划

传统基于RRT算法的机械臂路径规划发生在机械臂的关节空间，以机械臂关节空间满足式(1)最小位移为参数求取最短行程解，没有考虑机械臂笛卡尔空间的运动轨迹，而机械臂关节空间的最小位移往往不能得到笛卡尔空间下的最小位移最优解，关节空间最小位移通式为：

(1)

式中，wi为机械臂每个关节角度变化的加权系数，Δθi为每个关节的角度变化值，为使机械臂得到笛卡尔空间下机械臂末端最短运动路径，满足工业障碍环境下狭小操作空间要求，提高机械臂工作效率，采用改进RRT算法DL-RRT算法在笛卡尔空间下对机械臂进行路径规划。

1.1 DL-RRT算法

DL-RRT算法在笛卡尔空间进行采样。首先，从机械臂笛卡尔空间起始节点qinit出发，以qinit为树状数据存储结构的根，在笛卡尔空间内随机采样获取随机节点qrand，遍历树状数据存储结构，获取距离qrand节点最近的结点qnear，在qnearqrand方向上以qnear为起点扩展新节点qnew，对节点qnew利用求逆解器求逆解，若解存在，判断节点qnew是否与障碍物发生碰撞，若发生碰撞，则节点qnew丢弃，重新采样，否则将节点qnew加入到树状数据存储结构中。若逆解不存在，节点qnew丢弃，重新采样，直到采样节点qnew=qgoal，算法结束，否则继续采样扩展新节点，DL-RRT算法在笛卡尔空间采样过程如图1所示。

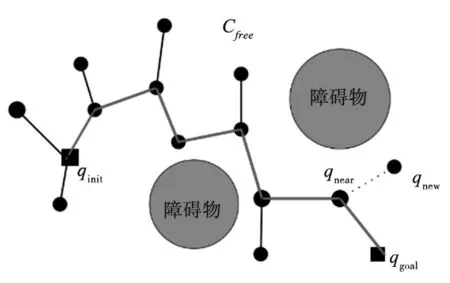
图1 RRT算法扩展图

由于机械臂求逆解过程中可能存在多组解，为保证机械臂运动路径的连续性。设计机械臂逆解求解器，求解器对节点qnew的多组解进行遍历，利用关节最小位移原则找出距离节点qnear最近的一组解作为节点qnew，保证机械臂运动过程中关节运动平稳。

1.2 目标偏置与贪婪策略

传统的RRT算法由于随机采样，节点树结构均匀向周围扩展，当搜索空间过大时，算法效率降低。为提高RRT算法的搜索效率，在RRT算法中加入目标偏置参数，设置目标偏置概率Pgoal，使节点采样以概率Pgoal将目标结点qgoal设置为随机节点qrand，促进结点树向目标发现扩展，减少节点树向不必要的方向扩展同时保留节点树探索未知区域的能力，提高节点树的搜索效率。

为提高节点树的扩展效率，文献[8]提出了一种贪婪算法，在节点树扩展节点时，如果新节点与障碍物不发生碰撞，则保持节点在该方向继续扩展。在此基础上，在DL-RRT算法基础上加入贪婪策略，提高节点的扩展效率。加入目标偏置与贪婪策略的DL-RRT算法具体步骤如下：

(1)初始化节点树结构，将初始节点qinit加入到节点树中作为根节点。

(2)在笛卡尔空间基于目标偏置策略采样，设置偏置概率Pgoal，当产生的随机树小于Pgoal时，将目标结点qgoal设置为随机节点qrand，当随机数大于Pgoal时，在笛卡尔空间内随机采样。

(3)遍历节点树，查询距离qrand最近的节点qnear，在qnearqrand方向上以qnear为起点以固定步长L扩展新节点qnew，对节点qnew求逆解，若解不存在，返回步骤(2)重新采样。

(4)若节点qnew求逆解存在，判断节点qnew是否与障碍物发生碰撞，若发生碰撞，返回步骤(2)重新采样。

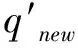
2 路径优化

由RRT算法可知，算法在整个搜索空间内均匀采样，在使用目标偏置策略与贪婪采样的情况下，节点采样仍有可能偏离目标造成路径上节点的大量冗余，导致规划路径达不到最优，因此有必要删除路径中不重要的节点，比较LOS(Line of sight path pruning)与GPP两种方法，GPP克服了LOS短视的缺点并且计算效率高，因此使用GPP算法优化机械臂运动路径，具体步骤如下：

(1)初始化优化路径数据存储结构Opath，令qstart为待优化路径path的第一个节点，并且将qstart存储进Opath，令qend为待优化路径中qstart的下一个节点，判断qstart与qend是否有障碍物。

(2)若存在障碍物，将qend的前一个qend-1存入Opath，令qstart=qend-1，qend为待优化路径path中qstart的下一个节点，继续搜索，直到qend为优化路径path最后一个节点，将qend加入到Opath中。

通过GPP算法优化以后结果如下图所示，图2为俩次试验下DL-RRT算法原始规划路径，存在大量冗余节点，这些节点不能刻画路径的关键位置信息，并且规划路径曲折线段较多。经过GPP算法优化之后，结果如图3所示，规划路径删除了路径中的冗余点，保留了规划路径关键路径点特征。

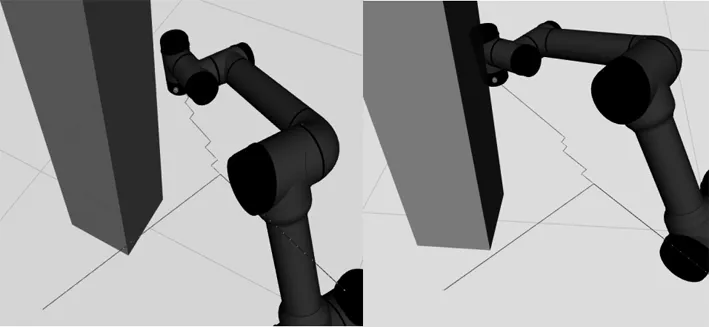
图2 DL-RRT算法效果图

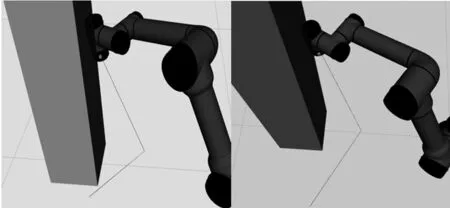
图3 GPP算法效果图

机械臂路径经过GPP算法优化之后，路径中会存在曲线折段，造成机械臂末端轨迹不平滑，在运动过程中可能会发生抖动，同时会造成运动过程不连续，影响机械臂运行效率，采用三次样条插值的方式对经过GPP算法优化之后的路径进行平滑处理，使机械臂末端轨迹平滑，减少运动中的停顿，防止运动过程总抖动的发生。如图4所示，俩次试验下规划路径平滑结果，经过三次样条插值之后的机械臂末端路径平滑，没有与障碍物发生碰撞。

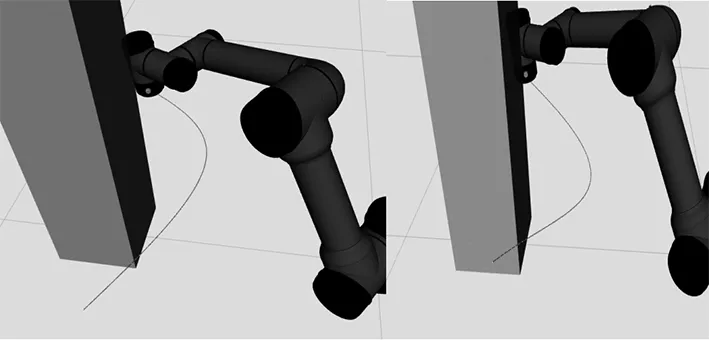
图4 路径拟合效果图

3 仿真实验

为检验DL-RRT算法的有效性，以aubo_i5串联机械臂为实验对象，在ros机器人操作系统下基于moveit_rviz搭建机械臂仿真实验平台，对关节空间下的RRT算法与DL-RRT算法效果进行比较。

设定传统RRT算法与改进(DL-RRT)算法采样迭代次数均为为1000，传统RRT算法采样步长为3，DL-RRT算法采样步长为0.01贪婪限制次数为20，其中蓝色物体为障碍物。实现结果如图5、图6所示，图5a与图5b展示了不同角度下观察传统RRT算法关节空间的规划路径，传统RRT算法规划路径所需操作空间更大，末端机械臂运动轨迹更长，DL-RRT算法规划路径如图6a与图6b所示， DL-RRT算法得出笛卡尔空间下的机械臂末端相对最优路径满足机械臂末端最短路径要求，所需要的操作空间相对于传统RRT算法更小。

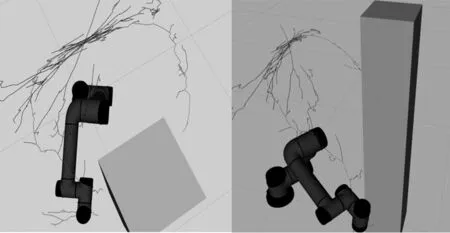
(a) 路径俯视图 (b) 路径轴对称视图图5 传统RRT算法关节空间规划路径

(a) 路径俯视图 (b) 路径轴对称视图图6 DL-RRT算法规划路径

4 结论

针对工业障碍环境中狭小操作空间下机械臂运动，基于传统RRT算法的基础上设计了DL-RRT算法，对机械臂在笛卡尔空间下进行路径规划，得出机械臂笛卡尔空间下的最短路径，相对于传统RRT算法在机械臂关节空间规划所得路径， DL-RRT算法规划路径在笛卡尔空间下距离更短，机械臂所需操作空间更小，同时采用三次样条插值算法对改进RRT算法规划路径拟合，使改进RRT算法规划路径平滑连续，降低运动过程中的抖动与停顿，减少机械臂运动时间，提高机械臂的工作效率。