基于回溯算法的多约束宿舍分配方法

王晓薇, 马佳宁, 龚雪莹, 任恩良, 孙 航

(1. 沈阳师范大学 软件学院, 沈阳 110034; 2. 沈阳工程学院 党政办公室, 沈阳 110136)

0 引 言

高校招生规模不断扩大,在校大学生的人数不断增加,这给学生管理工作带来一定的压力。而数字化、信息化校园进程的加速推进,高校的科研、教学等方面都已进入数字信息化管理时代,由此可见,使高校学生宿舍管理也实现数字化、信息化则显得尤为重要[1]。据调查,多数高校在学生宿舍管理工作上仍采用人工管理办法,但人工管理办法随机性强、工作量大,易造成宿舍资源分配不均、混乱,因此,提出一种有关宿舍智能分配的方法显得尤为重要。

宿舍分配属于多约束分配问题,此类问题依赖于分配对象和待分配资源的属性特点和特定的分配约束条件,目前应用于此类资源分配问题的算法主要有贪心算法,但在应用贪心算法进行资源分配时,每个对象的分配过程均需将该对象与待分配资源进行匹配度分析比较,导致该算法的时间复杂度较高,效率较低。

基于此,提出基于回溯算法的多约束宿舍分配方法,实现高效率的宿舍智能分配。回溯算法作为一种选优搜索法,是求解人工智能问题的基本方法之一,通过深度优先搜索,将问题的解按照一定次序进行逐一枚举及检验,若当前解不能成为问题解时,便回溯选择下一个待检验解,从而逐步得到问题的最优解。回溯算法多应用于资源分配问题、多约束条件下求解问题等,相较于把所有元素一一进行枚举研究的穷举搜索法等而言,回溯算法的效率更高[2]。因此,提出基于回溯算法的多约束宿舍分配方法,根据宿舍及学生的客观属性特点,结合分配约束条件,对宿舍实现智能分配,有效地节约了人力、时间等成本,同时提高了宿舍分配的质量,实现了学生宿舍信息化管理[3]。

1 回溯算法

1.1 算法概述

回溯算法是满足一定约束条件的最优搜索方法,该搜索方法是通过逐步确定的多阶段实现的[4]。在每个阶段,从多重选择分支中挑选出一个分支,若解不存在,则回溯到搜索到的节点并选择其他节点。若该节点所有分支经过检验,均不存在解,那么将回溯到上一节点,而原节点被称为满足回溯条件的回溯节点[5]。回溯算法应用公式如下:

回溯法=行为(逐个×××××)+约束(×××应该××××)+目标(最终××××)

回溯算法采用深度优先搜索策略,在问题的解空间树中,从根结点出发,按序搜索解空间树中的结点,判断该结点是否包含问题的解[6],若不包含,则进行剪枝,跳过对该结点为根的子树的搜索,逐层向其祖先结点进行回溯,否则,进入该子树,继续按照深度优先策略进行搜索[7],得到问题的解。

1.2 回溯算法求解模型

设问题P=(D,X,C)为三元组,其中D为值域集,X为变量集,C为约束集,n元组(X1,X2,…,Xn)构成问题的状态空间S。

Cj=V(Cj)+R(Cj)(V(Cj)为变量集,R(Cj)为关系集)

V(Cj)={Xj1,Xj2,…,Xjp}

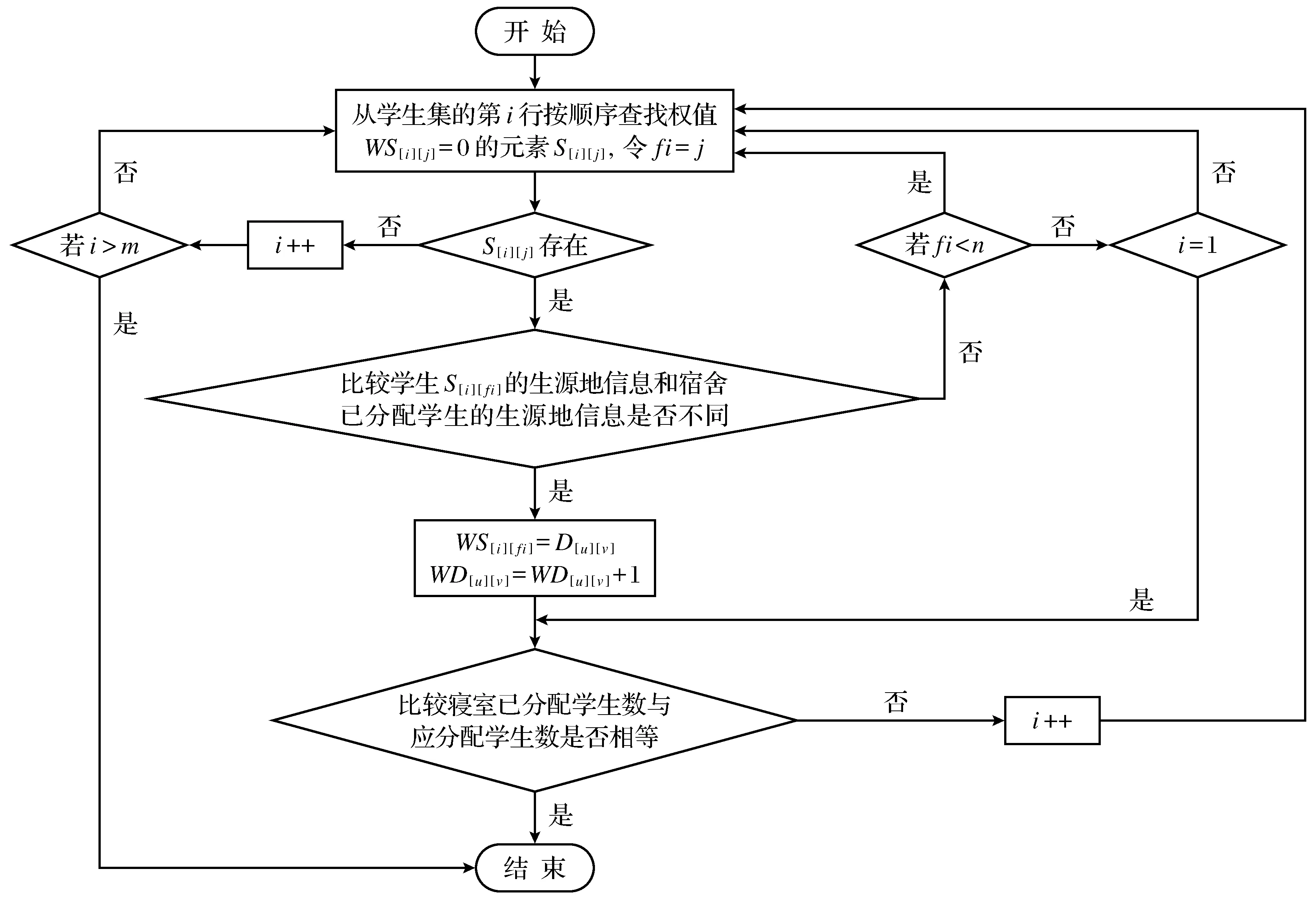
R(Cj)=R(Xj1,Xj2,…,Xjp)⊆Dj1×Dj2×…×Djn,p

S={(X1,X2,…,Xn)|Xi∈Di}

将问题P的n元组状态空间S表示为带权有序搜索树T,高为n,从T的根结点开始,对叶节点进行搜索检验,其实现方法如下:

S1k=1(1≤k≤n);

S2 如果Tk(X1,X2,…,Xk-1)的值未取完,则Xk=Tk(X1,X2,…,Xk-1)中未取过的值,否则k=k-1;

S3 若k=0,无解,End,否则转S2;

S4 若X1,X2,…,Xk约束检验为真,则k=k+1;

S5 若k=n,得到解,End,否则至S2。

1.3 回溯算法进行宿舍分配

回溯算法在多约束条件下对某一资源进行合理化分配在规划网络、优化多目标等较多领域都有着较为广泛的应用[8],故提出基于回溯算法的多约束条件下宿舍分配方法。将回溯算法应用于宿舍分配,对宿舍分配的各项约束条件进行分析,同时对宿舍资源及学生数据进行统计分析,形成宿舍集与学生集,基于约束条件,按照深度优先的搜索策略,从宿舍集的根结点出发,搜索解空间树。根据确定的约束条件以及优先级,对宿舍集解空间树进行剪枝操作,提高解搜索效率,得到最优解。当在搜索过程中无解满足约束条件时,该选择则视为不优解,当遍历了该分支的解集后仍未找到满足约束条件的解,将回溯到回溯节点进行重新选择[9],得到基于约束条件下的可接受解,完成对学生的宿舍分配。

2 约束条件分析

2.1 宏观约束条件

对于一所高校的宿舍资源,在进行分配时,首先要将学校的整体资源分配给下属各学院,此时需满足如下条件:

1) 是否跨区分配。对于同一学院的宿舍资源,要尽量保证分配的宿舍资源在同一宿舍区,方便学生日常生活以及学院的日常管理[10]。当基层学院待分配宿舍学生数较多,同一生活区的资源无法满足需求时,就会涉及到跨区分配,此时,需参考学生日常学习生活的区域范围。

2) 是否跨楼分配。当学院待分配宿舍人数较少时,参考该学院学生已分配的生活区及宿舍楼,考虑是否可以对该部分学生进行不跨楼宿舍分配,提高学院学生管理工作的便利性。

3) 宿舍客观属性。考虑宿舍本身的特性,如宿舍是否为整寝,散寝已有成员的学院、年级、专业,宿舍所在阴阳面,寝室环境的优良等,要做到合理分配。

4) 是否参考学院意愿。分配时,可让学院提出各自分配意愿,可优先按照学院的第一志愿进行分配,满足学院的自身需求。

2.2 微观约束条件

当宿舍资源分配到各学院后,学院将按需分配给学生,在此阶段,需满足以下条件:

1) 基本条件。分配时,要考虑学生的基本特性,如性别、年级、专业,尽量保证同一年级、同一专业、同一辅导员老师的学生聚堆分配,以方便学院管理以及同学间的交流。

2) 个性化条件。在满足基本条件后,可考虑有关学生的个性化特点。如根据学生生源地,尽量把生源地不同的同学分配在一起,避免仅同乡同学之间交流,使学生尽快适应环境等[11]。如根据学生入学成绩,保持不同宿舍分配学生的学习情况平衡,以便同学们能够保持良好的学习态度。

3 多约束条件下回溯算法分配宿舍

为方便计算,假设宿舍集仅属于一栋学生宿舍楼,每层的宿舍数量相等,同一层的宿舍分类相同。约束条件简化为仅考虑学生的院系、专业、班级以及生源地信息。

3.1 前期集合定义

1) 学生集。学生集是有限的,每个元素都有一系列的特性,每个人可以分别通过他们的特征来识别[12]。如学生被定义为学生集,那么学生姓名、学号、性别、所在学院、所学专业、生源地等信息,均为学生的个体特征。

2) 宿舍集。宿舍集的总量是有限的,不同的宿舍资源可以被识别[13]。在宿舍分配问题中,资源设置的要素是学生宿舍。而宿舍所在生活区、楼号、楼层、宿舍人数、宿舍可分配人数、宿舍性别分类等,为每个元素的特征。

3) 约束条件集。学生集特征和宿舍集特征之间的数学关系由约束条件组构成[14]。大学宿舍分配的主要约束条件是宿舍容纳学生性别、可容纳学生数等,且宿舍与床位之间是一对一的关系。其他约束条件由每个学生的特点决定,比如统一专业、统一班级等。

4) 解集。解集是多约束条件下学生集和宿舍集的最优对应关系。

3.2 分配过程

根据前期调查结果与实际情况分析,得出宿舍分配基本过程如下:

1) 确定宿舍及其基本信息,形成宿舍集;

2) 根据学生的院系、专业、班级,形成学生集并确定学生的需求;

3) 通过合理的分配算法得到分配结果;

4) 在分配管理过程中,记录宿舍状态和分配学生人数的动态信息。

3.3 主要信息存储矩阵

定义1 矩阵Dt×r用于保存学生寝室楼的所有宿舍,其中,t为寝室楼的层数,r为每层的宿舍数,D[i][j]为矩阵Dt×r中的元素,其值为宿舍号,i为楼层号,j为宿舍号,WD[i][j]为该宿舍已入住学生数。

定义2Dnum为宿舍应住学生的数量,Snum为需求集中的学生数量。

定义3 矩阵Sm×n用于保存学生集中所有学生的相关信息,m=Dnum,n=(Snum/Dnum)+1;S[i][j]为按院系、专业、班级升序排序后,按分数降序排列的矩阵元素;S[i][j]的值为学生学号,i为该学生所在的组号,j为该学生在其所在组的序号;WS[i][j]为该学生分配的宿舍号。

定义4 矩阵Am×n用于保存学生集中所有学生的生源地信息,矩阵元素和学生对应的规则等于矩阵S,A[i][j]的值为学生的生源地。

定义5 {S[i][fi]|i=1,2,…,m}为所选宿舍的解集,其中fi为矩阵S中所选i和j的交叉节点。

3.4 算法步骤

算法的流程图如图1所示。

图1 算法流程图Fig.1 Algorithm flow chart

从学生寝室楼D中选择足够的宿舍等待分配,然后在学生集中选择学生,根据生源地条件进行分配,主要算法步骤如下:

第1步 将宿舍集中的宿舍D[u][v]作为待分配宿舍,假设应分配学生数为Dnum,宿舍已分配学生数WD[u][v]= 0;

第2步 按顺序选择学生集矩阵S第i行WS[i][fi]=0的学生S[i][j],对其进行宿舍分配,令fi=j;如果S[i][j]存在,至步骤4;

第3步 否则令i=i+1,如果i>m,则矩阵S中的学生均已分配宿舍,end;否则,至步骤2;

第4步 将学生S[i][fi]的生源地信息A[i][fi]和宿舍已分配学生的生源地信息A[k][fk]依次进行比较;

第5步 如果A[i][fi]≠A[k][fk],那么将宿舍D[u][v]分配给学生S[i][j],WS[i][fi]=D[u][v],该宿舍的已分配学生人数加1,D[i][j]=D[i][j]+1;否则继续依次遍历矩阵S中的其他学生;

第6步 如果遍历后的结果仍无法满足A[i][fi]≠A[k][fk],设此时使A[i][fi]=A[k][fk]的行数为p;如果fi

第7步 否则,如果i=1,则此时无最优解,只能求弱约束条件的解,依次从矩阵S中选定未分配的学生,进行宿舍分配,直至宿舍D[u][v]分配完,至步骤8;否则回溯到第p行,令i=p,至步骤2;

第8步 如果WD[u][v]=Dnum,则宿舍分配工作完成,end;否则,令i=i+1,至步骤2。

3.5 时间复杂度分析

在本文所提到的多约束条件下寝室分配问题的回溯算法中, 问题的规模为m(m为学生组数,m=Hnum), 解空间树的高度为n(n为每组的人数,n=(Snum/Hnum)+1), 每次只需在学生集的同一行搜索即可, 即时间复杂度T(n)=O(n)。 相较于其他资源分配算法,如动态规划算法时间复杂度为二次函数O(n2), 而回溯算法时间复杂度为线性函数O(n), 与其他非常数阶算法的时间复杂度相比较而言, 如图2所示,线性阶函数时间复杂度的值最小, 算法的执行时间最短, 效率最优, 有效的提高了分配的效率[15]。

图2 算法时间复杂度比较图Fig.2 Comparison diagram of algorithm time complexity

4 结 语

基于回溯算法的多约束宿舍分配方法可根据宿舍及学生的特性,将具有同一院系、同一专业、同一班级等属性的学生进行智能分配,有效地降低了宿舍管理上的人力和时间成本,提高了宿舍分配的质量和效率,促进了高校宿舍管理的数字化、信息化,达到了预期的效果。同时,此方法仍有需改进的地方和提升空间,例如,如何使宿舍分配更加人性化,如何增加更多的约束条件使得分配的结果更优等,可作为继续研究的目标。