非等差非等比数列通项公式的几种基本求法

湖北

数列通项公式是高考中的重点内容，求法也多种多样，现将非等差非等比数列通项公式的求法归纳整理如下.

一、和项关系法

【例1】已知数列{an}的前n项和Sn=2n2-3n+k，求数列{an}的通项公式.

【解】当n=1时，a1=S1=-1+k；当n≥2时，an=Sn-Sn-1=2n2-3n+k-2(n-1)2+3(n-1)-k=4n-5.

若k=0，则a1=-1,符合an=4n-5(n≥2)；

若k≠0，则a1=S1=-1+k，不符合an=4n-5(n≥2).

所以当k=0时，an=4n-5(n∈N*)；

【例2】若非零数列{an}的前n项和为Sn(Sn≠0)，且a1=1,3an+1=Sn(n∈N*)，求此数列的通项公式.

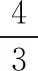
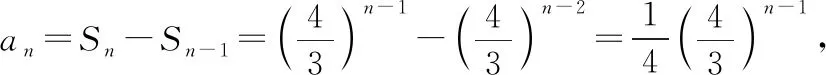
又a1=1不适合此式，

【变式1】若数列{an}的前n项和Sn=n2+2n+3，求数列{an}的通项公式.

【变式2】若数列{an}的前n项和Sn=n-5an-85，求数列{an}的通项公式.

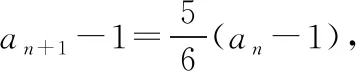
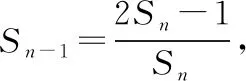
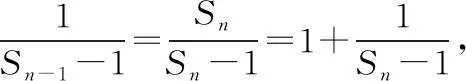
二、累加、累乘法

【例3】已知数列{an}满足a1=2,an=2·3n-1+an-1(n≥2)，求数列{an}的通项公式.

【解】由an=2·3n-1+an-1(n≥2),得an-an-1=2·3n-1,则an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2+2·3+2·32+…+2·3n-1=3n-1.

故所求的通项公式为an=3n-1(n∈N*).

【变式1】若数列{an}满足a1=2,2an+1=n(an-an+1)，求数列{an}的通项公式.

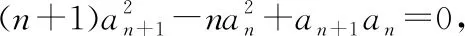
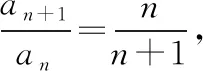
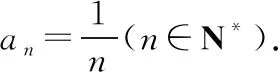
三、整体相减、相除法

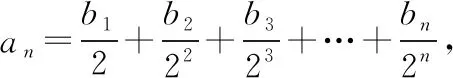
【解】由a2+a7=16，得a3+a6=16，又a3a6=55且公差大于零，

所以a3=5,a6=11，由a6=a3+3d得公差d=2.

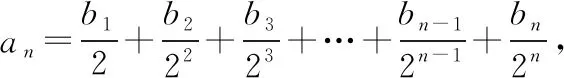
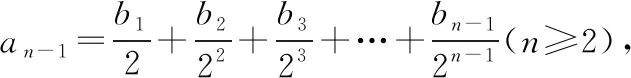
所以bn=2n(an-an-1)=2·2n=2n+1(n≥2)，③

又b1=2a1=2不适合③，

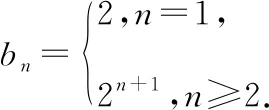
【例5】若数列{an}对任意n∈N*，都有a1·a2·a3·…·an=n2，求该数列通项公式.

【解】由a1·a2·a3·…·an=n2，①得a1·a2·a3·…·an-1=(n-1)2(n≥2)，②

【点评】如果条件关系式是由若干项的“和”或“积”的形式构成的，一般采用这种整体相减(除)或整体代换的方法求其通项公式.

【变式】若数列{an}满足a1=3,a1+2a2+3a3+…+nan=2n+1，求{an}的通项公式.

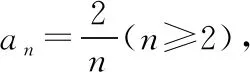
四、取倒数法

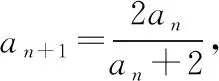
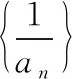
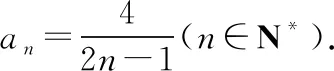
【点评】若条件递推关系式是以分式形式给出的，一般采用取倒数的方法求其通项公式.

【变式1】已知数列{an}满足3anan+1=an-an+1且a1=2，求数列{an}的通项公式.

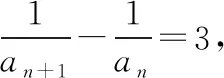
五、转化法

【例7】已知数列{an}满足a1=3,an+1=2an+1，求数列{an}的通项公式.

所以数列{an+1}是以a1+1=4为首项,2为公比的等比数列，所以an+1=4·2n-1=2n+1，

所以数列{an}的通项公式为an=2n+1-1(n∈N*).

所以数列{an}的通项公式为an=2n+1-1(n∈N*).

【另解】由an+1=2an+1,得an=2an-1+1(n≥2),两式相减得an+1-an=2(an-an-1)(n≥2)，

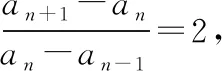
所以an-an-1=4·2n-2=2n.

所以an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=3+22+23+…+2n=2n+1-1.

故数列{an}的通项公式为an=2n+1-1(n∈N*).

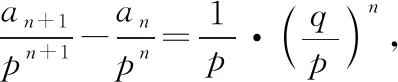
【变式1】已知数列{an}满足a1=5,an+1=2an+3n，求数列{an}的通项公式.

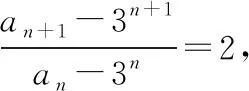
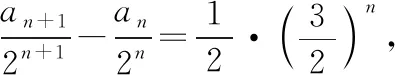
【变式2】设数列{an}满足a1=4,an=3an-1+2n-1(n≥2)，求数列{an}的通项公式.

【分析】设an+An+B=3[an-1+A(n-1)+B]，则an=3an-1+2An-3A+2B.

所以2A=2,-3A+2B=-1，解得A=B=1.则an+n+1=3[an-1+(n-1)+1].

所以an+n+1=6·3n-1=2·3n，则an=2·3n-n-1，

所以数列{an}的通项公式为an=2·3n-n-1(n∈N*).

【点评】递推式为an+1=pan+an+b(p为常数)，变为an+1+x(n+1)+y=p(an+xn+y)，则{an+xn+y}为等比数列，采用待定系数法变形.

六、乘方、开方法

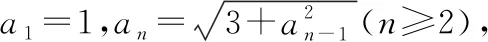
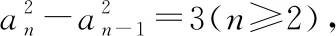
【点评】如果条件递推关系式中含有根式，一般要进行乘方与开方.

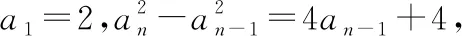
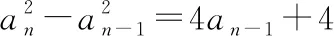
若an=an-1+2，即an-an-1=2，则{an}为等差数列，求得an=2n.

若an=-(an-1+2)，即an+1=-(an-1+1)，则{an+1}为等比数列，求得an=3·(-1)n-1-1，综上，所求an=2n或an=3·(-1)n-1-1.

七、取对数法

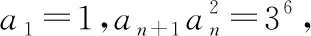
所以数列{log3an-2}是以log3a1-2=-2为首项,-2为公比的等比数列,

所以log3an-2=(-2)·(-2)n-1=(-2)n，即log3an=(-2)n+2.

所以数列{an}的通项公式为an=32+(-2)n(n∈N*).

【点评】如果条件递推关系式的两边是积、商、幂的形式，一般对等式两边取对数.

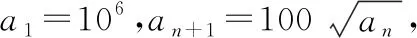
八、递推法

【例10】已知数列{an}的首项a1=1，且满足an+1=3an+1，求数列{an}的通项公式.

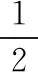
【点评】通过多次使用条件递推关系式就可以把an和a1的关系求出来，然后求出通项公式，也可以采用累加法或待定系数法求其通项公式.