基于分数阶微积分的岩石非定常蠕变本构模型

李娜,于晓要

基于分数阶微积分的岩石非定常蠕变本构模型

李娜,于晓要

商丘工学院 基础教学部, 河南 商丘 476000

基于分数阶微积分理论，对岩石蠕变本构模型中常用的Abel黏壶元件进行改进，得到表征损伤阀值效应的非定常性元件模型，并论证该模型可以良好适用于岩石加速蠕变阶段。基于经典元件组合理论，通过弹性体、Abel黏壶体以及改进后的损伤阀值触发的Abel黏壶元件体建立了新的岩石蠕变本构模型。基于实验数据反演拟合，结果表明，该岩石蠕变本构模型能良好的表征岩石蠕变三阶段，特别是非线性加速蠕变阶段，与实验数据相关程度高，误差较小，且该模型考虑的损伤阈值触发作用情况更贴切岩石蠕变行为。通过对本构模型中加载应力及求导阶数敏感度分析，获得了影响蠕变应变量的参数为加载应力，影响蠕变速率的为求导阶数，从本构模型上揭示了影响岩石蠕变行为特性的基本参数。

岩石蠕变; 分数阶微积分; 本构模型

在工程领域，常常需要对岩石进行长期变形和长期强度的预测，即岩石的蠕变变形能力研究。岩石的蠕变特性在岩石力学领域是一个重要的研究方向。对于岩石蠕变变形研究，限于时效较长，试验成本较高的问题，因而常常通过研究岩石蠕变本构模型对岩石长期变形和长期强度进行定量分析。根据岩石蠕变理论模型与实验研究可知，岩石蠕变包含了初始减速蠕变、稳态蠕变、加速蠕变三阶段。对应的蠕变本构模型需要良好概括这三个阶段，就必须引入特殊性的元件模型进行合理量化。通常来说，非线性加速蠕变阶段较难模拟，针对非线性加速蠕变阶段的特殊性，必须要构建合适的本构模型进行描述[1-3]。

随着基础数学的发展，岩石力学领域内逐渐引入较多数学模型进行岩石材料本构模型构建。蒲少云等[4]通过开展低频率动应力加载下岩石变形破坏实验，构建了岩石分数阶Burgers本构模型。何志磊等[5-7]基于分数阶导数提出了非线性蠕变模型，并借此推导出三维有限差分状态下的蠕变模型，并利用编程与室内岩石蠕变实验，验证了该模型的可靠性。陈卫忠等[8]在Burgers模型的基础上，建立起盐岩非定常Burgers蠕变本构模型，并将所建方程有限元程序化。吴斐等[9,10]通过对分数阶蠕变本构模型的改进，通过室内实验数据研究了带应力或应变触发的分数阶蠕变本构模型，并且从室内试验结果验证了该蠕变本构模型更加简单合理。苏腾等[11]研究了变阶分数阶导数的岩石蠕变模型，并从实验结果论证了模型的正确性。从上述学者研究成果可知，分数阶蠕变本构模型在岩石力学蠕变模型中具有较好的应用前景，对于岩石的非线性加速蠕变阶段具有良好的适用性[12]。

前文较多学者主要聚焦于非线性加速蠕变阶段的适用性，而对于非线性加速蠕变阶段损伤差异性却研究较少。在外部荷载的作用下，岩石内部逐渐产生损伤，当损伤积累到一定程度时，岩石发生失稳破坏，因此岩石的损伤是一个逐渐演化的过程。蠕变破坏过程同样是如此。当外部荷载维持稳定时，岩石内部也逐渐发生损伤破坏。因而，构建岩石蠕变本构模型必须要考虑模型参数损伤差异性。为此，本文将从损伤的阀值效应出发，通过改进经典模型，建立考虑岩石损伤效应下的模型元件，并构建出考虑岩石实际损伤状态的蠕变本构模型。

1 考虑损伤的分数阶非定常蠕变模型

1.1 考虑损伤的分数阶非定常Abel黏壶

在分数阶积分领域，Riemann-Liouville（R-L）积分常常被引入到岩土材料本构模型中，R-L积分的数学概念定义为[13]：在自变量为非负区间上，存在一个()可积，并定义出分数阶的函数为：

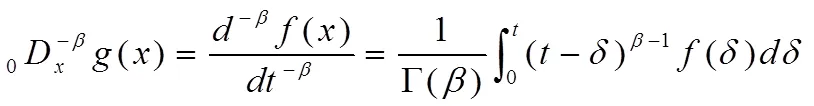
式中：Γ为广义Gamma函数，为非负非零的数，-1<<，=1,2，…，采用微积分领域中的Laplace正变换与逆变换求解。

由数学微积分转换理论可知，R-L积分微分表达式为：

目前，有学者提出了一种新的元件模型[14,15]，该元件模型既不是一种固体模型，亦不是流体模型，而是一种半固体半流体模型，该模型可表述为：

式中：为粘滞系数，当分数阶阶数为0时，该元件为弹性固体模型；当分数阶阶数为1时，该模型为牛顿流体；当分数阶为介于0~1的分数时，即为一种全新模型元件Abel黏壶，可用于描述材料的黏弹性变形。

根据蠕变实验的原理可知，岩石原始状态可认为(0)=0，根据此数学条件，进而求出积分表达式为：

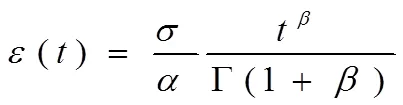
式（4）为岩石在无损伤作用下Abel黏壶的表达式。

岩石属于典型的非均质性材料，在蠕变加载过程中，其实质上是内部裂隙逐渐扩展联结贯通形成宏观裂纹失稳破坏的过程。因此研究岩石蠕变本构方程时考虑岩石在蠕变过程中的损伤时效作用很有必要，蠕变损伤时效作用将影响粘滞系数参数发生变化。根据文献[7,12]知粘滞系数在损伤作用下为减小的趋势，且呈指数衰减的态势，并给出具体函数关系式：

´=-at(5)

式中：为初始粘滞系数，为岩石材料参数。

另一方面，岩石的损伤作用是具有阀值的，应将损伤作用分两部分来考虑，损伤作用只有达到一定门槛值时才会发生。当蠕变加载应力低于损伤阀值时，岩石不发生损伤，此时粘滞系数为定常数，且根据已有研究表明[16]，此时岩石并不出现加速蠕变破坏阶段。当超过损伤阀值时，岩石内部定常粘滞系数将会发生衰减，岩石也会出现黏弹性加速蠕变阶段。

损伤变量作为其中重要的中间参量，必须要进行公式化衡量表述，根据文献[17]定义的损伤方法及原理可知：

式中：0为岩石初始弹性模量，(,)某一时刻岩石变形模量，与加载应力和加载时间有关，根据文献[16,18]的研究，(,)可定义为：

(,)=0exp[-<-σ>/](7)

式中：σ为岩石长期强度值，长期强度可根据蠕变实验中等时曲线法确定，为岩石材料性质参数，其中<-σ>为双开关函数，即：

式（7）代入式（6）可得损伤变量为：

(,)=1-exp[-<-σ>/](9)

从上式可知，当应力低于长期强度值时，损伤为零；当应力超过长期强度时，岩石出现损伤，随应力增大，损伤更大，这与岩石破坏机制也是一致的。根据Kachanov有效应力概念，岩石在加载破坏过程中，应力会随着岩石破坏产生衰减，实质上加载应力是一种有效应力，并且给出了有效应力的表达式为[19,20]。

因而，对应于岩石加速蠕变阶段会产生有效应力，并且会产生粘滞系数的衰减，联立式（9）、（10）得：

考虑蠕变本构模型中的粘滞系数在损伤阶段的非定常性与蠕变加载过程中岩石损伤存在阀值特点，改进后的考虑损伤阀值效应的非定常性Abel黏壶元件本构方程为：

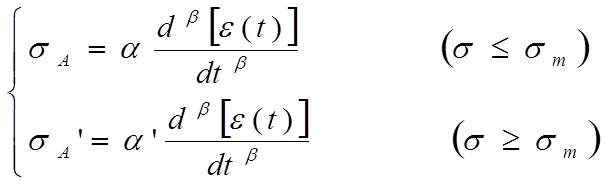
式中：σ指σ时，发生蠕变损伤时Abel黏壶元件中的有效应力。结合式（5）、（11）、（12）获得Abel黏壶元件损伤阀值以下与损伤阀值以上的方程为：

1.2 分数阶非定常蠕变模型的建立与求解

通常来说，岩石蠕变由初始减速蠕变、稳态蠕变、加速蠕变阶段组成。传统的蠕变本构模型主要是通过分别构建元件，组合成三元体，进而恰当的描述蠕变变形全过程。本文将采用弹性体元件表征初始减速蠕变变形ε；而初始减速蠕变与稳态蠕变阶段发生的黏弹性变形主要采用的是损伤阀值以下的Abel黏壶元件表述ε；在加速蠕变阶段发生的黏弹塑性变形则采用损伤阀值以上的非定常性Abel黏壶元件表述ε。

（1）当加载应力低于长期强度值时，即σ≤σ时，岩石不出现加速蠕变，蠕变变形只包含弹性变形与黏弹性变形两部分。弹性体元件由材料力学应力应变关系得：

式中：为岩石的弹性模量。

根据前文描述，表征粘弹性变形的为损伤阀值以下的Abel黏壶元件，其本构方程为：

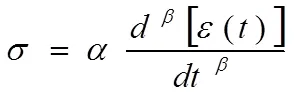
通过Laplace变换知解为[16]。

故而不出现蠕变损伤即不发生粘塑性变形之时，岩石蠕变本构方程为：

（2）当＞σ时，岩石将发生损伤作用，此时变形包括弹性变形、粘弹性变形及粘塑性变形，故而此时表征岩石粘塑性变形方程根据（13）式可写成：

对（18）式两边同时进行Laplace变换，得：

经由Laplace逆变换解得：

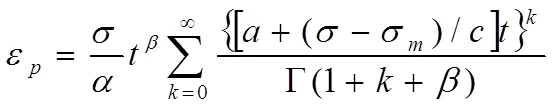
当发生蠕变损伤时，联立（17）（20）式得蠕变本构方程为：

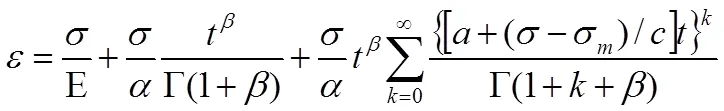
结合前述损伤阀值两种情况，构建出岩石损伤阀值下的非定常性分数阶蠕变本构模型为：

2 蠕变本构模型的验证

为了反演出模型中各个参数，采用双参数的Mittag-Leffler函数进行模型表述，其中该函数表达式为：

当参数=1时，Mittag-Leffler函数的一般形式可以总结为（24）式[21]。

带入式（22）中，可得＞σ时本构方程为：

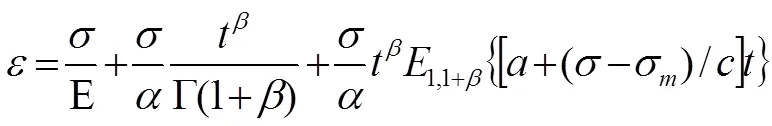
粒子群算法[22,23]由待定参数生成一系列未知变量，每个粒子均表示一个可能性解，根据定义范围确定所有解的先后顺序，最终确定最优解。为了反演出本文的蠕变本构模型，笔者基于Matlab编程技术，采用粒子群算法，对模型中参数进行反演求解，并搜索得到最优参数结果。

2.1 蠕变本构模型的拟合

笔者借助于沈明荣[24]红砂岩分级加载的试验结果，由过渡曲线法和等时应力应变曲线法确定该岩石长期强度为22.45 MPa。

（1）当≤σ时，取红砂岩第一级与第二级进行模型反演拟合，第一、二级加载应力分别为18.58 MPa、21.65 MPa，通过Matlab编程粒子群算法进行参数识别，得到的蠕变本构模型参数见表（1）。

（2）当＞σ时，蠕变损伤阈值触发并发生粘塑性变形，取红砂岩第四级与第六级进行参数反演拟合，第四级与第六级加载应力分别为26.8 MPa、27.2 MPa，参数反演拟合结果见表（1）。

表1 蠕变本构模型拟合参数

从表（1）来看，本文所建立的岩石损伤阀值效应下的非定常分数阶蠕变本构模型良好的模拟出蠕变三阶段，特别是在非线性加速蠕变阶段，与实验数据吻合程度高，且本文在所用模型参数并没有增多的情况下考虑到蠕变损伤的时效作用对粘滞系数的影响，在工程应用中更具有应用价值，由拟合结果精度可知，本文模型误差较小，此亦论证了该模型的适用性与有效性。

2.2 参数敏感性

根据该模型中参数可知，加载应力与求导阶数是影响模型结果的重要变量。加载应力所处于的范围，关乎到损伤阀值的触发，进而影响本构模型应用的合理性。因而，本文对上述两变量进行参数敏感性分析。

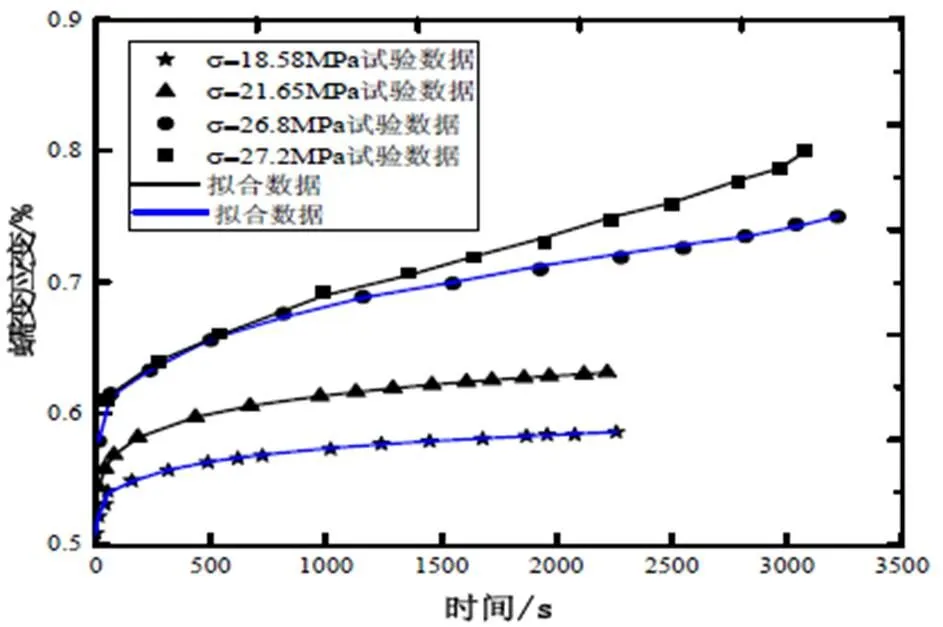
图1 实验数据-本文模型对比

针对本构模型，保留本构模型中除加载应力以外的所有参数，将加载应力取一组不同的数值，得到加载应力的一簇曲线。该曲线表征了不同加载应力水平下的本构模型。从图2可看出，随着加载应力水平的增大，蠕变应变量值逐渐增大，但是蠕变曲线的走向并没有发生较大改变，表明加载应力的增大或下降，只影响蠕变变形量，并不影响蠕变速率。

图 2 加载应力敏感度

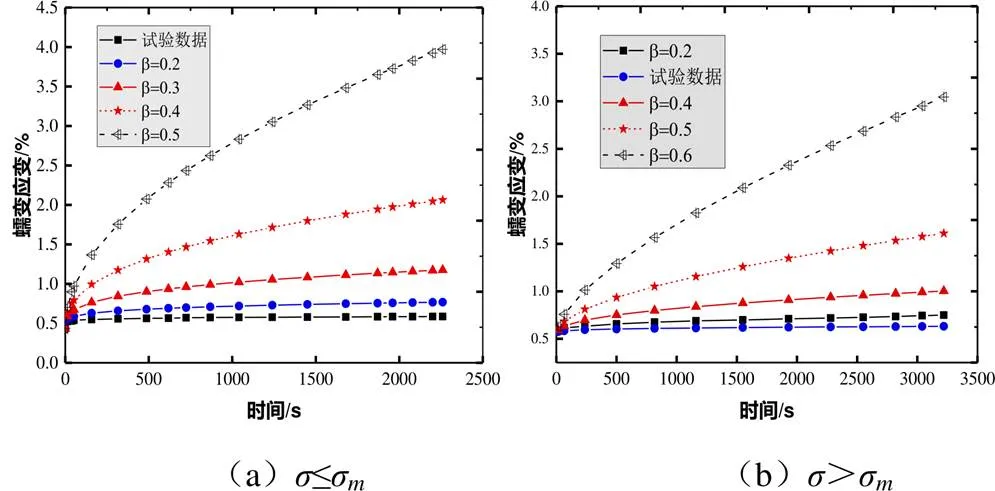
图 3 求导阶敏感度

同理，保留本构模型中除求导阶数以外的所有参数，改变求导阶数取值，得到不同求导阶数的一簇曲线。从图3可看出，当求导阶数愈大时蠕变曲线走向均有显著改变，蠕变速率发生较大的变动，求导阶数愈大，蠕变速率愈大，表征了求导阶数反映了岩石蠕变速率。

3 结 论

本文从损伤的阀值效应出发，通过改进经典模型，建立考虑岩石损伤效应下的模型元件，构建出考虑岩石实际损伤状态的蠕变本构模型。主要结论如下：

（1）基于分数阶微积分理论，对Abel黏壶元件进行改进，得到表征损伤阀值效应的非定常性元件模型，基于经典元件组合理论，通过一个弹性体、Abel黏壶元件以及改进后的考虑损伤阀值触发作用的Abel黏壶元件建立了一个新的岩石蠕变本构模型，并论证该模型适用于岩石加速蠕变阶段；

（2）通过与实验数据的反演拟合，结果表明，建立的岩石蠕变本构模型能良好的表征岩石蠕变三阶段，特别是非线性加速蠕变阶段，与实验数据相关程度高，误差较小，且该模型考虑的损伤阈值触发作用情况更贴切岩石蠕变行为；

（3）通过对本构模型中加载应力及求导阶数敏感度分析，获得了影响蠕变应变量的参数为加载应力，影响蠕变速率的为求导阶数。从本构模型上揭示了影响岩石蠕变行为特性的基本参数。

[1]孙钧.岩土材料流变及其工程应用[M].北京:中国建筑工业出版社,1999

[2]王晓波,万玲.考虑损伤的岩石非线性蠕变模型[J].科学技术与工程,2016,16(20):1-5

[3]周新,巨能攀,赵建军,等.片岩三轴蠕变特性及蠕变模型研究[J].科学技术与工程,2015,15(33):218-223

[4]蒲少云,黄质宏,饶军英,等.低动应力下岩石分数阶Burgens本构模型[J].长江科学院院报,2018,35(2):109-115

[5]He ZL, Dai B. Secondary Development of a Nonlinear Creep Model Based on Fractional Derivative in FLAC3D[C]// 2018 11th International Conference on Intelligent Computation Technology and Automation (ICICTA). IEEE Computer Society, 2018

[6]何志磊,朱珍德,朱明礼,等.基于分数阶导数的非定常蠕变本构模型研究[J].岩土力学,2016,37(3):737-775

[7]何志磊,朱珍德,李志敬.大理岩结构面非线性蠕变损伤本构模型研究[J].科学与技术与工程,2014,14(32):68-72

[8]陈卫忠,王者超,伍国军,等.盐岩非线性蠕变损伤本构模型及其工程应用[J].岩石力学与工程学报,2007,26(3):467-472

[9]吴斐,谢和平,刘建锋,等.分数阶黏弹塑性蠕变模型试验研究[J].岩石力学与工程学报,2014,33(5):964-970

[10]吴斐,刘建锋,武志德,等.盐岩的分数阶非线性蠕变本构模型[J].岩土力学,2014,35(增2):162-167

[11]苏腾,周宏伟,赵家巍,等.基于变阶分数阶导数的岩石蠕变模型[J].岩石力学与工程学报,2019,38(7):1355-1363

[12]蔡煜,曹平.基于Burgers模型考虑损伤的非定常岩石蠕变模型[J].岩土力学,2016,37(S2):369-374

[13]Kilbas AA, Srivastava HM, Trujillo JJ. Theory and Applications of Fractional Differential Equations [M]//North-Holland Mathematics Studies. Amsterdam: Elsevier Science Ltd., 2006

[14]殷德顺,任俊娟,和成亮,等.一种新的岩土流变模型元件[J].岩石力学与工程学报,2007,26(9):1899-1903

[15]周宏伟,王春萍,段志强,等.基于分数阶导数的盐岩流变本构模型[J].中国科学:物理学力学天文学,2012,42(3):310-318

[16]宋勇军,雷胜友.基于分数阶微积分的岩石非线性蠕变损伤力学模型[J].地下空间与工程学报,2013,9(1):91-95

[17]杨百存,薛雷,王苗苗,等.基于能量原理的页岩损伤破裂研究[J].应用基础与工程科学学报,2018,26(5):997-1004

[18]刘保国,崔少东.泥岩蠕变损伤试验研究[J].岩石力学与工程学报,2010,29(10):2127-2133

[19]唐皓,李强,王东坡,等.基于分数阶微积分及改进弹塑性体的流变模型[J].防灾减灾工程学报,2016,36(6):978-983

[20]Kachanov M. Effective elastic properties of cracked solids: Critical Review of Some Basic concepts [J]. Applied Mechanics Review, 1992,45(8):304-335

[21]陈小磊.分数阶理论在BP神经网络中的应用[D].南京:南京林业大学,2013:43-45

[22]熊雪强.分级循环加卸载砂岩蠕变声发射特性研究[D].赣州:江西理工大学,2012:51-58

[23]苏国韶,冯夏庭.基于粒子群优化算法的高地应力条件下硬岩本构模型的参数辨识[J].岩石力学与工程学报2005,24(17):3029-3034

[24]沈明荣,谌洪菊.红砂岩长期强度特性的试验研究[J].岩土力学,2011,32(11):3301-3305

Non-steady State Creep Constitutive Model of Rock Based on Fractional Calculus

LI Na, YU Xiao-yao

476000,

Based on fractional calculus theory, the commonly used Abel clay pot element in rock creep constitutive model is improved, and the unsteady element model representing damage threshold effect is obtained. It is proved that the model can be well applied to rock creep stage. Based on the classical component combination theory, a new constitutive model of rock creep is established by using elastomer, Abel clay pot and Abel clay pot element triggered by improved damage threshold. Based on the inversion and fitting of experimental data, the results show that the creep constitutive model can well characterize the three stages of rock creep, especially the non-linear accelerated creep stage. It has high correlation with experimental data and small error. Moreover, the damage threshold triggering effect considered by the model is more suitable for rock creep behavior. Through the sensitivity analysis of loading stress and derivative order in the constitutive model, the parameters affecting creep strain are obtained as loading stress and creep rate as derivative order. The basic parameters affecting creep behavior of rock are revealed from the constitutive model.

Rock creep; fractional calculus; constitutive model

TU45

A

1000-2324(2021)02-0288-05

10.3969/j.issn.1000-2324.2021.02.023

2019-02-14

2019-04-07

河南省高等学校重点科研项目(17A120012)

李娜(1984-),女,硕士,讲师,研究方向:微分方程数值解. E-mail:lgdlina@163.com

网络首发:http://www.cnki.net