论小学数学教学中数形结合思想的应用
⦿王柳柳
“数”与“形”有着千丝万缕的联系,运用“数”研究“形”可更加精确地掌握“形”。运用“形”研究“数”则能更加直观地体现“数”的规律。在教学中培养学生的数形结合思想,对提升学生的解题能力,促进其以后更好的学习数学知识具有重要的现实意义。
一、用于解答分数习题
分数加法是小学数学的重点知识。教学中为深化学生对分数的理解,提高学生分数运算能力,应结合数形结合思想为学生讲解如下习题的解答:

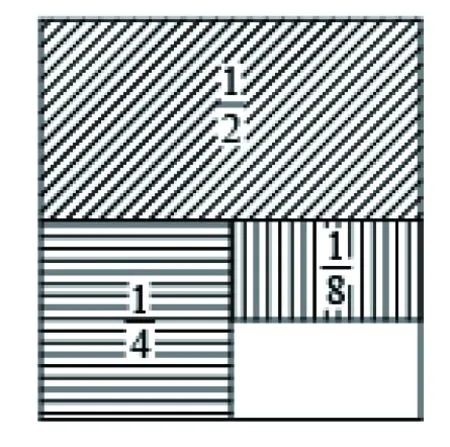
图1

二、用于解答图形与位置习题
图形与位置是小学数学的重要构成部分。通过该部分知识的讲解可使学生运用数准确地定位位置。教学中注重为学生讲解如下例题,使学生认识到运用数还可计算图形的面积,进一步拓宽学生视野。
例2,如图2一个平行四边形ABCD,它的三个顶点已经用数对表示,点D的数对表示的是____,平行四边形ABCD的面积为____。

图2
该题目中数的规律使用图形进行表示,非常直观。认真观察图中B、C对应的数对,可知B和C数对的第二个数一样,第一个数之差应表示平行四边形的边长6-2=4,由平行四边形知识可知A、D对应的数对也应满足此规律,则D的第一个数应为4+4=8,第二个数应为6,即D对应的数对为(8,6)。平行四边形的面积是底乘高,根据图中内容可知A与B、C与D数对的第二个数表示其高,即,6-3=3,则平行四边形的面积S=4×3=12。
三、用于解答数的运算习题
数的运算是小学数学的重要知识点,尤其小数的乘法运算需要学生牢固掌握、熟练应用相关法则。教学中为提高学生小数乘法运算能力,提高相关问题解题技巧,围绕经典习题,向学生展示运用数形结合思想解题的过程,使其体会数形结合思想在解题中的便利,提高其在解题中的应用意识。
例3,两个小数相乘,如果一个因数增加4,积就增加14.4,如果一个因数减少2,积就减少5,那么这两个因数原来分别为____和____,原来的积为____。
将小数转化为矩形的边,将乘积使用矩形的面积进行表示,可大大提高解题效率。两个因数相乘可联想矩形的面积计算公式,运用数形结合思想进行求解。一个因数增加4,积就增加14.4,如图3所示,可清晰地看到原来矩形的长对应其中一个因数,即,14.4÷4=3.6。

图3
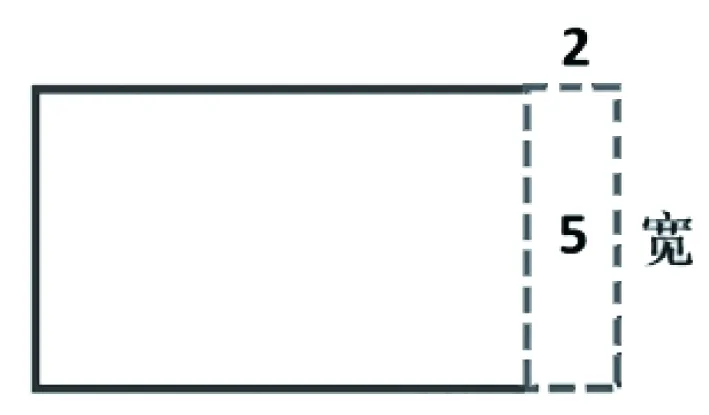
图4

图5
如果一个因数减少2,积就减少5,如图4所示,可看到原矩形的宽为5÷2=2.5,因此,这两个因数分别为3.6、2.5,则原来两个因数的积为3.6×2.5=9。
四、用于解答圆柱与圆锥习题
圆柱与圆锥在小学数学中占有重要地位。相关题型复杂多变,部分习题难度较大,需要学生具备良好的空间想象能力,绘制出正确的图形,运用所学知识进行解答。教学中可创设新颖的问题情境,鼓励学生运用数形结合思想进行分析,不断提高学生运用数形结合思想解题的灵活性。
例4,一直角梯形的上底为2厘米,下底为4厘米,高为6厘米,以它的上底为轴旋转一周,形成一个图形,求这个图形的体积是多少立方厘米(π取3.14)?
该题目考查图形的旋转、圆柱体、圆锥体体积的计算知识,对学生的空间想象能力要求较高。其中正确的绘制出对应的图形是解题的关键。授课中可给学生留下一定空白,要求学生根据自己的理解,尝试着绘制相关图形。根据题意绘制如图5所示的图形:
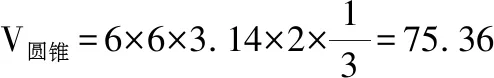
五、总结
小学数学教学中为提高学生的解题能力,既要注重基础知识讲解,使学生深入理解数学知识本质,又要注重向学生灌注相关数学思想。其中数形结合思想在解题中应用广泛,为使学生灵活运用解题中,教学中应围绕具体习题,认真讲解数形结合思想的具体应用,使其学生掌握运用数形结合思想解题的思路与细节,不断提高应用水平。

