基于主要成分分析的人脸二维码识别系统

王向豪，谢钧霖，曾凡馨，姚西成

（西南石油大学理学院，成都610000）

0 引言

这个高速发展的时代，一切事物都将与“快”相联系。人脸识别技术的发展成熟保证了人们的信息安全，二维码的飞速发展成为了现如今信息传递的新媒介。“慢”就会被淘汰，因此减少现如今人脸识别过程的时间仍是目前研究的一个课题。本文将现今两项比较前沿的领域——人脸识别和二维码，融合在一起，以达到快速识别人脸信息的目的。

其中，人脸识别技术的优点在于：①图像采集方式灵活、方便，通过手机、相机等设备就能完成；②图像的采集过程简单；③人脸图像信息易于处理；④人脸面部特征易于提取和识别。QR 二维码的优点在于：①QR码的可存储信息量大；②技术简单便于实现。本文将这两项前沿技术相结合，有望为人脸识别技术未来的发展提供一个新的思路。

1 人脸图像信息处理

1.1 主成分分析PCA

主成分分析（Principal Component Analysis）是一种应用非常广泛的基础数学分析方法。其内在思想是K-L 变换或者霍特林变换，通过分析变量找出一组最优正交基，使得变换后的变量与原来变量之间的均方误差最小。通过K-L 变换后，将原来的自变量变换成另一组变量，变换后的变量便是“主成分”。从“主成分”中提取一部分重要成分作为新的自变量，最后用最小二乘法对选取主成分后的模型参数进行估计。

PCA 原理是将一个高维向量通过一个特征变换矩阵将变换后的变量投影到一个低维向量空间中形成一个低维向量，并且几乎不损失主要信息。本文的人脸识别过程中，将每一个特征脸处理成了一个特征脸。

PCA 算法经过多年的发展和研究已经非常完善和成熟，因此本文将直接应用MATLAB 本身的PCA 算法将ORL 人脸库的数据信息进行降维处理，得到的特征脸信息再与QR 二维码技术结合，设计出基于主成分分析的人脸二维码识别系统。

1.2 PCA人脸压缩与重构算法分析

本文的训练集以及测试集采用的是ORL 人脸库。基于ORL 人脸库的信息多样和标准灰度图像的优点，我们将直接对选取的人脸样本集进行训练。从ORL 人脸库中选取380 张人脸图像，每张图像的像素为112×92，为了方便数据处理我们将每张图像放缩成像素为64×64 的图像。

图1 所示的图像为放缩后的图像，可以看出经过放缩后的图像仍然可以完全识别，而且没有损失主要的特征信息。

图1 放缩前后的图像

通过放缩后的人脸图像矩阵为Ai=R64×64，其中每个图像矩阵按照64×64 的列向量进行重新排列，构成一个样本训练集φ=[φ1,φ2,…,φ380]，φi表示长度为64×64 的列向量。

图2 图像压缩成向量示意图

样本训练集构成后我们将获取平均脸，平均脸在数学意义中表示为样本训练集的平均值，为同时平均值mφ也为样本集所有人脸图像共有的特征成分。

将得到的平均脸放缩成像素为64×64 的人脸图像，如图3 所示。

图3 平均脸图像

因为我们需要训练集样本中图像彼此不同的部分，因此需要将训练集中的共有成分去掉，即X=[x1,x2,…,x380]，其中xi=φi-mφ。

接着求出协方差矩阵的特征值λi和对应的特征向量ui。本文对于求协方差矩阵的特征向量和特征值使用的是MATLAB 自带的PCA 算法，通过MATLAB自带的PCA 算法计算出的特征值和特征向量经过测试得到的结果可以正确地识别测试图像。

将协方差矩阵的特征值进行降序排列，即：

经过多次测试，我们取n=350 时得到的测试相对误差最小，即大于λ350的特征值对应的特征向量构成主成分，因此主成分构成的变换矩阵为：

这样每一幅人脸都可投影到Ueig=[u1,u2,…,u350]构成的特征脸子空间中，任何一幅人脸图像都可以向其作投影y=xUeig T，得到一组经变换后的变量，即低维向量y，此低维向量可作为人脸识别的依据。

计算出特征脸子空间后，我们便可以将被识别人脸图像向其投影。首先将被识别人脸图像压缩成向量，然后将其共有的成分剔除。即：

其中xs为被识别人脸图像的特有成分，φs为被识别人脸图像的全部信息，mφ为训练集样本平均值或者平均脸信息。

将被识别的人脸图像的特有成分经过特征变换矩阵投影后，便得到了降维后的向量ys，此向量也称为被识别人脸图像的“主成分”。即：降维后我们需要再对主成分进行人脸图像重构，因为K-L 变换是正交对称性的，因此Ueig

-1=Ueig T，即：

其中E为单位矩阵，因此xs=ysUeig，再将得到的被识别人脸图像的特有成分加上平均脸，即φs=xs+mφ，重构出被识别的人脸图像。

Java 是现如今实现QR 二维码生成与信息识别的主流工具，因此在提取被识别人脸图像的主成分后，我们将使用Java 来实现将此主成分的信息转换成QR 二维码，进而再对QR 二维码信息提取并对人脸图像的重构，以达到对人脸信息的快速识别的目的。

2 二维码转换以及识别

2.1 QR码

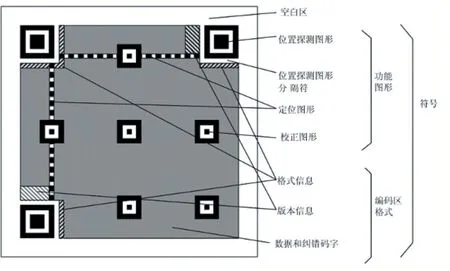
图4 二维码图形格式

QR 码（Quick Response）是一种矩阵式二维码符号。QR 码有制作成本低、存储容量大、应用和储存范围广、可靠性高等特点。QR 码可以同时在水平和垂直方向的二维空间储存信息，在表示信息方面也可以记载更复杂的数据，除了字母和数字外还可以录入汉字、图片、指纹、网址等信息，相当一个可移动的数据库。而相比其他二维码而言，QR 二维码具有识读速度快、数据密度大、占用空间小的优势。结合QR 二维码以上优势，它能够储存大量人脸信息，制作成本低，并且能够快速识别，所以本文采用QR 二维码来对人脸信息进行储存。

2.2 将人脸图像生成二维码

MATLAB 本身不具备生成和识别二维码的函数，所以需要借助Java 的ZXing 开源库，之后再使用MAT⁃LAB 提供的用于和Java 模块通信的各种函数。为了生成二维码。首先创建一个ZXing.MultiFormatWriter的实例，从而把抽象的Java 类实例出个体，实例对象才能直接进行交互。接下来，使用MultiFormatWriter 的encode 方法，对之前导入的人脸数据信息进行编码。至此，编码就已经完成。下一步要做的，是从我们创建的BitMatrix 实例中提取图像数据，用它的ToBitmap 将其转化为一个dotNET 的Bitmap 对象，然后再将其转化成MATLAB 矩阵。在这过程中需要将像素之间空格和换行符删除，从而将字符串转换为MATLAB 可以接受的图像矩阵。最终生成的包含人脸数据信息的二维码示例如图5。

图5 含有主成分信息的二维码

2.3 二维码的识别与图像还原

识别QR 二维码，需要用到的类主要是BinaryBit⁃map，识别过程关键类是QRCodeReader。通过指令查阅类可知，所用到的函数输入变量类型是BinaryBit⁃map，所以就要求解码之前要进行类型转换，即将普通格式的二维码图片转化为Java 类型图像格式，之后就可以调用函数对Java 类型图像灰度化、降噪、边缘检测、轮廓提取、矫正畸变，最终得到二维码中的人脸信息（向量数据）。

将二维码主要信息提取后，我们再利用K-L 变换是正交对称性：U-1=UT，即：UUT=E，其中E为单位矩阵，U为特征脸子空间。因此我们再将从二维码中提取的信息乘以特征脸子空间，即xs=ysU，得到被识别人脸图像的特有成分后，我们再将得到的被识别人脸图像的特有成分加上平均脸，即φs=xs+mφ，重构出被识别的人脸图像。

图6 原始图像以及重构图像及误差率

从图6 中可以看出，被识别的人脸图像可以很好地被重构出来，而且并没有产生明显的失真。同时重构前后的数据均在误差允许的范围之内，因此我们的人脸识别系统已经基本完成，且具有很高的可靠性。

3 结语

本文是将当前较为热门的两个领域结合，人脸识别和QR 二维码结合在一起，将人脸图像信息录入二维码中，可以通过扫描二维码迅速识别出人脸信息。本文实现了人脸图像信息处理、QR 二维码的生成及识别，虽然二维码有着识别快、存储信息量大等优点，但是通过二维码能够快速识别出人脸信息的同时，也存在信息泄露的风险，可以在当前研究的基础上进一步提高二维码的加密性和安全性，对人脸识别系统我们还需要更加完善的措施，以保证二维码内信息的安全。

目前能够识别QR 二维码的设备有限，二维码的识别设备大部分是手机和平板等手持电子设备，因此，下一步的研究可以将PC 端转换到Android 平台或者iOS 平台上。