基于深度强化学习的无人驾驶优化评价方法
李文韬,谢小红,孙晓燕
(1.广西水利电力职业技术学院,公共基础部,南宁530023;2.广西财经学院,新闻与文化传播学院,南宁530003;3.广西财经学院,管理科学与工程学院,南宁530003)
0 引言
近年来,随着人工智能的不断发展,智能手机、智能声控系统以及无人驾驶逐渐步入人们的生活。人工智能带来的不仅仅是生活方式与工作方式的便捷,更是划时代的产物,标志着人类进入智能时代。当前,无人驾驶正在进行广泛的推广,如何对未知复杂动态环境具备自动避障功能[1],同时还要兼具稳定性和泛化能力已成为无人驾驶领域的热门课题。而强化学习对复杂环境的适应性,成为了无人驾驶的重要研究方法。
强化学习(Reinforcement Learning,RL)是人工智能中的一种重要学习方法,其采用试错的方式进行训练,并得出最优的行为策略[2]。目前,强化学习已被广泛应用于手工业制造[3]、优化与调度[4]、机器人控制[5]、模拟仿真[6],以及游戏博弈[7]等领域。强化学习的主要思想是由实验智能体(agent)在模拟环境中累计得到的奖励值,根据奖励值训练得到目标的最优策略[8]。因此,强化学习主要侧重于完成高维度非线性的函数逼近和多维特征的策略学习问题。
随着深度学习(Deep Learning,DL)[2]逐渐成为机器学习领域中的重要发展方向。深度学习已被广泛应用于图像处理、语音识别以及自然语言处理等领域,并取得了重大的突破[9]。深度学习最重要的特性是能够自动寻找到高维数据(如图像、文本、声音等)的低维表征,通过将归纳偏置值(Inductive bias)引入到分层卷积神经网络架构中,使机器学习研究者很好地解决了高维度的问题。深度学习出现的同时也推进了强化学习的发展,通过将深度学习和强化学习两种学习模式组合,形成深度强化学习(Deep Reinforcement Learning,DRL)这一新领域[10]。深度强化学习通过利用两种学习模式各自的优势,处理决策问题中的高维状态空间与离散或连续动作空间。
在深度强化学习取得的成果中,已有许多达到甚至赶超人类的先进水平。Mnih 等人[11]结合深度学习和Q-learning 算法,提出了深度Q 网络(Deep Q Network,DQN)算法,在一定程度上解决了非线性函数计算的不稳定性问题。Chae 等人[12]通过DQN 对无人驾驶展开了研究,并将动作划分为无、轻、中以及强的四种制动,设计了防碰撞的奖励函数来达到防止过早或过迟制动,结果表明,车辆基本实现了自主刹车。杨顺等人[13]提出了一种基于多类型传感数据训练自动驾驶策略的方法,在TORCS 中进行了仿真模拟,在车速和车辆横向偏移的控制中取得了不错的效果。Xie 等人[14]提出了一个新的学习框架——辅助深度确定性策略梯度算法(Assisted Deep Deterministic Policy Gradient,AsDDPG),此算法使无人驾驶汽车避障训练的速度更快,对DRL 网络结构的敏感性更低,并且始终优于标准的深度确定性策略梯度网络。尽管以上研究都取得了不错的成果,但仍存在以下一些问题:①由于评价网络的一体化,容易产生一些无用动作,寻找最优动作难度较大,导致学习效率低。②学习训练效率不高,智能体需要和环境进行多次试错以获得大量样本数据后才能放入神经网络中迭代获得最优解。由于网络参数在训练前是随机的,初始值与最优策略存在较大的差距,需要经过较长的时间才能收敛。
本文借鉴了深度确定性策略梯度(Deep Determin⁃istic Policy Gradient,DDPG)[15]算法具有连续动作空间、收敛速度快的优点,提出了一种基于DDPG 算法的优化评价改进算法,目的是进一步提高算法的性能。
1 技术背景
1.1 强化学习
强化学习[16]又称试错学习,是智能体和环境之间通过交互,使智能体获得最大的奖励。强化学习原理如图1 所示。
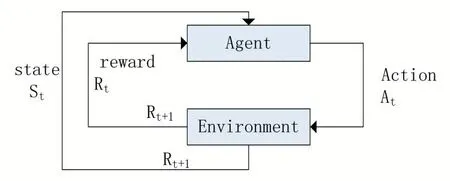
图1 强化学习原理图
在RL 中,Agent 根据当前的状态St选择一个动作At使环境发生变化,并从中获得Rt且改变当前状态,Agent 再根据获得的状态选择一个使其奖励最大的动作A。采用马尔科夫决策过程(Markov decision pro⁃cess,MDP)可以对RL 进行建模。马尔科夫决策过程可以定义为:(S,A,P,R,γ),其中S表示状态空间;A表示动作空间;P代表下一状态的迁移概率,Pa(s,s' )=Pa(s'|s,a)为一个条件概率,代表Agent 在状态s和动作a下,到达状态s’的概率;R代表奖励函数,Ra(s,s')则是一个激励函数,是Agent 在动作a下从状态s到状态s’所获得的奖励;γ为折扣因子,γ∈( 0,1] 。
Agent 所执行的动作由策略π 定义,策略π :S→A是从状态到动作空间的映射。表示状态st选择动作at,并以概率函数f(s,at)获得下一状态st+1,同时得到环境反馈量化奖励rt。
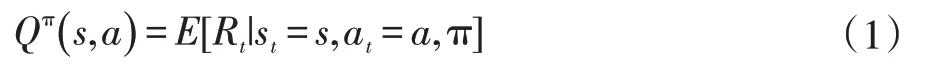
状态动作值函数Qπ(s,a)表示在st下执行at,并遵循策略π 所获得的累积回报表示为:当策略π*的期望回报大于或者等于其他所有策略期望汇报时,π*成为最优策略,它们有同一个状态动作值函数:
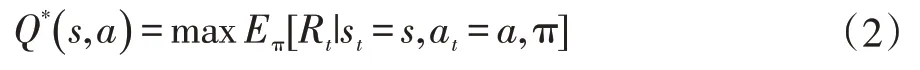
该式也成为最有状态动作值函数,它遵循贝尔曼方程,即:
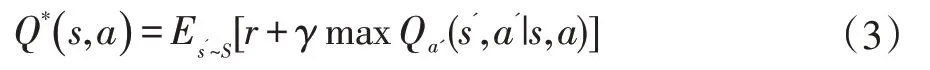
根据传统的强化学习,往往是经过不断迭代贝尔曼方程求解状态动作函数,但仅局限于解决具有离散动作空间的问题。针对强化学习的这一缺陷,一般使用线性函数逼近器近似表达状态动作值函数,即Q(s,a|θ)≈Q*(s,a),但在状态空间较大时,很难找到最优解。因此大部分研究者开始用深度神经网络来求解并展示值函数或策略,深度强化学习也就应运而生。
1.2 DDPG算法
DDPG 是2015 年Deep Mind 在确定性策略梯度算法(Deterministic Policy Gradient,DPG)的基础上改进的一种深度强化学习算法。该算法是在Actor-Critic 方法的本质上结合了DQN 的经验回放和双网络结构方法对DPG 的改进。
Actor-Critic 算法的模型主要由Actor 网络和Crit⁃ic 网络组成。如图2 所示。
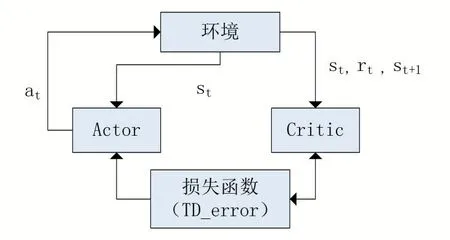
图2 Actor-Critic结构
Actor 网络的输入是st,通过网络后输出动作at,环境执行动作at获得下一状态st+1,再将st,rt、st+1输入到Critic 网络。再通过时序差分方法得出TD_error,之后再重新调整Critic 的网络参数。由于Actor-Critic算法的输出是随机选择的动作,将运算出选择此动作的概率并用对数表示。概率对数和TD_error 的乘积就是Actor 网络的损失函数。
经验回放指的是在Agent 学习前,将探索到的经验储存到经验池中。在学习过程中,Agent 从检验缓存池中随机采样训练神经网络,消除连续数据相关性,同时能够提高样本利用率。在Agent 在与环境交互过程所获得的经验样本中,不同的经验样本对神经网络的训练所起作用大不相同。因此也存在一些不可忽略的问题,例如随机抽取经验样本的质量不能够有很好的保障,从而导致训练效率低,收敛速度慢。所以需要用到双网络结构来缓解问题。
双网络结构是建立两个神经网络结构一样而参数不一样的方法。其分为评价网络(eval net)和目标网络(target net)。评价网络主要是对目标网络间歇性的更新网络参数,目标网络主要是构建出目标Q值(tar⁃get_Q)和评价网络构建出估计Q值(eval_Q)。再使用时间差分法(TD):
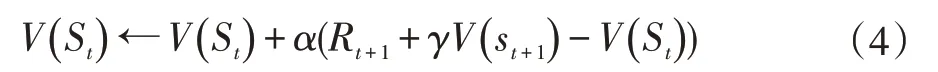
计算出目标Q值和估计Q值的差,即TD_error。Critic 网络的损失函数就是使用经验样本的均方误差方法。但也存在以下问题:对较高动作维度的连续控制不均衡和训练效率不高的问题。DDPG 算法结构如图3所示。
2 优化评价的DDPG算法
本文在DDPG 的基础上改进损失函数并引入Dropout,将网络中一些次优的神经网络单元暂时丢弃,使最优动作与次优动作拉开差距,进而提高训练的效率。
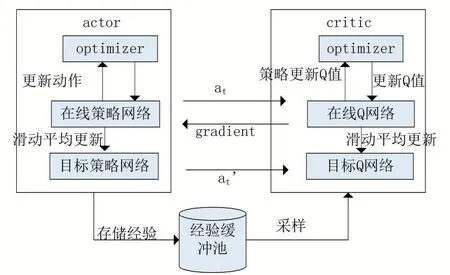
图3 DDPG算法结构图
2.1 改进的损失函数
在DDPG 算法中,由于评价网络评价的一体化,容易出现产生一些无用动作,寻找最优动作难度较大导致学习效率较低的问题。损失函数主要是用来表达网络的预测值和真实值之间的相近关系。本文提出改进损失函数,使选择的动作之间存在最优和无效的区别,Critic 网络能够更好地来评估动作,进而提高模型的鲁棒性。
DDPG 算法通常使用的损失函数是均方误差:

其中target_Q 为目标Q 值,eval_Q 为评估Q 值,在求和平均后所获得的最优动作与次优动作无法拉开差距,难以做出良好的评价,主要是将动作维度替换取平均,拉开最优动作与次优动作之间无法拉开距离,表达式如下:
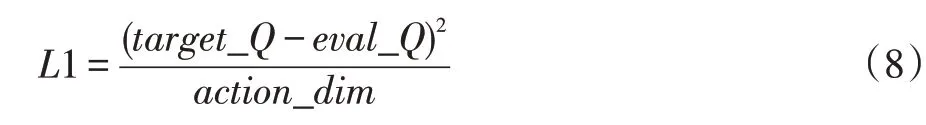
其中target_Q 和eval_Q 的差值是TD_error,TD_error 的平方再对action_dim 取整可以对action 做到优化评价。换而言之,Agent 在学习一段时间后选择动作的部分差值会变小,而动作差值越大在经验池中占有的比例也越大。在Critic 网络测试动作的好与坏的过程中,次优动作的差值相比较大,对神经网络的参数的影响也就加大了。算法根据所有的动作分布做了动作评估,扩大了最优动作与其他动作的TD_error 差距,也提高了算法收敛速度。
虽然公式(8)能够对最优动作和无效动作做出良好的评价,但是在同数值的情况下2×target_Q×eval_Q是明显大于target_Q2和eval_Q2,因此本文在公式(8)的基础上进行改进,表达式如下:
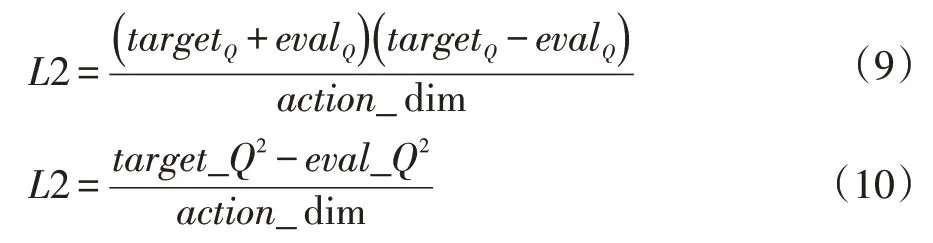
其中target_Q2和eval_Q2的差值要大于完全平方的,虽然Loss 的值会变大,但这也使得最优动作与次优动作的距离拉开,使评价网络更好地对动作进行优化评价。
2.2 引入Dropout
在深度学习中神经网络训练时经常出现网络过拟合的问题,而Dropout 是一种可以有效缓解这一现象的正则化方法。在网络训练的过程中,将神经网络单元从训练模型中有概率性的暂时去掉。前向传播公式如下:

其中,r(l)服从伯努利分布概率为p,y(l)为第l 层的激活值,y~(l)为第l 层的输出值,为第l+1 层的权重,为隐藏层的输入,f(∙)为激活函数。由于在使用随机样本进行训练网络时,会让网络进入往次优动作方向学习,从而导致网络弥乱,本文引入Dropout 能够缓解经验缓冲池的随机采样。使用Dropout 时会将网络中一些次优的神经网络单元暂时丢弃,为了不让较优的神经元丢失,选择神经元置零的概率为0.3。本文在Critic 网络的最后一层全连接层后引入Dropout,对于神经网络而言,其性能得以提高,并且各个网络参数共享又互相独立,减少特定神经元之间的协同作用,使每个神经元的提取更加具有鲁棒性。
2.3 OE-DDPG算法
OE-DDPG 算法是将改进的损失函数和引入的Dropout 机制相结合。其主要作用是利用改进损失函数把最优动作和次优动作的TD_error 差距进行区分,再引入Dropout 机制放弃一些的神经网络参数使得eval_Q 的值更小,可以更有效地利用经验缓冲池中抽取的随机经验样本,能够让Critic 网络更好地评估动作,进而提高算法的收敛速度。本文提出的OE-DDPG算法伪代码如下:

3 无人驾驶汽车模拟仿真
3.1 仿真环境
为了验证方法的有效性,我们在多种环境下进行了测试,搭建了简单、中等和复杂的模拟仿真环境对无人驾驶汽车进行方法验证。在仿真中,使用Python 库中的Pyglet 模块模拟构建2D 无人驾驶汽车环境,其中包含了连续的动作空间,5 个感应器,可以使小车进行前进、左微转弯、右微转弯、左转弯和右转弯的操作。动机与动作映射关系见表1 所示。
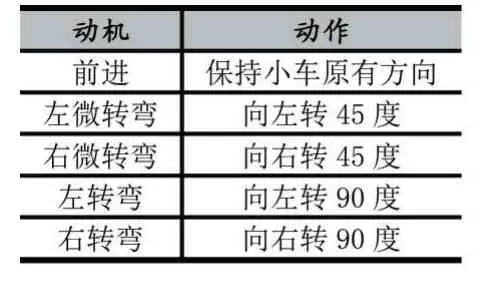
表1 无人驾驶汽车动机与动作映射表
本文利用OE-DDPG 算法仿真无人驾驶汽车在三种不同的环境下的障碍物规避实验。每一种环境下有不同数量的障碍物,分为简单、中等和复杂三种实验环境。无人驾驶汽车模拟仿真区域大小为500×500,目标无人驾驶汽车大小为20×20。在模拟仿真的过程中,如果无人驾驶汽车在模拟环境内没有碰撞障碍物并能够回到原点视为完成任务,若碰撞到障碍物则需要重新开始。本文设计三种不同无人驾驶汽车环境进行比较模拟仿真,如图4 所示。
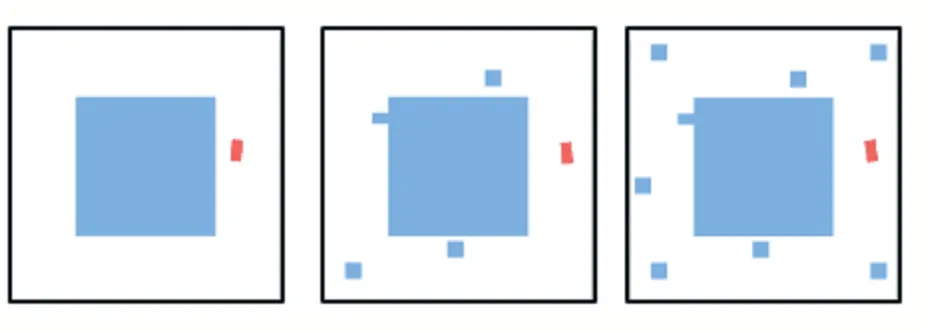
图4 三种不同仿真环境
为保证仿真实验的公平性,三种环境中的参数保持相同,其中经验缓冲池大小为2000,批次选取样本数量为16,最大情节为500,每情节最大时间步数为300,折扣因子γ为0.9,Actor 网络学习率为1×10-4,Critic网络学习率为1×10-3。
3.2 仿真结果及分析
OE-DDPG 算法是通过改进损失函数并加入Drop⁃out 机制相结合。为区分算法的名称,我们将原始DDPG 算法加入Dropout 机制得到的算法称为OE1-DDPG,将仅改进损失函数得到的算法称之为OE2-DDPG。
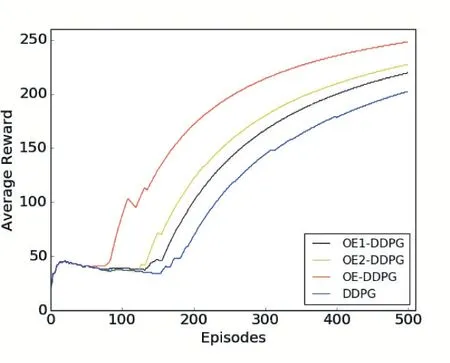
图5 简单环境算法比较
如图5 所示,OE-DDPG 算法在简单环境下与算法OE1-DDPG 和算法OE2-DDPG 及原始DDPG 的性能对比。在模拟环境中,由于前50 代是累计缓冲经验池,所以获取奖励基本重合。在50 代后网络模型进行学习,OE-DDPG 算法学习的效率明显高于其他算法。而原始DDPG 的学习效率比较低,大约在150 代才开始学习,显然收敛速度不好。OE-DDPG 算法在学习效率和收敛速度效果上均优于原始DDPG 算法。
在中等环境下的算法性能对比,如图6 所示。是在模拟环境中,100 代到250 代之间算法OE2-DDPG效果优于其他两个算法,缺点是学习速率缓慢。OEDDPG 算法在开始进行网络学习时没有快速的对最优动作进行优化,但是在学习速率和收敛速度上效果是优于其他两个算法的。从曲线可以看出OE-DDPG 算法在碰到障碍物时能够及时地做出调整,OE1-DDPG算法使用的均方误差在学习速率和最优动作的优化上都逊色于OE-DDPG 算法。前120 代两个算法学习的速率都不高,但是OE-DDPG 算法的比较平滑,无梯度消失问题。
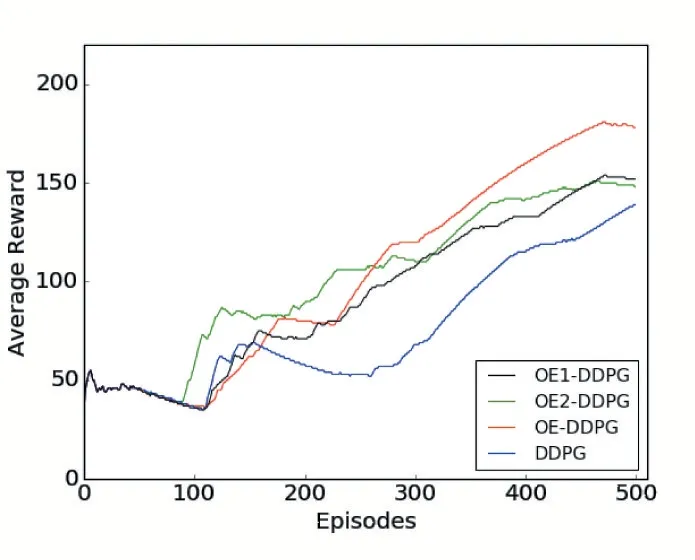
图6 中等环境算法比较
在复杂环境下的算法性能对比,如图7 所示。在仿真环境中,OE-DDPG 算法在100 代左右奖励开始逐渐提升,将最优动作与次优动作区分开,进行动作优化,直到训练结束效果都优于其他两个算法。而OE2-DDPG 算法的整体效果也由于OE1-DDPG 算法。无论是学习速率还是收敛速度都由于原始DDPG 算法,且算法OE-DDPG 的效果远超于原始DDPG 算法。
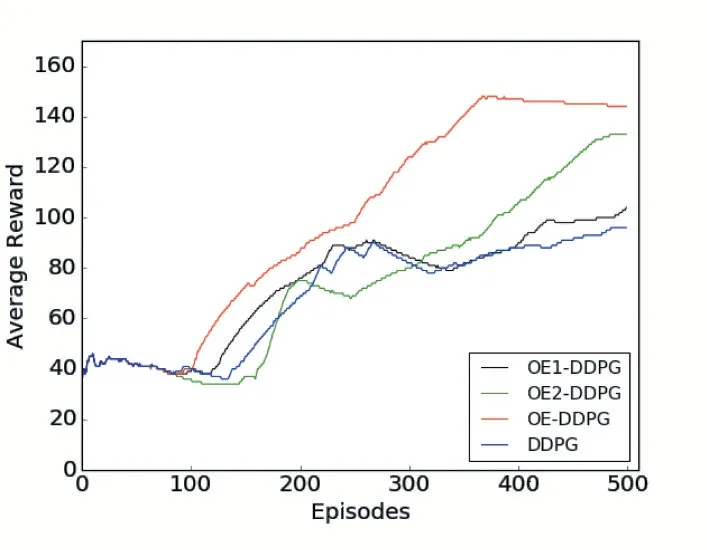
图7 复杂环境算法比较
通过无人驾驶汽车在简单、中等到复杂三个不同的仿真环境进行实验对比,本文提出的OE-DDPG 算法效果比原始DDPG 算法中使用的均方误差要好,所获得的平均奖励较高,也验证了算法的有效性和鲁棒性,同时可以看出OE-DDPG 算法能够快速适应无人驾驶环境。
4 结语
随着动作维度的增加,DDPG 算法在动作的连续控制和动作数量方面难以用离散的形式表示。另外,在动作维度较高的复杂环境下,DDPG 算法无法快速地确定最优动作和次优动作。针对这两方面的问题,本文提出了OE-DDPG 算法,并将其用于不同环境中的无人驾驶汽车的仿真中。结果显示OE-DDPG 算法能够使无人驾驶汽车快速和有效地避障,同时所获得的平均奖励也较高,并具有较好的鲁棒性。

