水声信道变步长自适应均衡算法

杨海斌

（湖南理工职业技术学院，湘潭411004）

0 引言

随着对海洋资源的进一步开发，水下通信在军事和民用方面发挥着越来越重要的作用。由于水下通道中电磁波衰减严重，声波成为唯一有效的通信方式。但与电磁波相比，声速极慢，容易引起严重的传播延迟。在传输信号时，由于水下通道的约束，声波会在海面和海底之间不断地反射。与其他通信信道相比，水声信道传输的信号具有复杂的多径传播特性，因而具有更强的符号间干扰。克服这种影响的最好方法之一是在接收机中使用自适应均衡方法[1]。由于自适应滤波器和自适应算法等因素的影响，选择计算复杂度低、跟踪信道变化能力强的自适应信道均衡算法显得尤为重要。在已知的水声信道自适应均衡算法中，最小均方（LMS）算法[2]和归一化最小均方（NLMS）算法[3]因其计算简单和实现简单而成为最流行的算法。在定步长LMS 算法中，步长因子不仅控制了算法的收敛速度，而且决定了算法的稳态误差。步长越大，收敛速度越快，稳态误差越大。当步长变小时，稳态误差变小，但收敛速度变慢。为解决固定步长算法收敛速度与稳态性能之间的矛盾，文献[4]提出了一种变步长算法，文献[5]根据实际水声信道时变、空变、多径的特点，提出了一种改进的变步长LMS 算法。

对于自适应均衡算法，除了需解决收敛速度和稳态失调之间的矛盾外，提高算法收敛速度也是国内外学者们研究的重点[6]。上述LMS 算法计算简单但收敛速度慢，递归最小二乘算法[7]由于其最快的收敛速度而成为最佳的自适应算法，但它的计算复杂度高，在自适应信号处理领域，仿射投影算法（APA）在收敛速度和计算复杂度之间取得了很好的平衡[8]。与LMS 算法相比，该算法的收敛速度大大提高，与递归最小二乘算法相比，计算复杂度大大降低。但仿射投影算法中，同样需要选择适当的步长，以达到收敛速度和稳态误差之间的折衷。因此，本文将干扰信号对均衡器稳态性能的负面作用考虑进滤波器系数更新过程中，通过重新设定系数更新约束条件，并利用先验误差向量的定义，得到了一种适用于仿射投影均衡算法的步长调节方法。新算法在未达到收敛状态时，采用较大的步长；在后期阶段使用较小的步长，从而有效解决了收敛速度与稳态误差之间的矛盾。实验结果表明，与传统的进化投影序列和变步长仿射投影算法相比，本文提出的算法具有更快的收敛速度和更低的失调率。

1 仿射投影算法

水声信道自适应均衡器通常采用图1 所示的结构。

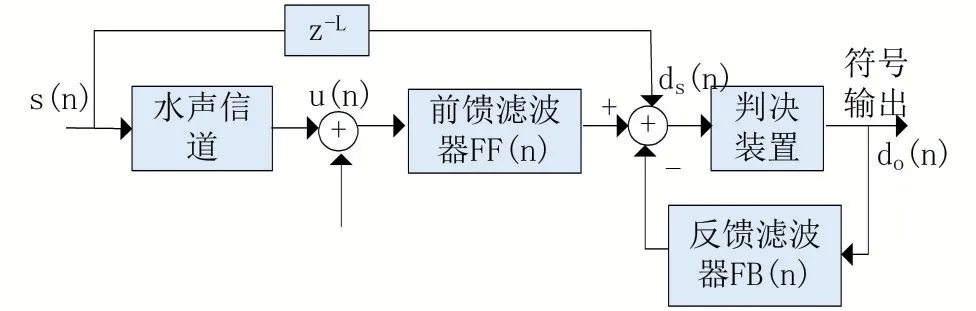
图1 水声信道自适应均衡器结构图

均衡器由FF（前馈）滤波器、FB（反馈）滤波器和判决装置组成输入信号s(n)经水声信道模型，并混合方差为的干扰噪声v(n)后，形成大小为NFF×1 的接收信号序列u(n)=[u(n)u(n-1)...u(n-LFF+1)]。

均衡器输出可表示为：

在APA 中，利用n时刻的前P个输入向量构成LFF×P维输入矩阵，加快了NLMS 算法的收敛速度，其系数迭代公式为[9]：

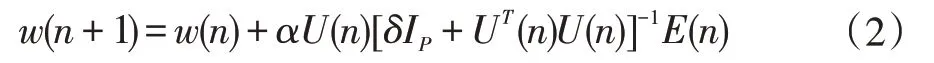
其中U(n)=[u(n)u(n-1)…u(n-P+1)]为LFF×P维输入矩阵，α是步长参数，δ是防止被零整除的小正数，IP为P×P维单位阵，E(n)为n时刻的前P个先验估计误差所构成的向量。

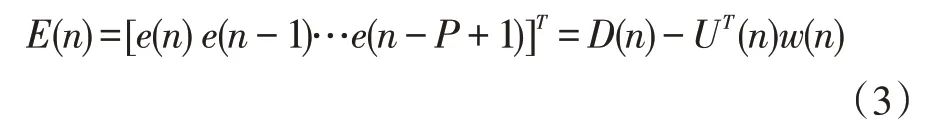
上式中D(n)=[d(n)d(n-1)...d(n-P+1)]为n时刻的前P个期望输出，于是有：

上式中w0(n) 为最优滤波器系数，V(n)=[v(n)v(n-1)...v(n-P+1)] 为噪声向量，并记ε(n)=[e(n)e(n-1)...e(n-P+1)]为n时刻的后验估计误差向量，于是有：

2 变步长仿射投影算法

针对水声信道h(n)引入的干扰噪声v(n)，本文提出改变传统仿射投影算法的约束条件，从(4)可以看出，传统仿射投影算法的约束条件迫使自适应滤波器补偿v(n)的影响。只要v(n)不为零，更新系数向量就不能等于未知系统的参数。为了使w(n)尽可能接近w0(n)，理想的约束条件应该是：

由于噪声是不可预测的，因此上述约束条件没有实际意义[10]。在本文中，我们使用二阶统计方法，使得式（6）两边的二阶统计量相等：

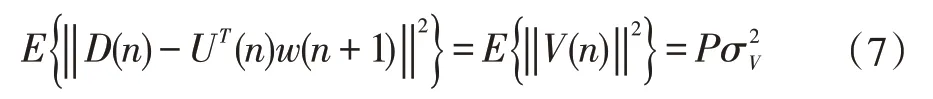
上式中表示噪声向量V(n)的方差，因变步长APA 算法步长不再为固定值，而是随着迭代的变化而变化，因此可用变步长参数向量α(n)=[α1(n)α2(n)…αP(n)]替换式（2）中的α，得到：

将上式代入式（6），并使用先验估计误差的定义，得到：

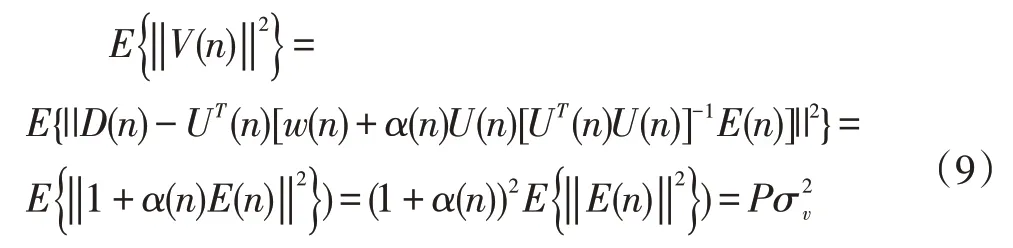
根据上式，可得到变步长仿射投影算法步长的迭代表达式为：

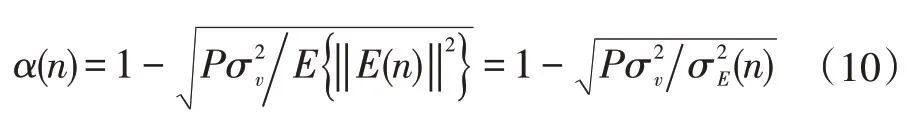
上式中(n)表示误差向量E(n)的方差，上式写成向量形式为：

3 仿真

为检验所提算法在信道均衡中的性能，采用文献[11]中的稀疏水声两径信道H(z)=1+0.4z-12，比较新算法（VSS-APA）与文献[8]（2016）所提定步长APA 算法、文献[3]（2017）所提变步长LMS 算法（VSS-LMS-1）及文献[4]（2019）所提改进的变步长LMS 算法（VSSLMS-2）的收敛性能。

仿真一比较了VSS-APA、APA、VSS-LMS-1 及VSS-LMS-2 四种算法的均方误差性能。该仿真中每帧传输包括512 次训练符号和1024 个数据符号，均衡器抽头个数为10，仿射投影阶数P=2 ，信号采用16QAM 调制方式，信噪比为10dB，APA 算法中步长α在分别取0.5 和0.8，仿真结果如图2 所示。从图中可看出，VSS-APA 与VSS-LMS-1 及VSS-LMS-2 相比，不仅收敛速度得到了提高，而且稳态性能也得到了改善。对于APA 算法，要获得与VSS-APA 相近的稳态失调，固定步长必须小于0.5，但此时收敛速度变得十分缓慢。APA（α=0.8）的初始收敛速度接近于VSSAPA 的收敛速度，与VSS-LMS-1 及VSS-LMS-2 的收敛速度相当，但其稳态失调较大。从图2 可看出，新算法能有效解决定步长APA 收敛速度与稳态失调之间的矛盾。

图2 算法均方误差收敛性能比较

仿真二比较了上述几种算法的误码率性能。在该仿真中，信噪比范围为-10 至14dB。信号采用QPSK调制方式，APA 算法中步长α取0.8，其他参数与仿真一中相同。仿真结果如图3 所示。由图3 可以看出，四种均衡算法在-10 至-5dB时误码率性能相仿，且随着信噪比增加而降低，但本文提出的误码率下降最快。当信噪比增加到5dB时，本文提出的VSS-APA算法误码率能达到2×10-3左右，APA 算法误码率接近5×10-2，VSS-LMS-1 算法和VSS-LMS-2 算法误码率约为8×10-2，充分证明了VSS-APA 算法良好的信道均衡性能。

图3 算法误码率性能比较

4 结语

本文考虑到传统仿射投影算法中约束条件迫使自适应滤波器补偿干扰信号的影响，通过建立一个新的约束条件，并利用先验误差向量的定义，得到了一种适用于仿射投影均衡算法的变步长调节方法。仿真结果表明，新算法的性能优于仿射投影算法和已有的变步长LMS 算法。