遗传算法优化神经网络的高校贫困生精准认定

肖琪

（常熟理工学院，常熟215500）

0 引言

习近平总书记明确提出，坚决打赢脱贫攻坚战，确保2020 年我国现行标准下农村贫困人口实现脱贫，脱贫县全部摘帽[1]。在脱贫攻坚战分层次分类的具体实践中，其中包括根据贫困地区的人力结构进行不同方式的教育扶贫[2]。教育扶贫领域，高等教育的精准扶贫工作至关重要[3]，一直是教育界甚至全社会广泛关注的问题。为了做好高等教育领域的精准扶贫[4]工作，很多高校都采取了建档立卡的方式实现精准资助[5]，但由于地方工作粗放，存在建档立卡贫困生识别不清的风险。

目前各高校主要根据教育部文件的相关要求对贫困生进行主观认定，这种认定方法存在很多主观因素，影响了评定结果的准确性。近年来，我国学者基于贫困生数据建立相关数学模型如决策树法[6]、模糊综合评价法[7]、层次分析法[8]、回归分析法[3]等，但以上方法各有利弊，如回归分析法针对线性关系的表达比较有效，而不能准确反映非线性关系。柴政等人[9]采用反向传播算法的前馈神经网络模型对高校贫困生等级进行评定，但容易陷入局部极小值。陆桂明等人[10]采用机器学习算法建立了XG-Boost 模型实现对高校贫困生等级的精确分类，但存在查准率较低的问题。

BP（Back Propagation）神经网络模型是一种非常重要而经典的人工神经网络，具有高度非线性、自学性和映射性等优点[12]，它不需要寻求非线性样本数据间的显性关系式和数学模型，便可以准确地逼近刻画训练样本数据规律的最佳函数，从而克服现有客观认定方法的许多局限性和困难。在实际应用中，BP 神经网络存在收敛速度慢以及局部极小值等问题。为此，本文采用自适应遗传算法（Adaptive Genetic Algorithm，AGA）优化BP 神经网络模型对高校贫困生等级进行精准认定。

1 认定指标体系的构建

1.1 认定指标的确定

本文利用常熟理工学院的学生样本收集贫困生认定数据。从资助管理系统中导出该校贫困生信息，从中随机抽取2015 名贫困生个体作为样本。根据任俊等人[10]采用多粒度粗糙集理论挖掘影响贫困生精准认定的关键性因素，从中筛选家庭人口数、父母亲职业、家庭收入、家庭住房情况等10 个认定指标作为输入变量，贫困生等级作为输出变量，具体如表1 所示。

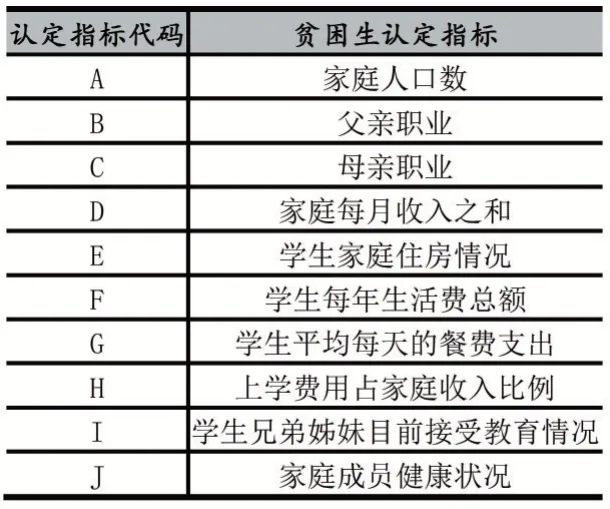
表1 贫困生认定指标体系

1.2 样本数据的量化

在对模型训练之前，需要对10 个认定指标进行量化处理。各指标的具体量化标准如表2 所示。如指标A 是指家庭人口数，赋值为1-4。当家庭人口数6 人及以上时，A 为1；当家庭人口数为5 人时，A 为2；当家庭人口数为4 人时，A 为3；当家庭人口数为3 人时，A为4。其他指标按照此方法进行量化。模型的输出变量是贫困等级，取值为1-3。当学生特别贫困时，贫困等级为1；当学生比较贫困时，贫困等级为2；当学生一般贫困时，贫困等级为3。

根据上述数据处理方法，得到认定指标量化数据如表3 所示。

在进行BP 神经网络预测之前，为避免原始数据过大造成网络麻痹，要对原始数据进行归一化处理。因此本文对表3 中的原始数据规范在[-1,1]之间，这样可以尽可能地平滑数据，从而消除预测结果的噪声，归一化的数据作为模型的训练样本。

表2 贫困生认定指标量化标准

表3 认定指标量化数据

2 自适应遗传算法优化模型

遗传算法（Genetic Algorithm，GA）是一种模拟自然界遗传机制和生物进化论而成的一种并行随机搜索最优化方法。遗传算法优化BP 神经网络简称（GA-BP）是用遗传算法来优化BP 神经网络的初始权值和阈值，使优化后的BP 神经网络能够更好地预测函数输出。交叉概率和变异概率是影响遗传算法性能的关键因素，因此，本文采用自适应遗传算法，通过自适应交叉概率和变异概率来提高遗传算法的性能。

GA-BP 模型是一种对网络的权重和阈值进行全局搜索的过程。具体的流程如图1 所示。

图1 GA-BP模型流程图

2.1 种群初始化

个体编码方法为实数编码，每个个体均为一个实数串，由输入层与隐含层连接权值、隐含层阈值、隐含层与输出层连接权值以及输出层阈值4 部分组成。个体包含了神经网络全部权值和阈值，在网络结构已知的情况下，就可以构成一个结构、权值、阈值确定的神经网络。

2.2 适应度函数

根据个体得到BP 神经网络的初始权值和阈值，用训练数据训练BP 神经网络后预测系统输出，把预测输出和期望输出之间的误差平方和的倒数作为个体适应度值f，计算公式如式（1）所示。

式中，n 为网络输出节点，yi为BP 神经网络第i 个节点的期望输出，oi为第i 个节点的预测输出，E 为误差平方和，f 为个体适应度值。

2.3 遗传操作

2.3.1 选择操作

遗传算法选择操作有轮盘赌法、锦标赛法等多种方法，本文采用轮盘赌法，即基于适应度比例的选择策略，每个个体i 的选择概率pi为式（3）所示。

式中，fi为个体i 的适应度值，pi为个体i 的选择概率。

2.3.2 交叉操作

由于个体采用实数编码，所以交叉操作方法采用实数交叉法，第k 个染色体ak和第l 个染色体al在j 位的交叉操作方法如式（4）所示。

式中，fmax为群体中最大的适应度值，favg为群体的平均适应度值，f’为要交叉的两个个体中较大的适应度值。k1,k2为常量系数，分别取（0，1）区间的值。

2.3.3 变异操作

选取第i 个个体的第j 个基因aij进行变异，变异操作方法如式（6-7）所示：

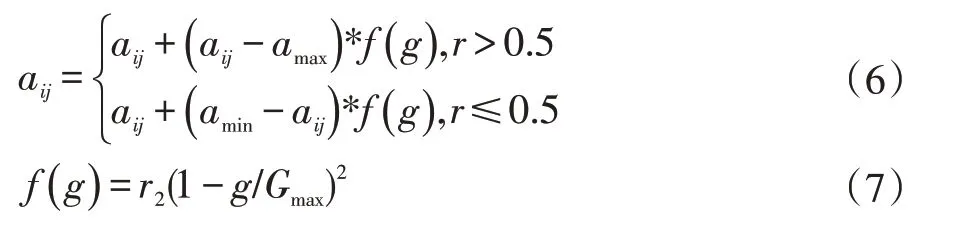
式中，amax为基因aij的上界；amin为基因aij的下界；r2为一个随机数；g 为当前迭代次数；Gmax为最大进化次数；r 为[0,1]间的随机数。

自适应变异概率根据式（8）进行计算。

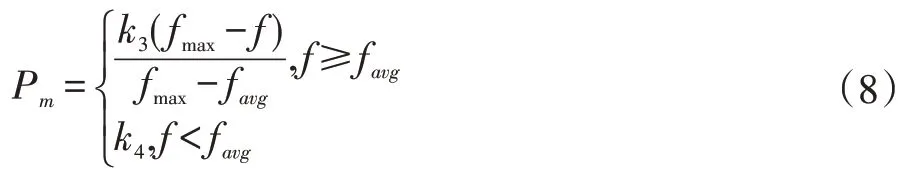
式中，fmax为群体中最大的适应度值，favg为群体的平均适应度值，f 为要交叉的两个个体中较大的适应度值。k3,k4为常量系数，分别取(0,1)区间的值。

3 模型的评价方法

本文对模型准确性的评价方法是根据预测等级与真实贫困等级之间的误差来判定的。误差的评估采用相对误差百分比、均方根误差和平均绝对误差作为评估指标，具体计算如式（9-11）所示。

式中，MAPE 为相对误差百分比，abs 为绝对值，A(i)为模型输出值，B(i)为实际值，k 为样本数量。

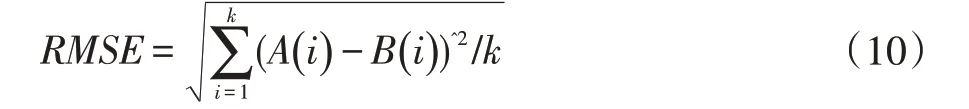
式中，RMSE 为均方根误差，k 为表示样本数量，A(i)为示模型输出值，B(i)为实际值。

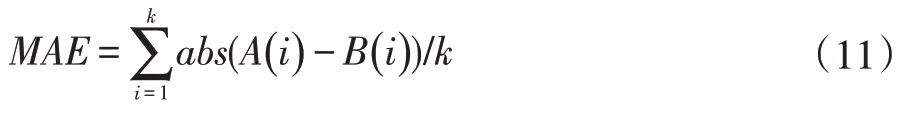
式中，MAE 为示平均绝对误差，abs 为绝对值，A(i)为模型输出值，B(i)为实际值，k 为样本数量。

4 模型的构建

4.1 隐含层节点数的确定

模型对高校贫困生等级进行预测，分为训练和验证两个部分。从表3 中选取1800 组数据作为训练样本，100 组数据作为测试样本，15 组数据作为验证样本。因此，训练样本的输入节点数为10，输出层节点数均为1，隐含层节点数根据公式（12）计算。

式中，N 为隐含层节点数，m 为输入节点数，n 为示输出节点数，a 为[1,10]之间的常数。根据式（12），本文隐含层节点取值范围为[4,13]。根据隐含层节点的取值范围，改变数值，

本文利用MATLAB R2016 自带的人工神经网络工具箱来完成模型的建立。根据隐含层节点数的取值范围对贫困生数据进行训练，不同隐含层节点数的BP 模型预测误差如表4 所示。从表4 可以看出，误差最小时对应的隐含层节点数为6。这主要是因为隐含层节点数过少时，不足以反映训练数据的客观规律，误差会出现波动；隐含层节点数数过多时，会增加网络学习时间，可能出现“过拟合现象”，也会导致误差较大。因此，隐含层节点数的选取要适中。

表4 不同隐含层节点数BP 模型的预测误差

4.2 输入层和输出层的传递函数确定

输入层和输出层的传递函数选取宗旨是使预测准确。在网络结构和权值、阈值相同的情况下，BP 模型预测误差与隐含层、输出层的传递函数之间的关系如表5 所示。

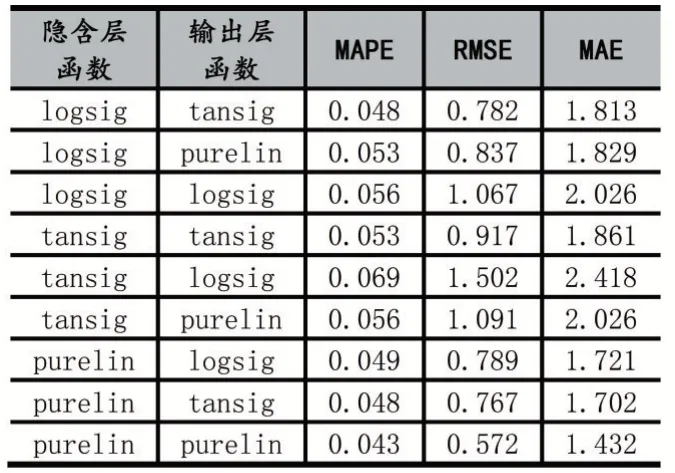
表5 不同传递函数对应的预测误差

从表5 可以看出，隐含层和输出层的传递函数选择对BP 模型预测精度有较大影响。其中误差最小的隐含层和输出层的传递函数分别为purelin、purelin。

4.3 训练参数的确定

根据上述模型参数的确定，相关训练参数的设置如表6 所示。

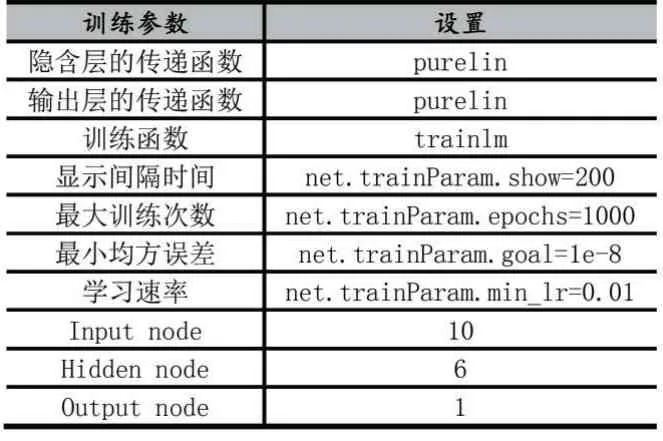
表6 训练参数的设置

根据上述训练参数，训练BP 神经网络。高校贫困生的贫困等级预测值与实际值对比结果如图2 所示。从图2 可以看出，BP 模型对贫困生等级的预测结果与实际贫困等级之间偏差比较大。实际值和预测值之间的接近程度一般采用相关系数来表征。对BP 模型的预测结果进行相关性分析，结果如图3 所示。从图3可以看出，BP 模型对贫困生的贫困等级预测的相关系数为0.23。

5 结果与讨论

采用GA-BP 模型、AGA-BP 模型分别对网络进行训练和测试。GA-BP 模型的测试结果如图4 所示。从图4 可以看出，GA-BP 模型对贫困生等级的预测值与实际值的接近程度比BP 模型有所改善。这主要是因为GA-BP 模型克服了局部最小值的缺陷。对贫困生等级的相关度分析如图5 所示。从图5 可以看出，GA-BP 模型对贫困生等级预测的相关系数为0.80。与BP 模型的相关系数对比，GA-BP 模型在预测相关性上有所改善。

AGA-BP 模型的测试结果如图6 所示。从图6 可以看出，AGA-BP 模型对贫困生等级的预测值与实际值比较一致。这主要是因为AGA-BP 模型相比GABP 模型来说，通过不断调整交叉概率和变异概率，更能够平衡局部搜索和全局搜索能力，有效避免了GABP 模型出现早熟收敛问题，从而找到内部最优解。AGA-BP 模型贫困生等级的相关度分析如图7 所示。从图7 可以看出，AGA-BP 对贫困生等级预测的相关系数为0.96。与GA-BP 的相关系数对比，优化模型在预测相关性上有了很大改善。

为了验证遗传算法优化模型的优越性，利用15 组验证样本数据对三个模型的预测精度进行验证，结果如表7 所示。从表7 可以看出，AGA-BP 模型的预测误差最小，即预测精度最高。因此，AGA-BP 模型的预测效果比BP 模型、GA-BP 模型的预测效果更好。

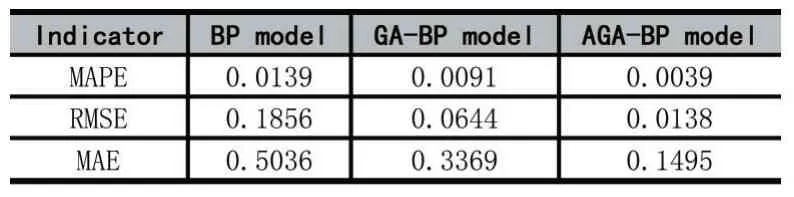
表7 各模型的预测误差对比

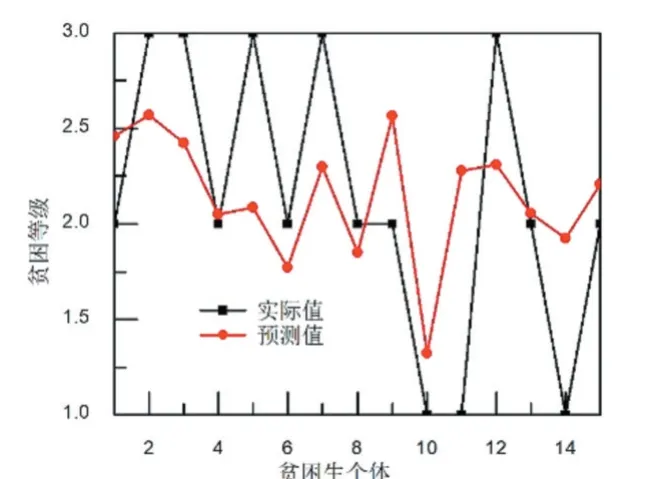
图2 BP模型的预测结果

图3 BP模型的相关性分析

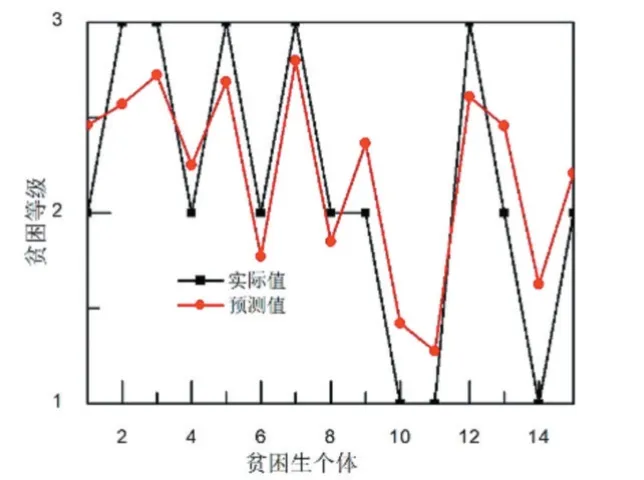
图4 GA-BP 模型的预测结果

图5 GA-BP 模型的相关性分析

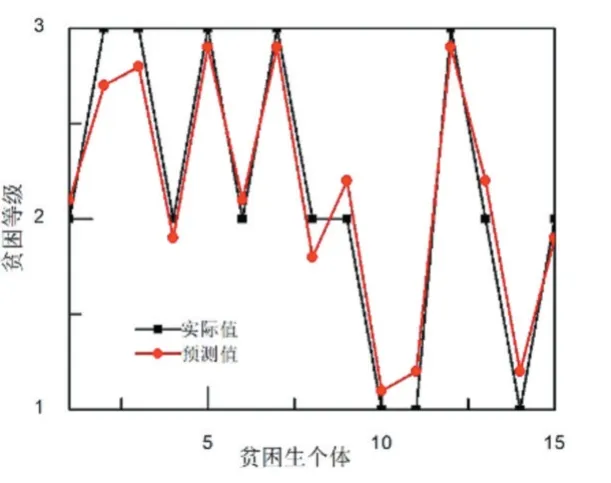
图6 AGA-BP 模型的预测结果

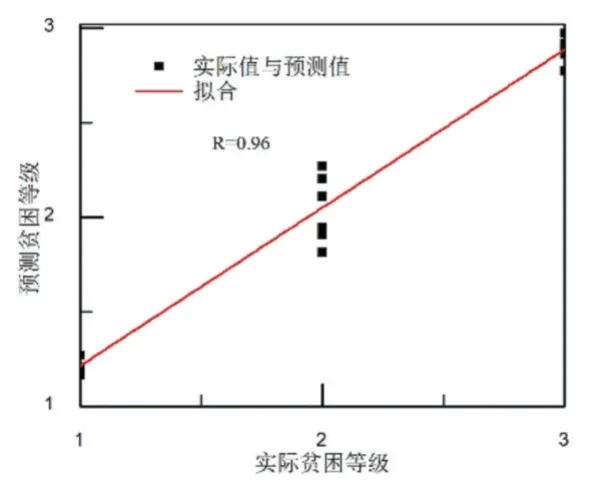
图7 AGA-BP 模型的相关性分析

6 结语

自适应遗传算法优化的BP 神经网络模型能有效表明具有非线性关系的输入量与输出量之间的关联性。由于高校贫困生等级与其主要认定指标间存在着复杂的非线性关系，筛选家庭成员数、父亲职业、母亲职业等10 个认定指标作为神经网络模型的输入参数，对高校贫困生等级进行预测，对比了BP 模型、GA-BP模型、AGA-BP 模型的相关系数、预测精度。结果表明，采用自适应遗传算法优化的BP 神经网络模型预测贫困生等级更接近真实情况，充分说明自适应遗传算法优化神经网络对高校贫困生精准认定的有效性。