对发展学生数学思考的思考

王燕

摘要：数学学科有其独特的学科育人价值。数学课堂不能仅仅停留在表面的“有意思”，而是应该追求“有意义”的学习建构，促使学生形成“以思为乐” 的积极学习心向，发展数学思考。教师要发挥组织引导作用，通过深度开发教材，变化拓展，为学生提供思考的载体;灵活处理课堂生成，为学生营造思考的场域。

关键词：小学数学;数学思考;教材开发;课堂生成

人之所以伟大，在于其能够独立思考和善于思考。数学学科有着独特的学科育人价值。数学课堂不能仅仅停留在表面的“有意思”，而是应该追求“有意义”的学习建构，促使学生形成“以思为乐” 的积极学习心向，发展数学思考。立足自身的教学实践经验，笔者在此提出几点思考。

一、教材内容再开发，提供思考的载体

教材是小学生数学学习的重要载体。因此，教师应尽可能地挖掘教材，在例题延伸中，激活学生的数学思考;在变式练习中，发展学生的发散思考能力。

（一）例题延伸

例如，苏教版小学数学五年级下册教材在讲解了分数乘整数的意义和计算法则以后，介绍了“可以先约分，再计算”的方法，但教材中的例子612不能让学生明显地感觉到先约分的必要性。为此，在学生掌握了分数乘整数的计算方法并进行了一定练习以后，笔者出示算式 29999×7777，让学生比一比，看谁算得又对又快。学生眼前一亮，興致勃勃地开始计算，但很快便觉得2与7777相乘计算比较麻烦。这时，笔者引导学生观察：“题中的数字有什么特点，怎样算比较简便呢？”许多学生通过思考，恍然大悟，自觉地运用了先将7777与9999约分，然后再将7和2相乘的方法。

在例题教学后进行延伸，为学生提供自主探究的场域，促其自然得出“分数和整数相乘，先约分再乘比较简便”这一结论。这显然比直接告知学生更能激活他们的思考。

（二）变式练习

变式练习，是指改变问题的非本质特征，从而凸显问题本质特征的练习。在高年段小学数学教学中，尤其要强化变式练习。这就需要教师真正把“用教材教”落到实处，通过改编题目的方式发散学生的思考，并最终归拢到问题的本质上。这样，不仅能培养学生的发散思考能力，更能锻炼学生分析问题和解决问题的能力。

例如，在教学“立体图形的表面积”时，笔者展开了如下教学：

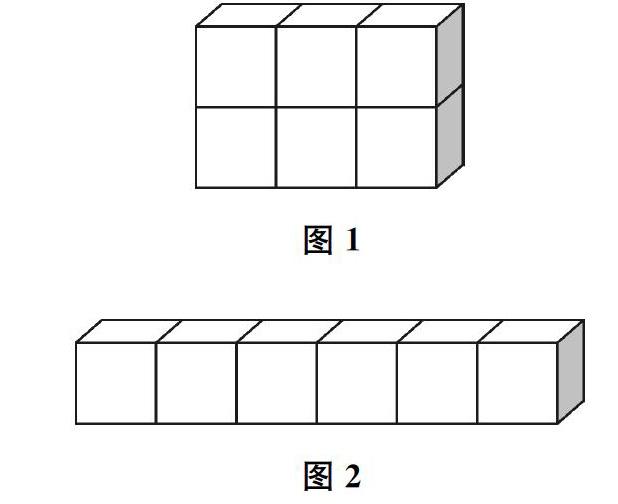
师（出示图1、图2）用6个体积是1立方厘米的正方体可以拼成不同的长方体，哪个长方体的表面积大？大多少？

（学生交流讨论解题思路和方法。）

师6个正方体还可以拼成怎样的立体图形？拼成的图形表面积是多少？体积是多少？

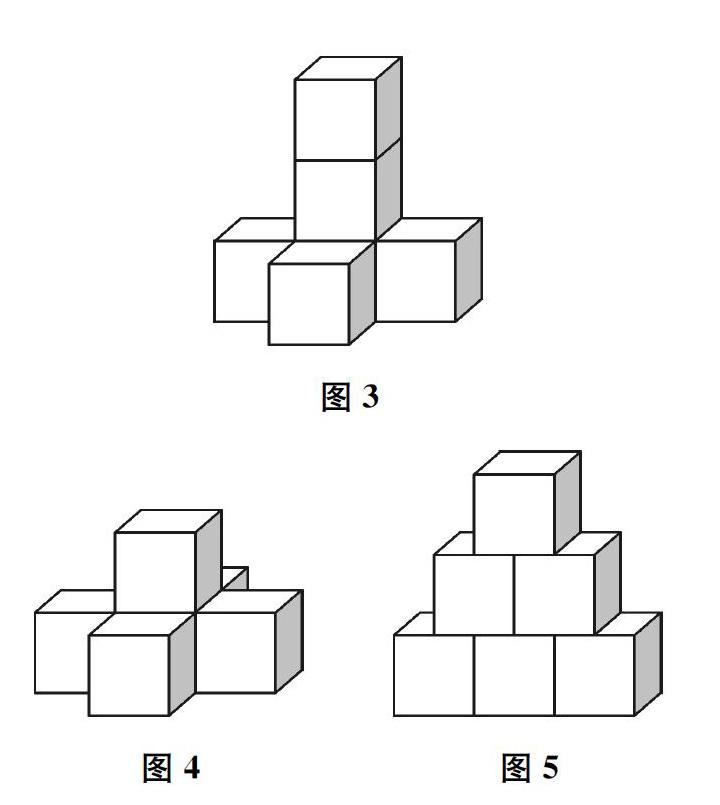
生（展示拼法，如图3）可以拼成这样，前后两面合起来是10平方厘米，左右两面合起来是8平方厘米，上下两面合起来是8平方厘米，总共是26平方厘米。因为是6个小正方体，所以体积是6立方厘米。

师还可以怎样拼呢？

（学生展示交流拼法，部分学生拼法如图4、图5所示。）

师这么多拼法，在算表面积和体积时，有什么好办法吗？

生算表面积时，可以算出前面和后面、上面和下面、左面和右面分别是几平方厘米，然后加起来;算体积时，有多少个小正方体，面积就是几立方厘米。

本节课，笔者通过“还可以拼成怎样的立体图形？”这一问题，引导学生发散思考，进而让学生归拢方法的实质：拼法是非本质特征，无论怎么拼，在求类似立体图形的表面积时，本质方法是一致的，都是先算一个面的面积，再数数一共有几个这样的面，优化得到从前面、左面、上面看分别有几个面的方法。这样发散思考的过程中，学生学习的积极性、主体性充分发挥，在深刻理解知识的同时提升了空间想象能力。

二、灵活处理课堂生成，营造思考的场域

（一）在比较中降低思考的坡度

在解决问题时，有些问题的条件是内隐的，需要学生仔细分析与挖掘。部分学生会用自己的方式将问题中隐含的条件显现，让内隐的想法外显，使得问题变得直观、形象。这需要教师有一双善于发现的眼睛，抓住学生的“灵光”，引导全班交流，在比较中降低思考的坡度。

有这样一道题：暑假期间，小林每6天游泳一次，小军每8天游泳一次，7月31日两人在游泳池相遇，那么8月几日他们又会再次相遇？有的学生通过在日历上按要求圈一圈找出了答案，有的学生通过找最小公倍数的方法解决了问题，有的学生两种方法都用了。笔者在巡视时发现了一个学生的“特殊”解法（如图6），据此展开了教学：

师说说看，你为什么列式0+24=24？

生和最小公倍数有关。在此相遇，说明这个时间既是小林游泳的时间，也是小军游泳的时间，也就是他们俩游泳时间的倍数，即找6和8的最小公倍数。

师为什么要列0+24=24这样的算式？“0”表示什么？从哪里来的？

生（边回答边在日历上比画）他们两人第一次相遇是在7月31日，我们可以理解成8月0日，再过24天所以要加上24，得到下一次相遇的时间是8月24日。

师这道算式中两个“24”的含义一样吗？

生两个“24”是不一样的，加数“24”是再过24天，而和“24”是8月24日，是一个日期。

师没错，通过“24”与“24”的比较，我们就把一段时间与某一天区分开了，对0+24=24这个算式也理解得更深刻了。如果两人第一次相遇是在8月7日，那么他们再一次相遇是在几月几日？

生7+24=31，8月31日。

师通过比较我们发现，在这种“相遇”问题中，只要用第一次相遇的时间，加上经过的天数，也就是两个数的最小公倍数，就等于下次相遇的日期。

生老师，还可以再举一些例子进行验证，如第一次相遇的日期是8月10日……

可以看出，提出“特殊”解法的学生对这道题的理解很深，能够利用画图、举例的策略，把一些隐含的条件显性化，使较难的问题变得形象化、简单化。而教师及时抓住学生的生成，带领全班学生感受内隐条件外显的过程，进而，引导学生通过比较，主动展开思考，发现一类题的解题规律，感受数学思考的乐趣。

（二）在碰撞中擦出智慧的火花

犯错是每个学生的权利，也是每个学生成长的必然经历。经历错误、纠正错误、反思错误，恰恰是学生成长过程中的宝贵财富。在课堂上，错误也是学生深入思考的重要资源。借助对错误的辨别与反思，学生在对比中掌握知识，在碰撞中擦出智慧的火花。

有这样一道思考题：“等腰直角三角形的一条边是8厘米，它的面积最大是多少平方厘米？最小是多少平方厘米？”问题一出，有学生立刻给出了自己的答案（如图7、下页图8）：“等腰直角三角形的一条边是8厘米，它是直角边时三角形的底和高都是8厘米，面积是最大的;而当8厘米为等腰直角三角形的斜边时，面积是最小的。”另一位学生脱口而出：“那两条边是5和5。”其他学生连声附和。对于学生的错误，笔者没有急于否定，而是让学生静下心来思考：“别急，可以先画一画、算一算。”

五分钟后，小张同学展示了如图9的做法并汇报了他的想法：“我同意面积最大是32平方厘米的解法，但我認为，面积最小不是12.5平方厘米，应该是16平方厘米。”

“为什么呢？”其他学生纷纷质疑。小张同学答道：“因为这是一个等腰三角形，要使面积最小，底边一定是8厘米，作出底边上的高一定是4厘米，因为两个底角是45度，那被高分成的两个小三角形也必然是等腰三角形，最后算出整个三角形的面积就是16平方厘米。”笔者适时引导：“我们来分析一下，为什么12.5平方厘米不对呢？”学生回答：“因为无法证明那条直角边到底是不是5。”“是啊，无法证明的结果就不能当作条件来使用，这个时候就需要换一个思路了。”笔者这样小结。就在这样的碰撞中，学生擦出了智慧的火花，生成了另一种解法：如图10，最小的等腰直角三角形的面积=8×8÷4=16（平方厘米）。

让学生“以思为乐”，不仅是通过设计学生感兴趣的情境来让他们“乐学”，也不仅是让他们停留在浅层的、表面的、流于形式的思考，更重要的是，要促使他们追求对数学深层的、本质的、实质的思考，真正感受到数学的魅力，体验到“真思”的快乐。这要求教师要发挥组织引导作用，通过深度开发教材，变化拓展，为学生提供思考的载体;灵活处理课堂生成，为学生营造思考的场域。与此同时，在教学中，教师要放慢速度，给予学生思考与整理的时间和空间，让学生尝试自主建构数学知识，获得“数学其实很简单、一通百通”的体会，做“快乐的数学思想者”。