应用型高校线性代数课程改革与探索

李玉霞，杨立星

(泰山科技学院，山东 泰安 271038)

1 应用举例

1.1 线性方程组的应用

例1：投入-产出问题。

某个经济体由农业、矿业、制造业三个部门构成。已知农业部门将5%的产出销售给矿业部门，30%的产出销售给制造业部门，农业部门保留余下的产出。矿业部门将20%的产出销售给农业部门，70%的产出销售给制造业部门，矿业部门保留余下的产出。制造业部门将20%的产出销售给农业部门，30%的产出销售给矿业部门，制造业部门保留余下的产出。分析每个部门总产出，使得每个部门投入产出达到平衡。

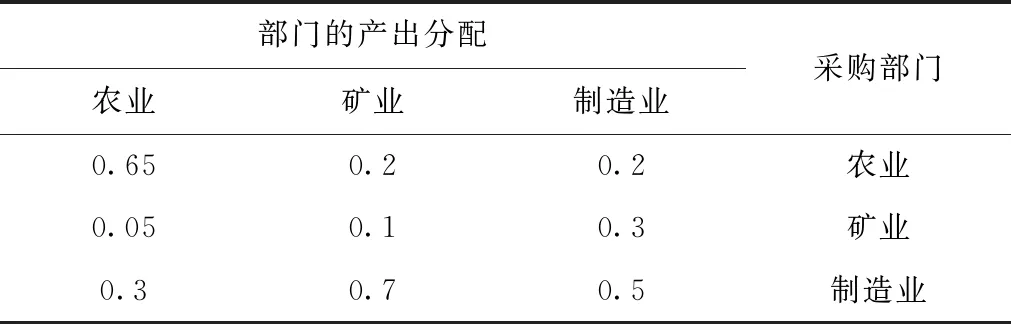
部门的产出分配农业矿业制造业采购部门0.650.20.2农业0.050.10.3矿业0.30.70.5制造业

现假设农业、矿业、制造业三个部门的产出分别为：x1,x2,x3，上述表格中，每一列表示相应部门产出的去向，例如第一列表明农业部门的0.65x1产出自留，0.05x1的产出流向矿业部门，0.3x1的产出流向制造业。表格中，每一行表示相应部门需要采购不同部门投入比例，例如第一行表明农业部门需要农业部门投入0.65x1，矿业部门投入0.2x2，制造业部门投入0.2x3。要使得农业部门投入产出平衡，有

x1=0.65x1+0.2x2+0.2x3

(1)

同理，要使得矿业、制造业部门投入产出平衡，可得：

x2=0.05x1+0.1x2+0.3x3

(2)

x3=0.3x1+0.7x2+0.5x3

(3)

联立(1)(2)(3)可构成线性方程组

通过移项，可得齐次线性方程组

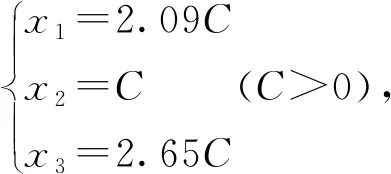
1.2 矩阵的应用

例2：某企业一年生产甲、乙、丙三种产品，每种产品的生产均需用A1,A2两种原料，完成一年生产任务需要A1,A2的数量及原料单位价格、单位质量及单位体积如下表所示。

原料数量/单位甲乙丙单位价格/万元单位质量/吨单位体积/m3A14 0002 0001 5000.60.030.5A23 5001 8001 2000.50.040.6

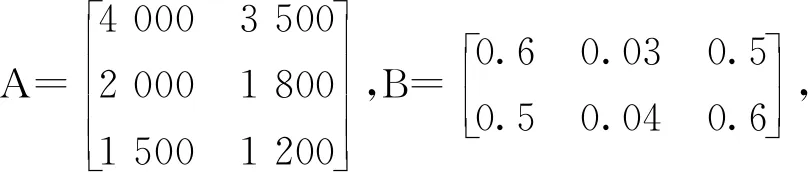
1.3 特征值与特征向量

首先建立(xn,yn)T的递推模型，根据给出的条件可知

化为矩阵形式可得

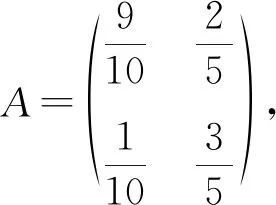
随着时间的推移(n→+∞)，

2 结语

将应用实例引入课堂，有助于学生将数学基础知识与专业知识进行融合，提高主观能动性。