基于多阶导数拉曼光谱组合技术的矿物油模式分类

卫辰洁，王继芬*，张 波，董 泽，管建皓

(1.中国人民公安大学 侦查学院，北京 102600；2.伊犁州伊宁市公安局，新疆 伊宁 835000;3.中国 人民公安大学 治安学院，北京 102600；4.中国人民公安大学 犯罪学学院，北京 102600)

矿物油的检验与鉴定是法庭科学领域的重要工作之一。其中，重质矿物油是一种由石油分馏且沸点较高的矿物油，在日常生活中被作为工业原料广泛应用于机械润滑、汽车修理、交通运输等领域。它的成分复杂、种类繁多，不同品牌和类别的重质矿物油在组成成分和加工工艺上存在很多差异[1-2]。在纵火、焚尸、凶杀、交通肇事等案件现场中，经常会提取到相关的物证。通过对现场提取的重质矿物油物证和犯罪嫌疑人处提取的重质矿物油物证进行比对检验，可为确定犯罪嫌疑人提供线索和依据。

光谱组合技术在分析测试领域具有良好的应用前景。通过光谱组合技术将多种光谱数据矩阵进行结合，可以避免单一光谱和数据矩阵信息不够丰富的缺点，综合多种数据所包含的信息进行分析，从而获得更全面有效的光谱和数据信息。利用不同数据的冗余特征与互补特征重新进行信息的组合，克服了单独一种光谱或一种数据存在的弊端，实现了光谱特征或对应数据特征的优势互补，可达到优化实验数据的目的。目前，针对光谱数据组合的研究较少，在法庭科学领域更是少之又少。胡翼然等[3]利用光谱数据组合的策略对绒柄牛肝菌的产地进行探究，通过结合随机森林算法对多种特征值进行提取，比较其对算法分类准确率的影响，实现了对绒柄牛肝菌产地的快速、准确和廉价的鉴别。傅里叶变换拉曼光谱分析法结合近红外激光拉曼技术和傅里叶变换技术,具有不损坏样品、扫描速度快、灵敏度高、操作简单、样品用量少等特点，在化工材料[4-5]、食品安全[6]、环境污染[7-8]、药品原辅料[9]等检测领域得到应用。在法庭科学领域，傅里叶变换拉曼光谱分析技术应用相对较少，主要用于几种常见物证的检验[10-11]。

基于快速、无损、准确检验物证的目的，本文利用傅里叶变换拉曼光谱技术采集了重质矿物油样本的原始光谱、一阶导数谱和二阶导数谱数据，通过构建分类模型的方法对单独的光谱数据和组合后的光谱数据的分类效果进行比较，以期达到对重质矿物油样本的准确鉴别和区分，为光谱组合技术在法庭科学及其他分析测试领域的应用提供一定的借鉴。

表1 80个样本的基本信息Table 1 The details of 80 samples

1 实验部分

1.1 实验样本

在山东、北京、河南等地区的机械加工厂和车辆维修厂收集到80种不同型号、不同厂家的重质矿物油样本，主要包括汽机油、柴机油、润滑脂、齿轮油、液压油5种类别和多种品牌(如表1所示)。

1.2 光谱采集

样本预处理：对收集到的80种不同重质矿物油样本进行编号。

光谱参数：采用傅里叶变换红外-拉曼光谱仪进行光谱采集(具体信息如表2所示)。扫描次数为64次，光谱分辨率为8.000 cm-1，测量范围为3 600～400 cm-1。以汽机油为例，图1A展示了一种典型汽机油的光谱图。

多阶求导：利用光谱数据处理软件OMNIC 8.2对采集的光谱数据进行多阶求导。由于光谱数据受噪声影响较小，采用不过滤的方式，选择最简单的“First difference derivative”进行求导。分别对原始光谱数据进行一阶导数和二阶导数处理，保留光谱原始数据、一阶导数数据和二阶导数数据矩阵。图1B和图1C分别展示了该种典型汽机油的一阶导数与二阶导数的光谱图。

实验环境：具备暗室条件，不受阳光直射；无强振动源，无电磁干扰。

表2 仪器的基本信息Table 2 The details of instrument

图1 典型汽机油的拉曼光谱图(A)、一阶导数拉曼光谱图(B)及二阶导数拉曼光谱图(C)
Fig.1 Raman spectra(A),Raman spectra of the first derivative(B) and Raman spectra of the second derivative(C) of typical turbine oil

1.3 建模原理

径向基函数神经网络模型(Radial basis function neural network，RBF)[12]属于神经网络模型中的一种。作为一种局部逼近网络，它具有训练简洁、训练速度快、可以很快逼近任意非线性函数的特点。RBF包含3层结构，即输入层、隐藏层和输出层。输入层仅负责输入数据；隐藏层作用函数为径向基函数，对输入数据每层的网络可能只有一个神经元被激活，所以属于局部逼近；输出层的每个神经元属于线性求和单元，输出的是隐藏层各单元输出的加权和。RBF的基本思想是通过映射将低维度线性不可分的原始数据投至高维空间，从而使数据线性可分。

K最近邻算法(K nearest neighbor algorithm，KNN)作为一种常见分类和回归模型，具有理论成熟、准确度高、可用于非线性分类等特点。其具体过程为，通过计算每个样本点的距离，对所有距离进行排序，选取前K个距离最小的样本，根据所选取的样本标签进行投票，从而确定样本的归类。其中，K值的选择尤为重要，K值较大时能够减小噪声影响，但会导致类别界线变模糊；K值较小时“学习”的近似误差会减小，但容易导致过度拟合。实际应用中，一般选用交叉验证等启发式技术来选取最优的K值。

实验采用Statistical Product and Service Solutions-20数据处理软件对保留的多阶导数光谱数据构建分类模型。

2 结果与讨论

2.1 径向基函数神经网络模型(RBF)

为了消除数据之间的量纲关系，方便函数模型的比较，首先对原始光谱、一阶导数谱和二阶导数谱数据进行标准化处理，并将标准化值作为分类的变量。实验以重质矿物油样本的5种类别为依据，即汽机油、柴机油、润滑脂、齿轮油、液压油。将80个重质矿物油样本分为训练样本和测试样本，比例分别为70%和30%，即56个训练样本和24个测试样本。运用RBF模型分别对单独的原始光谱、一阶导数谱、二阶导数谱数据以及组合的原始光谱+一阶导数谱、原始光谱+二阶导数谱、一阶导数谱+二阶导数谱数据进行分析，得到样本的分类结果(见表3)。

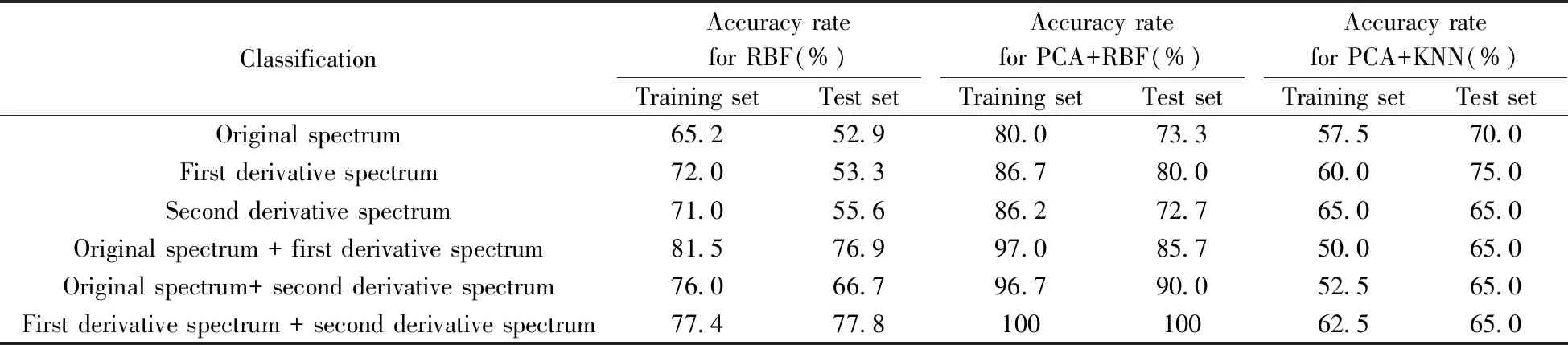
表3 分类结果摘要Table 3 Summary of classification results

图2 原始变量的重要性Fig.2 Importance of original variable

由表3可以看出，将原始光谱与导数光谱组合之后，模型训练集和测试集的分类准确率均有明显提升,但总体分类准确率均较低，实验结果不太理想。以原始光谱数据为例，图2展示了对原始光谱构建的RBF模型中各变量的正态化重要性程度。一般认为，正态化重要性大于60%为比较重要，在40%～60%之间其次，小于40%则重要性程度不明显。从图中可以看出，原始光谱数据中存在一半以上的变量对构建分类模型重要性程度较低。分析认为，大量的原有光谱数据之间存在较强的线性相关性且冗余信息较多，从而影响了模型分类的准确率。

主成分分析(PCA)作为一种数据降维的方法，可以有效地处理变量之间的多重共线性问题。尤其是面对大量数据时，PCA可以提取原始数据的主要成分，用尽可能少的新变量来概括原有变量的特征[13-15]。基于此，实验通过Statistical Product and Service Solutions-20数据处理软件采用PCA对原始光谱数据和导数光谱数据进行降维，提取数据的主要特征后再次进行分类。

表4为原始光谱数据的PCA结果。从表中可以看出，每个新变量对原始数据的解释方差不同。在实际应用中，需选取解释原始数据方差比例高的变量作为主成分。通常有两个判断标准，特征根大于1且满足累计方差贡献率大于85%[16]。因此，选取前10个成分作为主成分，累计方差贡献率为98.647%，即前10个成分解释了98.647%的总方差，可以涵盖原始数据98.647%的信息。同样条件下，对一阶导数谱、二阶导数谱数据以及组合的原始光谱+一阶导数谱、原始光谱+二阶导数谱、一阶导数谱+二阶导数谱数据提取主成分，分别提取了前39个主成分，累计方差贡献率均达到100%，主成分提取结果理想。

表4 主成分分析结果摘要Table 4 Summary of principal component analysis results

分别对提取主成分后的原始光谱、一阶导数谱、二阶导数谱数据以及组合的原始光谱+一阶导数谱、原始光谱+二阶导数谱、一阶导数谱+二阶导数谱数据构建RBF模型，得到了分类结果(见表3)。

图3 主成分变量的重要性Fig.3 Importance of principal component variables

由表3可知，通过PCA方法降维后，RBF模型的准确率明显提高。图3展示了对原始光谱数据进行PCA方法降维后提取的主成分在RBF分类模型中的正态化重要性。从图中可以看出，在此次模型预测中，PCA提取的10个主成分对模型的重要性均在40%以上，即10个主成分均对模型的分类比较重要。与原有变量相比(见图2)，主成分在模型分类中的重要性更为明显。分析认为，PCA降维后的数据消除了原有数据的线性相关性和冗余信息，使得提取的主成分不仅可以代表原有数据，而且更适用于模型分类。在对组合的原始光谱+一阶导数谱、原始光谱+二阶导数谱、一阶导数谱+二阶导数谱数据进行分类中，训练集的分类准确率分别达到97.0%、96.7%、100%，测试集的分类准确率分别达到85.7%、90.0%、100%，远高于单独的原始光谱、一阶导数谱和二阶导数谱数据的分类效果，且分类结果理想。其中，基于一阶导数谱+二阶导数谱数据的PCA+RBF模型的分类准确率最高，对重质矿物油样本的5种类别均实现准确分类，分类准确率达到100%。分析认为，原始光谱与导数光谱组合后，数据信息结合了两者各自的优势，尽可能多地反映了重质矿物油样本不同类别之间的差异，达到了优势互补的目的。

图4 K值选择的错误率Fig.4 The error rate of K value selection

2.2 K近邻算法(KNN)模型

在KNN分类中，运用训练样本即为测试样本的方法进行交互验证[17]，并采用交叉验证方法选择最优的K值。以原始光谱PCA提取主成分后的数据为例，图4展示了交叉验证中K值选择的错误率。从图中可以看出，K值在1～6时，选择错误率在0.4以下浮动，且在K值为5时错误率最低，为0.275 8；当K值大于6时，错误率明显提升，均在0.4以上。因此，在该数据下构建KNN分类模型时，选择K=5作为最优K值。同样条件下，交叉验证分别选择K为3、1、22、5、3作为一阶导数谱、二阶导数谱数据以及组合的原始光谱+一阶导数谱、原始光谱+二阶导数谱、一阶导数谱+二阶导数谱PCA提取主成分后数据的最优K值；并分别选择K为1、4、2、2、4、3作为原始光谱、一阶导数谱、二阶导数谱数据以及组合的原始光谱+一阶导数谱、原始光谱+二阶导数谱、一阶导数谱+二阶导数谱的原有数据的最优K值。

基于交叉验证选取的K值，对原始光谱、一阶导数谱、二阶导数谱数据以及组合的原始光谱+一阶导数谱、原始光谱+二阶导数谱、一阶导数谱+二阶导数谱的原有数据构建KNN分类模型，并对PCA降维后的数据进行KNN分类(见表3)。

从表3可以看出，KNN模型对重质矿物油样本的分类结果并不理想，无论是PCA降维之后，还是原始光谱与导数光谱组合之后，分类准确率均较低。分析认为，KNN分类模型受到样本不均匀的影响。由于80个实验样本包括了40个汽机油类型、22个柴机油类型、8个润滑脂类型、6个齿轮油类型和4个液压油类型，其最大样本数和最小样本数的相差较大，使得KNN模型分类时更多的将预测样本侧重于样本数多的汽机油类型，从而导致不能准确分类，影响了总体分类的准确率。

2.3 不同品牌的分类模型

通过对组合的光谱数据建立不同的分类模型，发现基于一阶导数谱+二阶导数谱数据的PCA+RBF模型分类效果最好。因此，实验采用最优模型对同种类别下不同品牌的重质矿物油样本进行分类(见表5)。

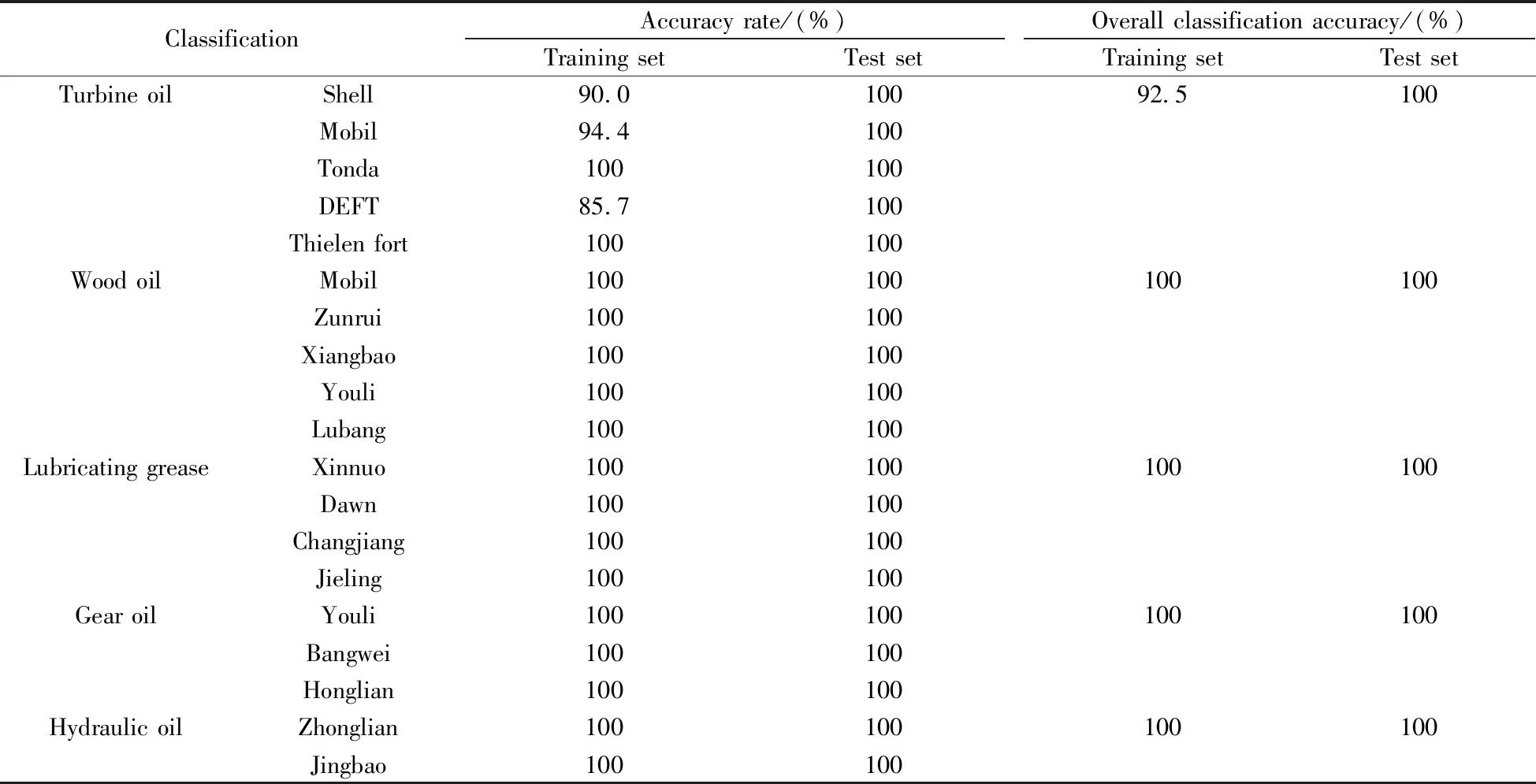
表5 PCA+RBF分类结果摘要Table 5 Summary of PCA+RBF classification results

由表5可以看出，基于一阶导数谱+二阶导数谱数据的PCA+RBF模型对于汽机油类别下的品牌，测试集样本均实现了准确分类，分类准确率为100%；对于训练集样本，富田和帝伦堡两种品牌实现了准确区分，分类准确率均为100%，而壳牌、美孚和德弗特3种品牌的训练集样本存在误判，分类准确率分别为90.0%、94.4%和85.7%，从而使得训练集样本的总体分类准确率为92.5%，即40个汽机油样本中存在3个样本的品牌类型被错误判断。分析认为，在模型的训练中受到样本数较少的影响，发生了一定概率的误判。对于柴机油、润滑脂、齿轮油、液压油4种类别下的不同品牌，该模型均实现了准确分类，训练集和测试集样本的分类准确率均为100%，实验结果理想。这表明，基于一阶导数谱+二阶导数谱数据的PCA+RBF模型可实现对不同类别和不同品牌重质矿物油样本的准确区分，且满足快速、准确、无损的要求。

3 结 论

本文利用傅里叶变换拉曼光谱技术结合化学计量学构建分类模型，对单独的光谱数据和组合后的光谱数据分类效果进行比较。结果表明，基于组合后的一阶导数谱+二阶导数谱数据构建的PCA+RBF分类模型的分类准确率更高。在对不同类别的重质矿物油样本进行分类时，训练集样本和测试集样本的分类准确率均达100%；在对同种类别下不同品牌的重质矿物油样本分类时，训练集样本误判3个，总体分类准确率达到92.5%，测试集样本的分类准确率均达100%，实验结果最理想。本文提出的光谱数据组合的方法与单独的光谱数据相比，包含了更充分的样本信息，分类准确率更高，且满足法庭科学领域对物证快速、准确、无损的鉴定需求。在下一步的实验中，将对更多种类和品牌的重质矿物油进行研究，进一步探讨光谱组合技术在鉴定重质矿物油物证中的优势，以期实现对法庭科学领域重质矿物油物证的准确鉴别和区分，为光谱组合技术在法庭科学及其他分析测试领域的应用提供一定借鉴。