计算机模拟地质化验室分样及取样常数Ks的估算

江 泓

(福建省地质测试研究中心 福州 350001)

前言

分样是化验室必须的操作之一[1-2]。和其他操作一样，分样也会引入误差。这个误差究竟有多大，不能到项目终结了才知道，必须在项目开始以前有个基本概念。INGAMELLS C O 等[3-5]用统计理论推导出充分混匀的化验室样品，分样时产生的误差R与取样量Wg相关，满足取样方程：

KS=R2W

(1)

式中W为分样量，g；R为相对标准偏差，%：

(2)

其中s为标准偏差，g；Ks为实验室取样常数，单位为g。取样常数Ks与分样的量、误差无关，只与分样时样品的特性有关。样品特性是指粒度大小、粒度分布、矿物解离度等参数。应用取样常数Ks，就可以估算分样Wg时，可能引入的误差；或者根据质量要求，确定最小取样量。在上述的文献中，INGAMELLS等不仅推导了被测物在不同分布下的取样常数，而且介绍了其他估算Ks的方法。杨长山等[6]也讨论了卜松分布下的实验室样品的缩分特征和实验室取样常数Ks的确定方法，他确信和“处于卜松分布下的实验室随机样品，其缩分特性规律Ks=R2·W仍然成立。”。HARVEY D[7]用两个实验证明了取样的重要性，演示Ks的确定步骤。本文试图用计算机模拟简单的二元体系样品的混样和分样过程，考察取样误差(R)与分取的样品重(Ws)、粒度大小(u)之间的关系，进而确定地质化验室取样常数Ks。由于计算机模拟取样是一颗颗的取样，不用预设分布模型；所得的误差不存在分析方法误差和分样操作误差的叠加，完全是因样品本身不均匀产生的。计算机模拟运算速度快，修改参数便利，所得的Ks更接近样品实际。

1 模拟实验

1.1 模拟运算软件

模拟取样采用Visual Basic语言编程。

1.2 模拟样品

取200 g文献[6]中辉石为模拟母样，从中分取一定量样品送消解测定。该样品只含有两种辉石，一种辉石H氧化钾含量较高ω(K2O)=6.00%=xH；另一种辉石L氧化钾含量较低ω(K2O)=0.0114%=xL；样品的氧化钾总含量ω(K2O)=0.0180%=x；样品粒度均为边长0.017 7 cm的立方体。H的密度为dH=3.4 g/cm3；L的密度为dL=3.0 g/cm3。由这些参数推算出其他参数见表1。

表1 样品参数Table 1 Parameters of samples

1.3 模拟混匀样品

两种方式模拟混样。

第一种方式 给12 020 779颗粒样编号，编号从1—12020779。每颗一号。设想这些颗粒随机均匀地混在一起。

第二种方式 设想名义重量为200 g样品构成直角坐标系(x，y，z)中，坐标单位为0.017 7 cm，从点(1，1，1)起到点(229，229，229)的立方体，即该立方体由2293=12 008 989个小立方体组成，每个小立方体的体积均为5.545 233×10-6cm3。用VisualBasic软件中随机函数给坐标(1，1，1)—(229，229，229)的12 008 989个小立方体逐个编号，随机号为1—12 008 989内的整数。每个坐标点一个随机号，对应一个小立方体的起始顶点。然后给随机号为1—11 997 309的小立方体贴上“L”标签；给随机号为11 997 310—12 008 989号小立方体贴上“H”标签。

1.4 模拟分样和测试

测试并不是真将样品送检测室消解，再用适当的方法检测。而是由计算机分别统计两种辉石的颗粒数。

1)对于第一种方式混样后的样品，用Visualbasic软件中的随机函数在1—12 020 779之间随机取整数，模拟取到一颗样品。如果该随机数在1—12 009 088之间，则nL+1，反之，随机数在12 009 089—12 020 779，则nH+1。nH和nL分别为高低两种K2O含量辉石的累计颗粒数。每取一粒样品，计算一次nHxmH+nLxmL=Ws，mH和mL分别为两种辉石的单颗粒重，g；Ws为已取的样品重量。检查Ws是否大于规定的分样量(比如0.5 g)。若小于规定的分样量，则继续按上述步骤一颗一颗地取样，直到Ws大于规定的分样量，计算机即自动停止取样操作。记录最终的nH、nL和Ws。

2)对于第二种方式混样后的样品，用Visualbasic软件中的随机函数在x、y和z三个轴的1—229之间随机取整数，确定分样的起始点。取的样品量由表2中名义样重对应边长的立方体确定。比如，随机确定的顶点坐标为(50，60，70)，名义上取1 g样品，立方体的边长应为39单位。从点(50，60，70)到点(88，98，108)，逐个统计393个小立方体中K2O含量高低两种辉石的个数，即标签分别为”H”和”L”的小立方体个数，记为nH和nL，则分样的实际重量Ws=nHxmH+nLxmL，约1 g样品送消解。

表2 分样重与对应立方体边长关系Table 2 The relations between weght of sub-samples and side-length of corresponding cubics

1.5 模拟检测结果计算

按上述方法分取0.1～100 g 16种重量的样品，每种重量各分别实验20次，共20×16=320个样品。每个样品根据下式计算样品中K2O的含量

(3)

统计每种重量20次实验的K2O含量的平均值，方差和相对方差平方R2。作出16组样品的R2-Ws图。

2 结果与讨论

2.1 R2-Ws图

第一种混匀取样的R2-Ws图如图1所示。

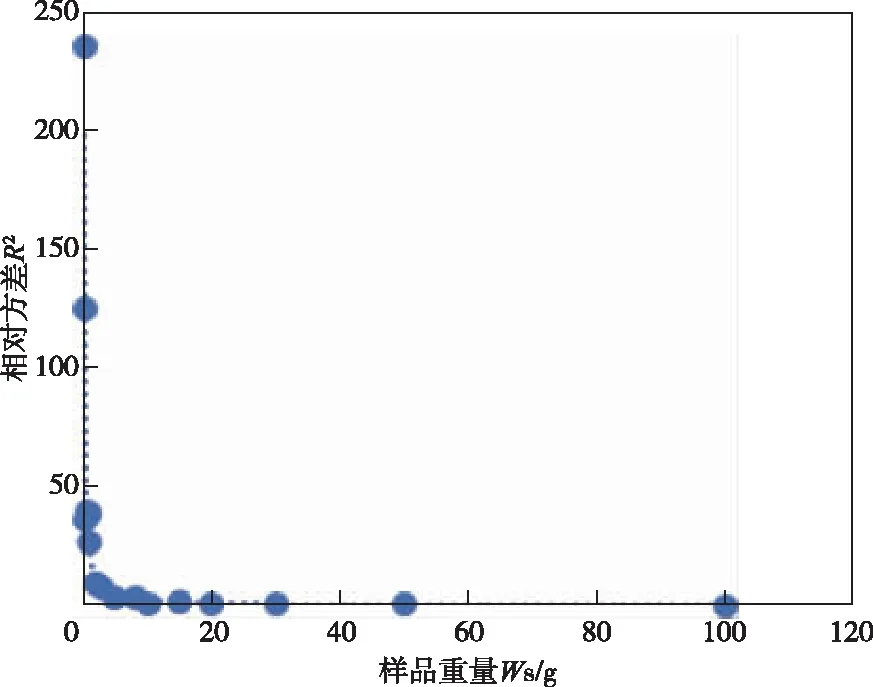
图1 模拟样品Ws-R2关系图Figure 1 Diagram of Ws-R2 of simulated samoles

图1可见，从样品粒度为0.017 7 cm每种重量20次实验结果统计的R2对Ws作图，用指数函数进行拟合，获得：

(4)

R2=0.975 5。基本上与Ingmalls的取样方程相符。由此估算取样常数Ks=21.15 g。重复模拟这个实验8次，统计结果如表3所示。

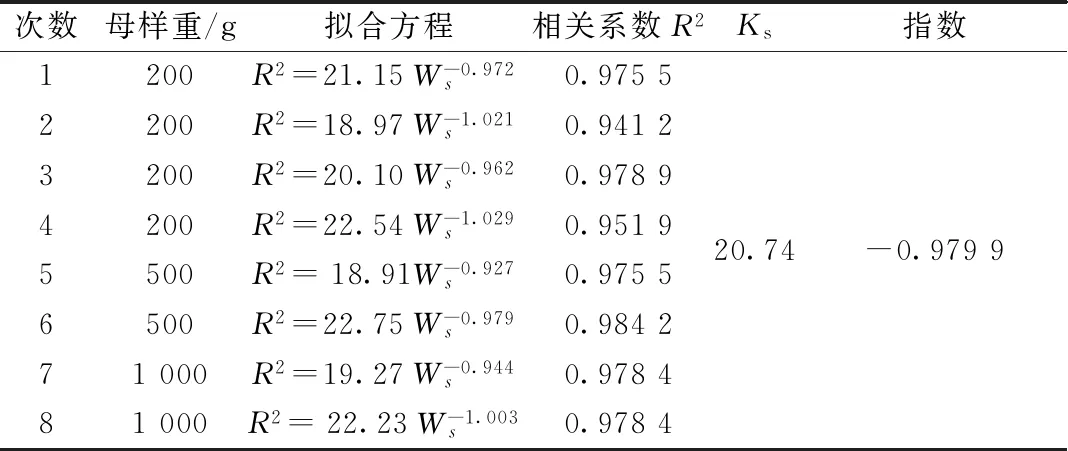
表3 8次模拟实验结果Table 3 Results of 8 tests

表3中可见，模拟实验结果还是比较稳定的，平均的取样常数Ks=20.74 g，比文献[6]计算和文献[1]的数据略低。这可能是由于文献中忽略了分析误差所致。模拟实验是一颗颗统计样品含量，因此没有分析过程带来的误差，误差的唯一来源是样品本身的不均匀特征。

表3中第5—8次实验是考察不同母样量的影响。表3中可见，无论是从200 g母样还是从500 g或1 000 g母样中分取子样，所得的取样方程没有显著差异。

2.2 两种混匀取样方式比较

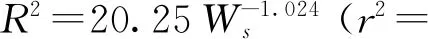
2.3 不同样品粒度的取样方程

上面考察的样品粒度单位均是0.017 7 cm。图2是模拟取粒度u为0.1、0.084、0.049、0.025、0.017 7、0.014 9、0.009 3、0.007 4 cm 8个粒级样品，作出的lnWs-lnR2图。

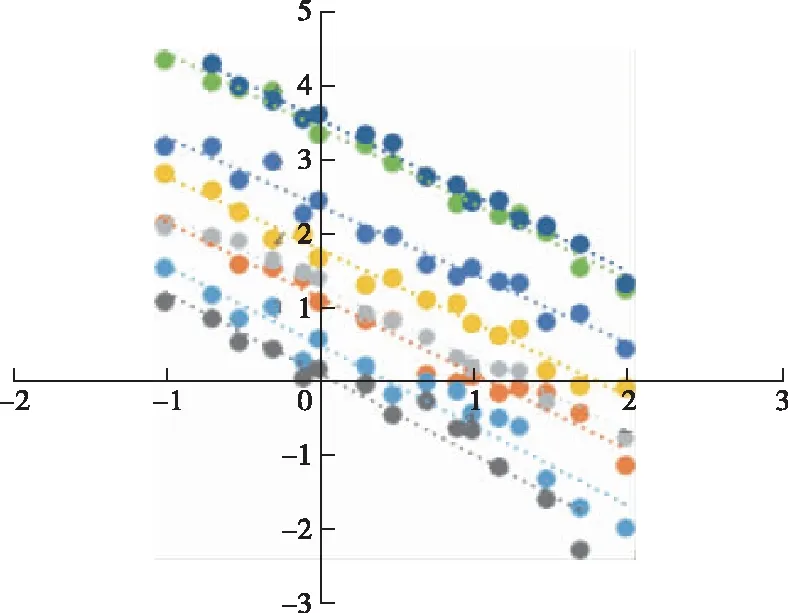
图2 不同粒度下的lnWs-lnR2关系Figure 2 A diagram of lnWs-lnR2different graim sizes.

回归方程见表4。

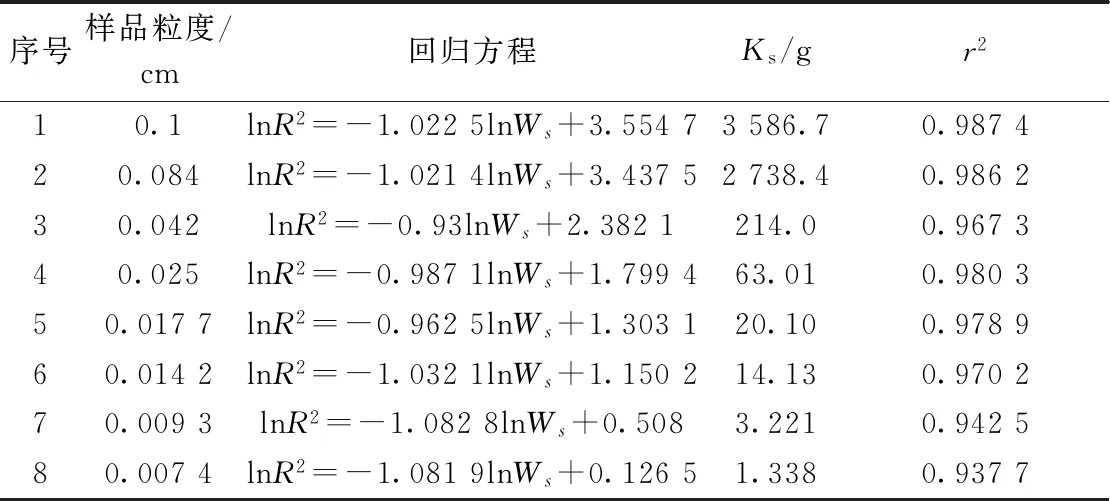
表4 不同粒度模拟样品的lnWs-lnR2关系Table 4 lnWs-lnR2 for different grain size

图2和表4可见，在地质化验室常见的样品粒度范围内，各粒度分取样品量Ws与相对误差的对数关系，也符合Ingamells的取样公式。相关系数均达0.9以上。表4 中还可看出，Ks对样品粒度的立方u3(U代表样品粒度，单位为cm)有极佳的线性关系。

lnWs=1.003 2lnu3+6.604 5

(5)

R2=0.997 3。也与Ingamells推导的Ks计算公式相符。由⑸式可以估算其他粒度的取样常数，比如，0.012 5 cm，Ks=7.53 g。

实验中也发现，当样品粒度比较粗时，比如0.084 cm或0.1 cm，同时取样量比较少，比如0.1 g或0.2 g时，有时出现精密度特别高的现象，甚至20次实验的方差为零，偏离了Ingamells取样方程。该现象与文献[4]所述的一样。因为样品颗粒比较粗时，H的颗粒很少，取样量太少时，经常取不到，以致检测结果趋近L含量，结果严重偏低，不能反应样品的真实状况。因此将这些点剔除。

2.4 小于0.007 4 cm粒度样品模拟实验

在上面模拟实验中，观察到在模拟粒度比较细的样品时，比如小于0.01 cm，分取样品量占母样的比例越大，比如50 g和100 g样时，标准偏差s值突然变小，偏离上述规律，以致回归直线的斜率有变大趋势。当进行0.004 4 cm样品模拟时，斜率甚至大至-1.7，完全偏离了Ingamells取样方程。可见前面认为取样误差与母样量无关的观点，不适用于极细，且分取的样品量与母样量比较大的样品。可能因为：1)极细的粉末样品性质发生了突变；2)取样量太大，分取的样品接近母样，分析结果接近平均值。这个推测需进一步验证。通常地质化验室测试用样品最小的粒度是0.007 4 cm，且取样量与母样相比往往可能忽略不计，都在我们实验的范围内，不会偏离Ingamells取样规律。

3 实践应用

将公式(1)作对数变换得：

lnR2=-lnWs+lnKs

(6)

将上述推算得的各粒级的Ks和相应的Ws代入(6)式，作出地质化验室内取样的诺模图，如图3所示。横坐标是取样量Ws的对数值，纵坐标是相对方差R2的对数值。A、B、C、D、E和F分别是粒度为0.025、0.017 7、0.014 9、0.012 5、0.009 3 cm和0.007 4 cm的Ws对R2的诺模曲线。应用诺模图可以估计取样的误差，也可依据规定的质量要求，确定样品粒度和最小取样量。

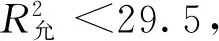
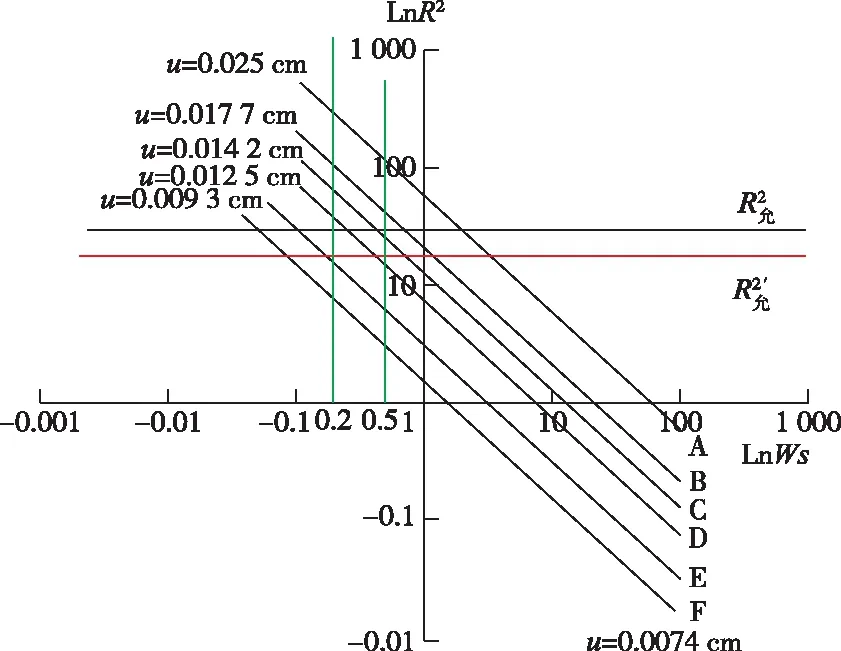
图3 化验室取样的模诺图Figure 3 A nomograph of laboratory sampling

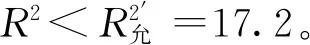
4 结论

1)经过与Ingamells取样方程比较，计算机模拟取样过程同样可以反映取样规律。但计算机模拟不须设定样品分布规律，而且计算机运算速度快，参数变换方便，也没有分析误差和样品制备误差干扰，可用于生产实际。推测如果增加参数，比如：增加粒度分布，解离度等参数，使模拟更接近实际状态也是可行的。

2)模拟实验发现对于粒度小的样品，如<74 μm，特别当取样量占母样量比例大时，Ingamells取样公式不适用。这类样品的取样规律还需进一步探索。

3)计算机模拟取样可用于制定项目取样操作细则。毕竟本法也只是模拟，不是实际操作过程，因此只可用于初步评估取样质量。实际测试结果质量评估还得依靠检测质量保证体系。