Target maneuver trajectory prediction based on RBF neural network optimized by hybrid algorithm

XI Zhifei,XU An,KOU Yingxin,LI Zhanwu,and YANG Aiwu

Aeronautics Engineering College,Air Force Engineering University,Xi’an 710038,China

Abstract: Target maneuver trajectory prediction plays an important role in air combat situation awareness and threat assessment.To solve the problem of low prediction accuracy of the traditional prediction method and model,a target maneuver trajectory prediction model based on phase space reconstruction-radial basis function (PSR-RBF) neural network is established by combining the characteristics of trajectory with time continuity.In order to further improve the prediction performance of the model,the rival penalized competitive learning (RPCL) algorithm is introduced to determine the structure of RBF,the Levenberg-Marquardt (LM) and the hybrid algorithm of the improved particle swarm optimization (IPSO) algorithm and the k-means are introduced to optimize the parameter of RBF,and a PSR-RBF neural network is constructed.An independent method of 3D coordinates of the target maneuver trajectory is proposed,and the target manuver trajectory sample data is constructed by using the training data selected in the air combat maneuver instrument(ACMI),and the maneuver trajectory prediction model based on the PSR-RBF neural network is established.In order to verify the precision and real-time performance of the trajectory prediction model,the simulation experiment of target maneuver trajectory is performed.The results show that the prediction performance of the independent method is better,and the accuracy of the PSR-RBF prediction model proposed is better.The prediction confirms the effectiveness and applicability of the proposed method and model.

Keywords:trajectory prediction,k-means,improved particle swarm optimization (IPSO),Levenberg-Marquardt (LM),radial basis function (RBF) neural network.

1.Introduction

Air combat target maneuver trajectory prediction is the process of learning historical trajectory of the target,and the trained model is used to predict the future maneuver trajectory of the target [1].With the increasingly complex air combat environment,the intensification of electromagnetic confrontation,and the improvement of the performance of precision guided weapons,it is very important to accurately predict the target maneuver trajectory.On the one hand,our own future trajectory information can be sensed in advance,and then air combat situation can be analyzed and judged,so as to make reasonable maneuvering decisions and avoid safety accidents[2].On the other hand,in the fierce process of air combat confrontation,the target maneuver trajectory is accurately predicted,which can effectively guide the fighter to occupy the position,gain situation advantage and improve the possibility of winning the air combat [3].Therefore,it is of great significance to study target maneuver trajectory prediction.

The air combat target maneuver trajectory is essentially a time series prediction problem,and the prediction problem is highly nonlinear,complex and time-varying.Recently,the prediction methods of target maneuvering trajectory can be divided into two categories:parametric method and nonparametric method.Parametric methods mainly include particle motion,linear and nonlinear parameter regression,Kalman filtering algorithm,α/β filtering algorithm and other prediction methods.Based on the classical parametric prediction method,a variety of improved target trajectory prediction models are constructed.For example,the basic flight model is proposed to predict the track [4];the track of the moving target is predicted by combining the prediction model of target acceleration,the track deflection angle and the historical track[5];the continuous prediction of track position is realized by using the dynamic Kalman filter [6];an improved adaptive particle filter algorithm is proposed to predict the trajectory of civil aviation aircraft [7].Because the prediction accuracy of single model estimation is poor and the complexity of the multiple model algorithm is high,in order to modify the deficiency,an interactive multiple model algorithm was proposed in [8].For the target with a relatively simple motion process,the prediction performance of the above method is high,while the motion of the aircraft is a complex and variable nonlinear time series process,and affected by a variety of factors.The traditional prediction model is difficult to describe all the information of the motion,and the model complexity is high,the adaptability to the target movement diversity and uncertainty is poor,and it is relatively difficult to improve the accuracy of the trajectory prediction [9].

Nonparametric methods mainly include various neural network prediction methods.For example,the target group track is used to train the back propogation (BP)neural network,and the track prediction model is established to realize the prediction of the flight track in advance [10].However,the BP neural network is highly dependent on the initial value and the ability of global search is poor.In order to solve these problems,the genetic algorithm and the particle swarm optimization(PSO) algorithm with global search ability are used to optimize the neural network weights,so as to improve the prediction accuracy [11,12].In addition,the essence of trajectory prediction is time series prediction with the characteristics of high nonlinearity and time-varying.The traditional BP neural network is static feedforward neural network,this can only realize the static nonlinear mapping relationship,so that the accuracy of trajectory prediction is relatively low.In order to solve the problem of poor dynamic performance of traditional neural network,a prediction method based on nonlinear autoregressive with external input (NARX) neural network is proposed[13].This above method does not need to establish the motion model,the prediction is real-time,but the neural network is easy to fall into the local optimum in the training process,and the training data is less in general,the prediction results are not convincing.To sum up,it is an urgent problem to find a fast and accurate method to predict the target maneuver trajectory.

The radial basis function (RBF) not only has a local approximation performance and a best approximation performance,but also has a good convergence ability,generalization performance,robust performance,etc.The PSO has a strong global convergence ability and a strong robustness.As a simple and effective random search algorithm,the PSO has been studied and shows that it has great potential in optimizing neural networks.Combining the two can not only improve the generalization performance and robust performance of the radial basis neural network,but also improve the learning ability and convergence speed of the neural network.The PSO enables the RBF network to obtain more superior convergence performance and a lower error rate,but the PSO also has some inherent deficiencies,the algorithm is easy to fall into local extreme values,and the late convergence speed is slow.Therefore,in order to improve the performance of the PSO algorithm in optimizing RBF,a hybrid optimization algorithm is proposed.The main contributions are summarized as follows.

(i) Improve the standard PSO algorithm.The dynamic adaptive inertia weight strategy,the dynamic adaptive flight time factor and the chaos mutation strategy are used to modify the standard PSO.

(ii) Determine the structure of the RBF neural network.In this paper,phase space reconstruction (PSR) is developed to determine the model input.Furthermore,the C-C method is applied to determine the key parameter of the PSR.Then the rival penalized competitive learning(RPCL) is used to determine the number of hidden neurons in the RBF.

(iii) Optimize the parameters of the RBF neural network.The hybrid algorithm of improved PSO (IPSO) and k-means is used to optimize the center of the basis function,and then the Levenberg-Marquardt (LM) algorithm is used to optimize the width of the basis function and the weight.

(iv) Construct a scientific and reasonable evaluation system.Model checking and four evaluation indices are introduced.

The rest of this paper is arranged as follows.Section 2 and Section 3 describe the preprocessing methods in detail.Section 4 gives the structure of the proposed prediction model.Two experiments and the discussions are shown in Section 5.Finally,Section 6 gives the conclusions.

2.PSR

PSR is an efficient method for analyzing nonlinear time series [14,15].The basic principle is to reconstruct the low dimension time series into high-dimensional phase space to solve the problem.

The time seriesx={x1,x2,···,xN},the embedding dimension ism,and the delay time ist,then the set of time series reconstructed by phase space can be expressed as

whereM=N−(m−1)t,Xi(i=1,2,···,M) is the point in phase space.

The key to PSR is to determine the optimal embedding dimensionmoptand optimal delaytopt.In this paper,the CC method [16]is used to determine the optimal embedding dimensionmoptand time delaytoptsimultaneously.Based on (1),the associated integral is defined as

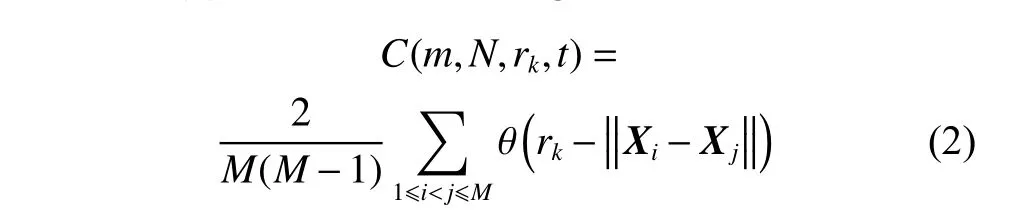
whereNis the length,rkis the neighborhood radius,θ(x)is a Heaviside unit function and it is expressed by

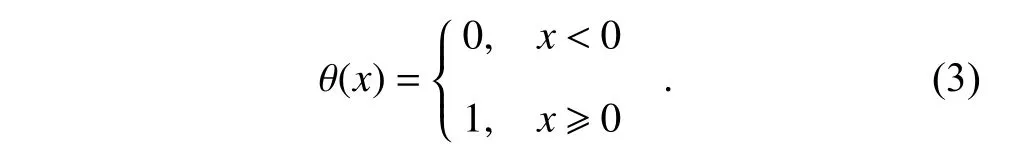
According to Brock Dechert Scheinkman (BDS) statistical conclusions[17],whenN>3 000,the range of values ofmandrkcan be obtained,m∈{2,3,4,5},rk=k×0.5σ,where σ is the standard deviation of the time series andk∈{1,2,3,4}.

Based on the matrix partitioning average strategy,the test statisticsSis defined as

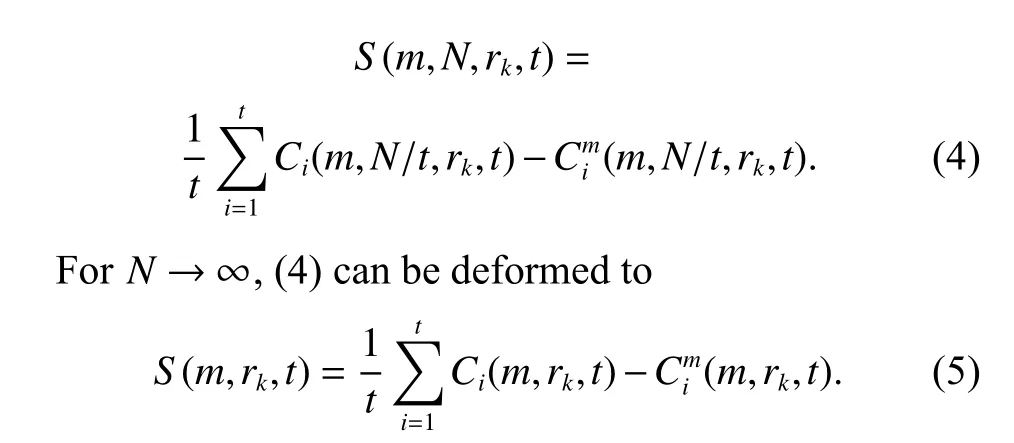
For the fixedmandt,S(m,rk,t) will be equal to 0 for allr,if the data are infinite andN→∞.However,the real data set is not infinite,and there may be a correlation between data.Thus,the optimal delay time may be either the zero crossing ofS(m,rk,t) or show the least variation withr.

To represent the variation ofS(m,rk,t) withr,the test statistics ∆Sis defined as

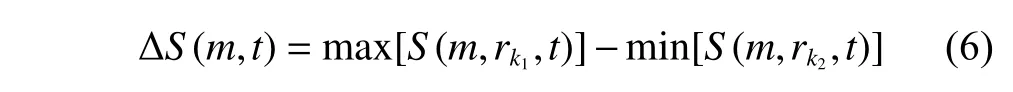
where,k1∈{1,2,3,4},k2∈{1,2,3,4}.

The means ofSand ∆Sare defined as,and the equations are defined as

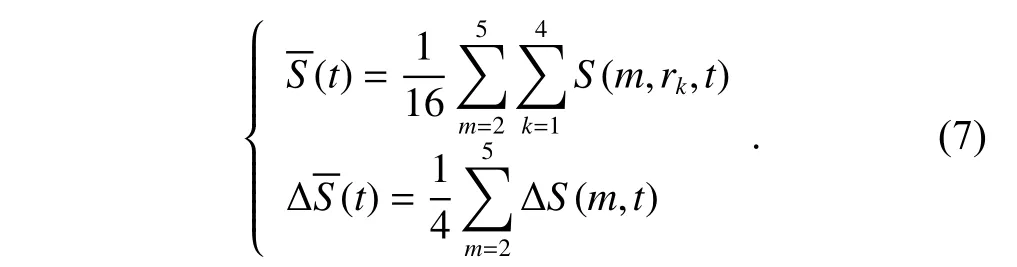
For all values oft,can find corresponding values,where the valuetcorresponding to the first zero point of or the first minimum point ofor the first minimum point ofis rounded to be the optimal delaytopt.

The test statisticalScoris defined as

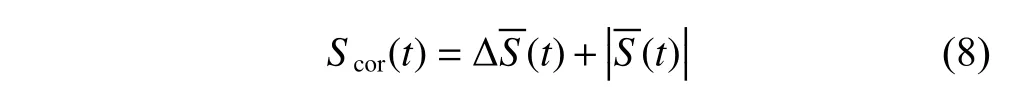
where the valuetcorresponding to the global minimum point ofScor(t) is the optimal embedded windowtw.

When the optimal delaytoptis determined by (7) and the optimal embedded windowtwis determined by (8),the optimal embedding dimensionmoptcan be determined by rounding the value of (9).

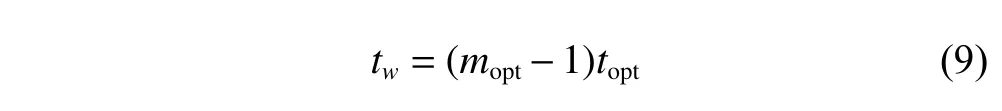
3.Hybrid algorithm of IPSO and k-means clustering algorithm

The advantages of the k-means clustering algorithm are fast convergence and strong local search ability,but the clustering results are easily affected by the initial clustering center.Different initial center points may cause different clustering results,and the obtained results are unstable and volatile.The algorithm often cannot obtain the optimal solution,and it is easy to fall into the local optimal solution.

In view of the above problems,at present,another method is mainly used to optimize it,and the obtained result is used as the initial condition of the k-means clustering algorithm [18].The evolutionary algorithm has an excellent global optimization ability,so many researches apply it to optimize the initial clustering center of the kmeans algorithm.

Compared with other evolutionary algorithms,the PSO algorithm has the advantages of fast convergence speed,high efficiency,simplicity,easy implementation and fewer parameters to be set and adjusted.PSO can also solve many optimization problems that other evolutionary algorithms can solve,and PSO will not degenerate.In addition,PSO has the memory ability that the genetic algorithm does not have.The change of population in the genetic algorithm may destroy the previous knowledge and experience.However,in the PSO algorithm,all particles can retain the memory of knowledge and experience about the optimal solution.

Therefore,combining with PSO and the k-means algorithm,the global search capability of the PSO can be used to optimize the initial clustering center of the kmeans algorithm.The randomness of the PSO in the solution space can effectively avoid the k-means algorithm falling into the local optimal solution.Although PSO has a strong global search ability,in the process of global search,it may still cause premature phenomenon and fall into local extremum.

Based on the above analysis of the algorithm,when the PSO is combined with the k-means algorithm,in the process of using the excellent global searching ability of PSO to search the global optimal initial clustering center of the k-means algorithm,the following problems need to be considered and solved:

(i) The different combinations of the two algorithms and the different conversion timing will have different effects on the efficiency and performance of the algorithm.When the two algorithms are combined,the problem of how to choose the appropriate combination method and conversion timing needs to be considered;

(ii) In the process of global search,PSO may fall into a local extreme value due to the premature phenomenon,so it is necessary to solve the problem of premature convergence of PSO.

Based on the above analysis,a k-means clustering algorithm based on the IPSO is proposed in this paper.In the former part of the algorithm,the IPSO is executed,and the k-means algorithm is executed in the latter part of the algorithm,and the conversion timing of the two algorithms is designed.

3.1 IPSO

The basic PSO has some inherent shortcomings.In the process of optimization,the algorithm may fall into local extremum.When the particles fly in the solution space,the inertia weight and the time of flight factor are constant,but in the practical application,the values are always changing.Therefore,in order to solve these problems,the algorithm proposed in this paper monitors the optimal value of each particle and particle swarm in real time,mutates the premature particle,increases the diversity of the particle swarm,and makes it jump out of the local optimal solution in time.At the same time,the inertia weight and the time of flight factor are dynamically adjusted to enhance the search performance of PSO.

In this paper,the combination of the two algorithms makes up for the deficiency of the global search ability of the k-means algorithm,eliminates the dependence of the k-means algorithm on the initial value,improves the slow convergence of PSO in the later stage,accelerates the convergence speed of PSO,and improves the accuracy of clustering results.The specific design of the algorithm is described in detail below.

3.1.1 Dynamic adaptive inertia weight

The inertia weigh ω as a control parameter has a great inlarge inertia weight ω can effectively accelerate the conweight ω can effectively improve the convergence accufluence in the performance of the PSO algorithm.The vergence speed of the algorithm,while the small inertia racy of the algorithm.Compared with the linear inertia weight,the nonlinear inertia weight has more advantages.Because there is a larger ω in the initial stage so that all particles can quickly spread in the search space,so as to determine the approximate range of the global optimal,while there is a smaller ω in the later,so that the particles can determine the global optimal value.Therefore,average particle spacing (APS) is used as a guideline to adjust the inertial weight in this paper [19].The dynamic adaptive inertia weight can be expressed as

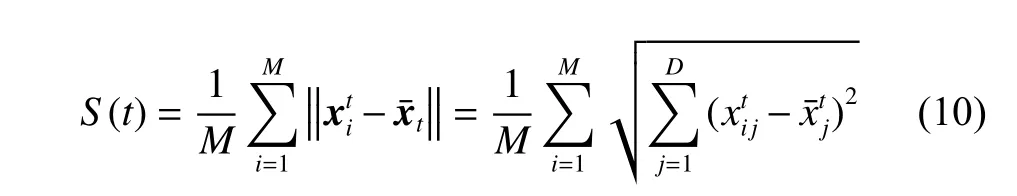
wheretis the current number of iterations,MandDrepresent the population size and the spatial dimension respectively,is the current spatial position vector of the particlei,is thejth position component of the particlei,is the current average spatial position vector of the population,andis thejth average position component of the population.In this paper,the nonlinear inertia weight can be described as

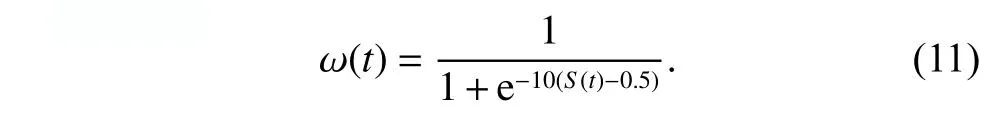
When the value of APS is large,the nonlinear inertia weight tends to the maximum.When the APS is small,the nonlinear inertia weight is close to the minimum value,and the intermediate process passes through an approximate linear transition.The inertia weight designed by the APS facilitates the PSO algorithm to obtain the optimal solution with a faster convergence rate.

3.1.2 Dynamic adaptive time of flight factor

Some studies found that in the actual situation,when the particle position changes,not only the speed is constantly changing,but also the actual flight time is constantly changing.In the position updating formula of the basic PSO algorithm,the coefficient of the velocity term is fixed,and the flight time of each particle is fixed,this will cause the particle to oscillate around the optimal solution and cannot converge to the optimal solution.Therefore,the time of the flight factor is introduced to accelerate the convergence of the PSO algorithm in this paper.The particle’s position update formula can be changed to

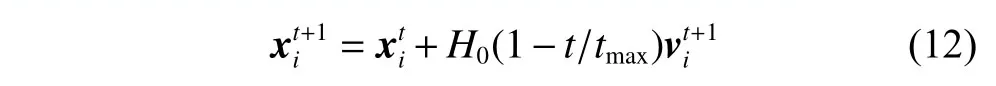
whereH0is the flight constant,andtmaxis the maximum number of iterations.

3.1.3 Chaotic mutation

Chaos is a stochastic,ergodicity,dynamic,deterministic,nonlinear and non-repetitive system that demonstrates a sensitive dependence on the initial conditions and also includes infinite unstable periodic motions [20,21].Due to the nature of ergodicity,mixing properties of chaos,and non-repetition nature,it potentially carries out overall search at higher speeds than the stochastic ergodic search that is probabilistic in nature.Various researchers [22,23]integrated the chaotic systems with the optimization algorithms to enhance the search capability and prevent them from being trapped at the local minima solution.

In this paper,the chaos mutation operator is introduced to guide and improve the direction of particle search.The basic idea of chaos mutation operation is to map optimization variables into the value region of chaos variable space through chaos mapping rules,and then the ergodicity and regularity of chaos variables are used to search for an optimal solution,and finally the obtained optimal solution is linearly transformed into optimization space.The process of chaos mutation is as follows:

where α is the parameter used to control the scale of chaos variation,and the parameter λ is used to control the speed of scale contraction.

Considering the strong ability of global searching,and jumping out of the local extremum in the early stage of the algorithm and the strong ability of local searching and fine searching in the later stage of the algorithm,a gradual chaos mutation search method is proposed.Firstly,the basic PSO algorithm search strategy is used to search the global solution and narrow the search range;then,the search strategy of the chaotic mutation PSO algorithm is used to perform local search to complete the deep search.Therefore,the key of chaos mutation is to determine the time of mutations,the control variable δ is proposed to solve the problem in this paper.The process of chaotic mutations is shown in Fig.1.

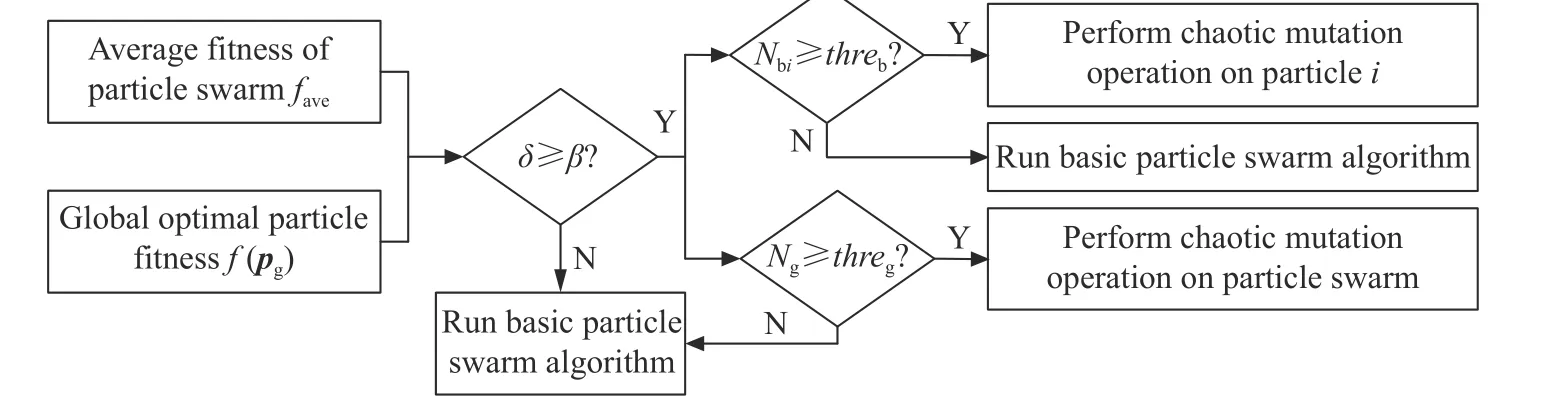
Fig.1 Flow chart of determining chaotic mutation timing

wherexiis the position of particlei,f(xi) is the fitness of particlei,faveis the average fitness of the particle population,is the current optimal solution of particlei,pgis the current global optimal solution,Npiis used to monitor the change of the optimal value of particlei,Ngis used to monitor the change of the optimal value of particle swarm.

End procedure

In this paper,the chaos mutation operator is introduced,which uses the diversity of particles,and the number of stagnation steps of each particle optimal value and the global optimal value as the trigger condition of mutation.The chaotic mutation operator is used to chaotically mutate the particles to guide the search direction of the particles so that they can jump out of the local optimal solution,thereby effectively avoiding the occurrence of premature convergence.The chaotic mutation strategy of the algorithm is described in Algorithm 1.

3.1.4 Design for algorithm switching timing

In order to make full use of the global search ability of PSO and the local search ability of the k-means algorithm,and accelerate the convergence speed of PSO in the later stage,the convergence time of PSO is regarded as the best switching time of the algorithm in this paper.The convergence degree of the particle swarm can be reflected by the fitness variance,and the fitness varianceσ2can be defined as

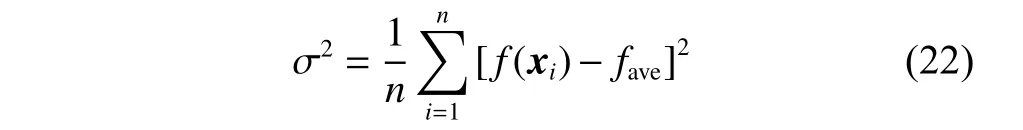
wherenis the population size of particle swarm,f(xi) is the fitness of particlei,andfaveis the average fitness of particle swarm.When the fitness variance σ2is close to the thresholdthresholdσ,it shows that the fluctuation of the fitness value of particle swarm is very small,and the state of particle swarm tends to convergence.This means that even if the algorithm continues to perform iterative calculations,the optimization results cannot be improved to a great extent,resulting in an increase in calculation time,so this is the best time to switch the algorithm.

3.2 Flow of hybrid algorithm of IPSO and k-means

The concrete flow for the proposed algorithm is depicted in Fig.2.

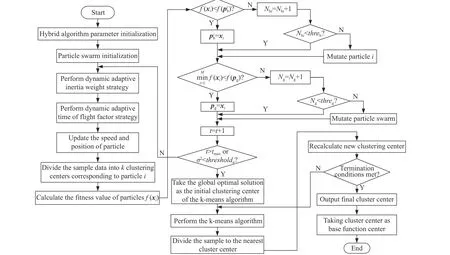
Fig.2 Flow chart of determining chaotic mutation timing

4.Design of target trajectory prediction algorithm based on k-means clustering combined with RPCL algorithm for RBF neural network (RBFNN)

The main work of RBFNN target trajectory prediction model is to construct a neural network prediction model suitable for the air combat counteract environment.The task is divided into two steps.Firstly,in the offline training phase,the main work is to train the best RBFNN predicting model.Secondly,in the prediction phase,the received target data obtained in real time is input to the trained RBFNN,thereby the future trajectory of the target will be predicted.

This paper is based on the RBFNN,this is a three-layer feedforward NN,and it has an ability of approaching random non-linear function and dealing with any irregular data problems.The RBFNN has a broad application prospect in time sequence prediction.In addition,the RBFNN is a local approximation,this learning convergence rate is faster than the BP NN [24].The network also has an excellent learning ability,a generalization ability and a fast training speed.The prediction model of target maneuver trajectory based on RBFNN is as follows.

The phase space reconstruction theory is adopted to process the target maneuver trajectory time series to determine the optimal embedding dimensionmand the optimal delayt,then the input vectorof neural network is obtained,whereXk+1−mis themth dimension data after phase space reconstruction.Fig.3 shows the RBFNN of the target maneuver trajectory prediction model.

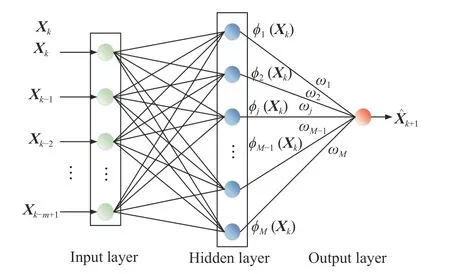
Fig.3 Structure of RBF prediction model

In the target maneuver trajectory prediction model,since the original load data is input to RBF after PSR processing,the number of the input layer neurons of RBF can be directly set to embedding dimensionsm.The purpose is to construct a more stable and better RBF target maneuver trajectory prediction model.The input sample data needs to be preprocessed,that is,normalized.

The second layer is a hidden layer,and the number of neurons is determined by the actual application requirements.In this paper,we choose the Gaussian function as the RBF of each neuron in the middle layer,because the Gaussian function is a positive definite function in any dimensional space and has a unique solution.The formula is as follows:

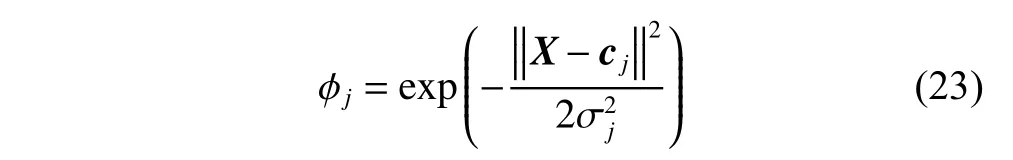
whereσjisthe basewidthof hiddenlayernodesandbiggerthan zero,cjis thecenter vectorof thejthnode inthe RBF network hidden layer,cj=[cj1,cj2,···,cjn],j=1,2,···,m.

The third layer is the output layer.In this network model,the connections between the input and intermediate layers are usually weightless.Usually,only the signal is passed to the hidden layer,and the weight between the intermediate layer and the output layer isW=[ω1,ω2,···,ωm]T.The output formula of the final output layer neuron is as follows:

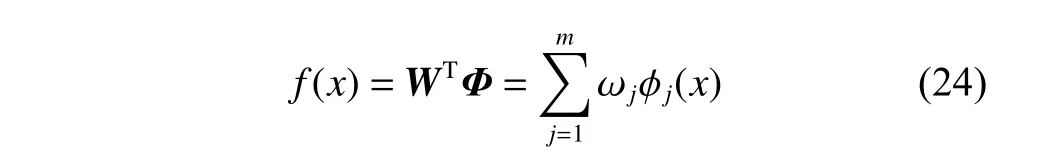
wheref(x) is the output of the neuron in the output layer and ωjis the weight between thejth neuron in the middle layer and the neuron in the output layer.

In this paper,we design the RBFNN for target maneuver trajectory prediction.The design here is mainly divided into two steps:the first step is to determine the structure of the RBF prediction model.The main task of this step is to determine the number of hidden layer neurons based on the RPCL [25]and initialize the parameters.The second is to use an appropriate algorithm to optimize and adjust the parameters of the neural network.The parameters include the centercof the hidden layer neuron kernel function,the width σ,and the connection weight ω.The purpose of these design steps is to construct an optimal prediction model.Fig.4 shows the design flow of the RBFNN.

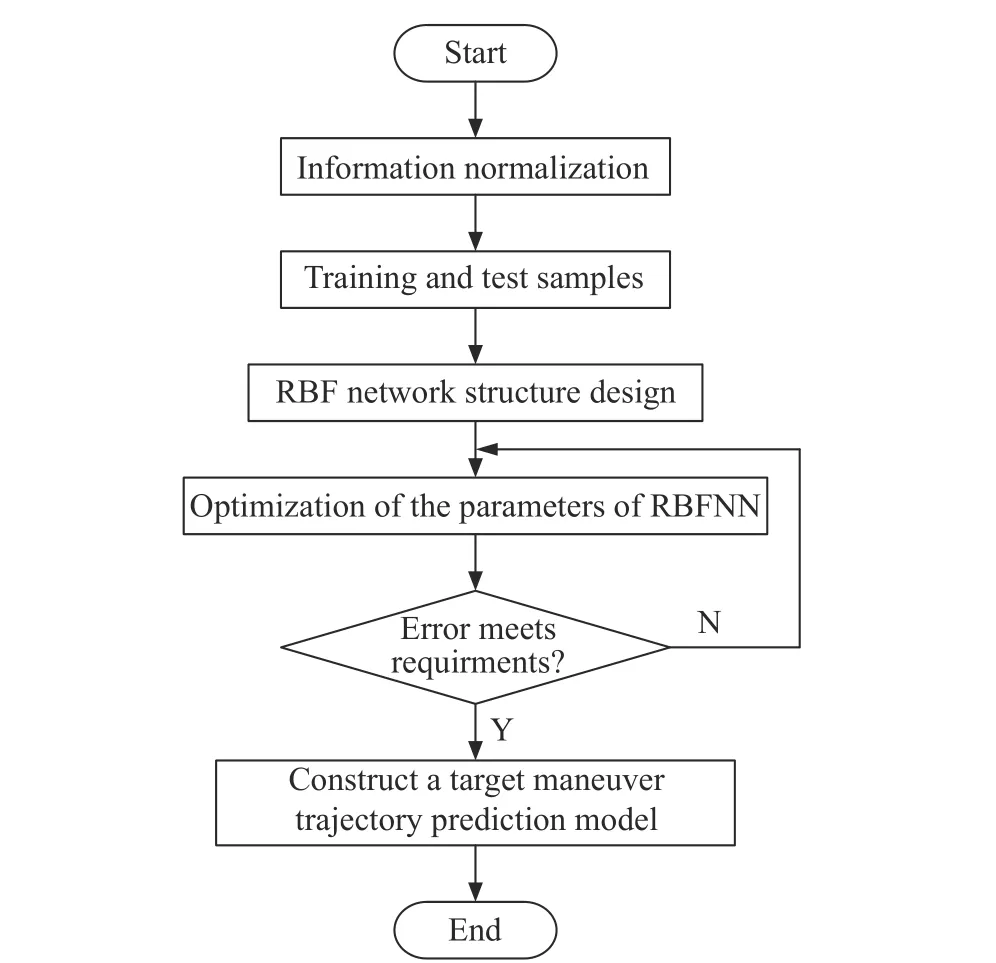
Fig.4 Flow chart for the design of RBFNN

4.1 RBFNN structure design based on RPCL algorithm

For the RBF,the number of neurons in the hidden layer has a significant effect on the prediction result.Too few neurons in the hidden layer will cause insufficient fitting to affect prediction performance,and too many neurons in the hidden layer will cause over-fitting and make prediction performance worse.Therefore,in order to improve the prediction accuracy of the RBF,the RPCL is used to design the RBF structure.

The basic idea is that for each input not only the winner unit is modified to adapt to the input,but also its rival is delearned by a smaller learning rate.RPCL can be regarded as an unsupervised extension of Kohonen’s supervised learning vector quantization 2 (LVQ2).RPCL has the ability of automatically allocating an appropriate number of units for an input data set.The RPCL is applied to the problems of RBF network training in this paper.

SupposeNinputs,x1,x2,···,xN,come fromkunknown clusters.Then the RPCL algorithm randomly initializeskseed pointsm1,m2,···,mk,and adaptively updates them so that thosextcan be correctly classified based on the indicator function:

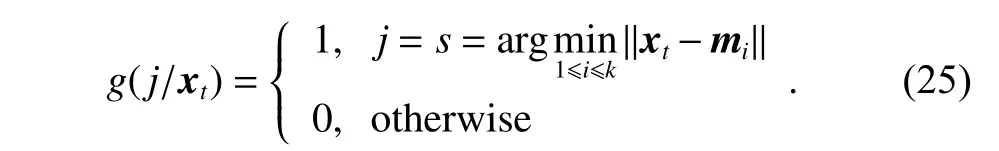
That is,xtis divided into thejth cluster ifg(j/xt)=1.The main idea of RPCL to update the seed points is that for each input sample,not only the winning seed pointmc(i.e.,g(s/xt)=1)is modified to adapt to the input,but also its nearest rival is delearned by a smaller learning rate.Specifically,the RPCL algorithm is used to determine the structure of RBF,which consists of the following four steps [26]:

Step 1Randomly take a samplexlfrom the sample data setand fori=1,2,···,k,where

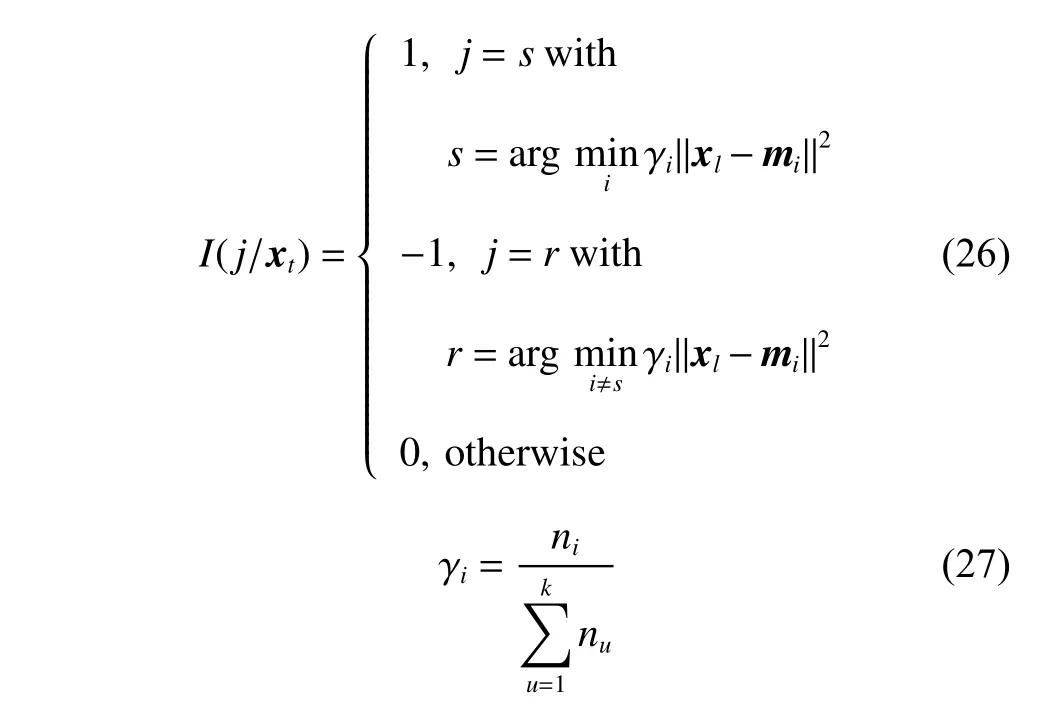
whereniis the cumulative number of the winning occurrences ofmiin the past.

Step 2Update the seed pointmcby

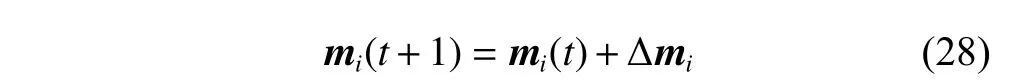
where ∆miis the magnitude by which thecth seed point is adjusted when thelth input vector is applied to the network and is determined as follows:

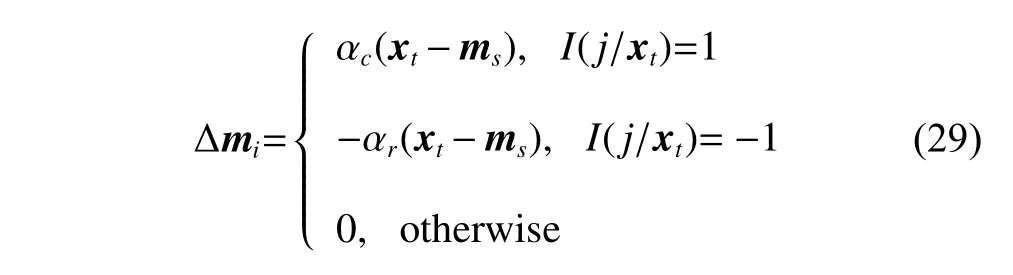
where αcand αrare the learning rates of the winner and rival respectively.

When the conditionI(j/xt)=1 is satisfied,the cumulative number of each center becoming the winning node can be calculated as

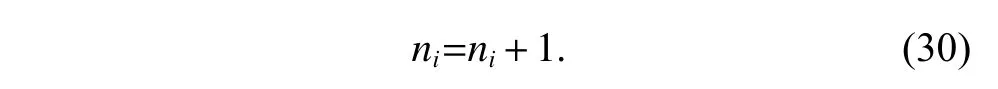
The above two steps iterate for each input until a stop criterion is satisfied,for example,the iteration number reaches the preassigned maximum value,or absolute difference between the consecutive classification errors is smaller than a preassigned threshold value.

Step 3Count the cumulative number of each center becoming the winning node.If the value is smaller than the threshold δ(for deleting redundant items),delete the node.

Step 4Output the optimal number of hidden layer neurons and the center vector of each neuron.

The RPCL algorithm makes the RBFNN more compact,and improves the training speed through determining the appropriate number of hidden layer nodes.

4.2 Optimization of initial parameters of RBF based on hybrid algorithm

The topology of RBF has a great impact on its network performance.Before selecting parameters of RBFNN,the number of neurons in the hidden layer must be determined.Then,the performance of RBF depends on the selection of network parameters,that is the basis function centerc,basis function width σ,and output layer weight ω.

In this paper,the RPCL algorithm is used to determine the number of hidden layer neurons of RBFNN.At the same time,the k-means modified by the IPSO and the LM algorithm are used to optimize the RBF parameters.The optimization process can be divided into two parts.First,the basis function center of the basic function is optimized by the improved k-means clustering algorithm.Then the basis function width and output layer weight are determined by the LM algorithm.The other is to optimize the basis function width σ and output layer weight ωon the basis of the LM algorithm.The optimization process of RBF parameters can be described as follows:

Step 1Initialize algorithm parameters.Randomly selectkclustering centers from the given training samples as the initial positionsxiof particles.The optimal positionfor each particle,global positionpgin the swarm,and particle velocityviare initialized.

Step 2Run the IPSO algorithm.Perform the dynamic adaptive inertia weight strategy,dynamicadaptive time of flight factor strategy,and chaotic mutation strategy.

Step 3Calculate the fitness variance of the particle swarm to determine whether the algorithm switching conditions are satisfied.If the conditions are satisfied,Step 4 is executed,otherwise,Step 2 is continued.

Step 4Perform the k-means clustering algorithm to obtain the final basis function centerc.

Step 5Perform the LM algorithm to optimize the basis function width σ and the output layer weight ω.

4.3 Procedure of the PSR-RBF prediction model

For the list of target maneuvering trajectory historical data time seriesX={X1,X2,···,XN},the construction process of the PSR-RBF prediction model is as follows:

Step 1Normalization.The time series of the target maneuvering trajectory is normalized to prepare for the training of RBFNN,and the maximum and minimum values of the data are saved for subsequent denormalization of the predicted value of the target future maneuvering trajectory to restore the real value.

Step 2PSR.The C-C method is used to process the target maneuver trajectory time series,then the optimal embedding dimensionmand optimal delay timetof the time series are obtained,and the time series is reconstructed.The time series is reconstructed as follows:

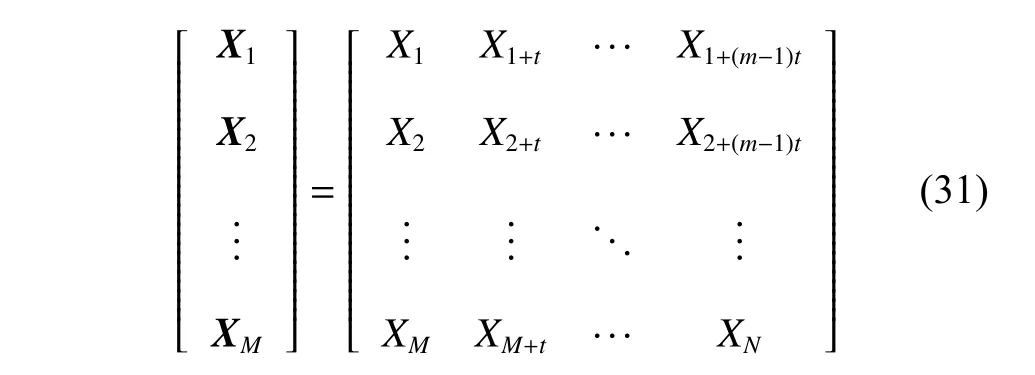
Step 3RBFNN.The phase space matrix constructed in Step 2 is used as the training set.Then the structure of the RBFNN is determined by RPCL,and its parameters is optimized by the k-means improved by IPSO and LM.The details of the network structure determination and parameter optimization are described in Subection 4.1 and Subection 4.2.Finally,a trained RBFNN is used to predict the target maneuver trajectory of the future moment.

Step 4Denormalization.By applying the maximum and minimum values saved in Step 1,the target maneuver trajectory predicted value returned by the RBFNN in Step 3 is denormalized,and then the actual target maneuver trajectory predicted value is obtained.

The flow chart corresponding to the above steps is shown in Fig.5.

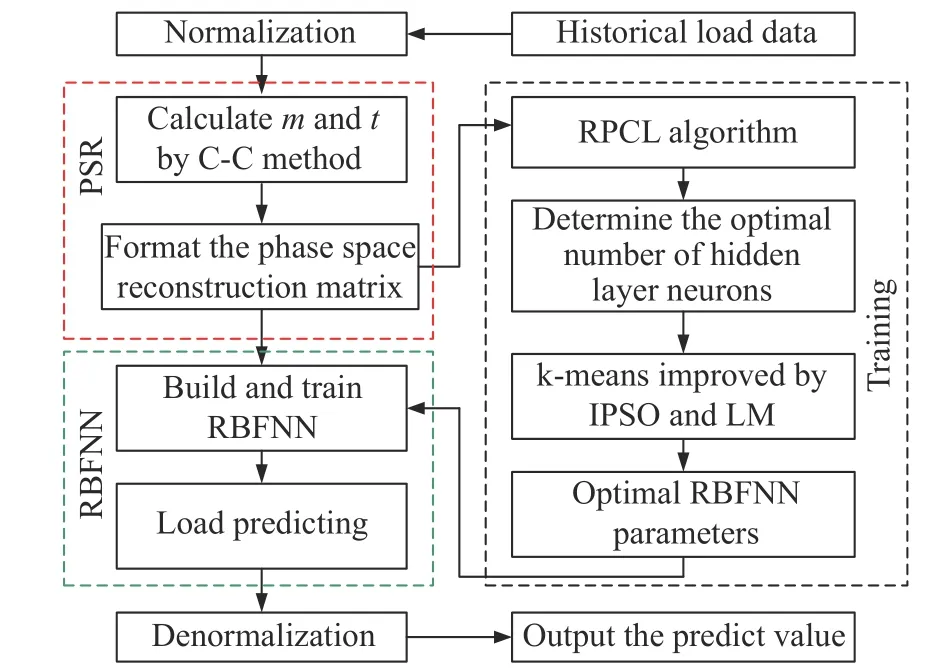
Fig.5 Flowchart of the PSR-RBF prediction model

5.Experiment result

5.1 Experiment setting

In order to verify the practical significance of the algorithm proposed in this paper,a period of air combat data is intercepted from air combat maneuvering instrumentation (ACMI),and 3 000 points are sampled continuously in a 0.1 s sampling period.The air combat trajectory is shown in Fig.6,and the sample data is shown in Fig.7.

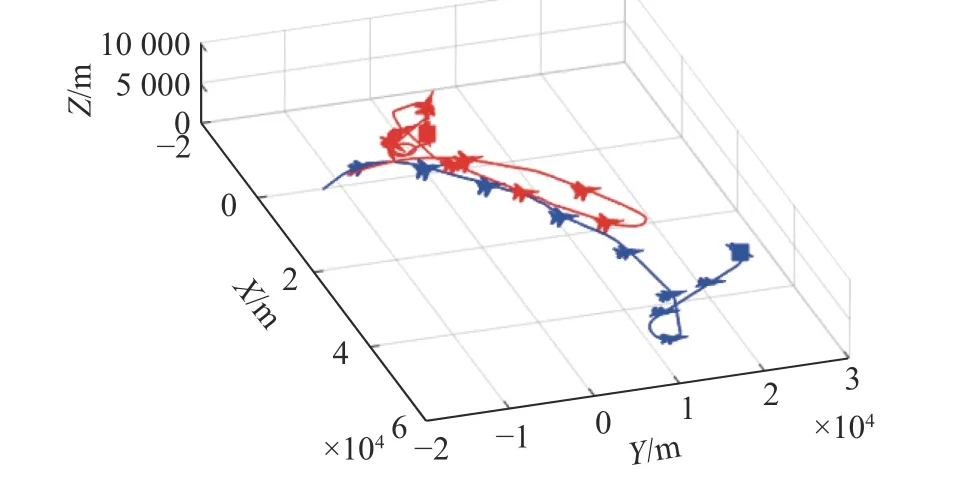
Fig.6 A complete air combat trajectory

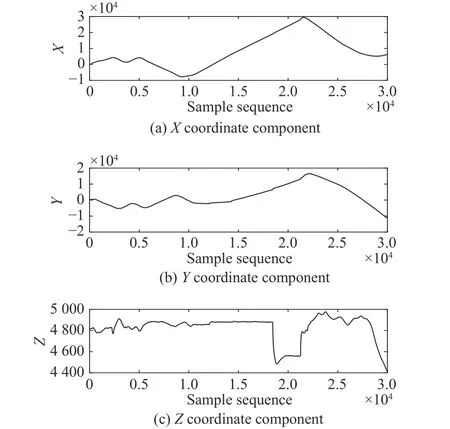
Fig.7 Sample data

In this paper,the software Matlab R2017a is used for simulation,and the CPU is Inter Core 3.00 GHz and 16 GB RAM.

5.2 Accuracy analysis

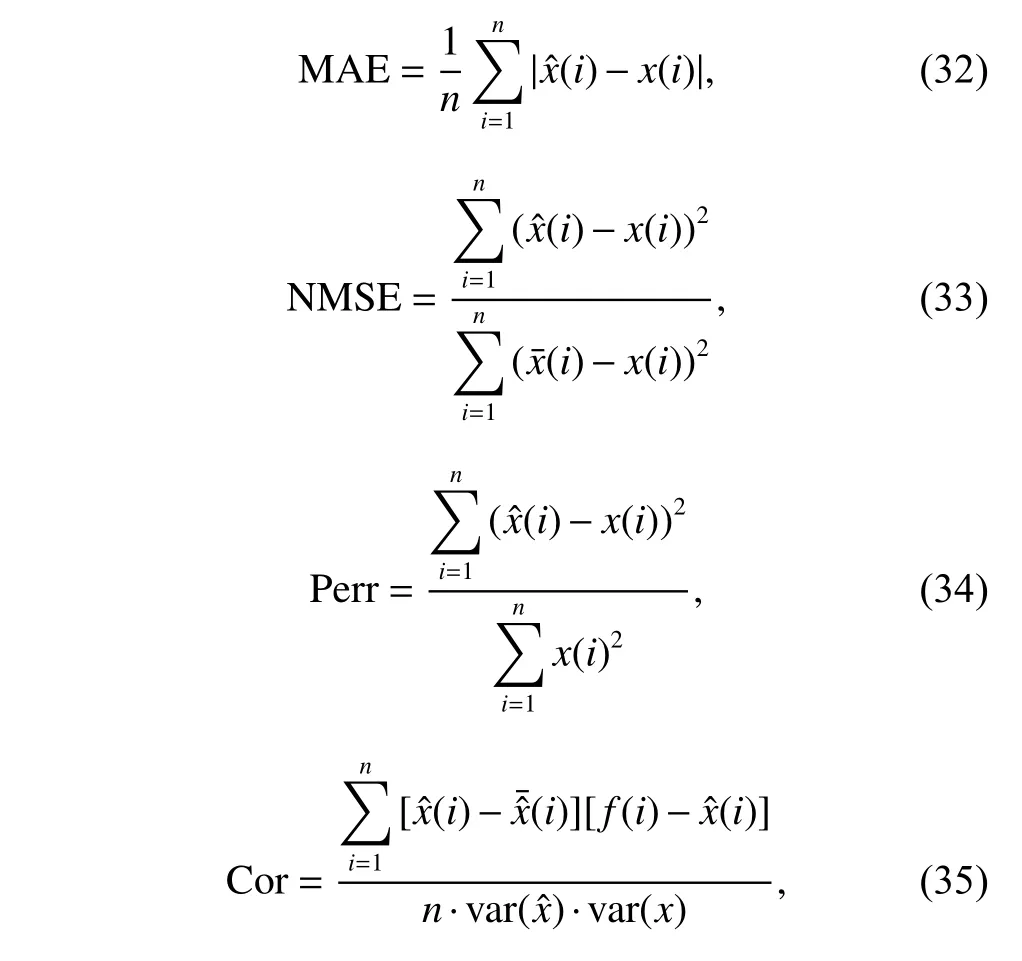
In order to compare the prediction results of different algorithms,the mean absolute error (MAE),mean square error (MSE),normalized mean square error (NMSE),relative error (Perr) and correlation coefficient (Cor) are used to evaluate the performance of the algorithms.The algorithm performance indicators are defined as follows:

In this paper,in order to compare the prediction effect of the traditional overall prediction method with the independent method mentioned,and to verify the advantages of the PSR-RBF prediction model,based on the above two prediction methods,the six neural network models including RBF[27],PSO-RBF[28],k-mensa-RBF[26],BP[12],kernel-based regularized least squares (KRLS)-RBF[29],and PSR-RBF are used to perform trajectory prediction.The differences of the independent method and the overall method are shown in Fig.8.Parameters of chosen algorithms are listed in detail as in Table 1.The traditional prediction method regards the three-dimensional coordinates as the whole as the input and output of the RBFNN.In this paper,the different nonlinear characteristics of three dimensions coordinates of the target maneuver trajectory are considered,so it is necessary to predict them separately to effectively improve the prediction performance.In this paper,the traditional prediction method regards the three dimensions coordinates as the whole,which is called the overall method,and the proposed method predicts three dimensions coordinates separately,which is called the independent method.

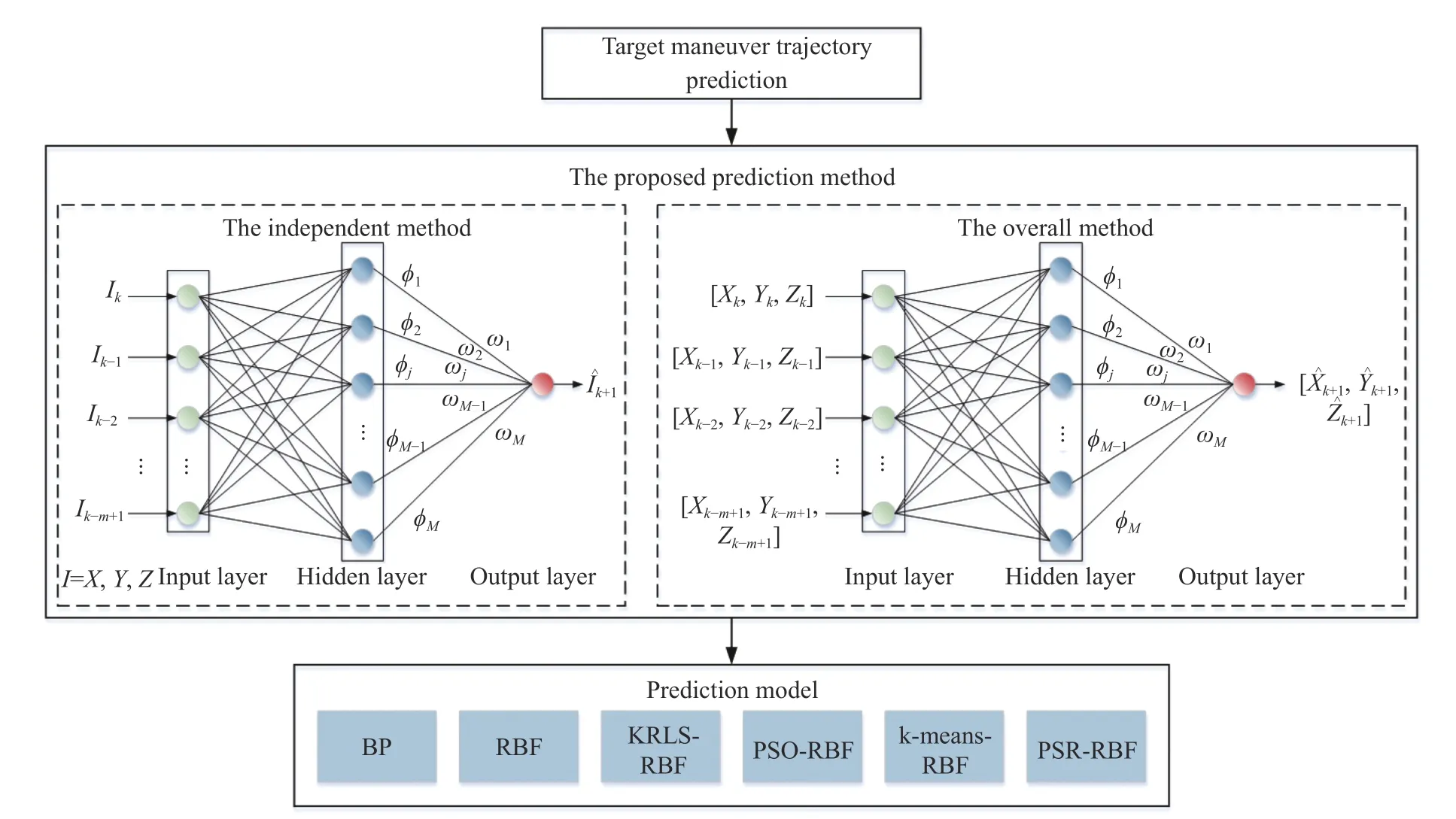
Fig.8 Differences of independent method and overall method

Table 1 Parameter settings for each algorithm

In this paper,the performance difference between the independent method and the overall method is compared and analyzed through simulation,and the prediction performance of six prediction models is also compared and analyzed.The simulation process is described in Subsection 5.2.1 and Subsection 5.2.2.

5.2.1 Experiment I:predictive performance comparison of the six models with independent method

The results of independent prediction of three-dimensional coordinates-based on six algorithms are shown in Fig.9−Fig.14,and the performance of the six algorithms is shown in Table 2.It can be clearly seen that the proposed model is more suitable than the compared models.The training values obtained by the developed model and other prediction models can well follow the changing trend of the actual values.

In addition,for Fig.9−Fig.14,except for the forecasting values obtained by PSO-RBF,the predicted values obtained by the other five prediction models can well follow the changing trend of the actual value.By comparing the prediction results shown in Fig.9−Fig.11,it can be seen that the prediction performance of RBFNN optimized by the IPSO and the k-means algorithm is better.

In terms of the mechanism analysis,the PSR-RBF model is proposed based on the PSR theory.The PSR can recover the attractor of the dynamic system in the highdimensional space,and the obtained information space can reflect the dynamic characteristics of the time series,and can better reflect the information contained in the time series,that is,the proposed model can better simulate the original system,so the prediction performance of the model is better than other algorithms.

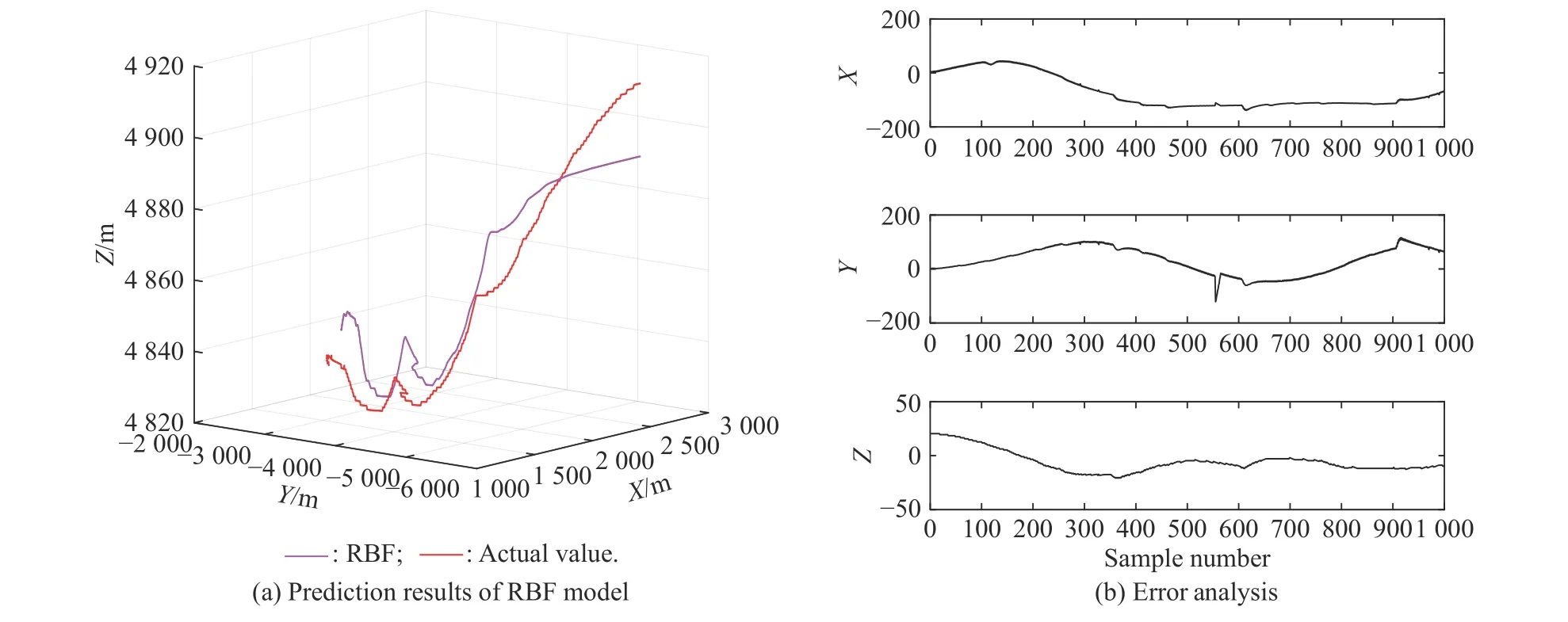
Fig.9 Comparison of prediction results of RBF model (Experiment I)

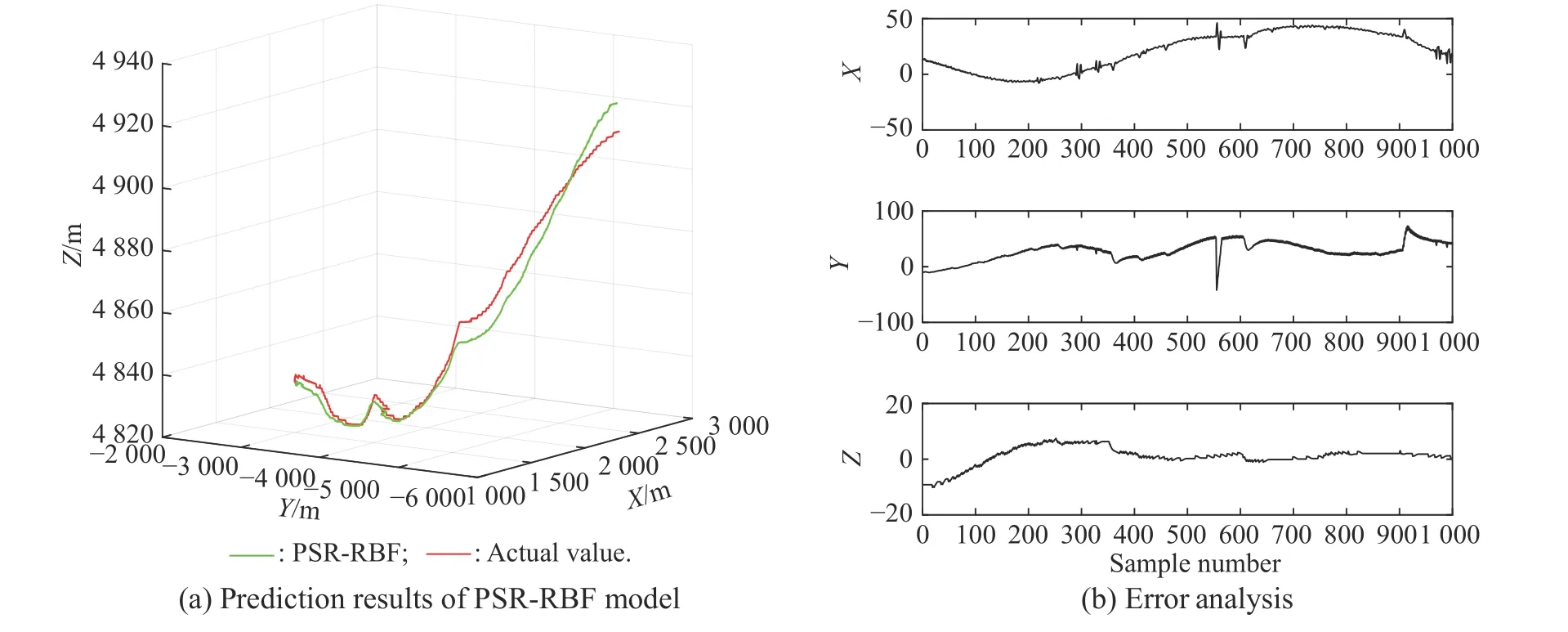
Fig.10 Comparison of prediction results of PSR-RBF model (Experiment I)

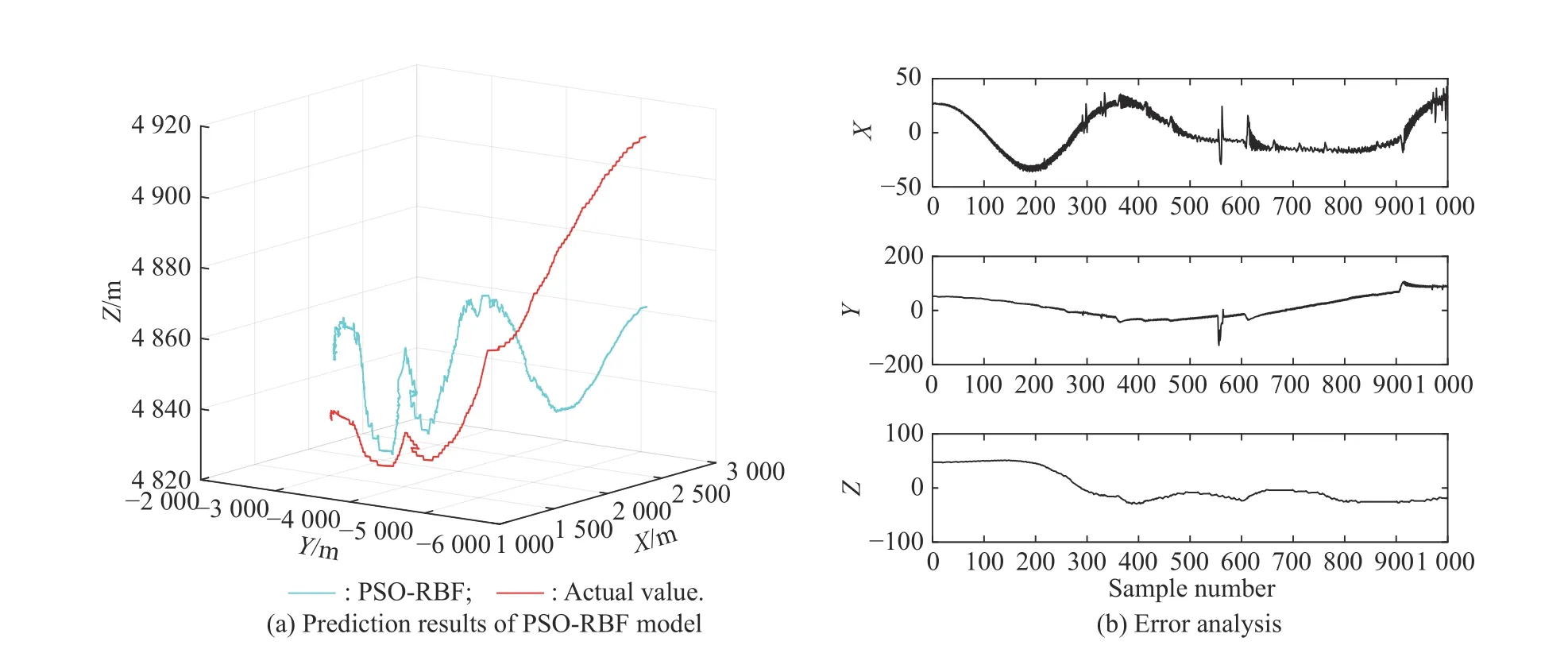
Fig.11 Comparison of prediction results of PSO-RBF model (Experiment I)

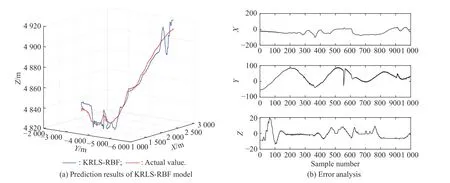
Fig.12 Comparison of prediction results of KRLS-RBF model (Experiment I)

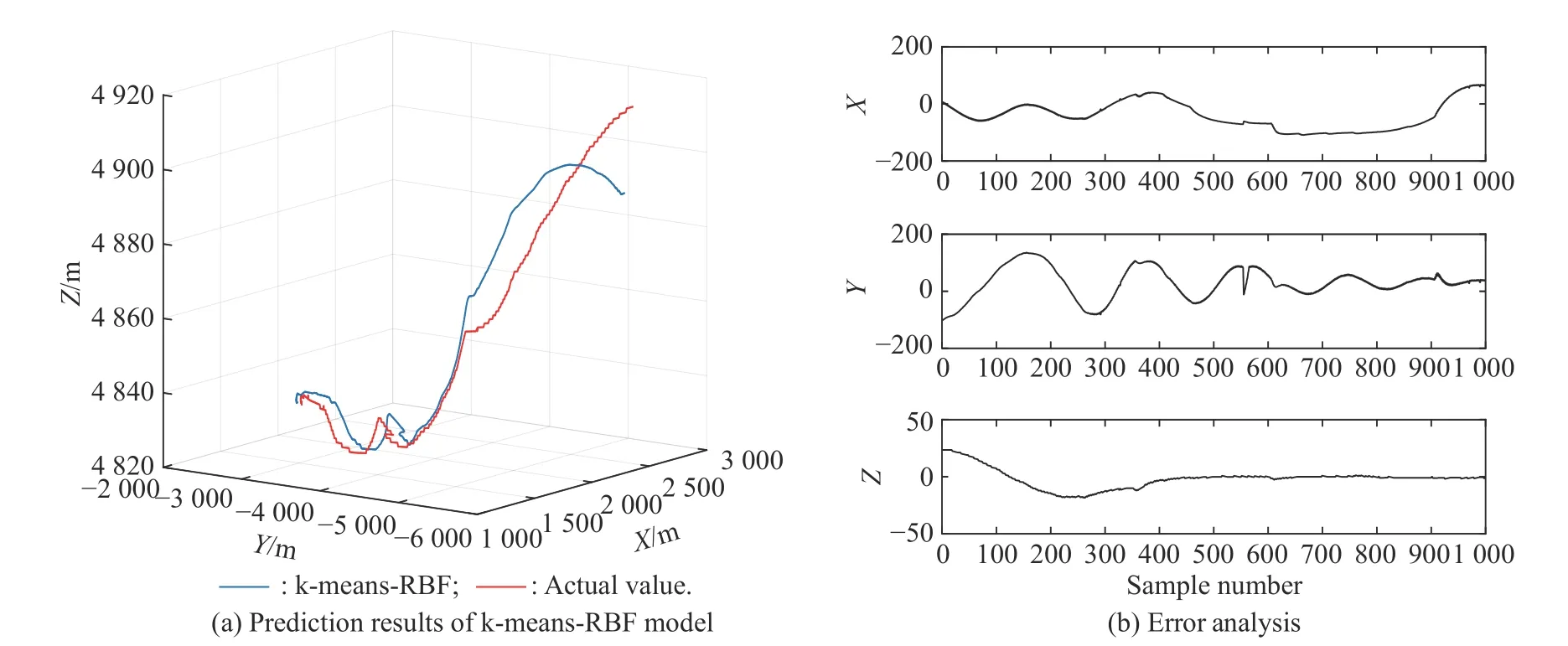
Fig.13 Comparison of prediction results of k-means-RBF model (Experiment I)

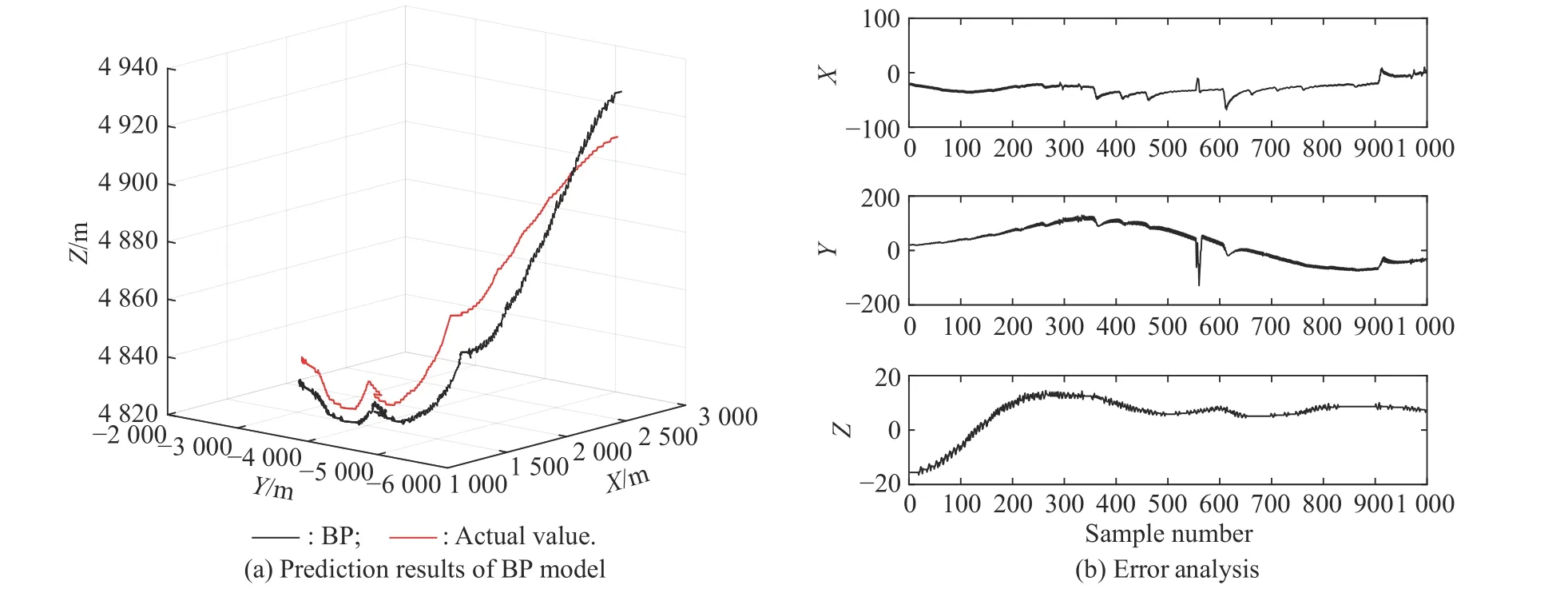
Fig.14 Comparison of prediction results of BP model (Experiment I)

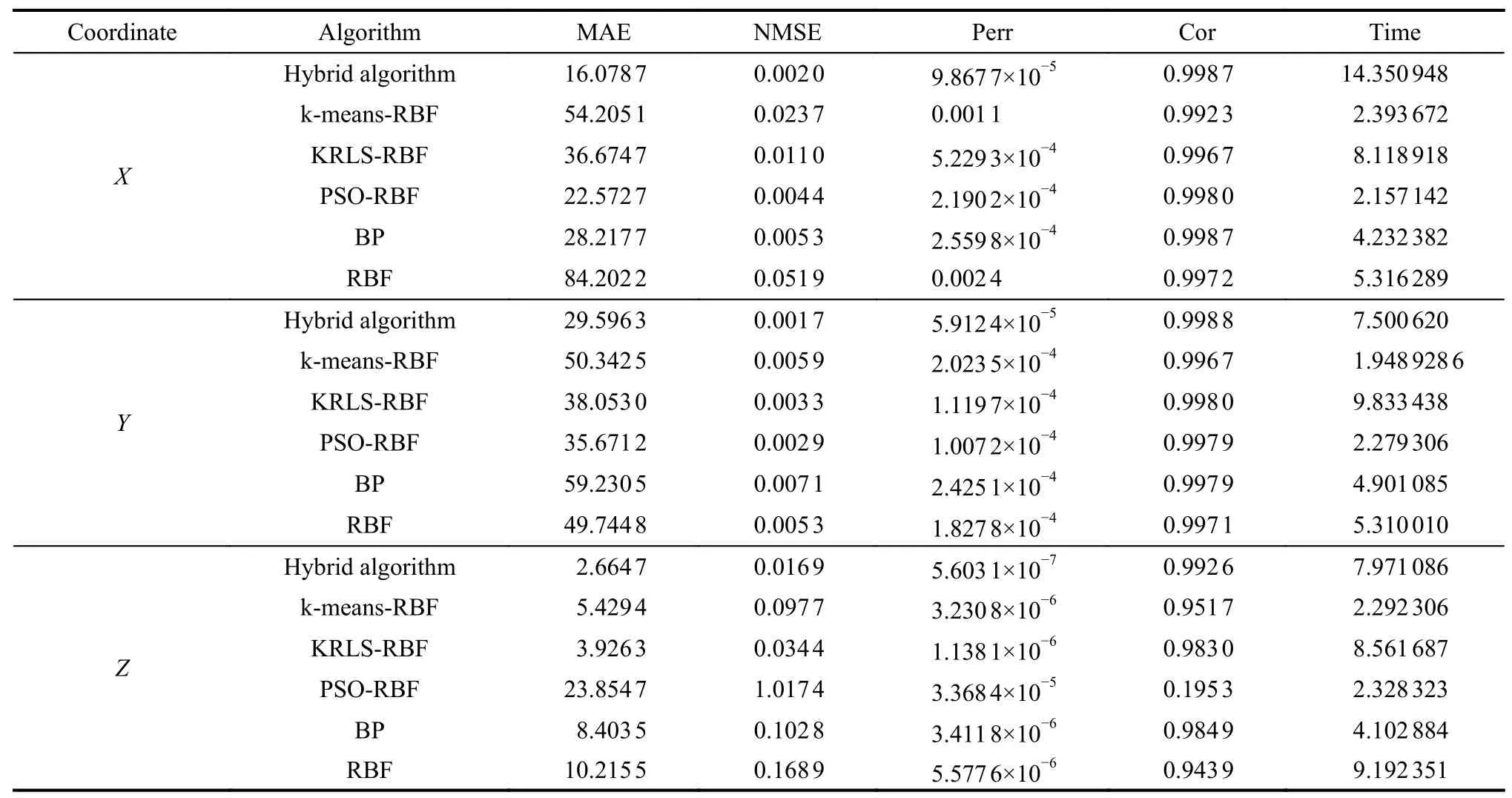
Table 2 Comparison of prediction performance of six models with independent method

5.2.2 Experiment II:predictive performance comparison of the six models with overall method

The results of overall prediction of three-dimensional coordinates based on six algorithms are shown in Fig.15−Fig.20,and the performance of the six algorithms is shown in Table 3,it can be clearly seen that except for the prediction errors of the PSR-RBF model,the prediction errors of the other five models are relatively large.This shows that the PSR-RBF model is also suitable for overall prediction.PSR can better reflect the information contained in the time series.Based on this information,RBF is used to extract the mapping rules contained in it,thereby improving the prediction performance of the model.By comparing the prediction results shown in Fig.15−Fig.17,it can be seen that the prediction performance of RBFNN optimized by the IPSO and the kmeans algorithm is better.The hybrid algorithm can better optimize the RBF parameters and improve the prediction performance of the PSR-RBF model.

By comparing the algorithm prediction results in Subsections 5.2.1 and 5.2.2,it can be seen that the prediction effect of the independent method is better than the overall method,and the prediction performance of the PSRRBF model is better than the other five prediction models.

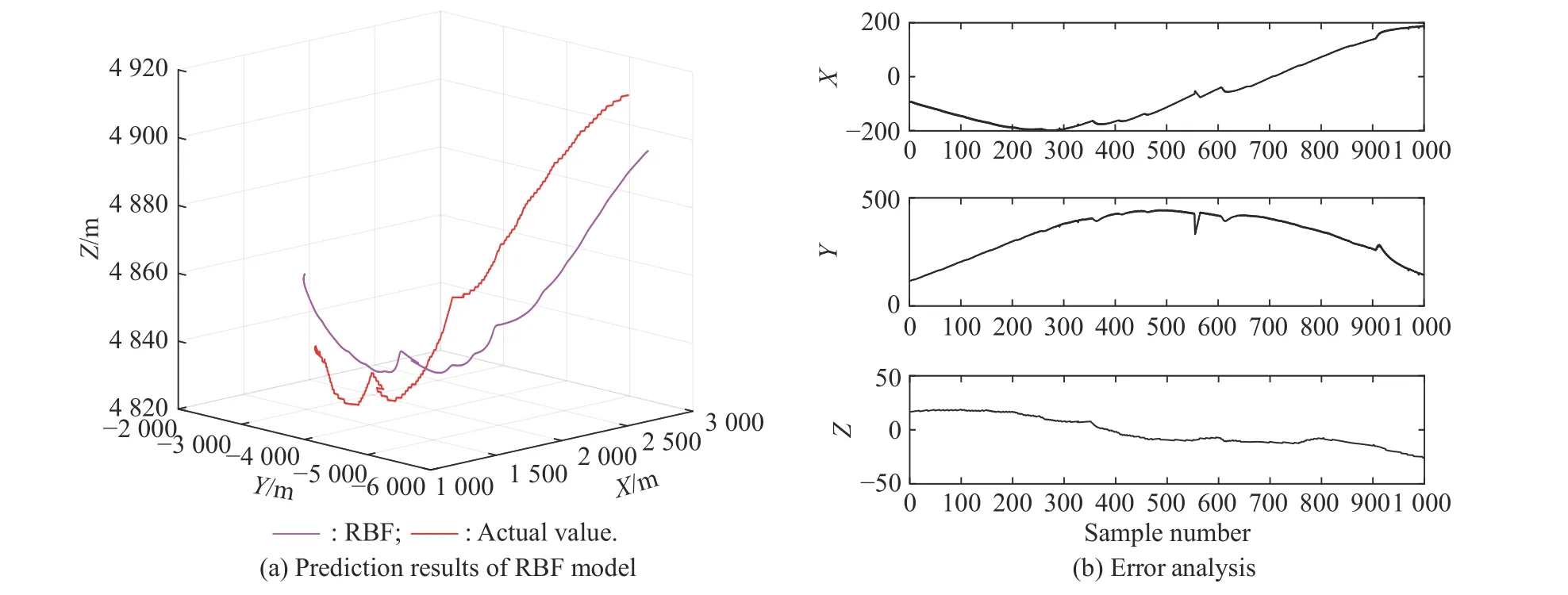
Fig.15 Comparison of prediction results of RBF model (Experiment II)

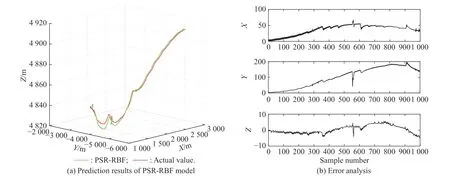
Fig.16 Comparison of prediction results of PSR-RBF model (Experiment II)

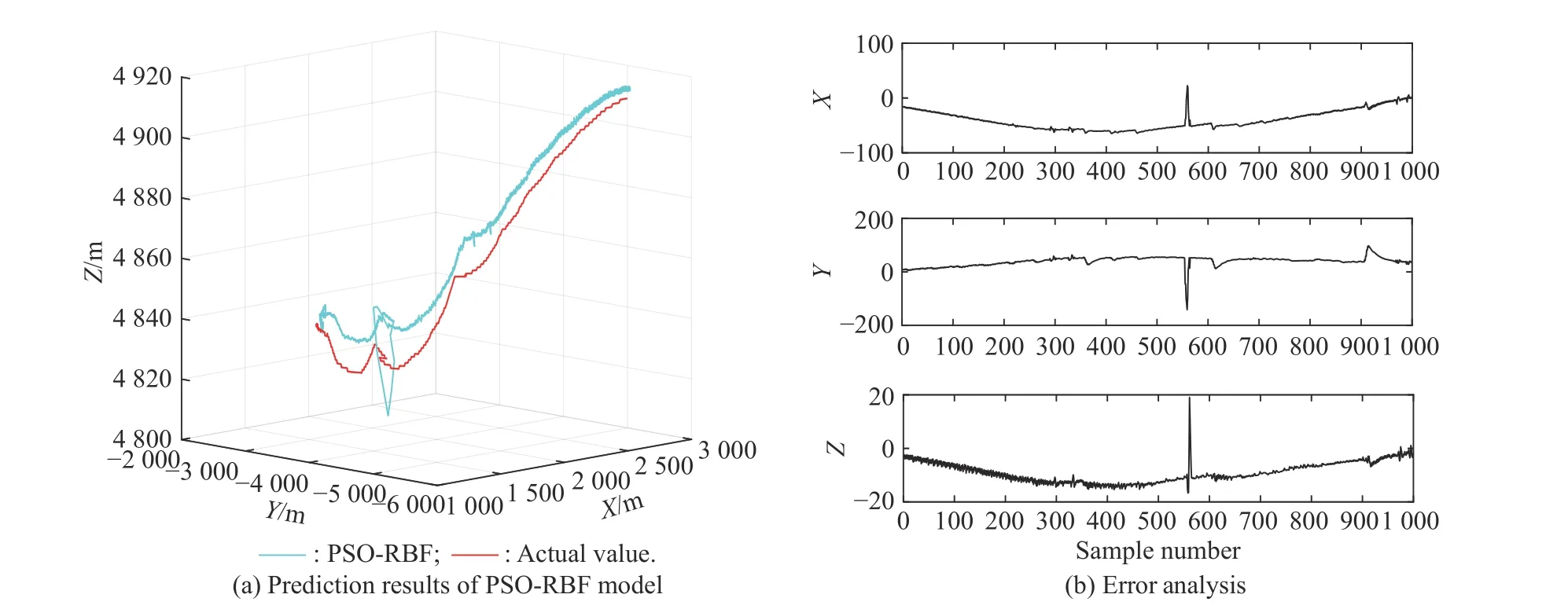
Fig.17 Comparison of prediction results of PSO-RBF model (Experiment II)

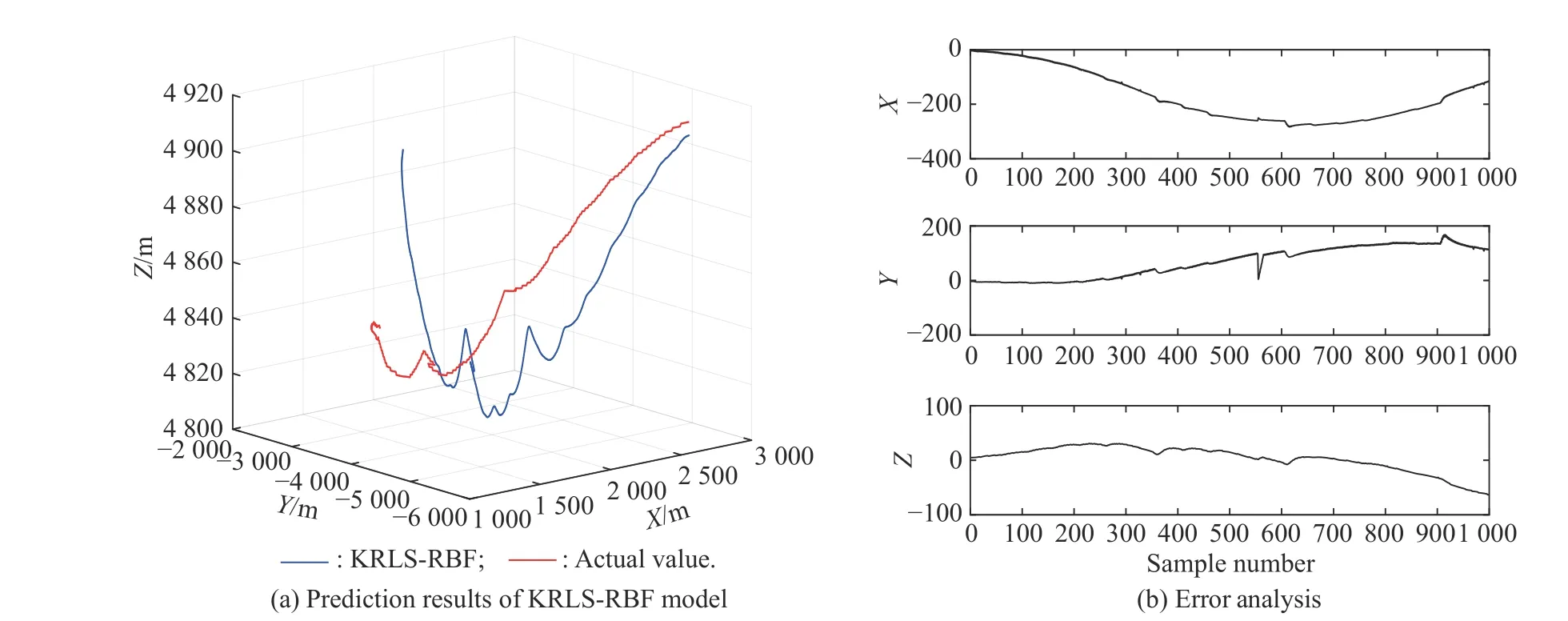
Fig.18 Comparison of prediction results of KRLS-RBF model (Experiment II)

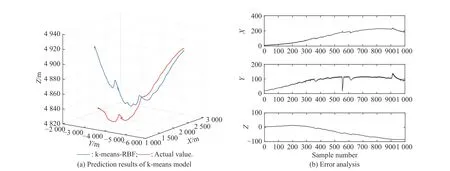
Fig.19 Comparison of prediction results of k-means-RBF model (Experiment II)

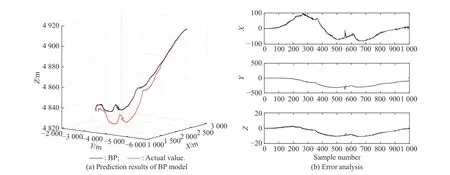
Fig.20 Comparison of prediction results of BP model (Experiment II)

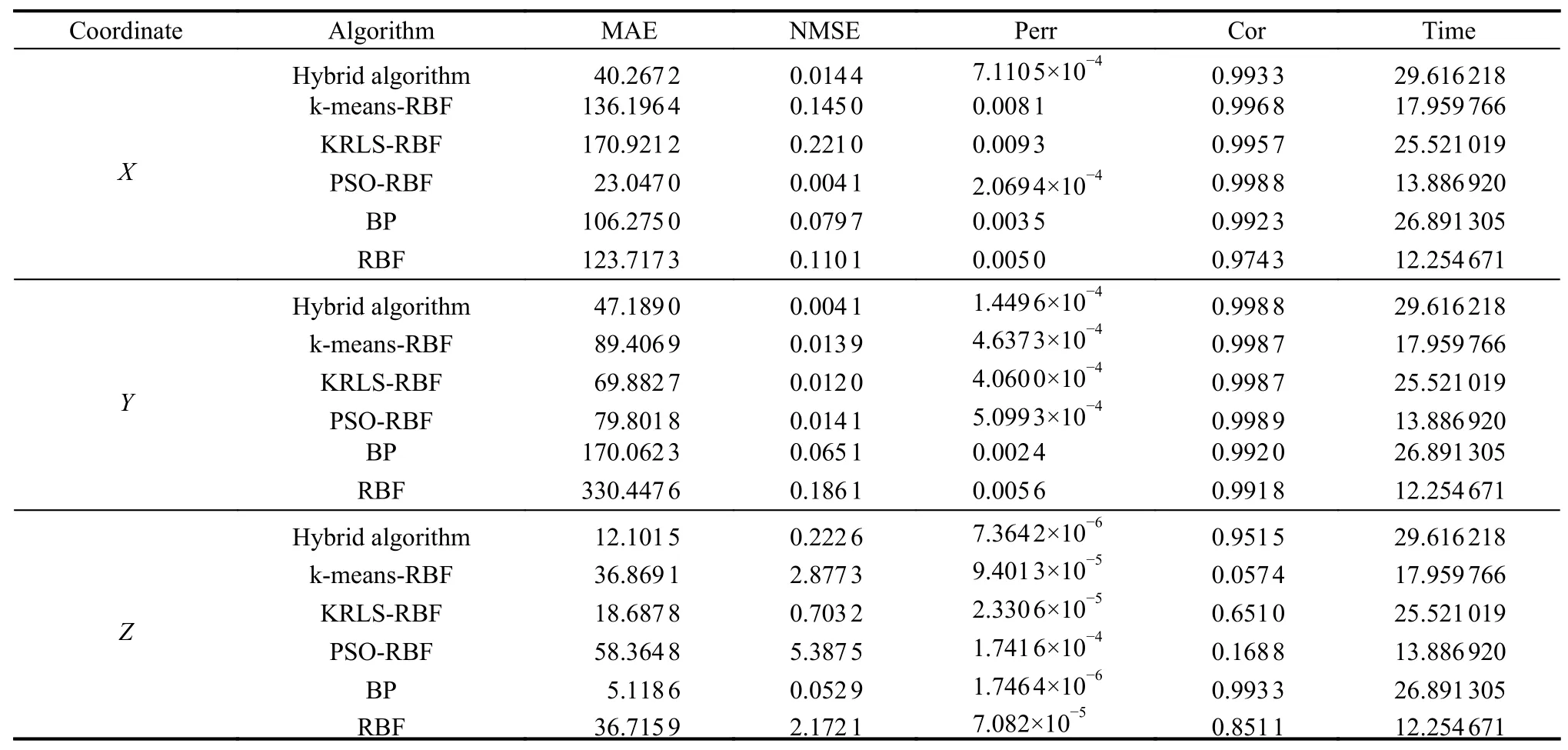
Table 3 Comparison of prediction performance of six models with overall method

At the method level,the whole method takes the three dimensions coordinates as a whole as the input and output of RBF,and ignores the characteristics of each coordinate.Based on the PSR theory,we can know that the optimal time delay and embedding dimension of the threedimensional coordinates are not the same,while the overall method sets the phase space reconstruction parameters of the three-dimensional coordinates to the same value,so that the information contained in each coordinate time series is not fully explored,resulting in poor prediction effect.At the model level,the structure and parameters of PSR-RBF are optimized by the hybrid algorithm,so that the optimized model is more suitable for the target maneuvering trajectory prediction,and the prediction performance is the best.

In this paper,the prediction performance of the proposed method is compared with that of the model.At the method level,the prediction performance of the independent method and the traditional whole method is compared and analyzed.The simulation results show that the prediction performance of each model using the independent method is better than that of the whole method.At the model level,the prediction performance of BP,RBF,PSO-RBF,KRLS-RBF and k-means-RBF models is compared and analyzed.The simulation results show that the PSR-RBF neural network prediction model based on proposed hybrid algorithm optimization is better than the overall method.The prediction performance of the model is better than the other five models,and has a good adaptability.The three-dimensional comparison results are shown in Fig.21 and Fig.22 where PSOK denotes PSO-k-means.

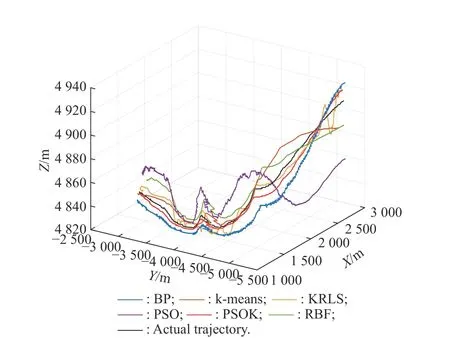
Fig.21 Comparison chart of trajectory by independent methods

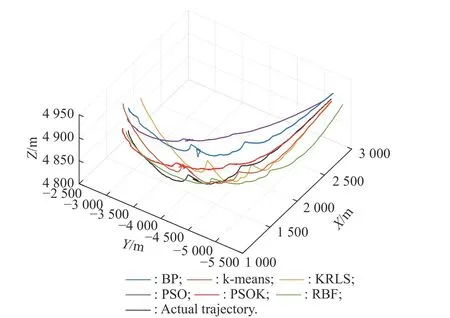
Fig.22 Comparison chart of trajectory by overall methods

5.3 Computional complexity analysis

According to the no free lunch (NFL) theorem [30],an algorithm cannot provide a better performance than all other algorithms in all aspects and problems,and each algorithm must comply with the conservation law.In the process of comparing the method and the model,the theorem is verified.In this paper,based on the independent method and the overall method,six models are used to predict the target maneuver trajectory,each model is tested 30 times,and the running time of each model is shown in Fig.23.As can be seen from Fig.23,for each model,the running time of the independent method is lower than that of the whole method;however,the running time of the model proposed is not the least.Combining the performance indicators of the algorithms in Table 2 and Table 3,it can be seen that the model proposed is not the optimal in terms of model running time,but other performance indicators are better than other models,so the NFL theory is verified.

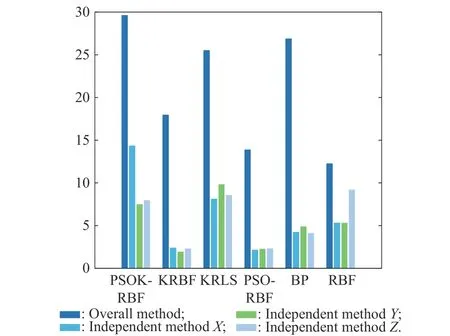
Fig.23 Comparison of the complexity of six algorithms based on the theory of two methods

6.Conclusions

In this paper,an independent prediction method and a PSR-RBF prediction model optimized by the hybrid algorithm are proposed.Based on the above method and the prediction model,the three-dimensional coordinates of the target maneuver trajectory are predicted independently,the three-dimensional coordinate time series are respectively projected by phase space reconstruction as the trajectory of a moving point in phase space,then the excellent non-linear fitting ability of the RBF network is applied to fit the trajectory,so as to realize target maneuver trajectory forecasting.The difficulty of applying RBF to target maneuver trajectory prediction is the determination of its structure and the optimization of related parameters,so the RPCL is used to determine the number of neurons in the hidden layer,the LM and the hybrid algorithm of IPSO and k-means are applied to optimize the parameter of RBF.There are also further improvements in the design of the RBF structure,one can try to use other algorithms to improve the neural network,or find other more suitable neural networks.

To solve the problem of target maneuver trajectory prediction,an independent prediction method is proposed,the three dimensions coordinates of the target maneuver trajectory are predicted separately by this method.At the same time,the prediction performance of the independent method is compared with the tradition method overall prediction method,the prediction result shows that the prediction performance of the proposed method is better.

The PSR-RBF forecasting model proposed is applicable to the prediction of target maneuver trajectory.Compared with other five RBFNN prediction models,the prediction accuracy of the PSR-RBF model is greatly improved.

In order to improve the prediction performance of the PSR-RBF model,RPCL is used to determine the structure of RBF,a hybrid algorithm of IPSO and k-means is applied to optimize the parameters of RBF.Compared with the PSO and k-means,the performance of the hybrid algorithm is better in optimizing RBF parameters.

In order to improve the authenticity and accuracy of the sample data,the actual air combat confrontation training data recorded by ACMI is used to construct training and test samples of the prediction model and method.This method effectively solves the problem of small and unreal sample data in the past.

In this paper,the accuracy of prediction methods and prediction models proposed is good.In practice,the way of sliding training and online use can be adopted.Within a certain time interval,a trained model is used first,and then the updated and trained new model is used for realtime prediction.This can save training costs and solve the shortcomings of completely offline training.