A dual population multi-operator genetic algorithm for flight deck operations scheduling problem
CUI Rongwei ,HAN Wei ,SU Xichao ,LIANG Hongyu ,and LI Zhengyang
1.Aeronautical Foundation College,Naval Aviation University,Yantai 264001,China;2.Aeronautical Operations College,Naval Aviation University,Yantai 264001,China;3.Unit 91404 of the PLA,Qinhuangdao 066000,China
Abstract: It is of great significance to carry out effective scheduling for the carrier-based aircraft flight deck operations.In this paper,the precedence constraints and resource constraints in flight deck operations are analyzed,then the model of the multi-aircraft integrated scheduling problem with transfer times(MAISPTT) is established.A dual population multi-operator genetic algorithm (DPMOGA) is proposed for solving the problem.In the algorithm,the dual population structure and random-key encoding modified by starting/ending time of operations are adopted,and multiple genetic operators are self-adaptively used to obtain better encodings.In order to conduct the mapping from encodings to feasible schedules,serial and parallel scheduling generation scheme-based decoding operators,each of which adopts different justified mechanisms in two separated populations,are introduced.The superiority of the DPMOGA is verified by simulation experiments.
Keywords:genetic algorithm,project scheduling,flight deck operation,transfer times of resources.
1.Introduction
The carrier battle group is an important symbol of national maritime comprehensive strength.As the core of the offensive and defensive system of the carrier battle group,the aircraft undertakes most of the combat mission.Its sortie rate is closely related to the ability to efficiently complete flight deck operations such as inspection,fueling,and oxygen filling.The purpose of the flight deck operations scheduling problem (FDOSP) is to shorten the makespan and efficiently complete all operations by reasonably arranging resources.Compared to the ground operations of aircraft on the airport,the carrier deck space is narrower,and the performing environment is more changeable,so operation and resource constraints of the aircraft carrier are more complicated [1].With the increasement in the sortie rate and the number of aircraft,higher requirements have been imposed on the flight deck operations scheduling capability,and the experience-based manual scheduling is inefficient in FDOSP [2].
In view of importance,complexity and the critical role in combat for FDOSP,it is of great significance to carry out effective scheduling for the aircraft fleet deck operations and resource allocation,establish a feasible scheduling model,and produce an efficient scheduling scheme[3].In recent years,FDOSP has become an emerging hot spot and many scholars have carried out a large number of studies on this issue.
This paper focuses on the scheduling of flight deck operations for the pre-flight preparation stage.On the basis of analysis of various constraints in the pre-flight preparation stage,the multi-aircraft integrated scheduling problem with transfer times (MAISPTT) is established,and the dual population multi-operator genetic algorithm(DPMOGA) is presented for the MAISPTT.The main contributions of this research are as follows:
(i) The precedence constraints,resource constraints,and transfer times of personnel and support equipment in the pre-flight preparation stage are described in detail.The MAISPTT is formulated as a mixed integer mathematical programming model with the objective of minimizing the makespan.
(ii) A scheduling optimization algorithm called DPMOGA is proposed.The dual population structure and random-key encoding modified by starting/ending time of operations are adopted.Various types of genetic operators are proposed,and the serial scheduling generation scheme (SSGS) or the parallel scheduling generation scheme (PSGS) are used to generate feasible schedules.An adaptive selection mechanism for genetic operators is designed.
The remainder of this paper is organized as follows.Section 2 presents a brief literature review of related work.Section 3 describes the MAISPTT.A mathematical programming model is presented in Section 4.In Section 5,the DPMOGA is proposed.Section 6 reports and discusses the results of the simulation.Finally,this paper is concluded by Section 7.
2.Literature review
2.1 Flight deck operations for pre-flight preparation stage
There are several variations of the scheduling model for pre-flight preparation according to different degrees of abstraction,which mainly include the hybrid flow-shop scheduling model [4],the flexible job-shop scheduling model [5],and the resource-constrained project scheduling problem (RCPSP) model [6−11].Researches based on the hybrid flow-shop scheduling model and the flexible job-shop scheduling model have disadvantages in meeting the complex networked constraints of operations,so most researches for FDOSP are based on RCPSP recently.In these researches,the support task of an aircraft is considered as a project,and the personnel and support equipment on the flight deck are considered as resources.Additionally,during the actual flight deck operations,it takes a certain amount of time to transfer personnel and support equipment from one work station to another,so the transfer times of personnel and support equipment between different work stations have to be considered.
2.2 Solving methods for RCPSPs
The RCPSP is an NP-hard combinatorial problem,and several methods for solving RCPSPs,including exact methods,heuristics and meta-heuristics,have been proposed.From the perspective of practicability and performance,the exact methods are computationally expensive for large-scale scheduling problems.Compared to exact methods,heuristics are easy to implement and computationally cheaper,but it is difficult to find an efficient priority rule that performs well for a broad range of RCPSPs [12].The meta-heuristics use intelligent optimization algorithms to find better encoding,then generate a feasible schedule using schedule generation schemes(SGS),which provide the best trade-off between practicability and performance,and have attracted the attention of researchers and provided improvements for solving RCPSPs.Several meta-heuristics,including the differential evolution algorithm [12],improved particle swarm optimization (IPSO) [13],and the hybrid estimation of distribution algorithm (HEDA) [14],were proposed for solving the RCPSPs.As a classic evolutionary algorithm,the genetic algorithm (GA) has been widely used for RCPSPs [15−19].To the best of our knowledge,GA has not been applied to the pre-flight preparation operations scheduling problem with resource transfer times.And how to effectively select each genetic operator to improve the search ability and convergence speed for specific problems remains to be studied.
3.Description of MAISPTT
3.1 Description of flight deck operations
The launching and landing cycle of the aircraft fleet is a multi-stage task.After the deck operations are completed,the aircraft will taxi to the designated catapult to complete launching according to the sortie plan.After completing the combat mission in the air,the aircraft finally completes the recovery mission and return to the aircraft carrier.If it is necessary to dispatch these aircraft again,they will repeat the above process [10].Pre-flight preparation,which is the main stage of flight deck operations of FDOSP,has complicated precedence and resource constraints.After aircraft landing on the flight deck,a tractor will tow it from the temporal parking spot to the service parking spot for pre-flight preparation.Once chocked and chained,the aircraft will turn to the preflight preparation stage,during which inspections,alignment of inertial navigation system (INS),fueling,oxygen filling and nitrogen charging,are completed by different professional personnel.Support equipment mainly provides various types of supply resources such as fuel,ammunition,oxygen and nitrogen [20].
The launching and landing cycle of the aircraft is proceeded in a deck cycle way,which means an aircraft fleet will go through pre-flight preparation,launching and landing on the flight deck within a deck cycle.To avoid the disorder and ensure the sustainability of cyclic operations,the duration of each deck cycle is regulated,including the modes of 1+00 (1 h 0 min),1+15 (1 h 15 min),etc.Any delay of pre-flight preparation may disturb the operating tempos under such a time-critical scheduling[11].The goal of MAISPTT is to minimize the makespan and increase sortie rates.
3.2 Constraints of MAISPTT
Constraints of MAISPTT consist of precedence constraints and resource constraints.Specifically,resource constraints can be divided into personnel constraints,support equipment constraints,work station space constraints,and supply resource constraints.
(i) Precedence constraints
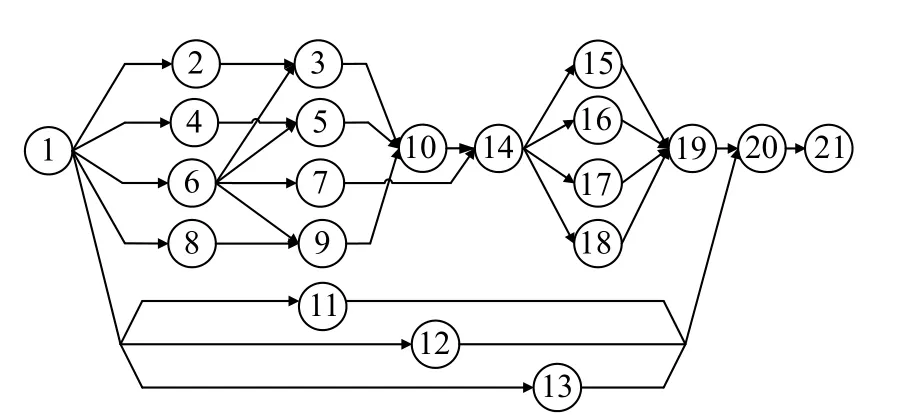
For a given sortie mission,an aircraft fleet (denoted as a setI={1,2,···,|I|}) is designated to perform the flight deck operations before launching.The operations of each aircrafti∈Iis denoted asJi={1,2,···,|Ji|},containing a dummy starting operation,a dummy ending operation,and |Ji|−2 real operations.All operations of fleet are denoted asJ={(i,j)|i∈I,j∈Ji}.Referring to the RCPSP,the support task of a single aircraft can be regarded as a project,and the precedence constraints of the aircraft fleet can be described by the activity on node (AoN) network as shown in Fig.1,where an operation is represented by a node,and the precedence constraints between activities are denoted by the arcs.
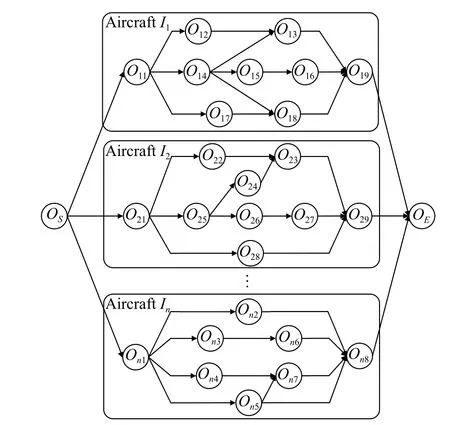
Fig.1 AoN network for aircraft fleet
In Fig.1,Oi jdenotes thejth operation of theith aircraft,OSandOEare the dummy starting operation and the dummy ending operation respectively.The operationOij,whose work station space isWij,cannot be performed earlier than operations in its immediate predecessors set Ψij.The starting time and ending time of operationOijare denoted asSijandEi jrespectively,andEi j=Si j+di j,wheredi jis the duration ofOij.Aitdenotes the set of operations of aircraftiwhich are active in periodt.Moreover,aircrafticannot start its operations until it has been chocked and chained in the service parking spotpiat the released timeExi.
(ii) Personnel constraints
Kpdenotes the set of personnel trade types,Lpkdenotes the set of personnel with tradek(k∈Kp),Lpk={1,2,···,|Lpk|},rpijkdenotes the number of personnel with tradek(k∈Kp) required for performing operationOij.The transfer time of personnel with tradek(k∈Kp)between operationOegand operationOijis denoted aswhereDWi j,Wegdenotes the distance between work station spaceWijandWeg,vpkdenotes the transfer velocity of personnel with tradek(k∈Kp).
(iii) Support equipment constraints
There are two kinds of support equipment,i.e.,sharing equipmentKesand exclusive equipmentKeu.Kedenotes the set of support equipment trade types,Ke=Kes∪Keu,Lekdenotes the set of support equipment of the typek(k∈Ke),Lek={1,2,···,|Lek|} .denotes thelth support equipment of the typek(k∈Ke)which can reach thepth parking spot,otherwise,Equipment can only support the aircraft which are within the range of their pipelines.reijkdenotes the number of support equipment of the typek(k∈Ke) required for performing operationOij,reijk∈{0,1}.The transfer time of the support equipment of the typekbetween operationOegand operationOijis denoted aswhich consists of setup time of the support equipment of the typek(denoted asuk),and moving time of the support equipment from work station spaceWijtoWeg(denoted aswherevekdenotes the transfer velocity of equipment).The setup time is considered both before and after performing operation,soFig.2 shows a sketch map of personnel and equipment transfer process on flight deck of the Admiral Kuznetsov aircraft carrier.
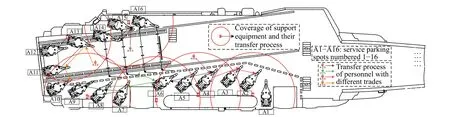
Fig.2 Resources on flight deck of the Admiral Kuznetsov aircraft carrier
(iv) Work station space constraints
These constraints are considered only for the work station with limited space (e.g.,cockpit) for personnel.Ksdenotes the set of work station space types,andnsikdenotes the maximum number of personnel who are perf orming concurrently in thekth (k∈Ks) type work station space of theith aircraft.Setrsi jk=1 if operationOijis performed in work station space of the typek(k∈Ks),otherwise,rsi jk=0.
(v) Supply resource constraints
Kwdenotes the set of supply resource types.Lwkdenotes the maximum number of aircraft that the supply resource of typek(k∈Kw) can support at the same time,and setrwijk=1 if the supply resource of typek(k∈Kw)i s required while performingOij,otherwise,rwijk=0.
4.Mathematical formulation of MAISPTT
4.1 Problem assumptions
(i) Each operation cannot be interrupted during its execution.
(ii) The duration of each operation is deterministic.
(iii) All kinds of resources are available for each service parking spot.
4.2 Decision variables
BesidesSij,Eij,∀(i,j)∈J,the other relevant decision variables used in the model are as follows:

4.3 Mathematical expression of MAISPTT
MAISPTT is formulated as a mixed integer mathematical programming model:
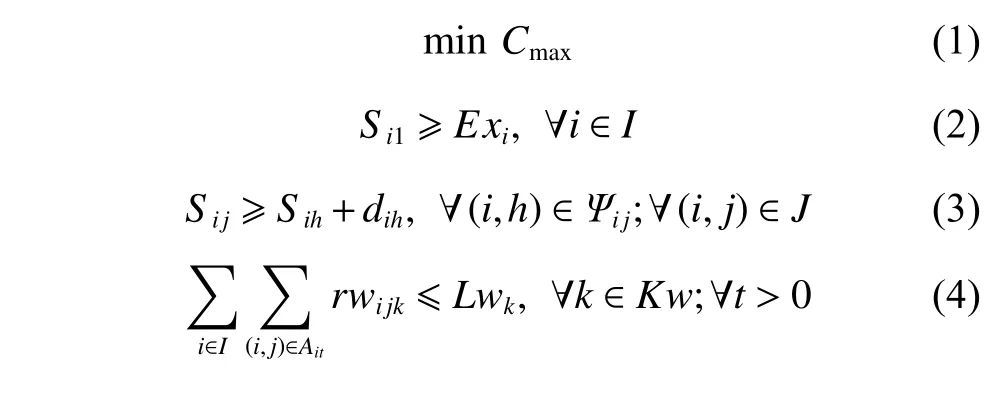

Formula (1) represents that the objective is to minimize the makespanCmaxof the aircraft fleet.Constraint (2)indicates that aircrafticannot start its operations until it is chocked and chained in the service parking spot at the released timeExi.Constraint (3) denotes the precedence constraints of operations.Oijcannot be performed earlier than its immediate predecessors.Constraint (4) states that the total number of aircraft on the flight deck that are supported by supply resource of the typek(k∈Kw) concurrently at the time periodtis smaller than the maximum numberLwk.Constraint (5) indicates that the number of personnel who are performing concurrently in thekth(k∈Ks) type work station space of theith aircraft at the time periodtis smaller than the maximum numbernsik.Constraint (6) denotes that equipment can only support the aircraft which are within the range of their pipelines.Constraint (7) represents that if operationOijprecedes operationOegand they are allocated to the same personnellwith tradek(k∈Kp),the operationOegcannot be performed until this personnel transfers to work station spaceWegafter completing operationOij,whereBMis a large enough positive number.Constraint (8) is related to the transfer time sequence relationship between two adjacent operations,which are allocated to the same exclusive support equipment,or the same sharing support equipment while these two operations do not belong to the same aircraft.The transfer time sequence is similar to that in constraint (7).Constraint (9) indicates that if more than one operation of aircraftirequire a sharing equipment of the typek(k∈Kes) at any time period,these operations are allocated to the same one.Constraints (10) and (11) together make sure that the number of personnel or equipment required for performing operationOijis equal to the total number of personnel or equipment allocated to it respectively.Constraints (12) and (13) express relationships between decision variables.Constraint (14) indicates the values of decision variables.
5.The proposed DPMOGA
MAISPTT is a large-scale combinatorial optimization problem where precedence constraints and four renewable resources constraints need to be premeditated.In this paper,MAISPTT is considered as a resource-constrained multiproject scheduling problem with transfer times,and it is an NP-hard optimization problem.Hartmann et al.[21]pointed out that the most successful approaches for RCPSPs were meta-heuristics,one of which was GA.In this section,we describe DPMOGA to solve MAISPTT.
The flowchart of the DPMOGA is shown in Fig.3.
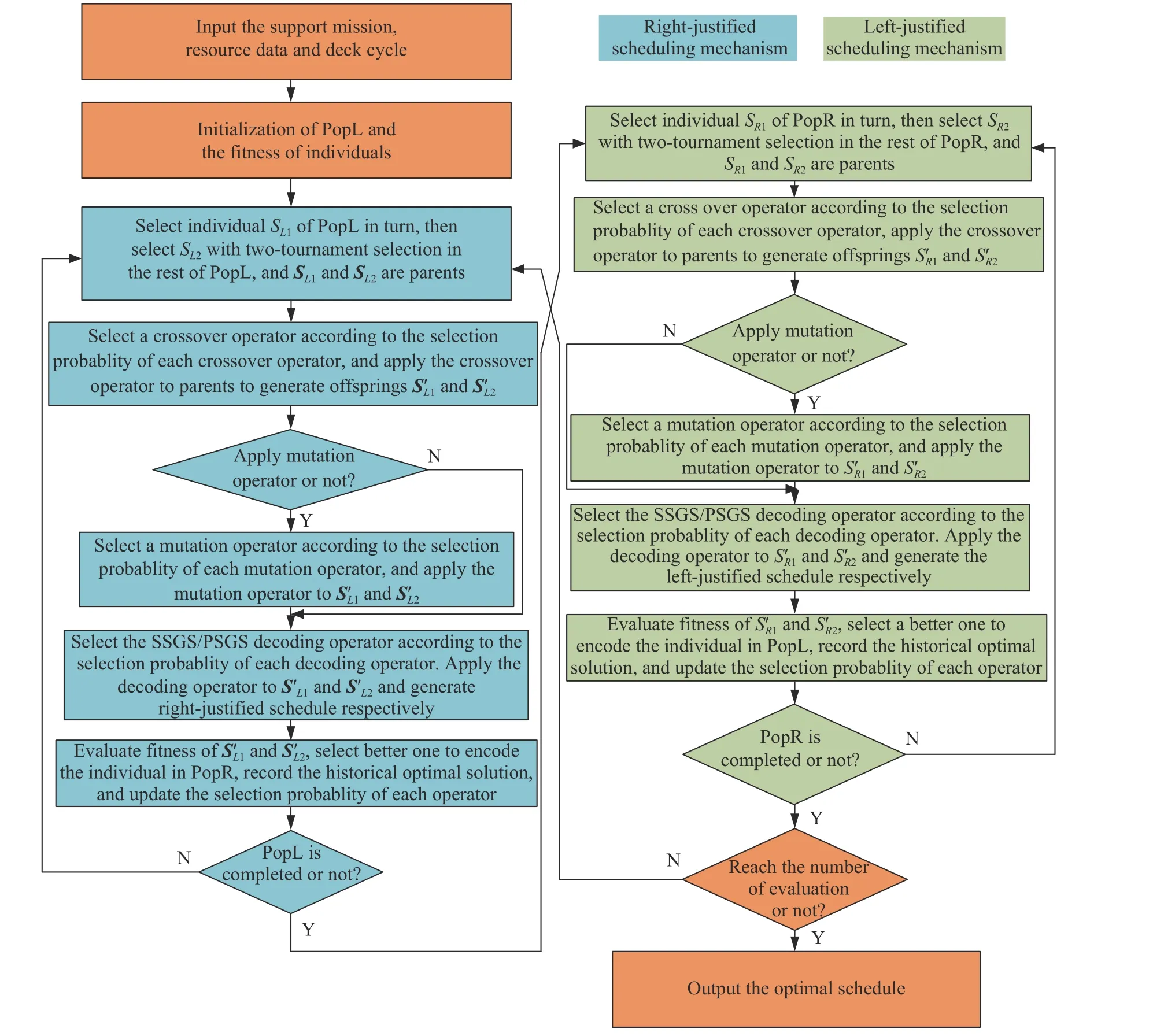
Fig.3 Flowchart of DPMOGA
A left population PopL and a right population PopR are involved in our algorithm.In PopL,a right-justified scheduling mechanism is adopted to generate the right-justified schedule and the starting time of each operation in the schedule is used to encode the individual in PopL,while in PopR,a left-justified scheduling mechanism is adopted to generate the left-justified schedule and the ending time of each operation in the schedule is used to encode the individual in PopL.
Various types of genetic operators are proposed in our algorithm.In addition,an adaptive operator selection mechanism is set to choose the best performing genetic operator according to the performance of operators at each iteration.The fitness of individualSis denoted asfS,which can be represented by theCmaxof the generated schedule,and a lowerCmaxindicates a better fitness.
Compared with the GA,the DPMOGA is mainly improved in the following aspects.
(i) The dual population structure [18]is adopted,and the evolution process of population is divided into the leftjustified scheduling mechanism and the right-justified scheduling mechanism.The double justification (DJ)technology is applied to all individuals in the population to enhance the algorithm’s performance.
(ii) The encodings of individuals are modified by the starting/ending time of operations,which promises that one schedule can be represented by one encoding.Additionally,encodings are adjusted between the starting and the ending time of the operations of the scheduling plan,which increases the diversity of population.
(iii) Different genetic operators behave differently during the execution of the algorithm,and the best performing genetic operator will be selected by the adaptive operators selection mechanism for the evolution of the population.This method increases the stability and the probability of the DPMOGA.
5.1 Solutions encoding
Kolisch and Hartmann [22]distinguished five different schedule encodings,but the activity-list (AL) encoding and the random-key (RK) encoding are the most widespread.Debels et al.[23]indicated that the RK leads to promising results due to the use of the topological ordering (TO) notation.In our algorithm,the RK encoding modified by the starting/ending time of operations is adopted.Compared with AL and RK,our encoding promises that one schedule can be represented by one encoding.Set the encoding of individualSaswhereRKijindicates the priority of operationOij.
(i) For PopL,after generating the right-justified schedule,we encode the individualSRin PopR using the starting time of each operation in the schedule,i.e.,SR=
(ii) For PopR,after generating the left-justified schedule,we encode the individualSLin PopL using the ending time of each operation in the schedule,i.e.,SL=
5.2 Crossover operators
We adopt four kinds of crossover operators,which are described with taking PopL as an example.
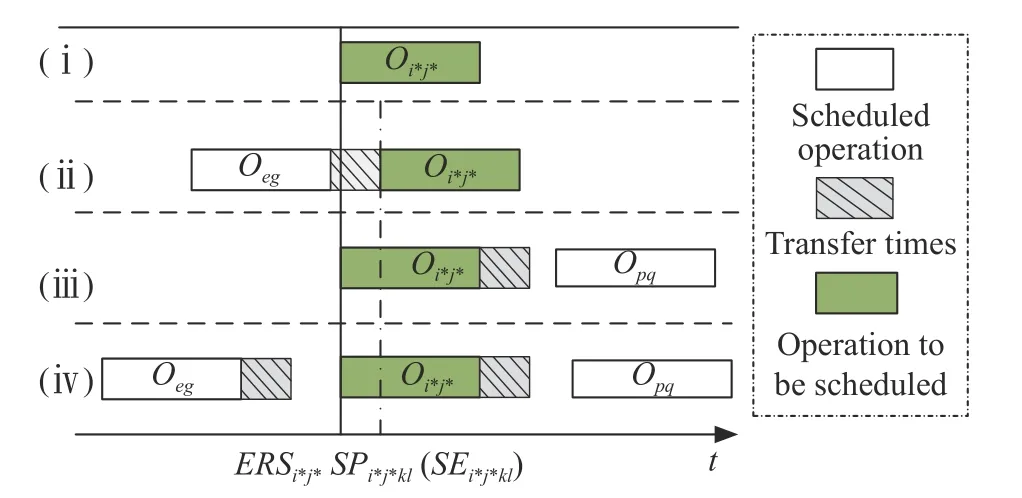
Crossover 1:One-point crossover operator.An integerposis generated randomly,where 1 Crossover 2:Two-point crossover operator.Integerpos1 andpos2 are generated randomly,where 1 Crossover 3:Arithmetic crossover operator.When this crossover operator is applied to parentsSL1andSL2,the offspringsare calculated as whereaandbare random numbers,a,b∈[−0.5,1.5],a+b=1.The values ofaandbare not limited to [0,1],which ensures that the search area of the arithmetic crossover operator covers the parents’ neighborhood more widely. Crossover 4:Direction-based heuristic crossover operator.The origin version of this operator was proposed by Wang et al.[24],who indicated that there is a great chance to produce better offsprings to improve the convergence speed of the algorithm.DenoteC=SL2−SL1,r1iandr2i(i=1,2,···,J) are random numbers limited to[0,1],C1=[r1i ci]1×J,C2=[r2i ci]1×J,step λ=1,the offspringsare calculated as 5.3.1 Adaptive mutation probability Our adaptive mutation probabilityPmis based on mean fitness variance: whereNPis the population size,andDrepresents the maximum deviation between the fitness of individuals in the population and the average fitness,Pmis calculated as wherekis a random number limited to [0.3,0.6],andis a threshold value.Pm0is a relatively small initializing mutation probability.When the individual difference in the population decreases,the mean fitness variance of the population decreases accordingly.At this time,increasing the individual mutation probability has an advantage of helping the algorithm jumping over the local optimal solution.In addition,a random numberrandis generated in each cycle,rand∈[0,1],ifrand 5.3.2 Mutation operators We adopt four kinds of mutation operators in our algorithm. Mutation 1:One-point mutation operator.An encoding is selected randomly and then modified to (rand−0.5)·RKmax,whereRKmaxis the maximum of encodings. Mutation 2:One-operation mutation operator.An operationOijwith the latest ending timet1of its predecessors and the earliest starting timet2of its successors in the schedule,is selected randomly.The encoding of operationOijis modified to a random number limited tot1+dij,t2(for individual in PopL) or a random number limited tot1,t2−dij(for individual in PopR). Mutation 3:Multi-operation of one aircraft mutation operator.Na(Na∈Z[|Ji|/3,|Ji|×2/3]) operations of a single aircraftiare selected randomly,then each encoding of them is modified by the method in Mutation 2. Mutation 4:Project reorganization mutation operator.Aircrafti(i∈I) is selected randomly and the encodings of all the operations of this aircraft are initialized according to precedence constraints. Decoding is a key stage to conduct the mapping of individual encoding to schedule and evaluate the fitness by using SGS.The most widespread SGS in RCPSPs is SSGS or PSGS [25].In our algorithm,the SSGS-based decoding operator and the PSGS-based decoding operator are proposed simultaneously.For PopL,the right-justified SSGS-based or right-justified PSGS-based decoding operator is applied to generate the right-justified schedule,while for PopR,the left-justified SSGS-based or the the left-justified PSGS-based decoding operator is applied to generate the left-justified schedule.The related notations are described in Table 1. Table 1 Related notations in decoding operators 5.4.1 Left-justified SSGS-based decoding scheme There are |J| stages totally in SSGS.Cgis initialized with the dummy starting operation of each aircraft,and the starting time of operations inCgare set as the released time of corresponding aircraft.At each stageg,the set of eligible operations is calculated,from which the operation to be scheduledwith the highest priority (minimal RK) is chosen. Then the earliest precedence-resource-feasible starting time of operationis initialized by the earliest precedence-feasible starting time of it.To arrange the operation which satisfies the constraints of personnel,support equipment,work station space and supply resource in the duration,the timeis postponed until the earliest resource-feasible starting time of the four kinds of resource is equal,i.e.,Afterwards,the starting timeis determined as the earliest precedence-resource-feasible time.In order to allocate personnel and support equipment for the operation after determiningthe personnel allocation rule and the support equipment allocation rule simultaneously are proposed as follows. Rule 1:Personnel allocation rule based on the minimum accumulated transfer distance first (MATDF).If the operation to be scheduled requires personnel with tradek(k∈Kp),the accumulated transfer distanceTTklof each personnellwith tradekthat can support the operation is calculated,then personnel are allocated for the operation with the ascending order ofTTkl. Rule 2:Support equipment allocation rule based on the minimum total performing time remaining in the cover area (MTRCA).If the operation to be scheduled requires support equipment of the typek(k∈Ke),the total performing time remaining in the cover area of each support equipmentlof the typekthat can support the operationTRklis calculated as follows: where the set of remaini ng operations is At the end of this loop,all the state parameters and the set of scheduled operations are updated for the next stage.The pseudo code of the left-justified SSGS-based decoding scheme is shown in Algorithm 1,Algorithm 2 and Algorithm 3. Algorithm 1Algorithm of the left-justified SSGSbased decoding scheme Fig.4 Scheduling timeline of personnel or support equipment The difference for scheduling timeline between personnel and support equipment is transfer times in Fig.4.The procedure to judge whether personnellcan perform operationOijand to calculateis described as follows,and the procedure to judge support equipment and to calculateis similar. 5.4.2 Left-justified PSGS-based decoding scheme The pseudo code of the left-justified PSGS-based decoding scheme is shown in Algorithm 4.In this operator,there are |J| stages at most.At the beginning,wheng=1,the setsAgandCgare initialized with the dummy starting operation of each aircraft and null set respectively,and the starting time of operations inAgare set as the released time of corresponding aircraft.Then at each stageg,if all the processors of an operation are scheduled,the operation can be added into setDg.tgis calculated as the earliest ending time of operations in setAg−1.All operations inDgare arranged in the ascending order ofRKij.For each operationOi∗j∗∈Dg,if required resources are feasible at periodtg,its starting timeSi∗j∗is set as the earliest time when all required personnel and support equipment are transferred to work stationWi∗j∗.Sinceit is necessary to determine whether any other personnel or support equipment can perform operationOi∗j∗at periodSi∗j∗.The personnel allocation rule and support equipment allocation rule are also Rule 1 and Rule 2 simultaneously. Algorithm 4Algorithm of the left-justified PSGSbased decoding scheme 5.4.3 Right-justified SSGS/PSGS-based decoding scheme Operations can also be scheduled oppositely by the rightjustified scheduling mechanism,that is,all operations are shifted to the right except for the first and last operations,and the schedule starts from the final operation’s immediate predecessors.In this way,the ending time is set as late as possible. Contrary to the left-justified scheduling mechanism,the operationOijis added toCg,if and only if all the successors ofOijare scheduled.Cgis initialized with the dummy ending operation of each aircraft,and the ending time of operations inCgare set late enough to ensure that all operations start from a positive time.A larger RK indicates a higher priority in the right-justified scheduling mechanism.The personnel allocation rule and the support equipment allocation rule are also Rule 1 and Rule 2.Then after the right-justified scheduling planis generated,the makespan can be reduced by subtracting a span ∆TLfrom the whole schedule,where(Si1−Exi),and the final right-justified scheduling plan is o btained asSij,Eij=Si j,Eij−∆TL. This section describes how to select a genetic operator.Our selection mechanism is based on the mechanism in the consolidated optimization algorithm (COA) proposed by Elsayed et al.[12].Nfdenotes the type number of genetic operators,for crossover operators and mutation operators,Nf=4,for decoding operators,Nf=2.Let’s take the crossover operators as an example.In theCSth cycle,the improvement rate of theith crossover operator is denoted asIm(CS,i)(i=1,2,···,N f).InitializeIm(1,i)=0(i=1,2,···,N f) at the beginning of the algorithm,once theith crossover operator is applied to the individualSin theCSth cycle,Im(CS,i) is updated as whereCmax,oldis the minimalCmaxin the last cycle.The improvement rate is updated in PopL or PopR respectively.Moreover,ifIm(CS,i)0,it is initialized to a small enough positive numberSM=10−5.It is worth noting that there is a mutation probability before applying a mutation operator.If no mutation operator applies to the individual,the improvement rate will not update.The selection probability of theith crossover operator in the next cycle is calculated as Also,in the case that no improvement in the fitness after a crossover operator is applied to the individual,all the selection probabilities of each crossover operator in the next cycle are set to be equal. The crossover operators,the mutation operators,and the decoding operators are key parts of the DPMOGA.The complexity of crossover and mutation operators is shown in Table 2.The computational complexity of DPMOGA is mainly reflected in decoding operators.According to[26],the complexity of SSGS and PSGS is bothO(|J|2R),whereRis the number of renewable resource types.In the MAISPTT,the decoding operation of PopL and PopR is consistent.The status of four resources have to be considered while finding feasible resources,and the complexities for finding personnel,support equipment,supply resources,and work station space areand Table 2 Complexity of genetic operators The simulation cases are generated based on the Admiral Kuznetsov flight deck as shown in Fig.2.The general AoN network is shown in Fig.5.There are 19 real operations to be performed for each single aircraft except for the dummy starting operation (numbered 1) and the dummy ending operation (numbered 21).The numbers regarding the types of personnel,support equipment and supply resources are |Kp|=4,|Ke|=7,and |Kw|=5 respectively,and the required unit of personnel and support equipment for all the relevant operations is 1.Only one kind of work station space (cockpit) is considered,i.e.,|Ks|=1,and the maximum number of personnel who are performing concurrently in cockpit is 1.In addition,the maximum number of aircraft that each supply resource can support at the same time is set as [Lw1,Lw2,···,Lw5]=[9,14,2,4,6]. Fig.5 AoN network of single-aircraft According to [10],the configured number of personnel should be determined based on mission and experience.PSdenotes the average personnel strength,and the number of personnel with tradek(k∈Kp) is calculated as In our simulation experiments,the deck cycle is set as The first five types support equipment (numbered 1−5)are fixed stations,and their configured numbers are[|Le1|,|Le2|,···,|Le5|]=[7,16,6,6,8].Among these fixed stations,support equipment No.2 is sharing support equipment,while others are exclusive support equipment.Moreover,support equipment No.6 and No.7 are mobile equipment,which can be regarded as stationary equipment whose support coverage is the whole area of flight deck,and their configured number is sufficient and without constraints. The personnel transfer velocity is set asvpk=5 km/h,∀k∈Kp.For support equipment numbered 1−6,their transfer velocity is set as 3 km/h,and the setup time is set as [u1,u2,···,u6]=[20,10,30,30,20,20].The distance matrix between work stations,the requirements and duration of each operation are large-scale and not listed. Three types of mission cases are described in Table 3.There are two average personnel strengths,PS=1.8 andPS=3.2 in each mission case. Table 3 Mission cases There are three key parameters needed to be discussed in the proposed DPMOGA,i.e.,the population sizeNPin each population,the threshold valuein adaptive mutation probability,and the initializing mutation probabilityThe Taguchi method of design of experiment (DOE)[27,28]is used to determine a set of suitable parameters for the DPMOGA in this section.Combinations of different values of these parameters are shown in Table 4.Experimental evaluation among three mission cases withPS=1.8 is conducted.We run the DPMOGA 20 times independently for each mission case with the maximum number of evaluationQ=10 000.The average response variable (ARV) values are the following average deviation values: whereCijis thejth makespan of theith mission case obtained by the DPMOGA,LBiis the lowest makespan of theith mission case obtained by the DPMOGA. Table 4 Combinations of parameter values The average ARV of each level for parameters is shown in Table 5,where Delta is the range of average ARV for each parameter,and Rank is the significance rank of each parameter. According to Table 5,it can be seen thatNPis the most significant parameter among the three parameters.The best combination of parameter values areNP=60, Table 5 Average ARV of orthogonal experiments To evaluate the performance of the proposed DPMOGA,experiments comparison among different mission cases is conducted.Four different algorithms for RCPSPs,i.e.,the efficient genetic algorithm (EGA) [17],IPSO [13],the multi-modal genetic algorithm (MMGA) [16],and HEDA[14],are used to make a comparison with DPMOGA.All settings for the compared algorithms are using the same settings proposed in the previous studies. After 20 independent runs for each algorithm with the maximum number of evaluationQ=10000,the results are shown in Table 6.The performance of each algorithm is measured by the average makespan (Avg.),the best makespan (Best.),and the variance of 20 results of each algorithm (Var.).Furthermore,according to [29−32],the minLTF priority rule or the minSLK priority rule performs better while solving the RCPSP,so comparisons with priority rules are also conducted.The evolutionary convergence curves of the five algorithms for three missions with twoPSlevels are shown in Fig.6.In Table 6,for all cases andPSlevels,the average makespan and the best makespan obtained by DPMOGA are better than that obtained by other algorithms,and except Mission 2 withPS=1.8,the variance of results obtained by DPMOGA is also better than that obtained by other algorithms.From the prospective of average makespan in all the mission cases withPS=1.8,we can see that as the number of aircraft increases,the difference between the average makespan obtained by DPMOGA and that obtained by other algorithms is increasing.The heuristics using PSGS with the minLTF priority rule and the minSLK priority rule perform poorly,but the calculation speed is fast.Also,the value ofPShas a strong impact on the makespan.WhenPSis larger,the configured number of personnel in each mission case increases,so the best and the average makespans obtained decrease obviously. Table 6 Results of experiments As for the four compared algorithms,their performance is different in different cases.For EGA,it outperforms the other three compared algorithms from the perspective of the average makespan in Table 6.The variance of results obtained by EGA is relatively small,and especially in all the mission cases withPS=1.8,EGA gets the smallest variance in the four compared algorithms.The best makespan obtained by EGA is usually better than that obtained by MMGA and HEDA.In the EGA,another two genes are added into the AL encodings in order to select the SGS and justification direction.Similar to our DPMOGA,this algorithm can adaptively select a better performing SGS and justification direction during the iteration process to generate a scheduling plan.For IPSO,the best makespan obtained is better than that obtained by other three compared algorithms in most mission cases.However,it can be seen in Table 6 that the variance obtained by IPSO is the largest.Also,this algorithm no longer converges after a certain number of iterations as shown in Fig.6.These phenomena show that the IPSO has poor stability and is easy to fall into the local optimal solution.For HEDA,this algorithm performs moderately but better than MMGA in most mission cases from the perspective of three performance measurements.For MMGA,it usually performs the worst in the four compared algorithms,whether from the perspective of the average makespan or the perspective of the best makespan.We can also find that the convergence speed of the MMGA is slower from Fig.6.However,MMGA obtains the lowest best makespan in Mission 3 withPS=3.2.Another phenomenon (also appears on HEDA) is that,when the value ofPSdecreases,the variance of results obtained by MMGA becomes larger.As thePSvalue decreases,the number of personnel decreases,and the optimization space becomes smaller,so it is difficult for MMGA to find a better solution within a limited number of iterations. Fig.6 Evolutionary convergence curves for mission cases The EGA performs better than the other three compared algorithms.In order to show the improvement of the DPMOGA,the Kruskal-Wallis test for the results obtained by DPMOGA and EGA is carried out.We propose the null hypothesis H0:results obtained by DPMOGA and EGA come from the same sample.The result of the hypothesis test is shown in Table 7.We can see that thepvalues under different test conditions are all extremely small.Therefore,we have sufficient certainty to reject the null hypothesis. Table 7 Results of the Kruskal-Wallis test In this paper,the scheduling problem of flight deck operations for the pre-flight preparation stage is studied.The MAISPTT is considered as a resource-constrained multiproject scheduling problem with transfer times.In view of the NP-hard nature of MAISPTT,the DPMOGA is proposed.In the simulation section,the best combination of parameter values are determined by the Taguchi method.To evaluate the performance of the proposed DPMOGA,simulation experiments among different mission cases with different personnel strengths are conducted.Simulation experiment results show that the DPMOGA outperforms some other state-of-the-art algorithms. In the future,three main tasks require more in-depth research.Firstly,as we can see in Section 6,the value ofPShas a strong impact on the makespan.This inspires us to analyze the impact of resource composition,and then study the joint optimization method for scheduling and resource configuration.Secondly,more efficient optimization algorithms for FDOSP need to be studied.Thirdly,many uncertain factors may influence the operation scheduling,so the dynamic scheduling method and the robust scheduling method also need to be considered.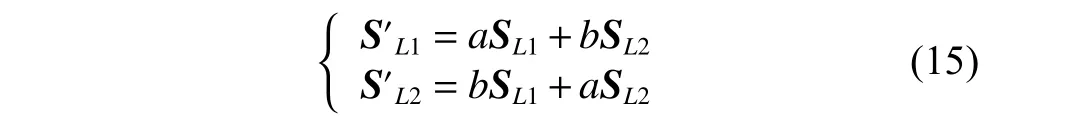
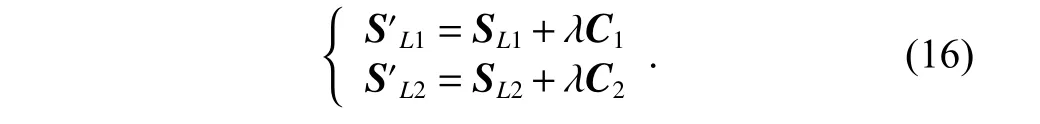
5.3 Adaptive mutation probability and mutation operators
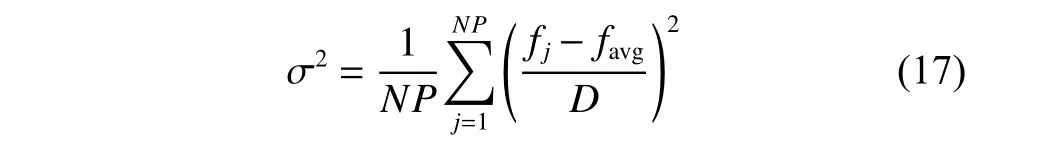
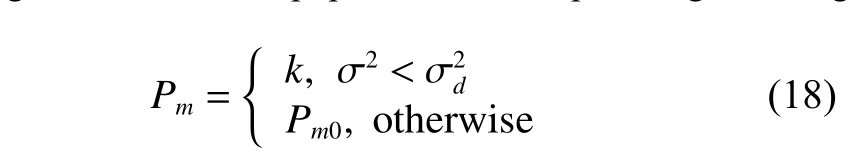
5.4 Decoding operators

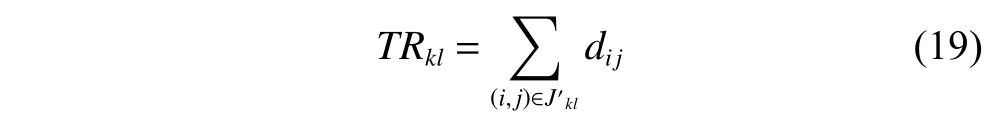







5.5 Adaptive operators selection mechanism
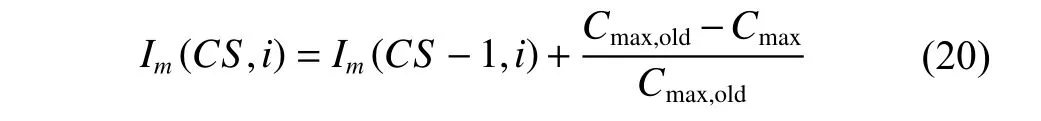
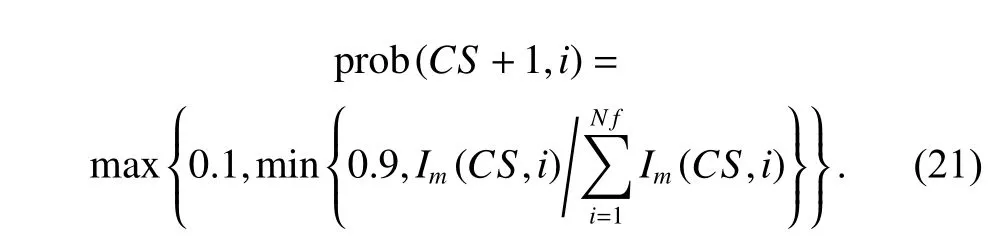
5.6 Computational complexity analysis

6.Simulation experiments
6.1 Mission cases generation
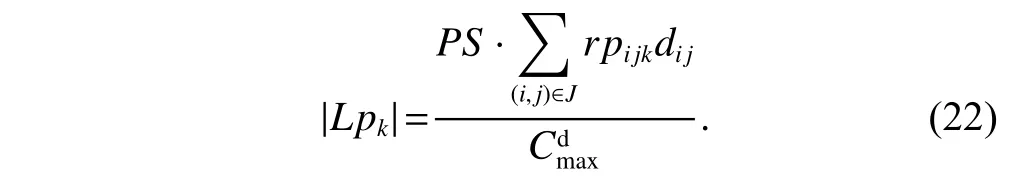

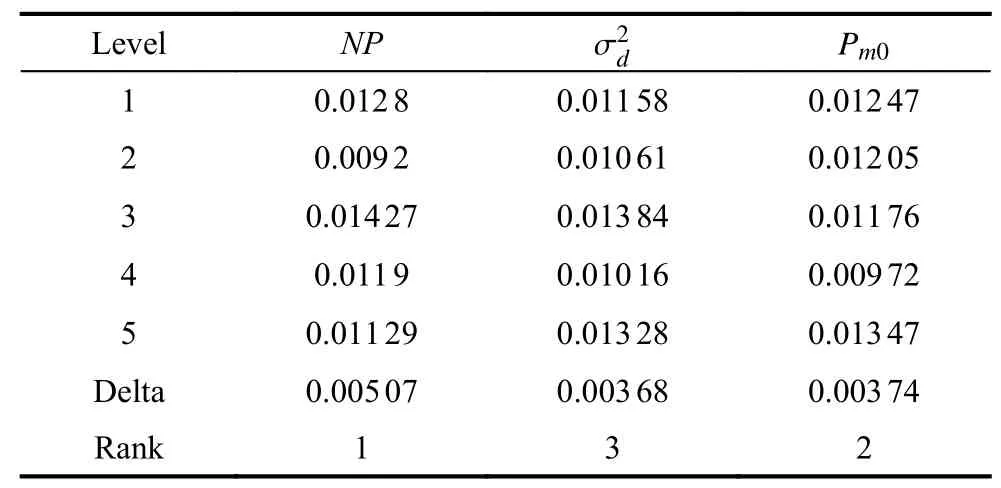
6.2 Parameters setting
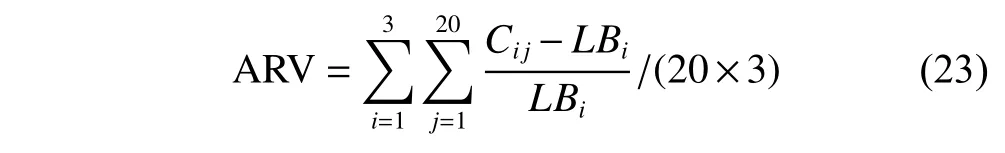
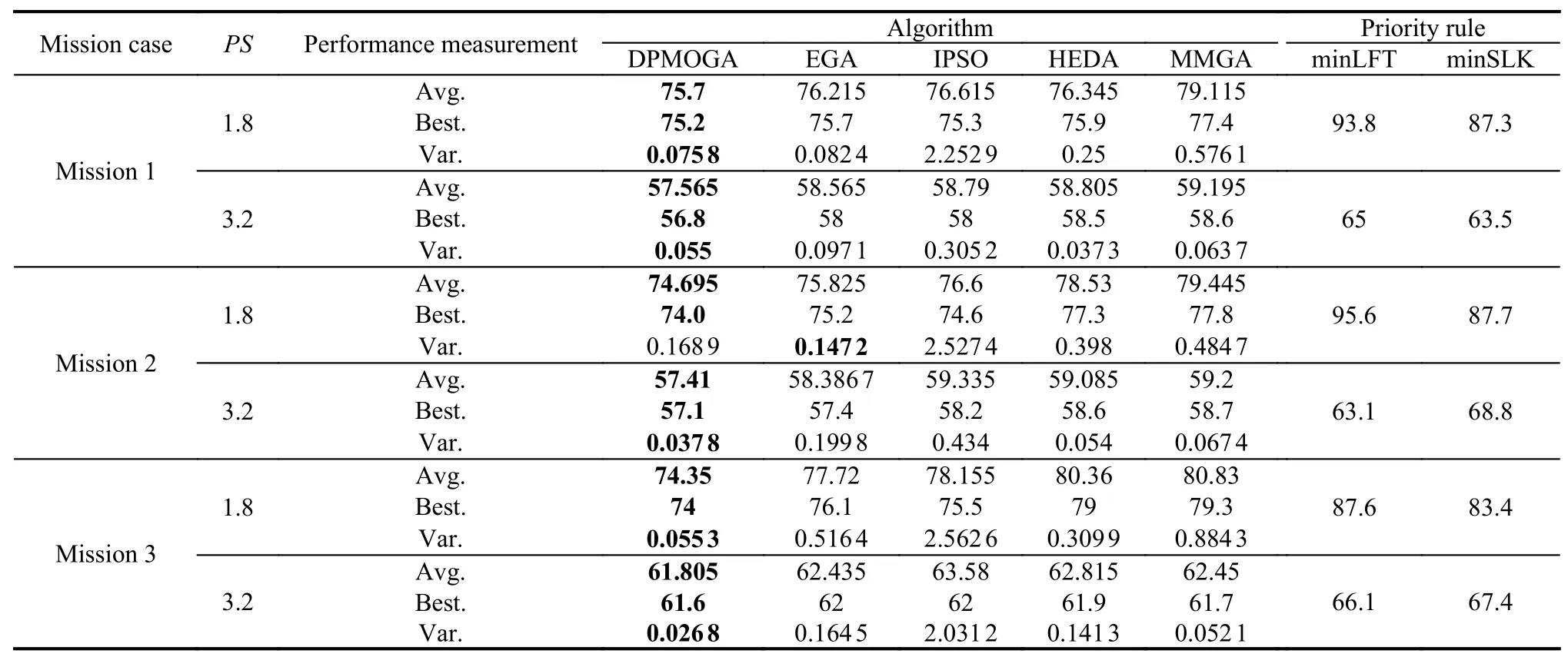
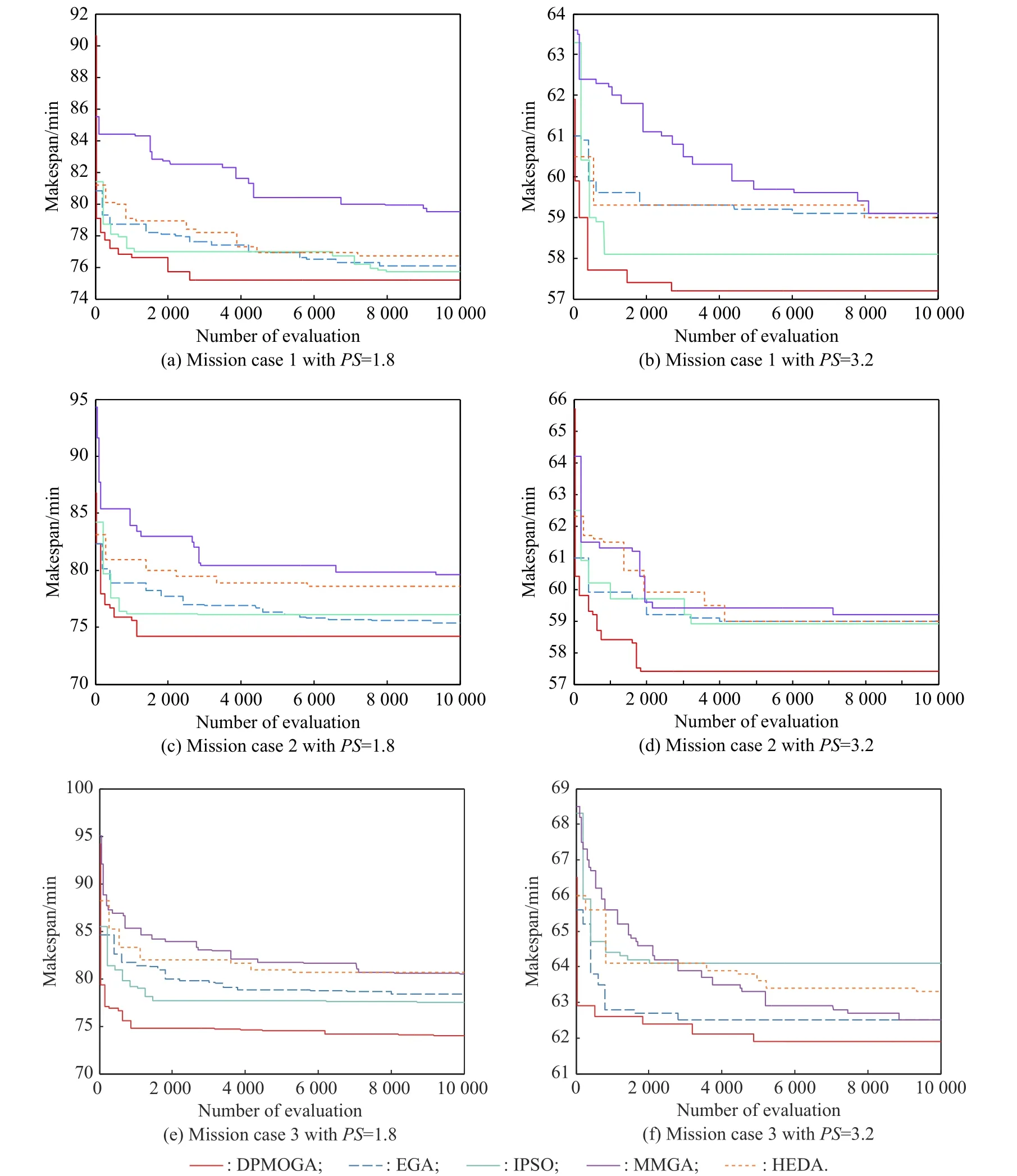
6.3 Comparisons with existing algorithms and discussion

7.Conclusion and future work
 Journal of Systems Engineering and Electronics2021年2期
Journal of Systems Engineering and Electronics2021年2期
