Observation scheduling problem for AEOS with a comprehensive task clustering

CHANG Zhongxiang ,ZHOU Zhongbao ,YAO Feng ,and LIU Xiaolu

1.School of Business Administration,Hunan University,Changsha 410082,China;2.Institute of Data Science and Decision Optimization,Hunan University,Changsha 410082,China;3.Department of Mathematics,Simon Fraser University,Surrey V3T 0A3,Canada;4.School of System Engineering,National University of Defense Technology,Changsha 410073,China

Abstract: Considering the flexible attitude maneuver and the narrow field of view of agile Earth observation satellite (AEOS)together,a comprehensive task clustering (CTC) is proposed to improve the observation scheduling problem for AEOS (OSPFAS).Since the observation scheduling problem for AEOS with comprehensive task clustering (OSWCTC) is a dynamic combination optimization problem,two optimization objectives,the loss rate (LR) of the image quality and the energy consumption (EC),are proposed to format OSWCTC as a bi-objective optimization model.Harnessing the power of an adaptive large neighborhood search (ALNS) algorithm with a nondominated sorting genetic algorithm II (NSGA-II),a bi-objective optimization algorithm,ALNS+NSGA-II,is developed to solve OSWCTC.Based on the existing instances,the efficiency of ALNS+NSGA-II is analyzed from several aspects,meanwhile,results of extensive computational experiments are presented which disclose that OSPFAS considering CTC produces superior outcomes.

Keywords:observation scheduling,comprehensive task clustering (CTC),bi-objective optimization,image quality,energy consumption (EC).

1.Introduction

Since the first Earth observation satellite (EOS) was launched by former Soviet Union in 1957 [1],the development of satellite technology has gone through more than half a century [2].The hardware performance has been greatly improved,and EOS has developed from the nonagile EOS [3]with only one degree of freedom to the semiagile EOS [4]with two degrees of freedom.Until now,a new generation of EOS named the agile Earth observation satellite (AEOS) was also launched [5],which had three degrees of freedom (pitch,roll,and yaw,see Fig.1).

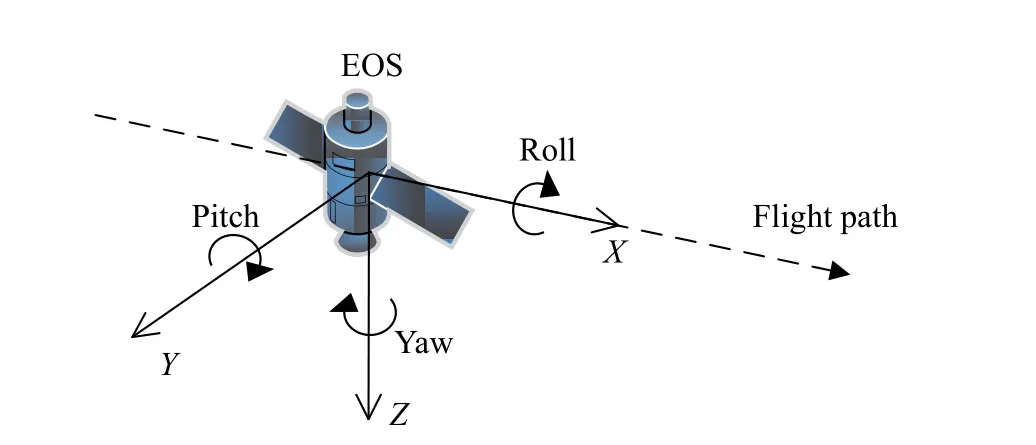
Fig.1 Three degrees of freedom for EOS

Because of the three degrees of freedom,the visible time windows (VTWs),the time period during which the ground targets are visible with AEOS,becomes much longer than the observation windows (OWs),the actual time period for observing ground targets,shown as in Fig.2.AEOS can observe ground targets before or after an upright pass (named the“nadir point”).

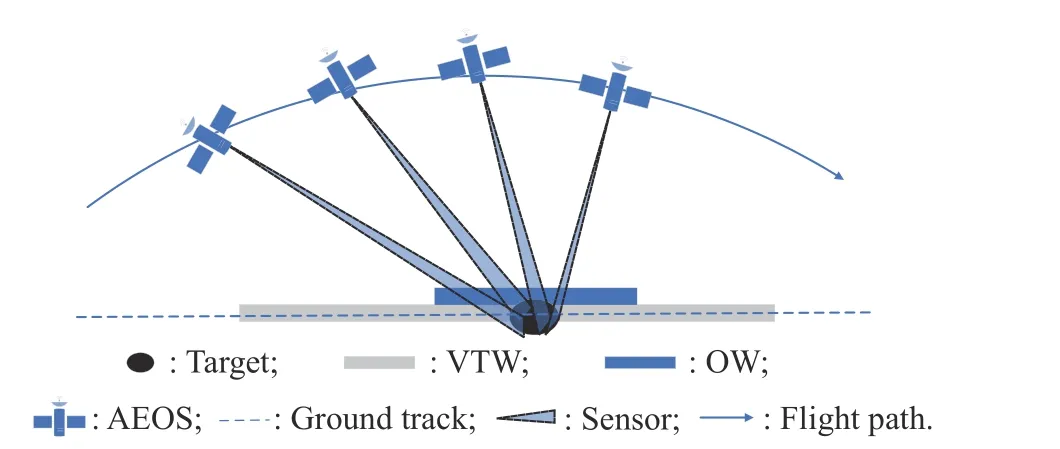
Fig.2 VTW and OW of AEOS

The tranditional observation scheduling problem for AEOS (OSPFAS) has been proven to be an NP-hard combinatorial optimization problem [6].Due to the complexity of OSPFAS,there exist almost researches considering observing the ground targets one by one.In other words,they did not consider task clustering [3].Lemaitre et al.[6]are pioneers in the research of the observation scheduling problem for AEOS.They just considered OSPFAS as a selecting and scheduling problem.Toward the PLEIADES project in France,they analyzed the complexity of OSPFAS and designed four heuristic algorithms to solve the problem.Many authors studied OSPFAS only considering small targets (point tasks or small areas) that AEOS can be observed in one pass[7−11].While,some other researches focused on the large targets [12,13],before observation scheduling,the large ground targets will be decomposed to several rectangle strips that can be observed in one pass.

Task clustering has been demonstrated as an effective strategy for improving the efficiency of the observation scheduling problem for EOS [3].Wu et al.published two papers about task clustering in 2013 [3]and 2017 [14].They [3]proposed a static two-phase scheduling method to split observation scheduling as the task clustering phase and the observation scheduling phase.In the second phase,considering overall tasks and obtained cluster-tasks together,they solved the observation scheduling problem.Then they [14]presented an adaptive simulated annealingbased scheduling algorithm integrated with a dynamic task clustering (ASA-DTC) strategy for replacing the static task clustering method.However,the satellites studied in both resaerches are all no agile EOS.There are two papers [15,16]studying the task clustering for AEOSs.However,frankly speaking,because the field of view of AEOS [17]is much narrower than that of no-agile EOS[18],the task clustering dependent on the wide field of view [3]may not be suitable for AEOS.Thus,we would like to propose a new comprehensive task clustering(CTC) for AEOS,and explore how to use it better.

Definition 1One on/off of the sensor is called an observation task.Note that,there may be a single ground target or several ground targets observed in a task.

On one hand,the CTC includes the task clustering proposed in 2013 [3]and 2017 [14],which depends on the satellite field of view to observe several ground targets in one pass,named the first type of CTC (see Fig.3 (a)).On the other hand,since restarting the sensor will spend several minters [17],SuperView-1 designs a novel mode for the sensor,in which the sensor will keep on but not observe,named the power-saving mode.For the mode,AEOS is not necessary to turn off the sensor after imaging every ground target,in other words,AEOS does not need to restart the sensor before imaging every ground target.Therefore,AEOS can observe serval ground targets by changing the attitude angle continuously,named the second type of CTC (see Fig.3 (b)).

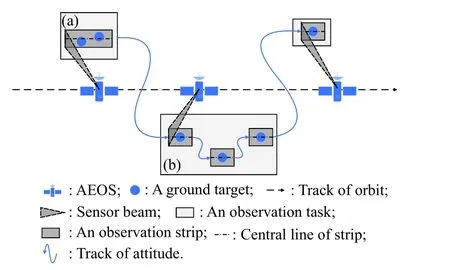
Fig.3 Task clustering for AEOS

The ground targets observed in the first type of CTC are not in their highest image quality moment,which we will define in a function later.In this way,the image quality of each ground target will decrease,which may be one main reason for image data decreasing after task clustering proposed in the research [14].While the image quality of each ground target observed in the second type of CTC does not decrease because they can be observed in their highest image quality moment,keeping the sensor in the power-saving mode will consume more energy.Given all that,CTC is not a process which has a hundred merits but not a single demerit.Optimizing the CTC to observe more ground targets but not increase energy consumption (EC) is the main focus in our paper.Due to the narrow field of view of AEOS mentioned above,the first type of CTC may not be suitable for AEOS,and we just consider the second type of CTC in our paper.

There are more choices and ways for observing ground targets because of the much longer VTW,but different observation moments obtain different image quality [19],named as time-dependent or profit-dependent in some existing researches [4,19−24].They proposed two similar functions to calculate the image quality.Liu [4]and He [23]thought the image qualityqbelonged to the interval [1,10]and was related to observation momentudefined as

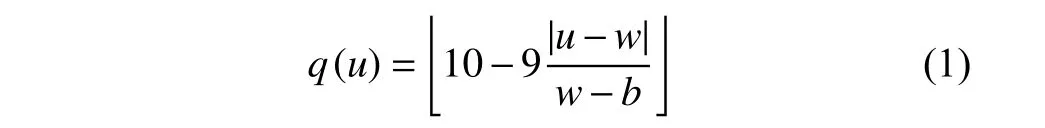
wherewdenotes the observation moment when the best image quality can be obtained.bis the begin time of the VTW that the observation belongs to.

Peng et al.[20,22]then referenced Liu [4]and He [23]and saw the image qualityqbelonged to the interval[0,1],defined as

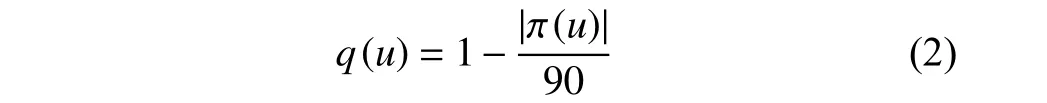
where π(u) denotes the pitch angle when AEOS observes the ground target at momentu.

Actually,(1) and (2) are the same in essence,which just consider the observation moment or the pitch angle,which is suitable for their study because they just consider observing ground targets one by one,but it may be not suitable for the problem considering CTC.Therefore,it is necessary to define a new function to calculate the image quality.

As mentioned above,AEOS has three degrees of freedom.The roll angle actually influences the image quality[3,14].Therefore,we consider the pitch angle and the roll angle to calculate the image quality of observation for AOESs as

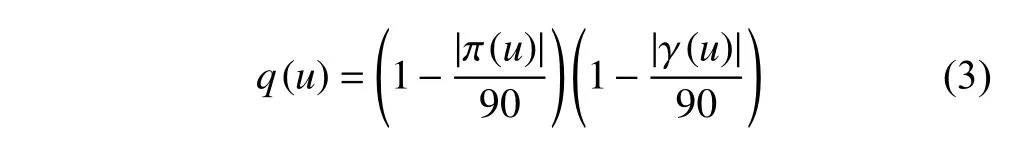
where π(u) and γ(u) denote the pitch angle and the roll angle respectively when AEOS observes the ground target at momentu.In addition,the image qualityq(u) belongs to the interval [0,1].Note that the bigger the value ofq(u) is,the better the image quality is.

The image quality of each ground target,as defined in(3),is dependent on the observation start moment.Meanwhile,the ground targets clustered in a clustering task and the EC of the clustering task,which will be explained in Subsection 2.2,are all dynamic.Thus,the observation scheduling problem for AEOS with comprehensive task clustering (OSWCTC) researched in our paper is a dynamic combination optimization problem.

In the next section,two important definitions of CTC and an equation for calculating the EC are proposed.Considering the EC and image quality as two objectives,OSWCTC is formated as a bi-objective optimization model in Section 3.Section 4 designs an adaptive large neighborhood search algorithm based on NSGA-II(ALNS+NSGA-II) to solve OSWCTC.Section 5 reports results of systematic experimental analysis carried out using our algorithm followed by concluding remarks in Section 6.

Throughout this paper,we represent variable and parameter names using one or more operators following the convention of object-oriented programming which we believe will improve the readability and help ease of presentation of this complex problem.Note that these variables/parameters can alternatively be represented by using one or more subscripts or superscripts.We prefer the object-oriented representation rather than the traditional mathematical representation of the constraints.For example,letSbe a parameter having attributesxandy.Then,xassociated withSis denoted byS.xandyassociated withSis denoted byS.y.This notational convention is used throughout this paper without additional explanations.

2.CTC

In this section,some assumptions and two definitions are proposed to restrain CTC.In addittion,a crucial method is proposed,which is used to calculate the EC after task clustering.

2.1 Preliminaries

To better solve the focus in our paper,several reasonable assumptions are proposed to standardize and simplify this problem referring to previous researches and engineering experiences.

Assumption 1Different types of satellites have different attributions,so we only consider an optical earth observation satellite,SuperView-1 [17].Frankly speaking,SuperView-1 is similar to AS-01 proposed in [4]and not a complete AEOS because it cannot image actively[2].Therefore,the yaw angle is not considered.

Assumption 2Because of the narrow field [17]of view of AEOS as mentioned in Section 1,the success probability of the first type CTC is too low,so we just consider the second type of CTC in our paper.

Assumption 3AEOS has sufficient on-board memory for each orbit,so it is not necessary to consider satellite image data downlink.

Assumption 4The ground targets considered are all spot targets or small ground targets which can be observed in one pass.Large ground targets need to be decomposed to some small ground targets before observation scheduling [12,13,25],which is irrelated to the focus in our paper.

Assumption 5Since the ground targets are redundant [26]according to the image capability of AEOS,we assume every ground target needs to be observed once at most.

Assumption 6We assume the time consumed by(re)starting the sensor is a constant variableTonand setTon=180 s.

Based on the aforementioned assumptions,the solution S for OSWCTC can be generally described by

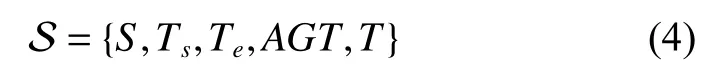
where the included notations are defined as follows:

(i)S={s,|S|=ns} is the set of satellites for observation scheduling.In this paper,we only consider Super-View-1,so we can ignore this attribute.

(ii) [Ts,Te]is the scheduling horizon for the OSWCTC.

(iii)AGT=indicates the set of all ground targets considered in observation scheduling,ngtmeans the quantity of all ground targets.Each targetgtiis

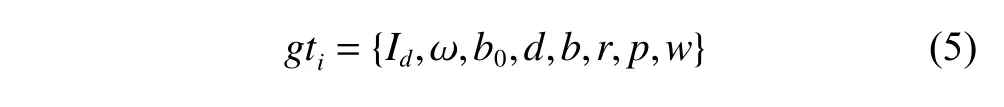
whereIdis the identifier ofgt,ω reflects the priority ofgti,b0is the best observation begin moment ofgti,dis the observation duration ofgt.bis the true observation begin moment ofgti,randpdenote the roll angle and pitch angle respectively according to the true observation begin momentb.wdenotes VTW ofgtiand is formatted as

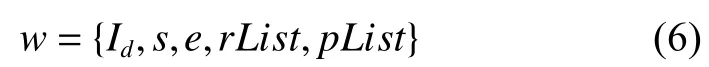
whereIdis the identifier ofwfor distinguishing several VTWs of a same ground target.Note that,a ground target with several VTWs will be clone as several ground targets with the same identifier but different VTWs.sandeare the visible begin time and the visible end time ofw.rListandpListindicate respectively the set of roll angles and pitch angles on different observation moment duringw.

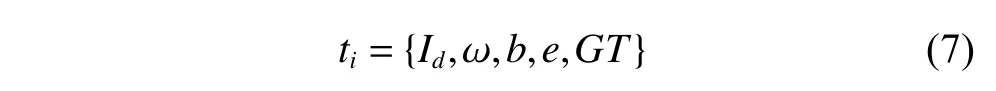
whereIdis the identifier ofti,ω reflects the total priority of the ground targets observed in the taskti,andbis the observation begin moment ofti,eis the observation end time ofti,andGTrepresents the set of all ground targets clustered and observed intiand all the targets are sorted ascending by their observation begin moment.

2.2 Two definitions about CTC

Definition 2The two adjacent ground targets should be clustered in the same task and observed together when the maximum interval time (MIT) between them is less thanTon.

As shown in Fig.4,MIT is the upper limit of the interval time between ground targets.If MIT of two ground targets is less thanTonand they are observed one by one,one of them will be abandoned for lacking time to turn on the sensor again.Instead,if we cluster them in the same task,it is possible for observing both of them.

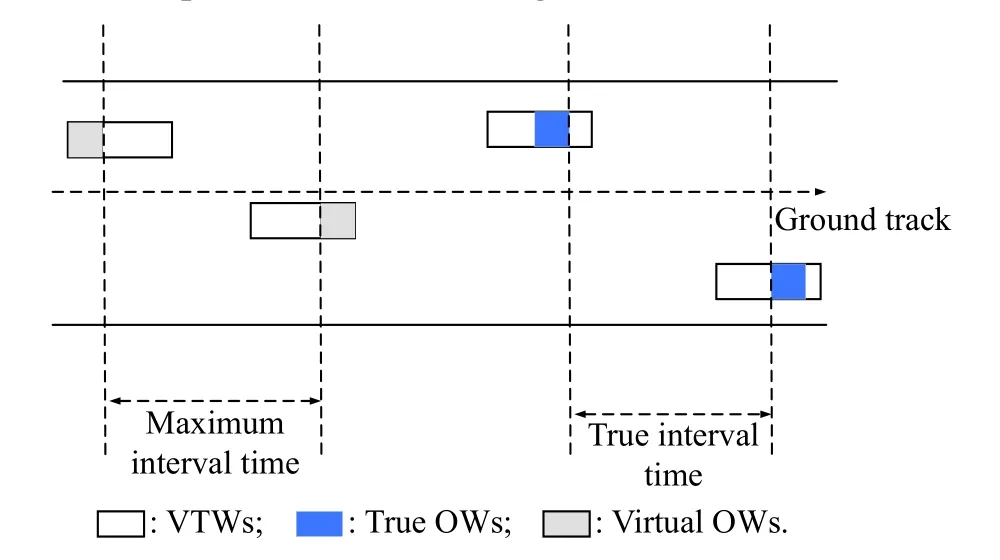
Fig.4 Maximum interval time and true interval time

Definition 3The two adjacent ground targets should be observed one by one when the true interval time (TIT)between them is bigger thanTon.

After observation scheduling,the true begin moment and the true end moment of observation for every ground target are confirmed.TIT is the interval time between the true observation moment of two ground targets,as shown in Fig.4.If they are clustered,the sensor will keep in the power-saving mode during TIT.According to EC which we will discuss in Subsection 2.3,when TIT between them is bigger thanTon,clustering them as an observation task is not inadvisable.

However,before the scheme is confirmed,we do not konw TIT for every ground target.Thus the two-stage method,first task clustering and then observation scheduling,adopted in the studies [3,14−16]is not suitable for our problem.Adopting CTC in observation scheduling will reduce the time of turning on/off the sensor and decrease the EC during the process of turning on the sensor,but keeping in the power-saving mode will consume more energy.These two contradictory processes result in that CTC must be fused into observation scheduling dynamically,which we will talk about in the problem modeling and algorithm designing.

2.3 EC in an observation task

In this section,four types of EC,turning on the sensor,keeping the sensor in power-saving mode,observation,and attitude conversion,of an observation task are described in detail.To facilitate to calculate these four types of EC,some notations are defined as below.

(i)Ei:Total EC ofti;

(ii)sti:Total time for keeping the sensor in power-saving mode ofti;

(iii)oti:Total observation time ofti;

(iv)cti:Total attitude conversion time inside ofti;

(v)et:EC by turning on the sensor;

(vi)es:EC rate for keeping the sensor in the powersaving mode for the sensor;

(vii)eo:EC rate for observation;

(viii)ec:EC rate for attitude conversion.

The total EC of the observation task is the sum of EC by turning on the sensor,EC by keeping in the powersaving mode for the sensor,EC by observation,and EC by attitude conversion,as defined by

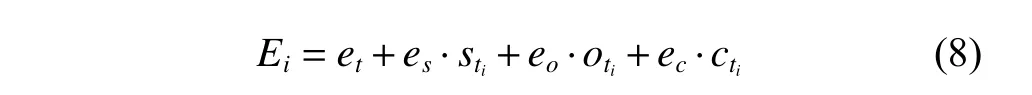
whereet,es,eoandecare constant variables,and according to engineering practice,et=1 J,es=0.01 W,eo=0.03 W,andec=0.05 W.The relationship between EC by turning on the sensor and the EC by keeping the sensor in the power-saving mode is shown in Fig.5.

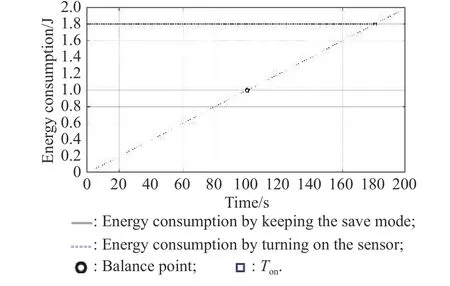
Fig.5 Relationship between the EC by turning on the sensor and the EC by keeping the sensor in the power-saving mode

According to Fig.5,when the total time for keeping the sensor in the power-saving mode is less than 100 s,the EC by keeping the sensor in the power saving mode is less than the EC by turning on the sensor.While,when the time exceeds 100 s,the EC by turning on the sensor is much less.Thus Definition 2 is reasonable.In addition,the calculation equations ofoti,stiandctiare proposed respectively as follows.

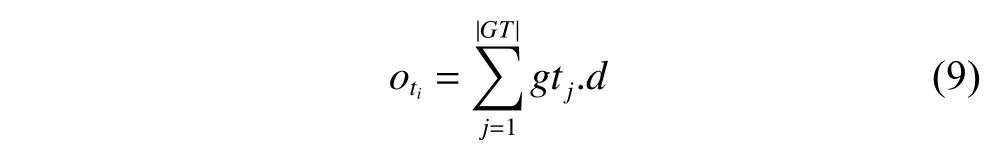
where |GT| denotes the number of ground targets clustered and scheduled to be observed in the taskti.gtj.dis the observation duration of each ground targetgtj.

I could say that a winter breeze had sent snow flurries dancing against our windowpane as we cuddled in front of a glowing fire, sipping1 spiced cider, alternately nuzzling each other and cooing about the depth of our love.

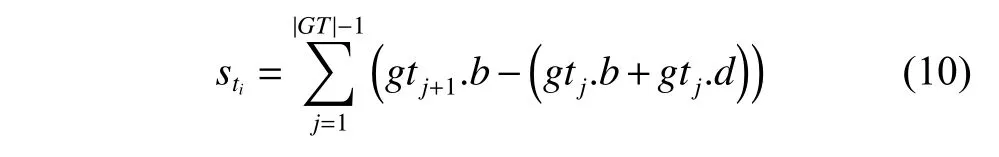
wheregtj.bdenotes the observation start moment of scheduled ground targetgtj.means the observation end moment of scheduled ground targetgtj.

SuperView-1 is similar to AS-01 proposed in the study[24],so we adopt the function (as defined in (11)) for calculating transition time from their research directly.

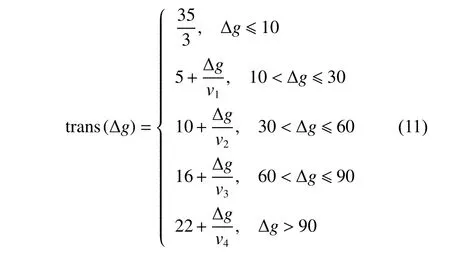
where the unit of transition time is second.v1,v2,v3andv4are four different angular transition velocities.And the angular velocity values arev1=1.5◦/s,v2=2◦/s,v3=2.5◦/s andv4=3◦/s . ∆gdenotes the total angle change between two observations and is calculated by

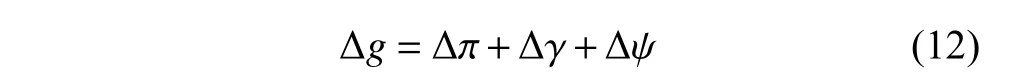
where ∆π,∆γ and ∆ψ indicate respectively the change of the pitch angle,the roll angle and the yaw angle.As mentioned in Assumption 1,the yaw does not change for each target,so (12) is transformed into

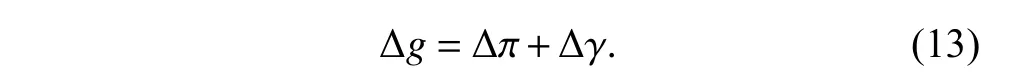
Take ∀gtj,gtj+1∈GTas examples,which are two adjacent scheduled ground targets in the taskti. ∆gfor two scheduled adjacent ground targets can be calculated by

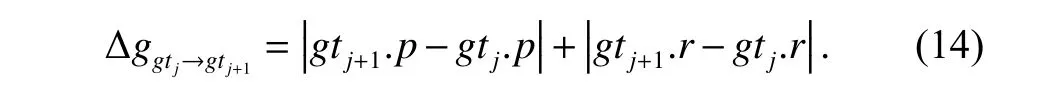
Therefore,the total attitude conversion time inside of the tasktican be calculated by

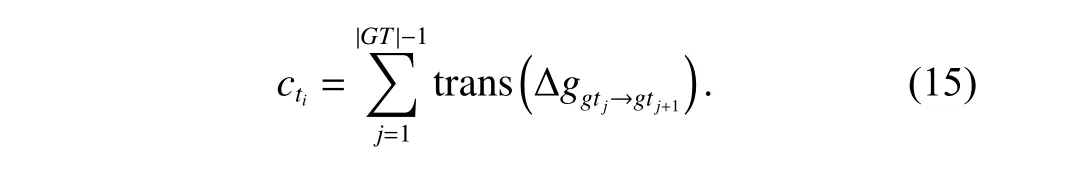
Whilesti,otiandctiare related to the scheduled targetsGT,which is dependent on the observation scheduling,it is a complex bi-objective optimization problem and will be discussed in the next section.

3.Analysis and modeling for scheduling

As mentioned above,it is impossible to fix the scheme of task clustering and then do observation scheduling,because both of them influence each other dynamically.Therefore,in this section,we analyze the problem in detail and formate a bi-objective optimization model considering task clustering and observation scheduling together.

3.1 Problem analyzing

However,the CTC is distinct from the traditional task clustering considered in previous studies.It cannot obtain several specific schemes of CTC before observation scheduling.Because of the capabilities of AEOS as mentioned in Section 1,both task clustering and observation scheduling influence each other,which results in that it has to solve them cooperatively.Two novel difficulties of the OSWCTC are as follows.

(i) For the dynamic of CTC,the ground targets clustered in CTC,the image quality of each ground target,and the EC of CTC,OSWCTC is more complex than the task clustering and observation scheduling studied in researches [3,14].

(ii) The studies [4,20,22−24]ignored the constraint for restarting the sensor,they thought the sensor was opening all-time in each orbit.It may be suitable for scenes where the distribution of ground targets is dense,but actually,ground targets are not always intensive in practical applications,which can be found from the instances designed in their papers.Therefore,the constraint for turning the sensor on should be considered.

All in all,OSWCTC is a novel problem and more complex than OSPFAS,which is a time-dependent problem[4,20,22−24]and is proved as an NP-hard problem [6].

3.2 A bi-objective optimization model

Four decision variables,nt,gtj.b,xjandxij,are considered in our model.As mentioned in Section 2.1,the decision variablentindicates the quantity of generated observation tasks.gtj.bdenotes the observation begin moment of each ground target,which belongs to its VTW([gtj.w.s,gtj.w.e]).Decision variablexjrepresents whether ground targetgtjis scheduled.And decision variablexijdenotes whether ground targetgtjis scheduled and clustered in taskti.We set

In addition,to facilitate to present the mathematical model,some notations and symbols are defined as below.

Observing as much ground targets as possible is the original intention of the observation scheduling problem for (A)EOS.Therefore,most authors consider maximizing the sum of priority of scheduled tasks or ground targets [4,20,22−24].Without loss of generality,we minimize the loss rate of image quality (LR) as one optimization objective function in our study,which is similar to maximizing the sum of image quality of the ground target scheduled to be observed.

f1(S),namely,LR,considers the priority and image quality of ground targets and belongs to the interval [0,1].

Spending less energy to observe more ground targets is a goal for observation scheduling [21].Therefore,we design another objective function named EC.Minimizing EC will observe the same quantity of ground targets by less energy,which is not only good for observation but also well for manegment of AEOS system.

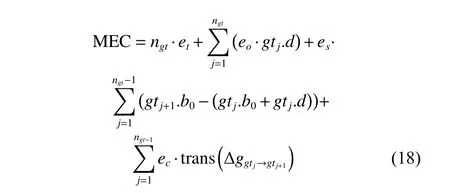
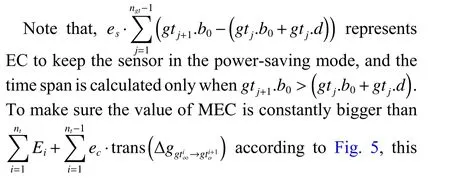
Given all that,we obtain two optimization objectives,LR and EC,as shown in (19).These two objectives are not irreconcilable in observation scheduling,so the dual optimization of them is reasonable and possible.OSWCTC is a bi-objective discrete optimization problem,which has disconnected nondominated solution sets [27].Then we will analyze and describe the constraints of OSWCTC.

The constraint (20) means all ground targets must be observed during their VTW.

It is an indisputable fact that the decision variable isntless than the t otal number of ground targetsngt.

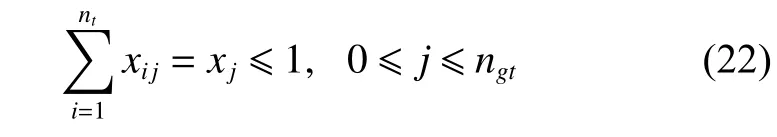
The constraint (22) means all ground targets can be observed one time at most,which is consistent with the assumption (5).

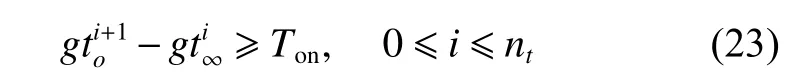
According to Definition 1,we know the sensor will be turned off after every observation task.Thus the interval timebetween two arbitrary adjacent observation tasks must be bigger than the time for restarting the sensor (Ton),which is al so consistent with Definition 2.

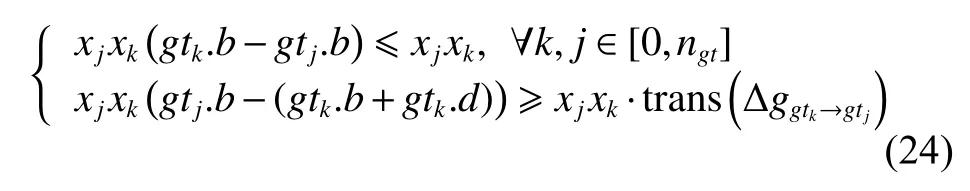
The two functions in (24) impose the transition time constraint.If and only if both ofxkandxjequal 1,the first function means there are two arbitrary observed ground targetsgtkandgtj,andgtkis observed beforegtj.And the second function represents the interval time between them must be bigger than the attitude conversion time from the ground targetgtkto the ground targetgtj.Otherwise,if any ofxkandxjequals 0,(24) will be invalid.

4.Description of our algorithm

The adaptive large neighborhood search (ALNS) algorithm can search for good quality solutions,which has been adopted in several studies [4,23,24]for solving OSPFAS.The basic structure of ALNS is double loops.The inner loop is a local search process,which consists of a destroy neighborhood and a repair neighborhood.The outer loop uses some criteria to control the search process.A score and a weight are assigned to each operator.An adaptive layer is included to update the weights and scores of different operators according to their performance for searching better solutions.And ALNS provides a flexible framework in which several different operators can be defined according to the characteristics of the problems.Therefore,we adopt ALNS as the basic algorithm for solving OSWCTC.

On the other hand,OSWCTC is a bi-objective optimization problem.Deb et al.[28]improved NSGA [29]and proposed NSGA-II in 2002,which is one of the best evolutionary multi-objective optimization algorithms so far[30].NSGA-II can obtain the Pareto frontier fast for the fast nondominated sorting approach,and they proposed a fast-crowded distance estimation and a simple crowded comparison operator to solve the defect of the evolutionary algorithm dependent on parameters.

Given all that,ALNS+NSGA-II is proposed.Note that,ALNS is used to generate offspring solutions while NSGA-II is for preserving elitist solutions fast.The basic structure of it is shown as Fig.6.

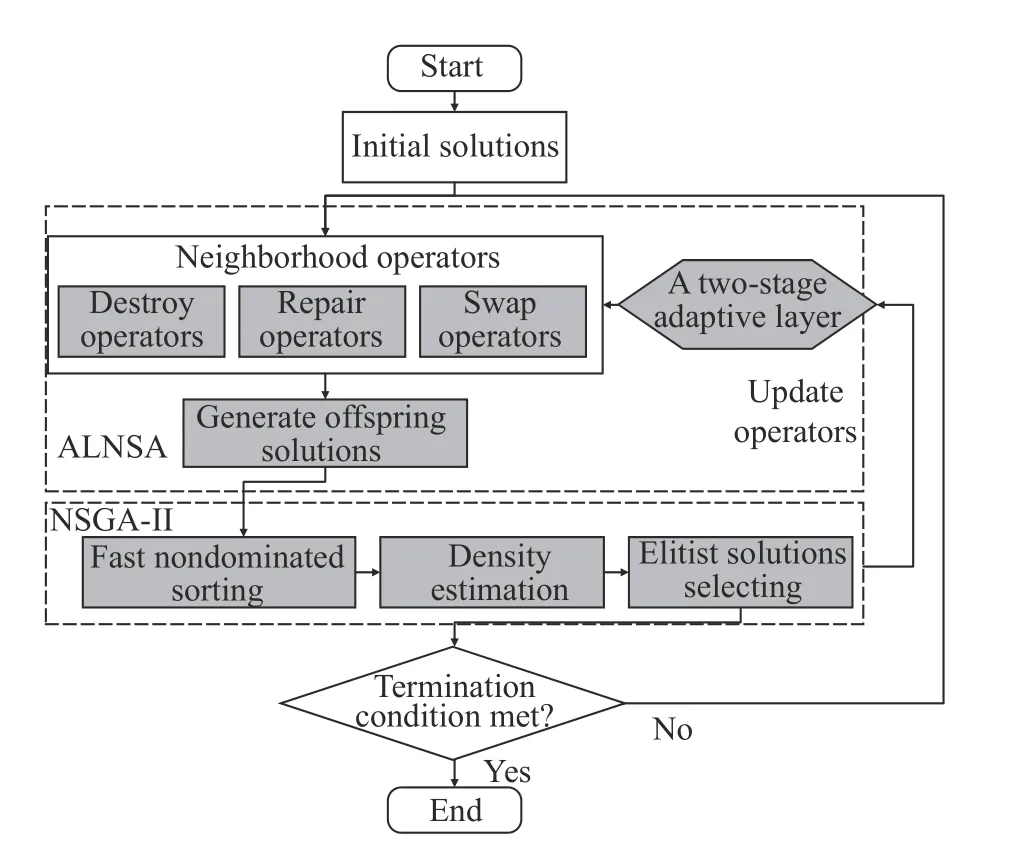
Fig.6 Basic structure of ALNS+NSGA-II

4.1 A random greedy heuristic algorithm (RGHA)

The much better initial solution is good for solving,though ALNS is not highly sensitive to the initial solution.Since the greedy heuristic strategy can find a stable and nice solution,we desgin an initialized algorithm based on the greedy heuristic.Considering the characteristic of OSWCTC,there are two main stages,confirming the observed moment and clustering the tasks,considered in RGHA,and the pseudocode of which is shown as follows.

The ground targets are redundant [26]according to the image capability of AEOS,so a partIGTofAGTis chosen in line 2,and considering the diversity of solutions,every ground target is selected randomly.In line 6,the observation moment with the best image quality for each ground target is visited in priority.And we do not consider moving observation moment backward or forward [4]in confirming observed moment (line 4 − line 8).In clustering task (line 9 − line 11),after confirming the observation start moment of each scheduled ground target,we can cluster ground targets and generate tasks(single task or clustering task) according to Definition 2.RGHA can obtain many different solutions fast,which is good for searching all space of solution and avoid falling into local optimum.

4.2 Two categories of operators

Considering the characteristic of OSWCTC,two categories of operators are designed.The operators in the first category process the solution one by one and try to improve the solution,named“Destroy &Repair”.And it is similar to operators in [4],there are two types of operators,destroy operators and repair operators.Destroy operators are used to delete some observed ground targets from a given solution,and repair operators are used to inserting some unscheduled ground targets into the solution,and in the way,a new solution is generated.And a box-method [31],which we will describe in Subsection 4.3 in detail,is adopted to decide whether the new solution is accepted or not.

There are two operators,SO-Target and SO-Task,in the second category,which are carried out based on the elitist solutions,named“Swap”.We cross some parts of two different elitist solutions to generate two new solutions.According to the box-method,we decide whether the new solutions are accepted or not.

4.2.1 Destroy operators

Since there are two objects,ground targets,and tasks,in OSWCTC,we design two kinds of destroy operators toward ground targets and tasks respectively.The first kind of destroy operators remove some observed ground targets without considering the relationship between them,while the second kind of destroy operators remove some ground targets by removing some tasks directly.The removed ground targets are saved into a set called taboo listQwith a given size of |Q|,all ground targets in which will not be considered when executing repair operators.Qis empty before removing ground targets and fillingQto the full is the termination condition for destroy operators.And we save all unscheduled ground targets in a set denoted byF.The ground targets inFbut not inQwill be reinserted to produce a new solution.The two kinds of destroy operators and eight different destroy operators are defined as follows.

(i) Destroy operators handling ground targets directly

RD-Target:This operator selects some scheduled ground targets from a given solution randomly and removes them.

PD-Target:The guidance information for this operator is the priority of each target.This operator selects some scheduled ground targets with the lowest priority from a given solution and removes them.

LD-Target:The guidance information for this operator is the length of VTW for each target.This operator selects some scheduled ground targets with the longest VTW from a given solution and removes them.

CD-Target:The guidance information for this operator is the conflict degree [4]of each target.This operator selects some scheduled ground targets with the largest conflict degree from a given solution and removes them.

(ii) Destroy operators handling tasks directly

RD-Task:This operator selects some tasks from a given solution randomly and removes the ground targets observed in these tasks.

PD-Task:The guidance information for this operator is the profit of each task.This operator selects some tasks with the lowest profit from a given solution and removes the ground targets observed in these tasks.

ED-Task:The guidance information for this operator is the EC of each task.This operator selects some tasks with the largest EC from a given solution and removes the ground targets observed in these tasks.

CD-Task:The guidance information for this operator is the conflict degree of each task,which is the total of the conflict degree of ground targets observed in it.This operator selects some scheduled tasks with the largest conflict degree from a given solution and removes the ground targets observed in these tasks.

4.2.2 Repair operators

The repair operators will be used in pairs with the destroy operators.There are two types of repair operators considering different searching neighborhoods (SN).SN of the first type of repair operators is the set of unscheduled ground targets,the VTW of which is located in the OW of tasks in a given solution,called“Inside”.While SN of the second type is the set of unscheduled ground targets,the VTW of which is located in the time span between every two adjacent tasks in a given solution,called“Outside”.The two types of repair operators and eight different repair operators are defined as follows.

RR-Inside/RR-Outside:These operators insert some unscheduled ground targets from SN (Inside/ Outside),inFbut not inQ,into the given solution randomly.

PR-Inside/PR-Outside:The guidance information for these operators is the priority of each target,these operators select some unscheduled ground targets with the biggest priority from SN (Inside/ Outside),inFbut not inQ,into the given solution.

LR-Inside/LR-Outside:The guidance information for these operators is the length of VTW for each target,these operators select some unscheduled ground targets with the shorter VTW from SN (Inside/ Outside),inFbut not inQ,into the given solution.

CR-Inside/CR-Outside:The guidance information for these operators is the conflict degree of each target,these operators select some unscheduled ground targets with the smaller conflict degree from SN (Inside/ Outside),inFbut not inQ,into the given solution.

4.2.3 Swap operators

The first category operators generate a new solution one time by changing some part of one solution,while the second category operators,swap operators,generate two solutions one time by crossing some part of two different elitist solutions.Facing ground targets and tasks respectively,SO-Target and SO-Task are proposed.

SO-Target:This operator has three steps.In the first step,it will select two arbitrary different elitist solutions as parent solutions.Then it will cross some ground targets in two parent solutions randomly and generate two new offspring solutions.In the end,using the box-method to decide whether the new solutions are accepted or not.

SO-Task:This operator is similar to SO-Target,but the second step of this operator is different from that of SOTarget.It will select some tasks and cross the ground targets observed in these tasks.

4.3 A variation of the box-method

The box-method [31]based on the ε-constraint method is well known in solving multi-objective discrete optimization problems.It guides the evolution in the non-dominated region,and it is very useful in obtaining the Pareto frontier faster.On the other hand,the box-method does not decrease the diversity of solutions.

4.4 A two-stage adaptive layer

Each operator has a score and a weight.Because of the classification of operators,we design a two-stage adaptive layer for updating the weight of each operator.The first stage adaptive layer is to control the utilized rate of“Destroy &Repair”and“Swap”,and the second stage is proposed for selecting the operators in every production.The score depends on the past performance of observation scheduling,and the weight is updated according to the score.Here,the four scores are defined as

(i) σ1:A new solution dominates all current solutions;

(ii) σ2:A new solution dominates one of the current non-dominated solutions;

(iii) σ3:A new solution in the current Pareto frontier;

(iv) σ4:A new solution is dominated by one of the current non-dominated solutions.

At the end of iteration,the weights are updated:

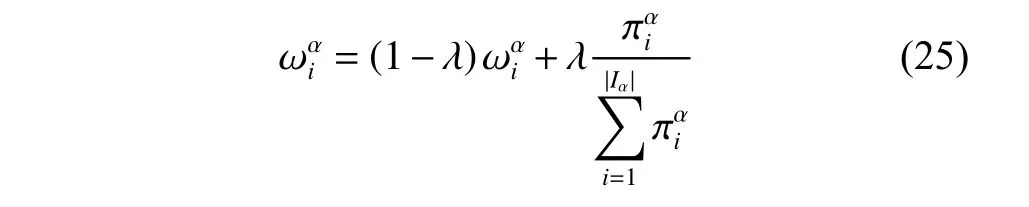
where α denotes the category/type of the operator.α=in the first stage,and α=in the second stage.|Iα| represents the number of operators in different categories/types.denote the score and weight according to the operator.λ ∈[0,1]is a reaction factor which controls how sensitive the weights are to changes in the performance of operators.A value of 0 means that the weights remain unchanged,while a value of 1 implies that the historic performance has no impact:the weight only depends on the current score of the operator.

The roulette wheel mechanism is used to choose the assignment operators.The utilized ratethat operatoriwill be selected is calculated according to the following equation:

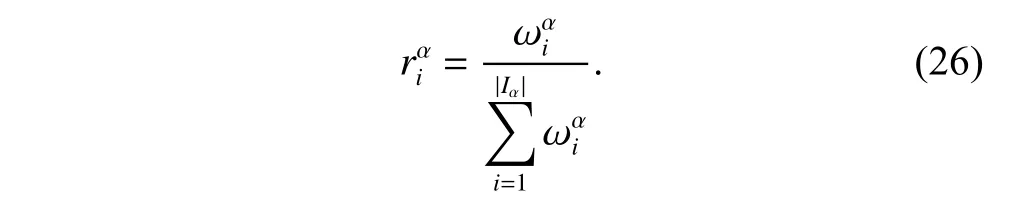
The maximum number of iterations,denoted by Max-Iter,is the only terminational criterion for ALNS+NSGAII.The value MaxIter is given before every evolution step.

5.Computational experiments

The influence of CTC on OSPFAS will be explored in detail.Before that,we first analyze the efficiency of our algorithm,ALNS+NSGA-II,form several aspects.Note that,we code our algorithm in C#,using Visual Studio 2013,and perform all simulation experiments on a laptop with Intel(R) Core (TM) i7-8750H CPU @ 2.2GHz and 16 GB RAM.Since SuperView-1 is similar to AS-01 proposed in studies [4,24],we take all simulation instances,Chinese area distribution (CD) and worldwide distribution (WD),proposed in Liu [4]as benchmark data to carry out our experiment,the details of which can be checked in research [4].In addition,there are general parameters of the ALNS+NSGA-II algorithm shown in Table 1.

Table 1 General parameters

5.1 Analysis of the evolution of operators

To analyze the evolution of each operator,i.e.,the changing process of their weights,we choose CD-50 in the CD as a test case.The value of the reaction factor λ apparently affects the evolution of each operator according to (25),so we first analyze the evolution of each operator under different λ ∈[0,1],named“parameter optimization”.Then based on the result of“parameter optimization”,the evolution of each operator is displayed,named“operator evolution”.

5.1.1 Parameter optimization

To analyze the influence of different values of λ ∈[0,1]to the evolution of each operator,we set MaxIter=200,and show the weight of each operator after algorithm terminated in Fig.7.Note that,thex-axis andy-axis denote the value ofλand the weight respectively.

The weight of operators in“Destroy &Repair”is always bigger than that of operators in“Swap”.Note that,when λ=0.5,the effect of two categories operators are the closest,while the SO-Target operator is constantly better than the SO-Task according to any value of λ.

On the other hand,the weight of operators in“Destroy &Repair”is irregularly changed according to different values of λ.In order to make sure more operators can contribute to the ALNS+NSGA-II algorithm,we set λ=0.5 i n the following experiments.

Fig.7 Weight of each operator being evolutional under different values of λ

5.1.2 Operator evolution

We set MaxIter=1 000 to obtain more date of the weight of each operator,and according to the first experiment,we set λ=0.5.From Fig.8,we can find after the 100th iteration the weight of operator becomes stable,the weight of“Destroy &Repair”operators is stable around 0.513 6,while that of“Swap”operators is stable around 0.486 4.Therefore,the effect of“Destroy &Repair”operators are constant slightly better than that of“Swap”operators.

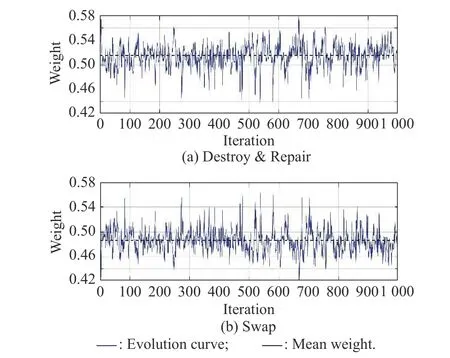
Fig.8 Evolution of two categories operators in the first stage

Fig.9 and Fig.10 represent the evolution of“Destroy”operators and“Repair”operators respectively.When the value of the reaction factor λ equals 0.5,the evolution of each operator is relatively stable after the 10th iteration.

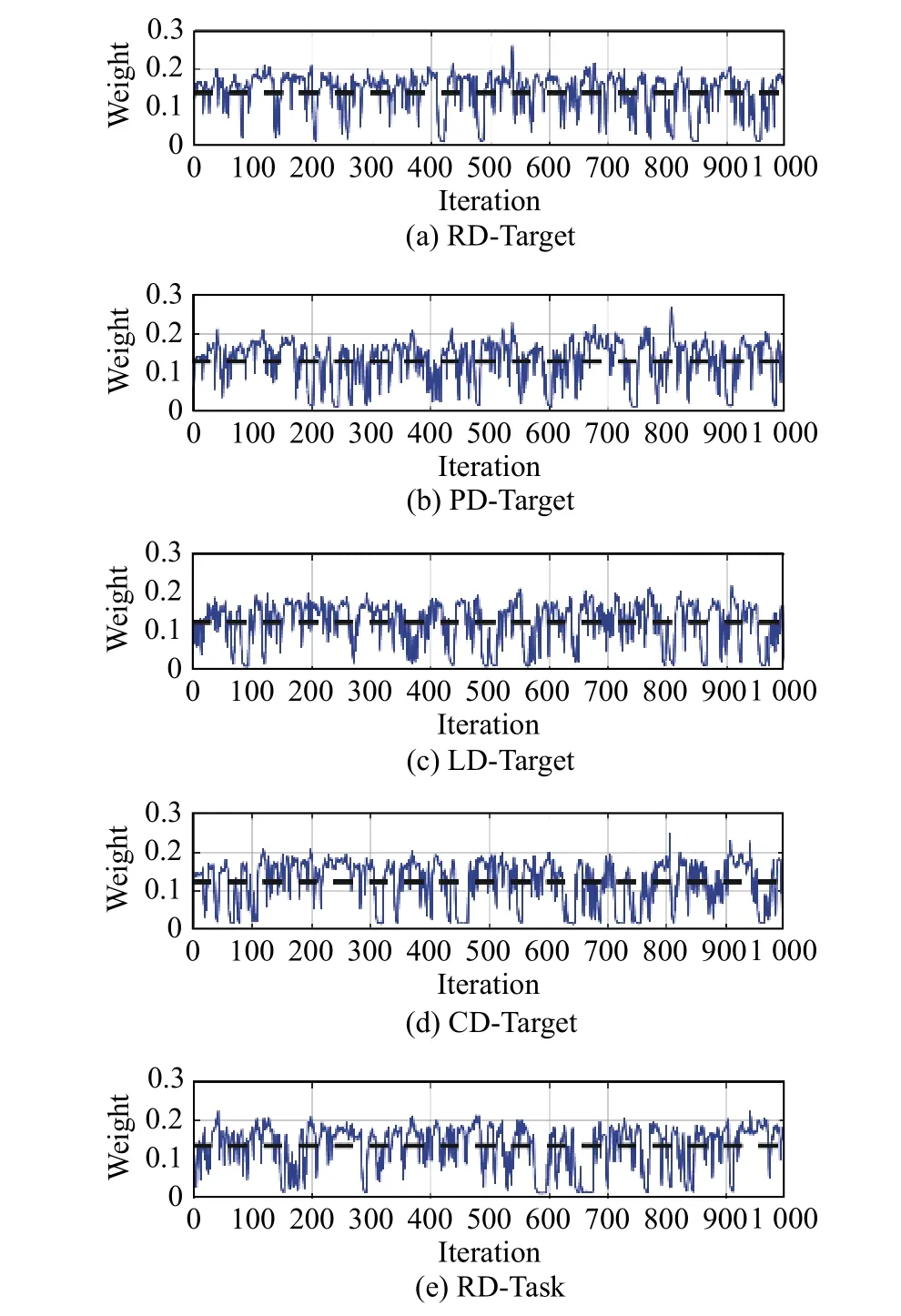
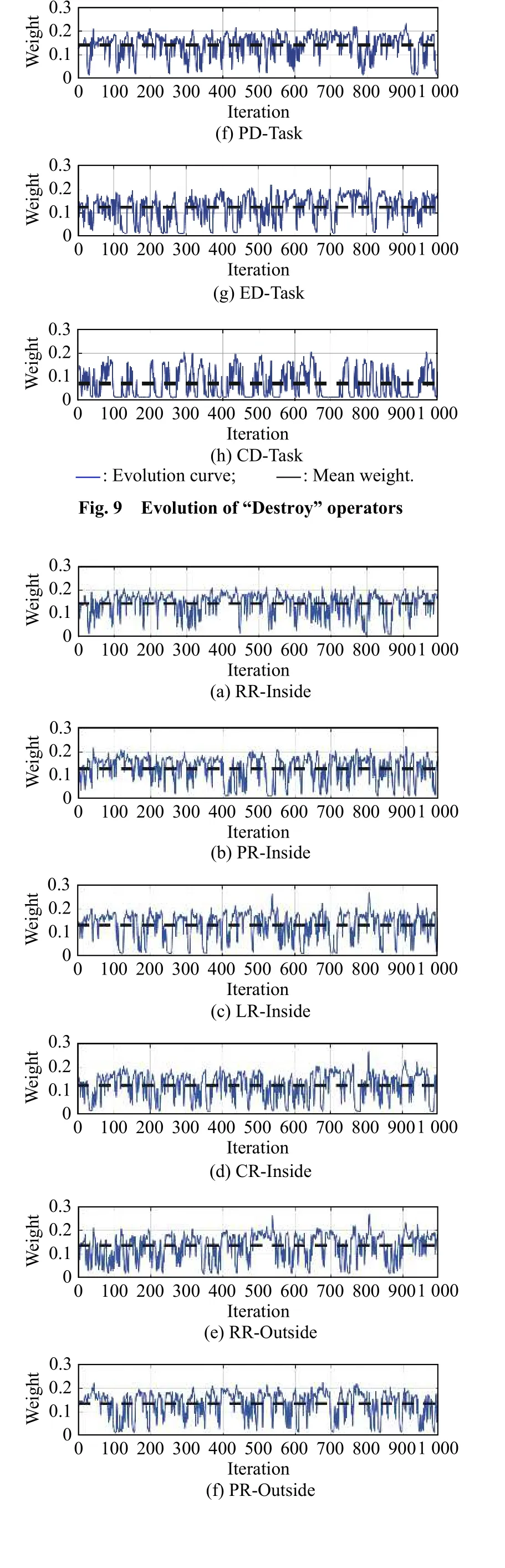
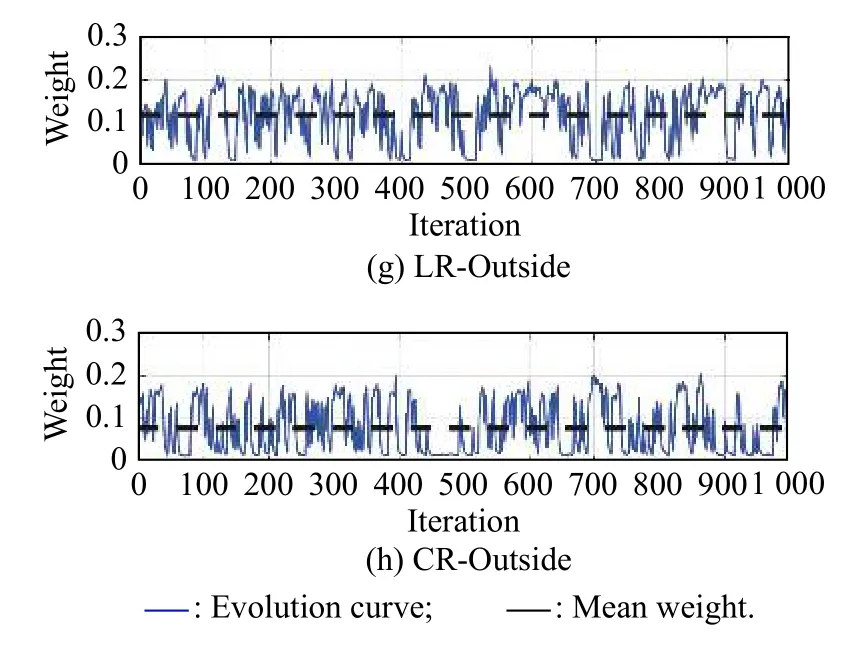
Fig.10 Evolution of“Repair”operators

Among the“Destroy”operators,the mean weight of PD-Task (0.1414) is the best and the mean weight of CDTask (0.0742) is the worst.While the mean weight of RRInside (0.1457) is the best and the mean weight of CROutside (0.0785) is the worst among the“Repair”operators.As mentioned in Subsection 4.2.2,the operators in“Destroy”and that in“Repair”should be used in pair,according to Fig.9 and Fig.10,we can find the pair of operators coupled by PD-Task and RR-Inside is always the most effective,which is very helpful for constructing a feasible solution within a very short time,especially in an engineering environment.Though the effect of“Swap”operators is slightly worse than that of“Destroy &Repair”operators as shown in Fig.8,the“Swap”operators generate offspring solutions based on the history of elitist solutions,which is a good addition for“Destroy &Repair”.

The evolution of two operators in“Swap”is shown in Fig.11.The effect of SO-Target is significantly better than that of SO-Task,which is consistent with the phenomenon as shown in the third subplot in Fig.7.After the 10th iteration,the weight of SO-Target (around 0.9182)is constantly greater than that of SO-Task (around 0.0831).

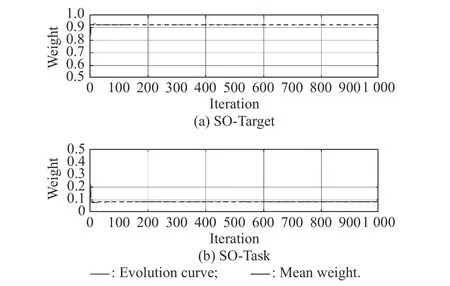
Fig.11 Evolution of swap operators

5.2 Efficiency of ALNS+NSGA-II

The ability and stability [28,32]for searching the better solutions are two important indicators to evalute the efficiency of multi-objective optimization algorithms.Without loss of generality,in this section,we also analyze the efficiency of ALNS+NSGA-II from these two aspects.

5.2.1 Ability for searching

All operators are proposed in our paper considering the characteristics of OSWCTC,so we do not compare our ALNS+NSGA-II algorithm with the existing algorithm(ALNS [4]) directly,but just compare RGHA which is used to construct initial solutions for ALNS+NSGA-II with ALNS to explain the effectiveness of our ALNS+NSGA-II algorithm.In order to compare with ALNS,we will simplify OSWCTC without considering the constraint (23) and observing ground targets one by one.Undoubtedly,ALNS must be better than RGHA,for RGHA without considering any iteration and operator.On the other hand,RGHA also should be simplified as the following several aspects:

(i) We set BMR=1 without considering image quality for observation,in other words,we adopt maximizing the total reward of the observed ground targets proposed in [4]as the optimization objective,which does not consider image quality and EC.

(ii) SetTon=0 in Definition 2,in this way,the constraint (23) will be invalid,which means the sensor is always on during the whole scheduling horizon.

(iii) Set the population of solutionNS=1.RGHA just generates a single solution for each scenario.

(iv) We setRS=1 to select all ground targets fromAGTfor observation scheduling,which will change line 2 in 0 to“select all ground targets inAGT”.

All the scenarios in WD proposed in the study [4]are adopted,and the comparing results are shown in Table 2.Rpdenotes the ratio for the observed profit which is the percentage of the obtained profit in the total potential profit obtained by RGHA.represent the maximum ratio,average ratio and minimum ratio obtained by ALNS respectively.runTdenotes the running time of the two algorithms,the unit of which is second.AndGrepresents the obtained profit ratioGpbetweenRpandand the running time ratioGtbetween theirrunT.

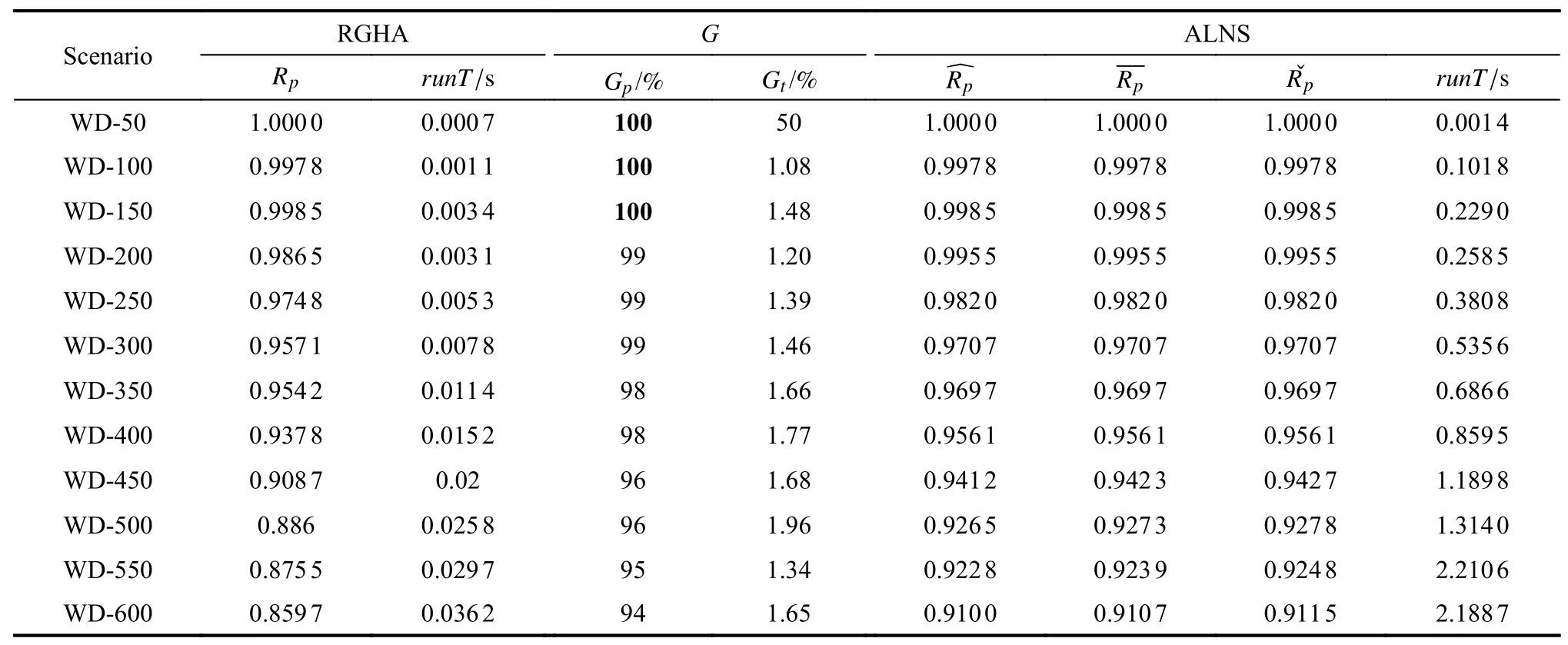
Table 2 Comparing results

It is apparent that the solutions obtained by ALNS are better than that obtained by RGHA,but the solutions obtained by RGHA are acceptable.The profit ratioGpbetween them is bigger than 94% for all scenarios.Thus,our RGHA can search for a relatively well solution for every scenario.On the other hand,RGHA can obtain the related well solution in several dozens of milliseconds at most and is much faster than ALNS,therefore RGHA is very helpful for constructing a well feasible solution within a very short time,especially in an engineering environment.

5.2.2 Stability for searching

Since some evidence shows that the random search can be competitive to evolutionary approaches in multi-objective spaces [33−35],we propose a very crude random evolutionary mechanism (CREM),in which the elitist solutions are preserved randomly,to analyze the evolutionary mechanism,NSGA-II,in our algorithm.Then we combine random evolutionary mechanism (REM) with ALNS (ALNS+CREM) as the control algorithm.

Eight simulation instances,CD-50−CD-400,with an increasement step of 50,from CD are considered as test cases,the values of hypervolume (HV) during 200 iterations based on ALNS+NSGA-II and ALNS+CREM are shown in Fig.12.Note that,HV is calculated by an influential algorithm,HV by slicing objectives (HSO) [36,37].

The black dotted line denotes the iterations HV obtained by ALNS+NSGA-II,while the blue dotted line denotes the iterations HV obtained by ALNS+CREM.

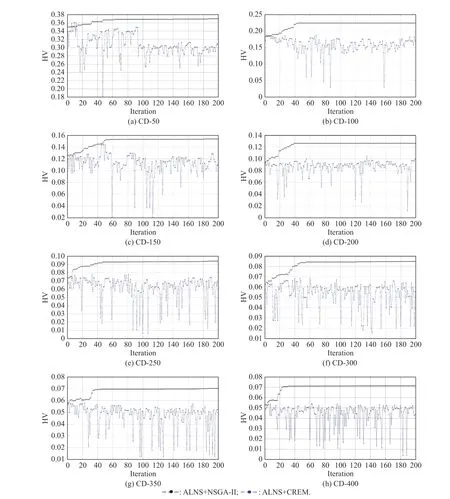
Fig.12 Values of HV during 200 iterations obtained by ALNS+NSGA-II and ALNS+CREM

It is apparent that the value of HV obtained by ALNS+NSGA-II always reaches a stable value after about 50 iterations for these eight simulation instances,while the value of HV obtained by ALNS+CREM is always in a disorder state.To illustrate this phenomenon in depth,based on all simulation instances in WD,restart these two algorithms,ALNS+NSGA-II and ALNS+CREM,respectively for 50 times,and draw a boxplot of HV obtained by them as shown in Fig.13.The black boxes and blue boxes denote the HV obtained by ALNS+NSGA-II and ALNS+CREM,and the red pluses indicate the outliers.In addition,in order to display the efficiency of NSGA-II more visually,we also plot the best Pareto frontiers of six specific simulation instances,WD-100,WD-200,WD-300,WD-400,WD-500 and WD-600,during 50 times restarting with an increasement step of 100.

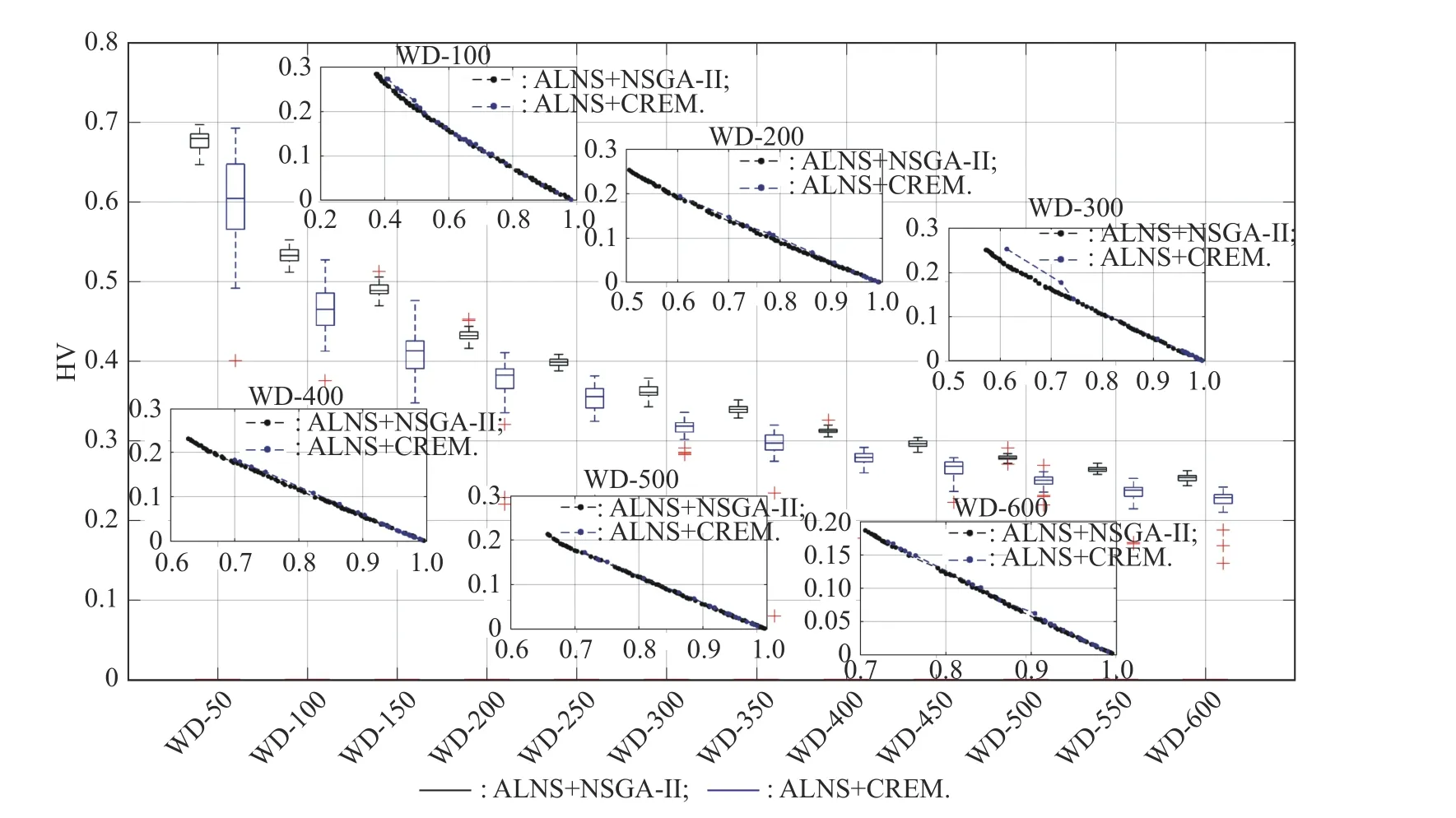
Fig.13 Values of HV obtained by ALNS+NSGA-II and ALNS+CREM

Firstly,it reflects the nondominated solution obtained by ALNS+NSGA-II is better than the nondominated solution obtained by ALNS+CSEM constantly that the location of black boxes is always higher than the location of blue boxes for all simulation instances.

Secondly,the length of black boxes is significantly shorter than that of blue boxes,and the quantity of red pluses for black boxes is always smaller than that for the blue boxes,both of which reflect ALNS+NSGA-II can achieve the nondominated solutions stably.

Thirdly,toward five specific simulation instances,the location of Pareto frontiers also reflects that NSGA-II is a nice evolutionary mechanism.On the one hand,the location of Pareto frontiers obtained by ALNS+NSGA-II is always under that obtained by ALNS+CSEM.On the other hand,Pareto frontiers obtained by ALNS+NSGA-II is also much longer.The longer the Pareto frontier is,the more diverse the solutions are.

All in all,considering both of the efficiency and the convergence,our algorithm,ALNS+NSGA-II is a nice evolutionary algorithm for solving the OSWCTC,that is,ALNS+NSGA-II could reach the better solutions stably.

5.3 Efficiency of CTC

To analyze the efficiency of CTC,two control groups are proposed.Every ground target is observed one by one and after each observation,the sensor must be closed after each observation and need to be reopened before every observation,named as close the sensor after each observation (CSEO),while the sensor is always on during the whole scheduling horizon in the other control group,named as keep the sensor opening all time(KSOA).In other words,it is not necessary to close or reopen the sensor for every observation in KSOA.We call the experimental group as CTC.In addition,we adopt all scenarios in CD as study cases and run our ALNS+NSGAII algorithm to solve them under these three groups,CTC,CSEO and KSOA.According to the comparing results,as shown in Table 3,several interesting conclusions can be obtained.represent the maximum value,average value and minimum value of the first objective(LR) in the Pareto frontier respectively,whileandrepresent the maximum value,average value,and minimum value of the second objective (EC) in the Pareto frontier respectively.

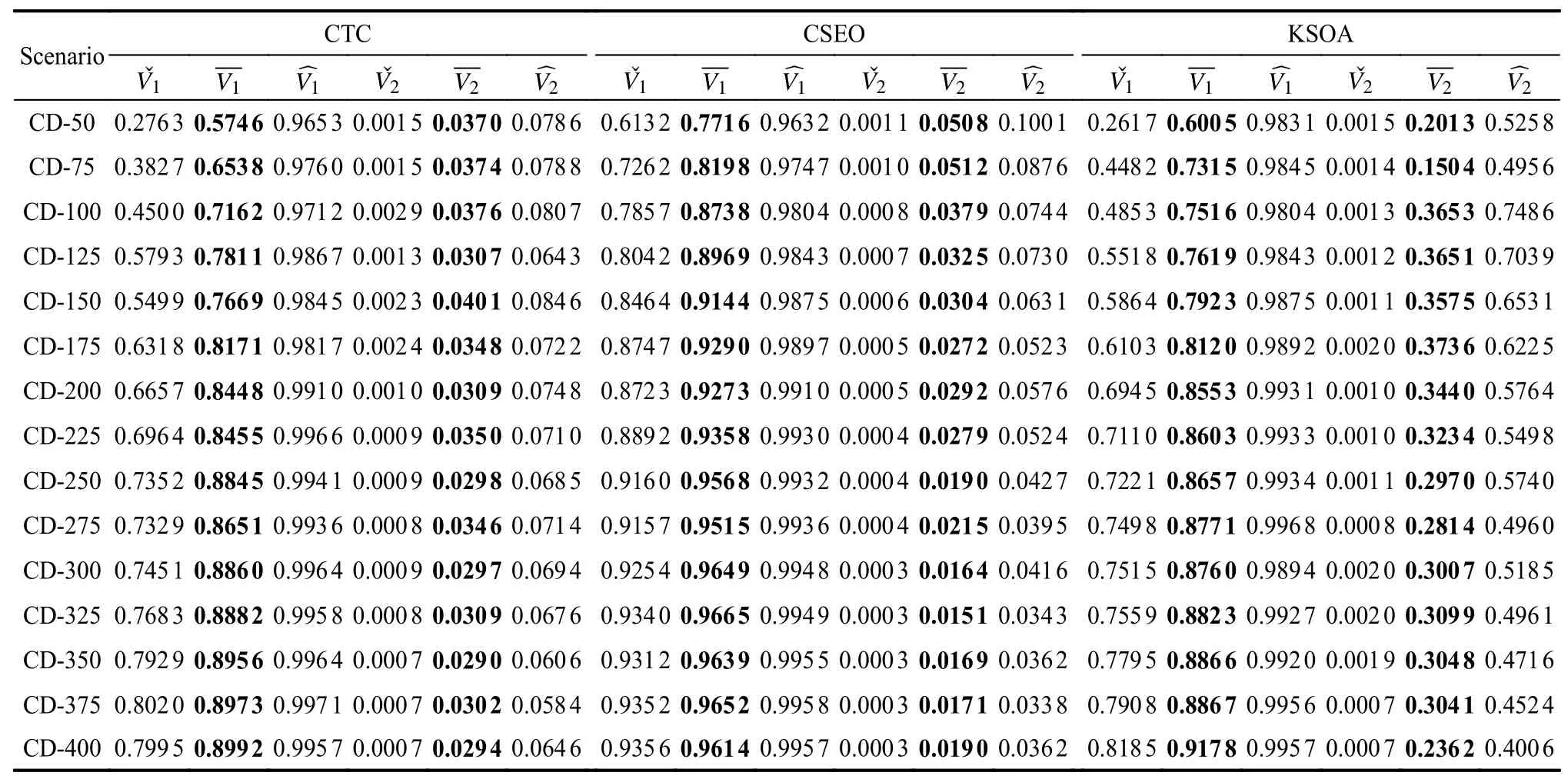
Table 3 Comparing results among CTC,CSEO and KSOA

(i) According to the value of LR,the ground targets scheduled by CSEO are always less than that by CTC and KSOA because of the process of turning on/off the sensor.In CSEO,after observing each ground target,the sensor must be closed.And the process of opening the sensor again will spendTon=180 s,during which the sensor cannot observe any ground target.

(ii) The EC of schemes obtained by KSOA is bigger than that by CTC and CSEO constantly,which is consistent with the analysis in Subsection 2.3 and is also a piece of evidence for explaining the correctness of Definition 2.

(iii) Though the fewer ground targets are observed in schemes obtained by CSEO,the EC of the schemes is not significantly less than that of the scheme obtained by CTC.That phenomenon representing CTC can not only reduce the value of LR,observe more ground targets,but also decrease the value of EC to some extent,which also proves that Definition 1 is reasonable.

(iv) Based on the variation of values of LR and EC,we can find CTC is suitable and necessary for the OSPFAS.

In order to reflect the relationship between schemes obtained by CTC,CSEO and KSOA more intuitively,four scenarios (CD-100,CD-200,CD-300,and CD-400)are chosen as test cases and their Pareto frontiers are drawn in Fig.14.It is significant that the Pareto frontier obtained by ALNS+NSGA-II under CTC is always below that obtained by ALNS+NSGA-II under CSEO and KSOA for all four scenarios.

In addition,the Pareto frontier obtained by ALNS+NSGA-II under CTC is also longer than that obtained by ALNS+NSGA-II under CSEO and KSOA for all four scenarios,which means the diversity of solutions obtained by ALNS+NSGA-II under CTC is most extensive.

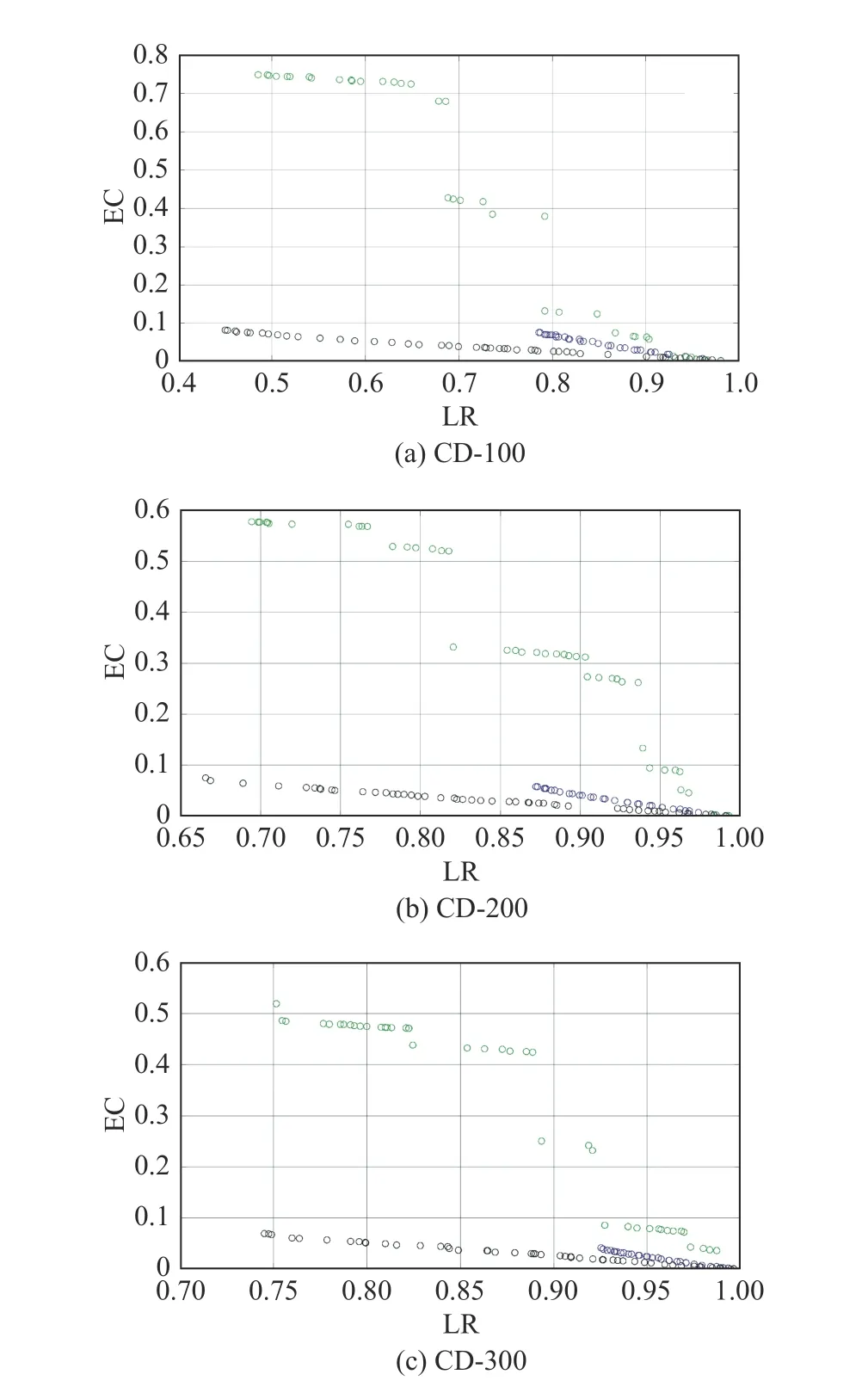
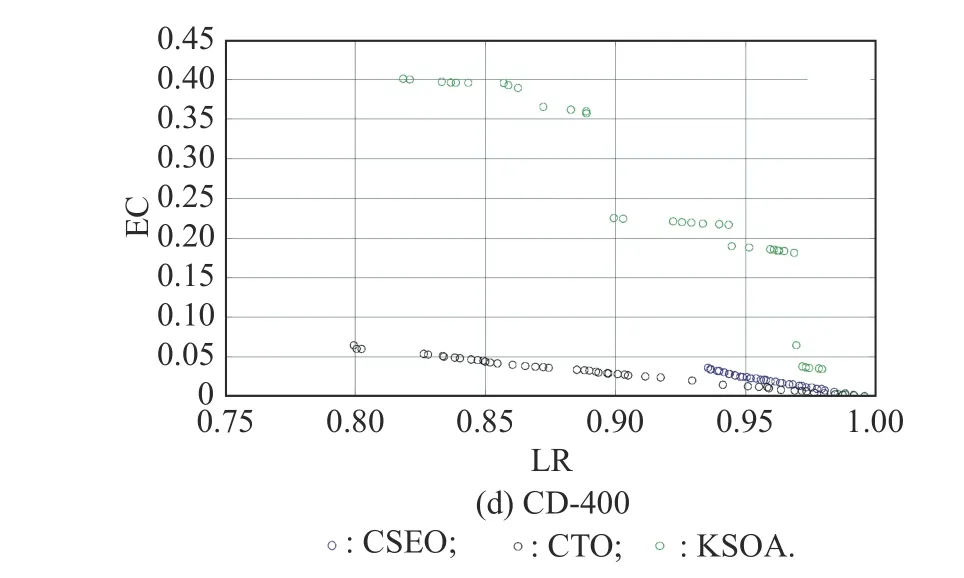
Fig.14 Pareto frontiers for CTC,CSEO and KSOA

6.Conclusions

Considering CTC into the observation scheduling problem for AEOS can improve the efficiency of the AEOS system.Considering the dynamic of CTC,we present a biobjective optimization model to minimize the LR and the EC for describing OSWCTC.With the characteristic of CTC,the ALNS+NSGA-II is designed to solve OSWCTC.RGHA is proposed to construct relatively well initial solutions fast.Two categories operators,“Destroy &Repair”and“Swap”,and/8 operators are designed to improve solutions.A two-stage adaptive layer is built to control updating the weight of every operator and a boxmethod based on the ε-constraint method is adopted to select the offspring solutions fast and avoid decreasing the diversity of solutions.

Extensive simulation experiments based on all the scenarios designed in the study [4]demonstrate the efficiency of our ALNS+NSGA-II algorithm.

(i) According to parameter optimization,we confirm the parameter λ=0.5 which will be good for more operators to contribute to the ALNS+NSGA-II algorithm.

(ii) Comparing with existing algorithms and the control algorithm,our algorithm,ALNS+NSGA-II could obtain the better solutions stably.

(iii) Two control groups,CSEO and KSOA,are proposed to explain the efficiency of CTC.Extensive simulation results reflect that CTC can not only increase the rate of success observation,but also decrease the EC.