Data-driven evolutionary sampling optimization for expensive problems

ZHEN Huixiang ,GONG Wenyin,* ,and WANG Ling

1.School of Computer Science,China University of Geosciences,Wuhan 430074,China;2.Department of Automation,Tsinghua University,Beijing 100084,China

Abstract: Surrogate models have shown to be effective in assisting evolutionary algorithms (EAs) for solving computationally expensive complex optimization problems.However,the effectiveness of the existing surrogate-assisted evolutionary algorithms still needs to be improved.A data-driven evolutionary sampling optimization (DESO) framework is proposed,where at each generation it randomly employs one of two evolutionary sampling strategies,surrogate screening and surrogate local search based on historical data,to effectively balance global and local search.In DESO,the radial basis function (RBF) is used as the surrogate model in the sampling strategy,and different degrees of the evolutionary process are used to sample candidate points.The sampled points by sampling strategies are evaluated,and then added into the database for the updating surrogate model and population in the next sampling.To get the insight of DESO,extensive experiments and analysis of DESO have been performed.The proposed algorithm presents superior computational efficiency and robustness compared with five state-of-the-art algorithms on benchmark problems from 20 to 200 dimensions.Besides,DESO is applied to an airfoil design problem to show its effectiveness.

Keywords:evolutionary algorithm (EA),surrogate model,datadriven,evolutionary sampling,airfoil design.

1.Introduction

Evolutionary algorithms (EAs) or meta-heuristic algorithms (MAs) have become a popular tool for optimization due to their promising global search ability.However,EAs require a large number of function evaluations during the optimization process,which limits their application in many real-world problems [1].In real world,there are many computationally expensive numerical simulations and costly experiments,such as computational fluid dynamics (CFD) [2],computational structural mechanics(CSM) [3],and finite element analysis (FEA) [4].Solving the computationally expensive problems has become popular in science and engineering.Some of them,such as the computation of the objective function and constraints,are extremely expensive,e.g.,single CFD simulation takes from minutes to hours [5].Such expensive function evaluations (FEs) cannot be afforded by EAs,which typically require tens of thousands of FEs to obtain the global optimum.

Surrogate models (also known as meta-models [6])have been widely used in EAs to reduce the computational time.The principle of surrogate-assisted EAs (SAEAs) is that the time cost of surrogate models for predicting the objective function is insignificant compared with expensive function evaluations [7].Jin et al.pointed out that surrogates can be applied to almost all operations of EAs [8],consisting of population initialization,crossover,mutation,local search,fitness evaluation and so on [9−11].A variety of machine learning models have been used to construct surrogates,such as polynomial regression (PR)[12,13],Gaussian processes (GP) [14−16](also known as Kriging [17,18]),radial basis function (RBF) [19],artificial neural networks (ANNs) [20−22],and support vector machine (SVM) [23,24].Moreover,ensemble of surrogates is also used to enhance the performance of SAEAs[25,26].

With limited computational budgets,researchers have conducted detailed studies on ways of employing surrogate models [7,8].The choice of a new sampled point for evaluation is significant for updating the surrogate model and guiding the optimization process.The sampled points,which have good fitness values or high-uncertainty,are promising for fitness evaluation.The sampled points with good fitness values can accelerate the convergence,and the points with high-uncertainty can reduce the risk of falling into local minima.Generally,uncertainty information can be estimated according to the variance provided by the Kriging model [27],the distance to the evaluated sample points [28],and the discrepancies among the predictions of the ensemble surrogates [29].Jones et al.[27]developed the efficient global optimization (EGO) method,where the Kriging model was used to approximate the exact function and the estimated mean square error was used to reflect the prediction variance.Several Krigingbased infill criterions,such as lower confidence bound(LCB) [15],expected improvement (EI) [30],and probability of improvement (PoI) [31],have shown promising performance for low-dimensional optimization problems with fewer than 15 dimensions.However,due to the curse of dimensionality,when dealing with high-dimensional expensive optimization problems,the performance of Kriging-based SAEAs becomes noticeably worse because it is difficult to build an accurate surrogate model in high-dimensional space.On the other hand,RBF-based surrogates are employed widely in high-dimensional expensive optimization [32,33].Kriging and RBF are two widely studied surrogate models.Training of the Kriging model is time-consuming when the number of samples or dimensions is large [34].RBF also is a popular modeling method with high efficiency and accuracy.RBF is more suitable for high-dimensional expensive optimization problems because it works well to approximate high-dimensional nonlinear functions and the training time required for RBF is insensitive to the increase of dimensions.

Various studies indicate that the ability to guide optimization is more worthy of attention than the accuracy of models when facing high-dimensional problems [8,32,33].The surrogate-assisted strategies can be classified into two main categories,surrogate-assisted prescreening and surrogate-assisted local search.Surrogate-assisted prescreening uses the surrogate’s response function to sort the candidate offspring points produced by the basic EAs and then select the points with small predicted responses as the offspring points.Sun et al.used RBF to sort the candidate offspring particles and then screen some potential offspring particles with small response values in the RBF-assisted social learning particle swarm optimization(SLPSO) [35].Li et al.proposed a prescreening criterion based on the prediction difference of multiple surrogates[11].Surrogate-assisted local search is also widely used in SAEAs,which searches promising sample points in the local area based on predicted fitness value by surrogate.Ong et al.employed a trust-region method for the interleaved use of exact models for the objective and constrained functions with computationally cheap RBF surrogates during the local search [36].Wang et al.built a local RBF model for searching one candidate point by the differential evolution (DE) optimizer [32].Cai et al.used the surrogate-based trust region local search method to guide the genetic algorithm to search in an accurate way[34].

Recently,some considerable progress has been made on improving the SAEAs search schemes.Liu et al.presented a Gaussian process surrogate model assisted evolutionary algorithm for medium-scale computationally expensive optimization problems (GPEME) (20-50 decision variables),in which a Gaussian process model with LCB prescreen solutions in a differential evolution algorithm and a dimensional reduction technique was proposed to enhance the accuracy of the GP model [15].Sun et al.proposed a surrogate-assisted cooperative swarm optimization (SA-COSO) algorithm,in which a surrogate-assisted particle swarm optimization (PSO) algorithm and a surrogate-assisted social learning based PSO algorithm cooperatively search for the global optimum [35].Yu et al.proposed a surrogate-assisted hierarchical PSO (SHPSO) algorithm,which builds a local RBF model with a certain number of current best samples [33].On one hand,the optimum of the RBF model is searched as a candidate point by SLPSO.On the other hand,the RBF is used to prescreen out some promising particles whose estimated values are smaller than their personal bests.Wang et al.proposed a novel evolutionary sampling assisted optimization (ESAO) method which consists of two major search strategies,in which a global RBF model is built to choose the best offspring generated by evolutionary operators (mutation and crossover),the other local RBF model is built for searching one candidate point by the DE optimizer,and the two strategies are employed alternately in optimization [32].

In order to improve the effectiveness of the SAEAs.In this paper,we present a data-driven evolutionary sampling optimization (DESO) framework for expensive optimization problems.DESO considers both the surrogate screening (SS) and surrogate local search (SLS) as two different degrees of evolutionary sampling strategies.RBF models are employed as surrogates in the two strategies because of its high accuracy and fast modeling for high dimension problems.SS is used as a global search to find new promising points over the large area.SLS is used to exploit the most promising area.To balance exploration and exploitation and avoid falling into local optima,DESO randomly employs SS or SLS to obtain a new sample point for updating the surrogate model and guiding the optimization process.In each generation,population and surrogate models are updated based on a predefined number of best sample points from database.

The main contributions of the paper are as follows:

(i) Two data-driven evolutionary sampling strategies,SS based on evolutionary operators and SLS based on the evolutionary optimizer,are proposed to sample promising points.They are used for the global search and local search,respectively.

(ii) The proposed method uses one of the two evolutionary sampling strategies randomly in each iteration to balance exploration and exploitation.Moreover,adaptive parameters are set for different dimensional problems.

(iii) The proposed method shows superiority compared to five state-of-the-art algorithms on 30 test functions and an airfoil design problem.

The remainder of this paper is organized as follows.Section 2 introduces the related techniques,such as DE and RBF networks.Section 3 details the data-driven evolutionary sampling optimization framework.Subsequently,experimental results and analysis are conducted in Section 4.Finally,Section 5 concludes this paper and discusses the possible future work.

2.Related techniques

2.1 DE

DE,proposed by Storn and Price [37],is a very popular EA,which contains four main operations:initialization,mutation,crossover,and selection.DE is widely used in various scientific and engineering optimization problems[38].Researchers have proposed different variants of the basic algorithm to improve its performance [39−41].In this work,DE is employed as the optimizer for SLS,and its mutation and crossover operations are also used to generate sample points for SS.

Suppose that a population withnindividuals is expressed asP=[x1,x2,···,xn].Theith individual withddimensions isinP.The mutation and crossover are briefly introduced as follows.

In mutation,the mutant vector can be obtained by the mutation operator.The commonly used mutation operators are as follows.

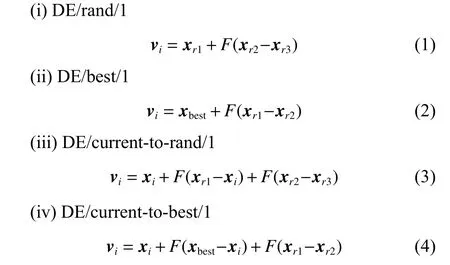
wherexr1,xr2,andxr3are three mutually different individuals chosen from the current population,andFis a scaling factor which typically lies in the interval [0.4,1].DE/rand/1 is selected in this work.

In crossover,the trial vector,expressed asui=is generated fromxiandvi.There are two kinds of crossover methods:exponential and binomial method.In this work,we just introduce the binomial,whose formula can be expressed as

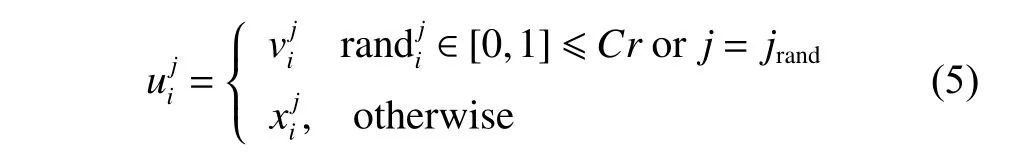
2.2 RBF network

RBF is widely used as the surrogate model for high-dimensional expensive problems (n>30) [34].Given the sampled pointsRBF uses a weighted sum of basis-functions to approximate the fitness function landscape as follows:

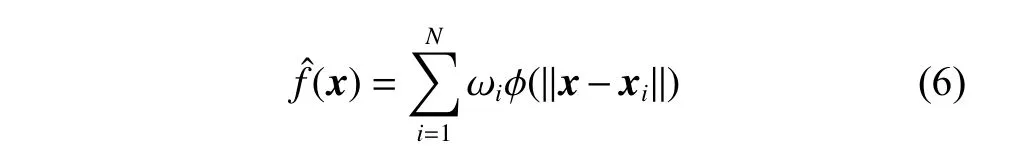
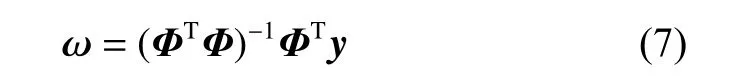
wherey=[y1,y2,···,yN]Ti s the output vector and Φ is the following matrix:

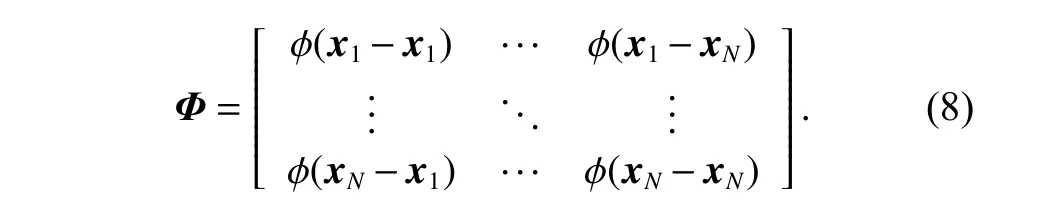
The shape parameter of the Gaussian kernel function,referred to [33],is set toβ=Dmax(dN)−1/d,whereDmaxis the maximal distance between the training data.Once parameterβand the training samples are obtained,the RBF model can be constructed efficiently.

3.DESO

In this section,DESO is proposed,which consists of two evolutionary sampling strategies:SS for global search and SLS for surrogate local search.They can be seen as sampling methods with different evolutionary degrees,because SS contains once evolutionary operators and SLS finds one candidate by the whole evolution optimization process.DESO attaches importance to historical sample points very much.In each generation,evolutionary sampling strategies obtain a sample point for evaluation,then the evaluated sample point is added to the database,until the budget of fitness evaluation uses up.Sample points with good performance guide DESO to search promising areas by building RBF models and constituting population.In this paper,the evolutionary sampling process employs randomly one of the two sampling strategies,SS based on the evolutionary operators and SLS based on the evolutionary optimizer,to balance exploration and exploitation.

Algorithm 1Pseudo code of the proposed DESO.

3.1 SS based on evolutionary operators

The pseudo code of SS based on evolutionary operators is shown in lines 7 to 11 of Algorithm 1.The strategy selects the bestNsamples in database to form population,and build an RBF modelusing the bestmsamples.In early optimization,all sample points in the database are used to train the RBF model.When the database is big enough,we setmto a fixed value avoiding too much training time.In this work,we set a maximum ofmto 300.Then,the population generates the same number of offspring by evolutionary operators.Different EAs operators can be used here,such as DE,PSO,and GA.We employ DE/rand/1 mutation and crossover.The candidate pointxcwith the lowest prediction value will be evaluated by using the expensive fitness function.Finally,the evaluated sample point is added into the database.When the evaluated sample point is better than the worst of the sample in population,the new sample will be selected to form population and then helps guide the optimization process.

3.2 SLS based on evolutionary optimizer

The surrogate local search strategy aims to find the optimum of the local surrogate model to accelerate the convergence of the optimization process.The pseudo code can be seen in lines 13 to 16 of Algorithm 1.SLS firstly selectsτbest samples from the database as a sample setsfor local search.The local surrogate model is built by training the RBF model with theτsample points.Different from the SS strategy,the SLS strategy builds a surrogate model using a small number of sample points.Moreover,in order to solve problems of different dimensions,τis set to 25+dand its maximum is 60,wheredis the dimension of the problem.Search area [l,u]is also determined by the sample set referring to (9) and (10).For each variable,we set the upper bound and the lower bound of the sample set as search ranges of the local search.

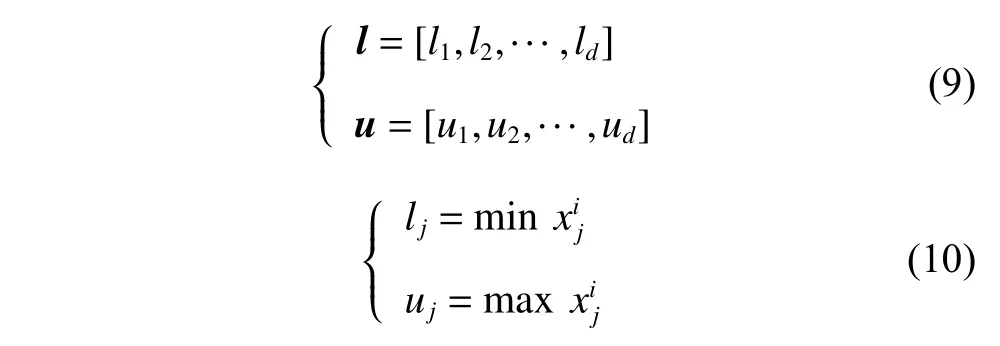
wherei=1,2,···,τ.

Then the evolutionary optimizer can search one candidate sample point by minimizingunder preset stopping criteria.It should be noted that the stop criterion of the optimizer does not need to be set very strict since the surrogate model has error.The evolutionary optimizer can be DE,PSO,and GA.For researching the performance of evolutionary optimizers,we will test different evolutionary optimizers in Section 4.After fitness evaluation,the new sample point is added into the database.Same as the surrogate screening strategy,the new sample point with good performance will help for building RBF models and updating search area [l,u]in the next generation.

3.3 Framework of the proposed DESO

The proposed DESO method combines the global search and the local search to balance exploration and exploitation.They are realized by two different types of evolutionary sampling strategies.

The framework of DESO is shown in Fig.1.The solid arrows stand for the flows of the algorithm,and the dotted arrows represent the data flow.The pseudo code of DESO is shown in Algorithm 1.Initially,N0sample points are generated from the design space by using Latin hypercube sampling (LHS) [47],which segments the distribution intonintervals and makes sure that at least one value is randomly selected form each interval.The number of intervals,n,is the number of iterations of LHS.Then,the fitness value of samples is evaluated,and the database is generated.DatabaseDconsists of all evaluated sample points.Before evolutionary sampling,Dis sorted asDsortaccording to the fittness value.Evolutionary sampling is used to find the promising sample point for fitness evaluation.In this phase,DESO randomly selects a strategy between SS and SLS in each iteration until the termination condition is met.Through this way,evolutionary sampling effectively accelerates the convergence and avoids falling into the local optimum.If SS is employed,Nbest sample points are used to form the population.All sample points are used to build the global RBF model.As the number of training sample points increases,the process of the training surrogate model becomes time-consuming.Thus when the number of sample points is large enough (more thanm),the global RBF model is built by usingmbest sample points.If the SLS strategy is employed,τbest sample points are used to build the local RBF model.And the search space is set based on theτbest sample points.SS plays the role of exploration and SLS plays the role of exploitation.

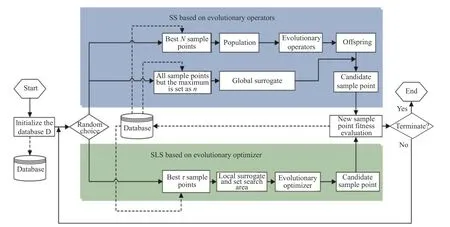
Fig.1 A diagram of the proposed framework

4.Experimental study and discussion

The algorithm considers the characteristics of high-dimensional problems,and set adaptive parameters in SLS for different dimensions.Therefore,it can solve the problems with different dimensions.In this section,we set up 30 test functions including six types of test questions and five different dimensions,as shown in Table 1.Table 2 shows the result of DESO on 30 test functions.For convenience,we use simplified names for easy understanding of a specific problem.For example,G20 represents the 20-dimensional Griewank problem,and SRR100 represents the 100-dimensional shifted rotated rastrigin problem.Moreover,we take the discussion and experimental study of DESO.On one hand,we discuss the effect of sampling strategies (SS and SLS) on DESO.On the other hand,we research the impact of the evolutionary optimizer on SLS by testing different optimizers.Finally,we compare the proposed DESO algorithm with five stateof-the-art algorithms.All test problems are limited in 1 000 function evaluations,and 20 independent runs are performed to obtain statistical results.

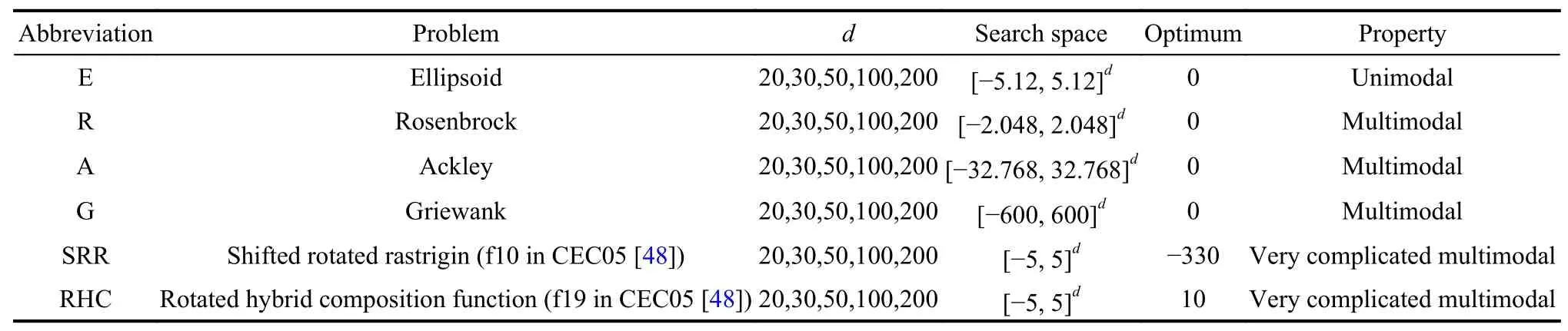
Table 1 Properties of the test problems

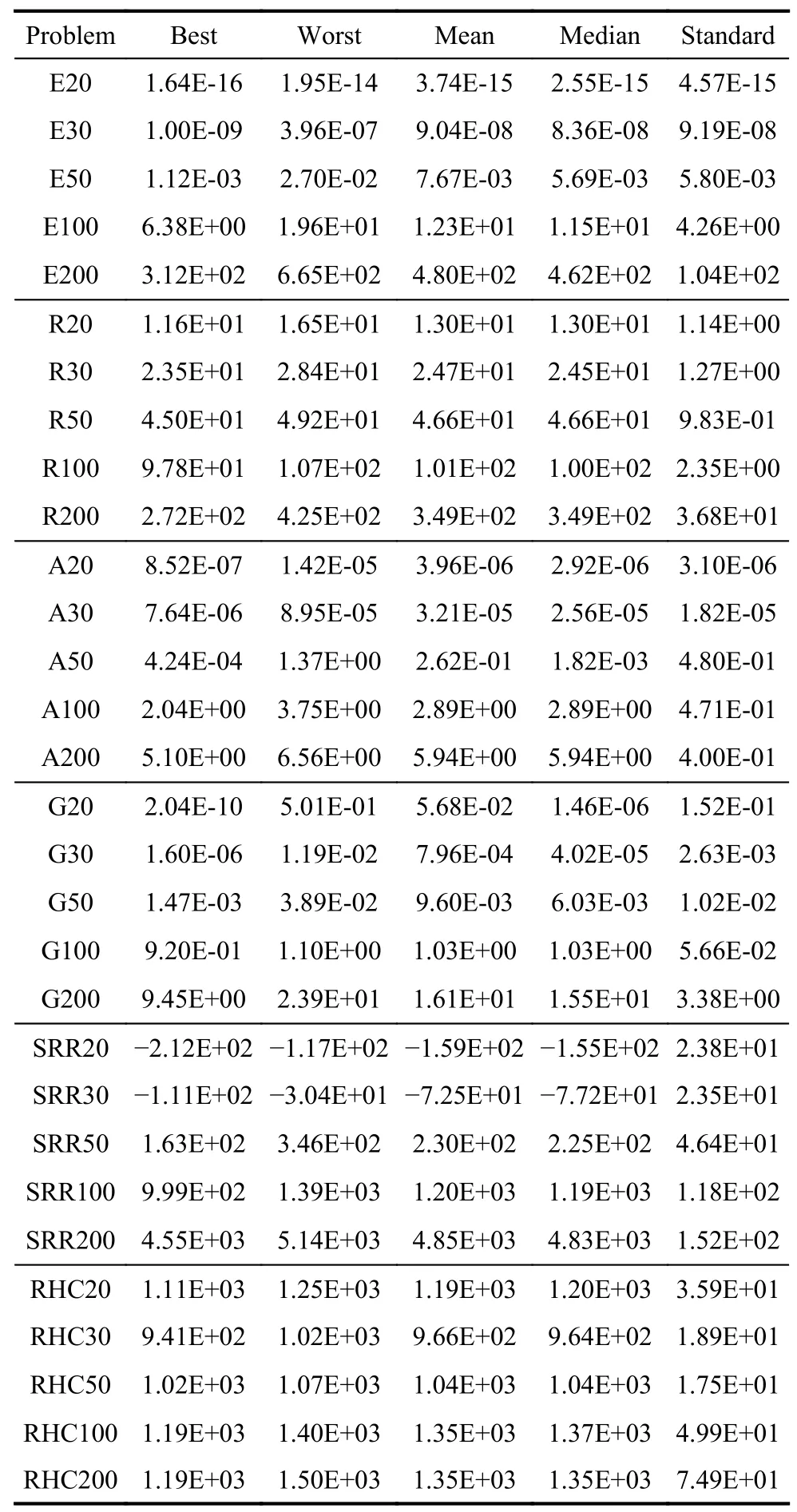
Table 2 Statistical results of 30 test problems obtained by DESO

4.1 Parameter settings

The proposed DESO framework is flexible to implement a specific algorithm.Parameters are set in this paper as follows.Initially,N0sample points are generated by LHS,then the fitness value is evaluated.N0is set to 100 when the dimension is less than 100,otherwiseN0is 200.Database contains all sample points evaluated by the original objective function.In the SS strategy,we setNto 50 andmto the number of samples in the database,but limit the maximum value ofmto 300 [33].In the SLS strategy,in order to adapt to problems with different dimensions,τis set to 25+d,and the maximum ofτis set to 60,wheredrepresents the dimension of the problem.The evolutionary operators of DE are used in the two strategies,andFandCrare set to 0.5 and 0.9,respectively.In SLS,when using the evolutionary optimizer to search for candidate solution,the termination condition of the optimizer is that the number of surrogate model evaluations reaches 1 000+100dor the optimizer does not find better predictions for 10 consecutive generations.

4.2 Discussions

4.2.1 Discussion on sampling strategy

The key of DESO is the data-driven evolutionary sampling strategy.In order to verify effectiveness of the evolutionary sampling process in this paper,we compare DESO with its two variants that only use SS or SLS in the evolutionary sampling process,which are referred to here as DESO-SS and DESO-SLS.It can be seen from Figs.2−5 that DESO-SS has a slower convergence rate comparing with DESO and DESO-SLS,where NFE stands for the number of fitness evaluation.The reason is that the SS strategy prefers exploration rather than exploitation.On the contrary,DESO-SLS initially converges faster than DESO.However,because the SLS strategy only focuses on local exploitation,it is easy to fall into local optimum in the search process.Randomly employing the SLS strategy and the SS strategy can balance the two capabilities of exploration and exploitation,and improve robustness of the algorithm.

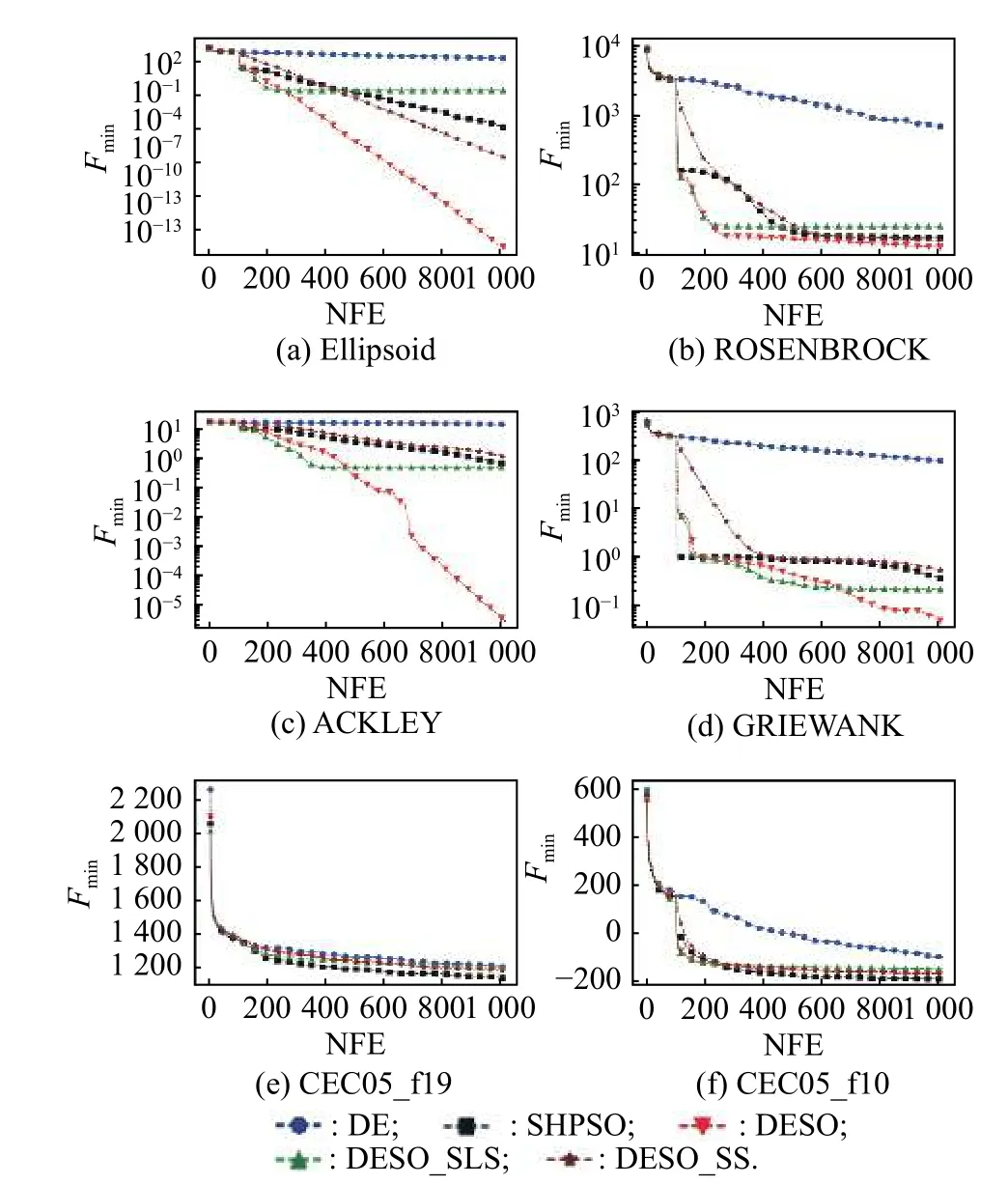
Fig.2 Convergence curves of different algorithms for the 20D benchmark problems

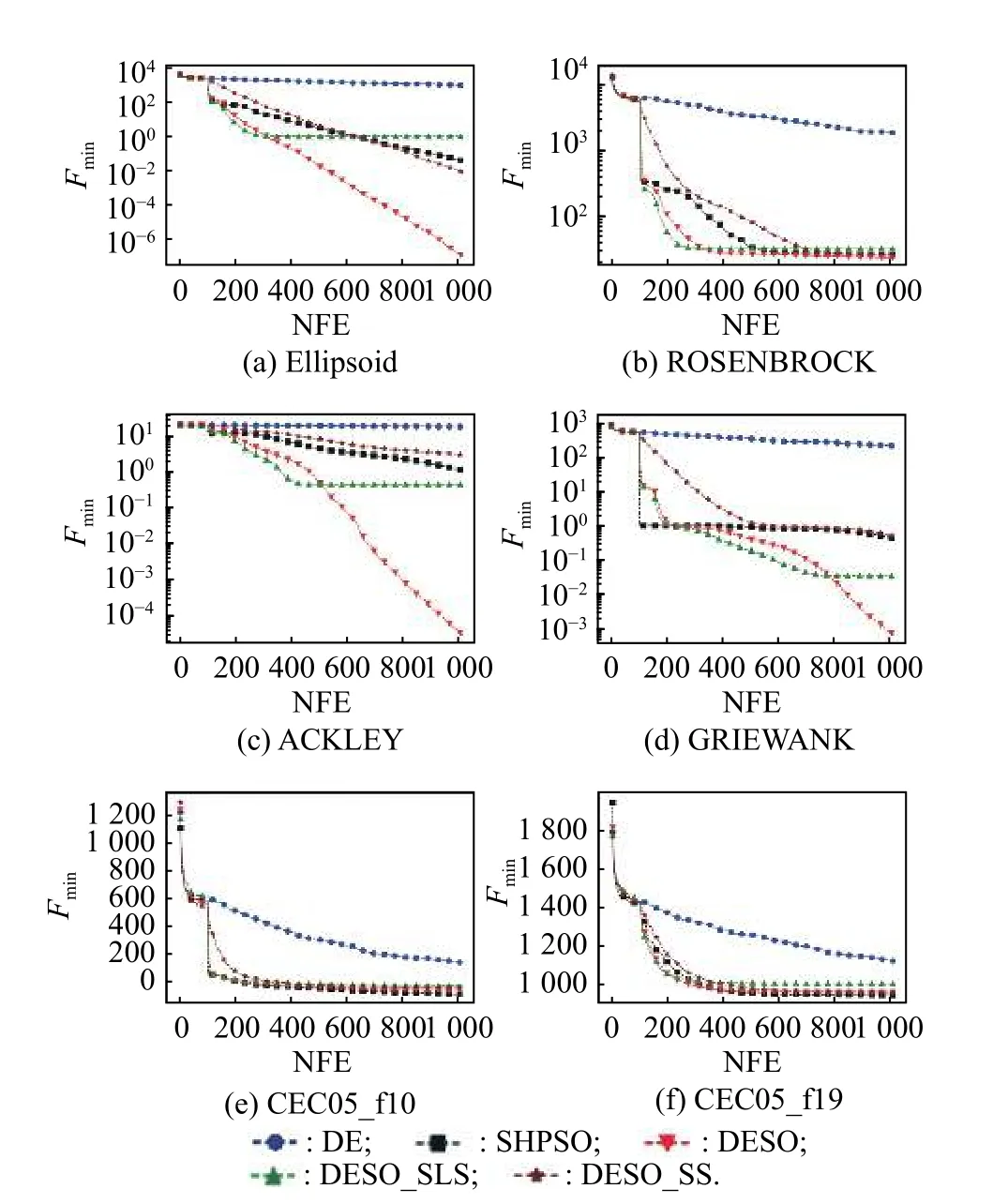
Fig.3 Convergence curves of different algorithms for the 30D benchmark problems

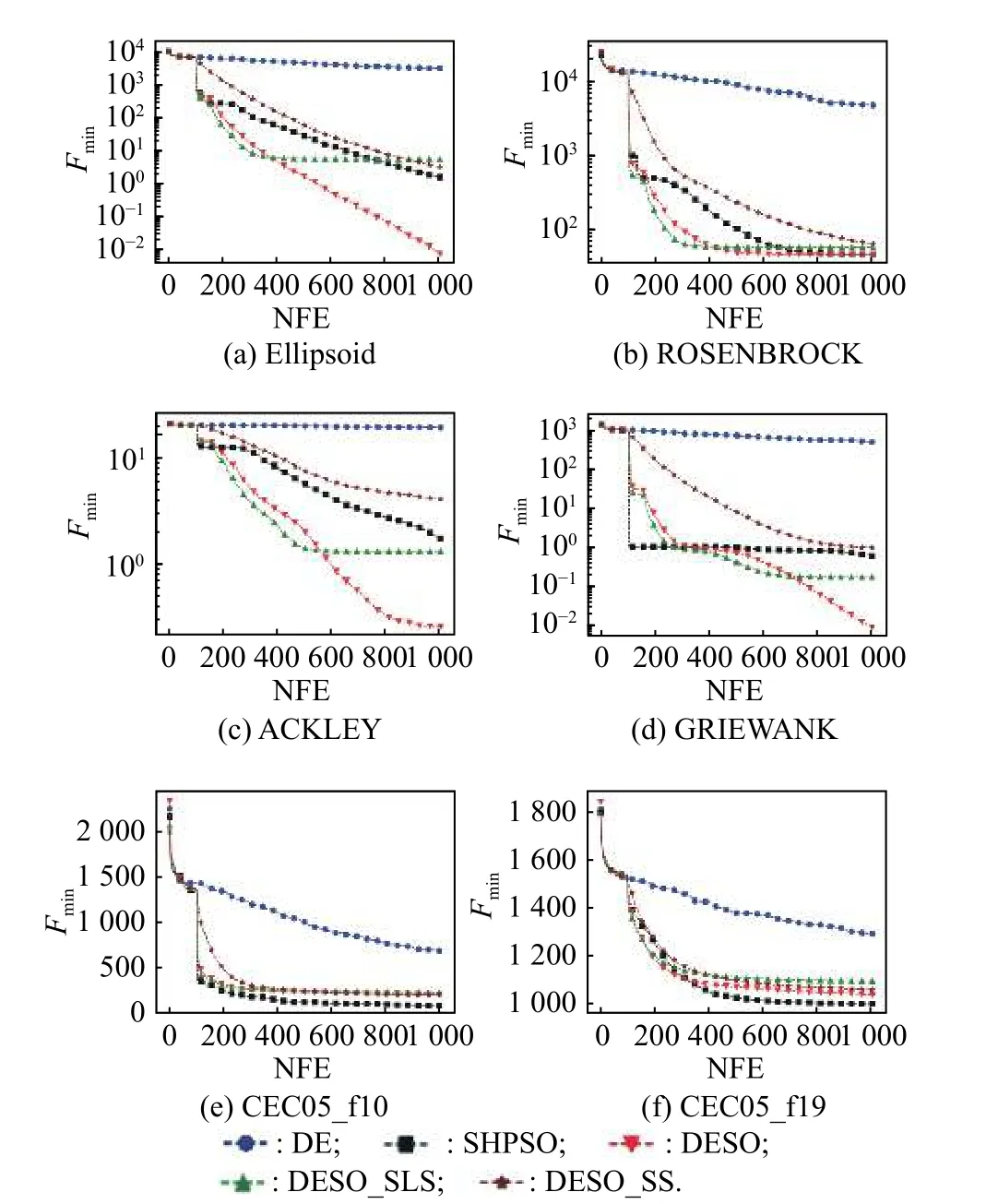
Fig.4 Convergence curves of different algorithms for the 50D benchmark problems

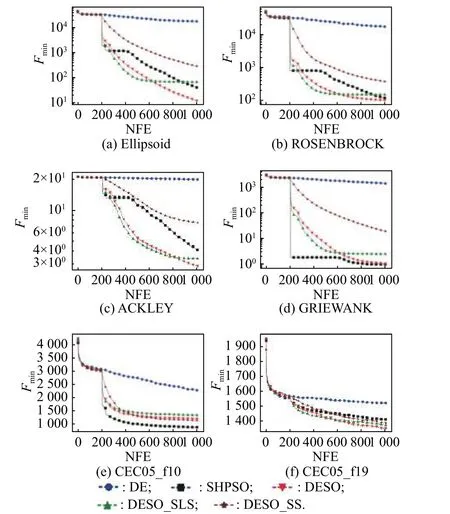
Fig.5 Convergence curves of different algorithms for the 100D benchmark problems

As shown in Table 3,DESO is significantly better than DESO-SS and DESO-SLS in Ellipsoid,Rosenbrock,Ackley,and Griewank problems,but for SRR and RHC,which are very complicated multimodal problems,their effects are not much different.Even for SRR50,SRR100 and RHC20,DESO-SS is slightly better than DESO.

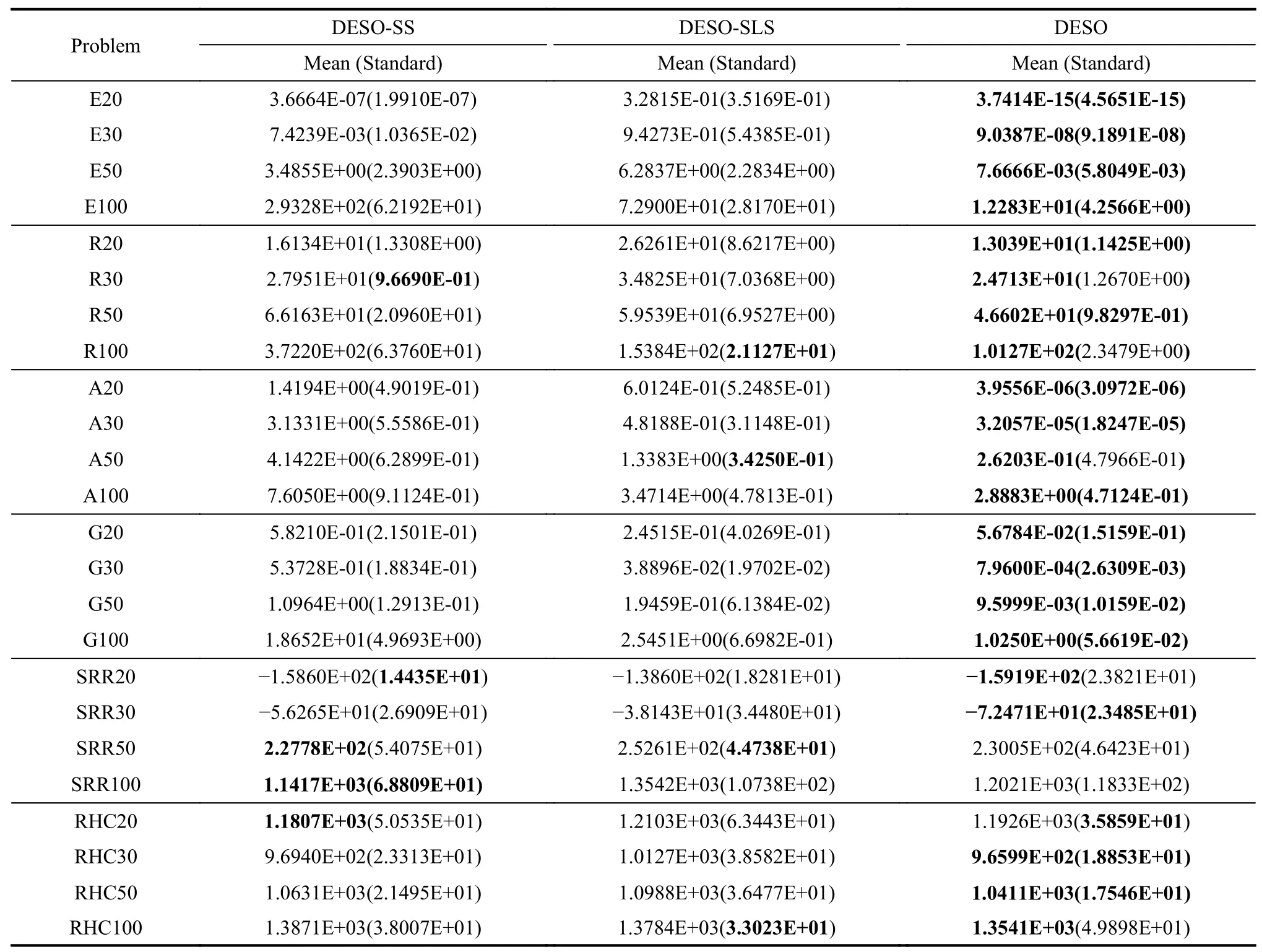
Table 3 Comparison of DESO using different sampling strategies

4.2.2 Discussion on SLS with different optimizers

We consider whether the optimizer used in the SLS strategy will have a great impact on DESO performance.Then we compare three variants of DESO,DESO-PSO using the PSO algorithm as the optimizer,DESO-JADE using the JADE algorithm as the optimizer and DESODE using the DE algorithm as the optimizer (that is,the DESO algorithm introduced in this article).The results can be seen in Table 4.It shows that their results have not much difference.Different optimizers in SLS just have slight import to the performance of DESO when the used optimizers are effective.The reason may be that the SLS strategy searches on the surrogate model.The candidate solution depends heavily on the accuracy of the surrogate model.In high-dimensional problems,it is difficult to guarantee a promising candidate solution on the surrogate model also performs well on the original objective function.Hence,improving the accuracy of the surrogate model is a more important issue than the optimizer.

4.3 Comparison with other methods

As seen in Table 2,DESO performs very well on the Ellipsoid,Rosenbrock,Ackley,and Griewank problems.The median of E20-E50,A20-A50,and G20-G50 can all reach the order of 103,and it can be considered that a suitable optimal solution has been found.Due to the inherent characteristics of the Rosenblock function,the late convergence is very slow.SRR and RHC problems are very complicated.It is not easy for DESO to find the basin of attraction of the global minimum,then exert its efficient exploitation capability.For the same type of problem,the evaluation value of the low-dimensional problem is smaller than that of the high-dimensional problem,but G20 is an exception.According to Locatelli’s research[49],the reason is that the effect of the production of cosine components (the second term of Griewank function)can be neglected as the dimension increases.In addition,compared with A30,the difference between the best solution of A50 and the worst solution of A50 suddenly becomes larger.Because as the dimension increases,it becomes difficult to quickly find the global optimal solution.In A50,sometimes the global optimal region can be quickly found by exploration,but sometimes it cannot.The same problem also occurs on the G20.

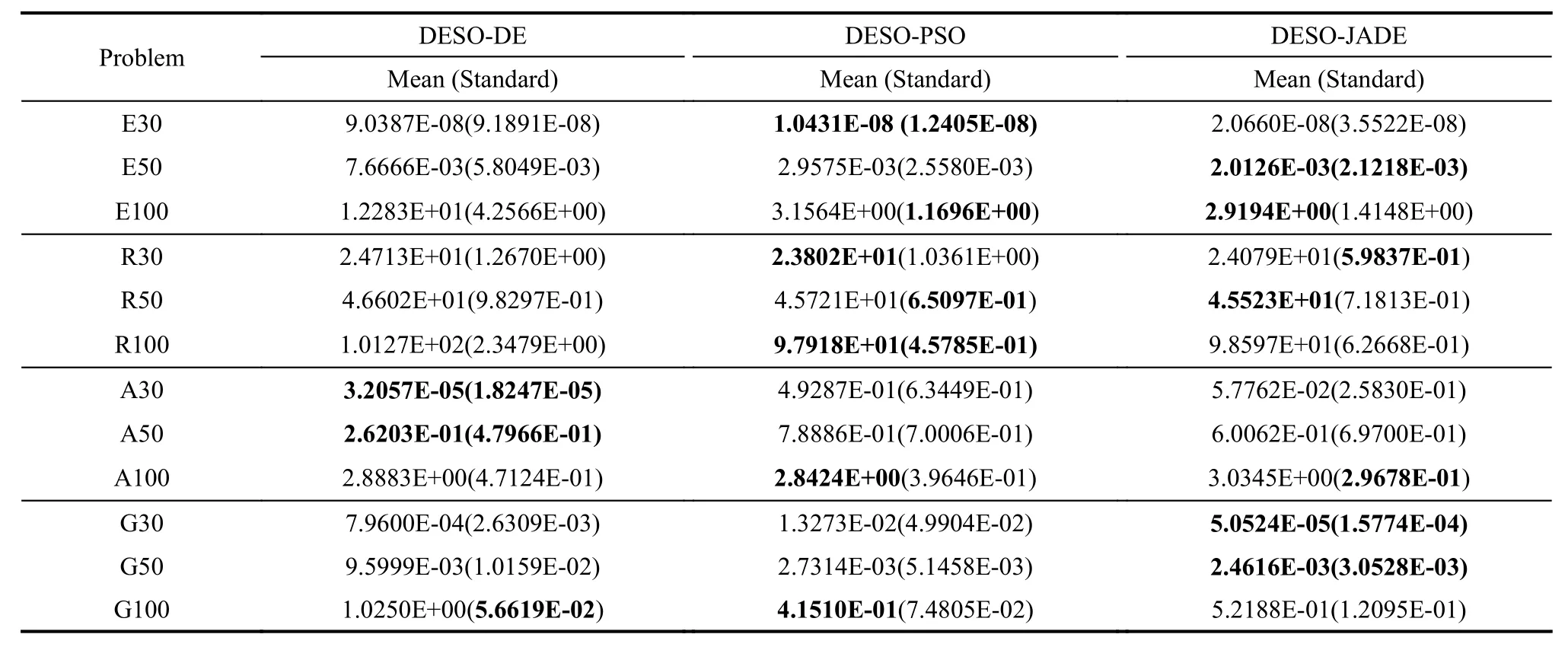
Table 4 Comparison of DESO using different local search optimizers

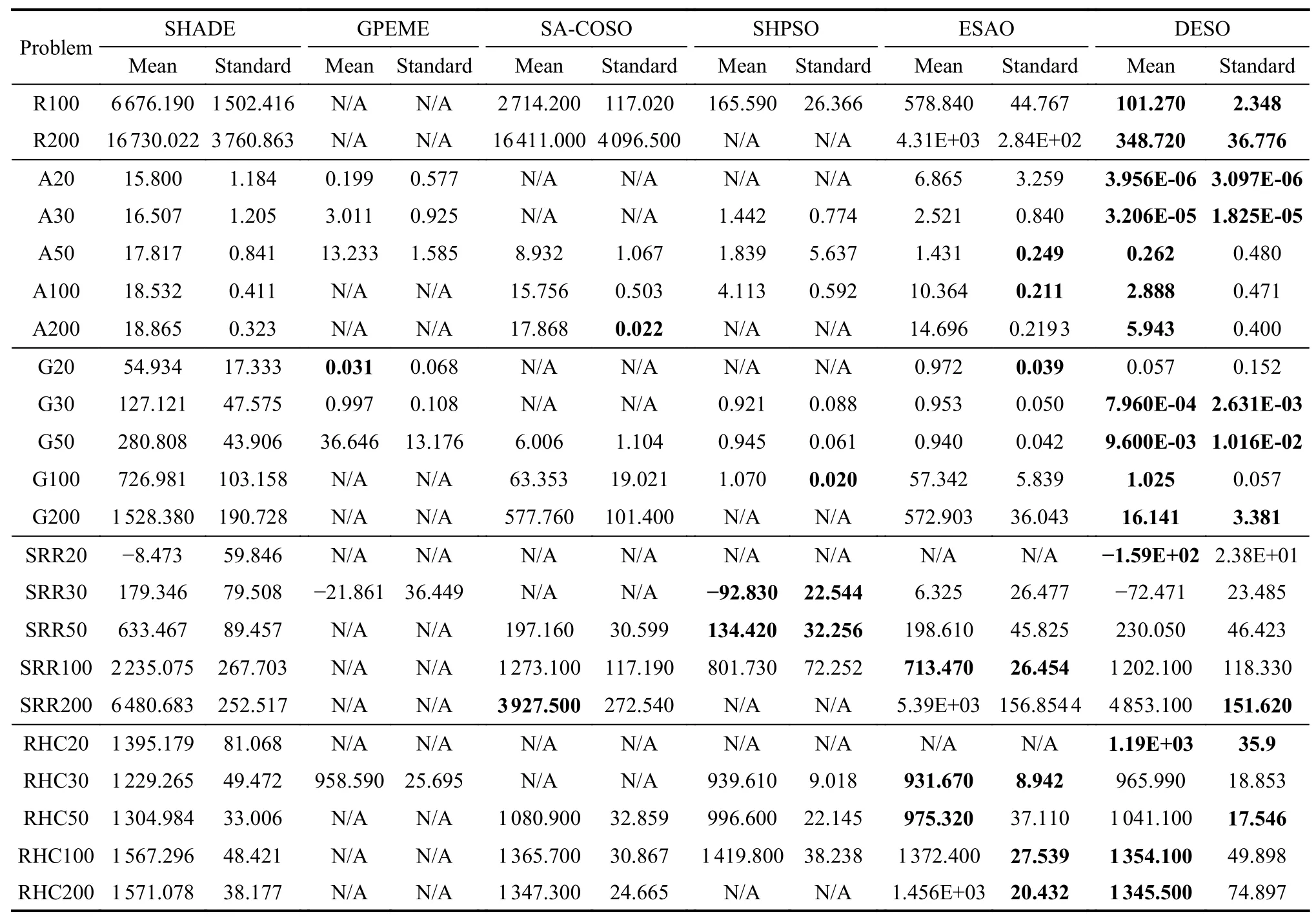
Fig.2 to Fig.5 respectively show the convergence process of DESO in the 20-dimensional to 100-dimensional problems,where thex-axis is NFE and they-axis is the average current fitness value.Compared with the DE algorithm,DESO significantly accelerates the convergence speed.With only 1 000 function evaluations,DESO can obtain an appropriate solution.We compare the DESO algorithm with success-history based adaptive DE(SHADE) [50],an excellent variant of DE,and four stateof-the-art SAEA algorithms,such as GPEME [15],SACOSO [35],SHPSO [33]and ESAO [32].Compared with the five algorithms,DESO has obvious advantages to different dimensions of the Ellipsoid,Rosenbrock,Ackley,and Griewank problems.DESO converges faster and has a higher accuracy.The comparison results of DESO and the five algorithms can be seen in Table 5.In this table,results of GPEME,SA-COSO,SHPSO and ESAO refer to their origin literature.N/A means there is no result of the test function in literature.The best results of test functions are bold.DESO significantly outperforms the SHADE on all benchmark functions.It shows that SAEA is better than traditional EA in expensive problems.For different dimensional Ellipsoid,Rosenbrock,Ackley,and Griewank problems,DESO is significantly better than GPEME,SA-COSO,SHPSO,and ESAO.The result demonstrates DESO has powerful search capabilities.For SRR and RHC problems,the performance of DESO is not much different from GPEME,ESAO and SA-COSO,and worse than SHPSO.

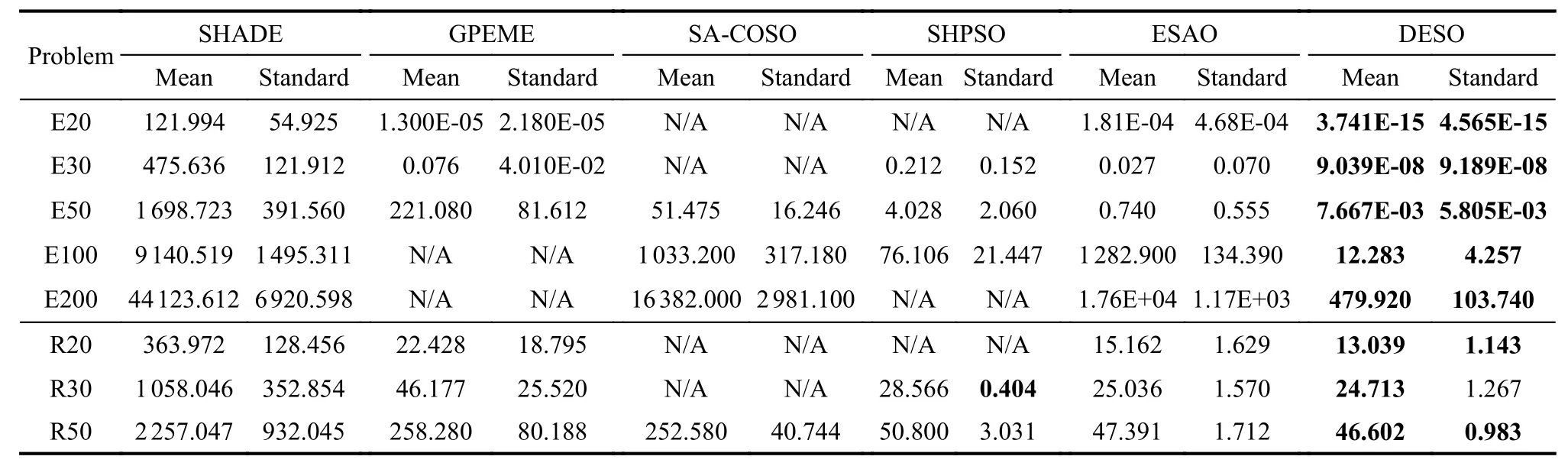
Table 5 Comparison of DESO with other algorithms

Continued

4.4 Application of DESO in an airfoil design problem

After DESO has shown its effectiveness on benchmark problems,we apply it to an airfoil design problem.The airfoil geometry is parameterized by the parametric section method (PARSEC) geometry representation method[51]in this work.Design variables for PARSEC are shown in Fig.6.The optimization problem includes 11 variables.We have chosen the NACA2411 airfoil as the baseline because it is considered to be a good demonstrator for low subsonic flows [52].The design values of the initial airfoil and search range are provided in Table 6.As the original value ispand the search range isr,the search area is [p−r,p+r].We employ an objective function that solves the coefficient of lift of an airfoil using the Vortex panel method given input parameters.The goal of the optimization problem is to obtain the maximum lift coefficient through searching PARSEC parameters.To compare the algorithm with ESAO,SHPSO,and DE,we set the same parameters in experiment.The initial sample points number is 50.The population size is set to 30.The budget of fitness evaluations is 500.For each algorithm,20 independent runs are carried out and the statistical results are given.Table 7 shows the statistical results of the airfoil problem using DESO,ESAO,SHPSO,and DE.DESO performs the best on all the criteria.ESAO and SHPSO obtain some worse designs,and they hold almost the same performance.DE performs the worst.Fig.7 shows the best optimized geometries of the airfoil by the four algorithms.The results of DESO,ESAO and SHPSO are basically in the same shape.The shape of DE is slightly different from them.Fig.8 shows the original shape and the DESO optimized shape.The optimized shape has obvious changes.In addition,the convergence history of the airfoil problem using four algorithms is showed in Fig.9.The result shows DESO performs the best over the whole optimization process.Especially,when the fitness evaluation is less,for example,150 or 300,DESO outperforms other algorithms.

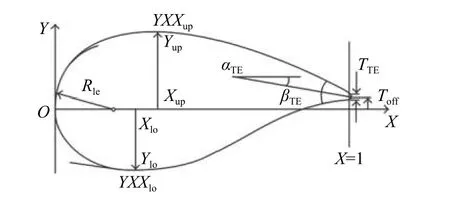
Fig.6 Design variables for PARSEC

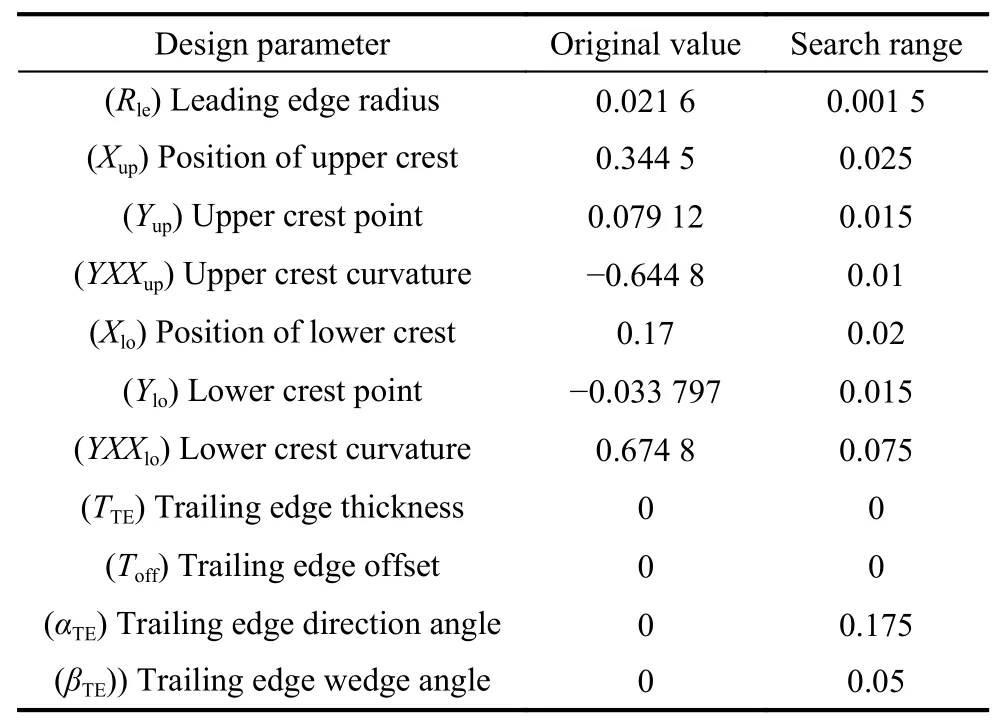
Table 6 Optimized PARSEC parameters

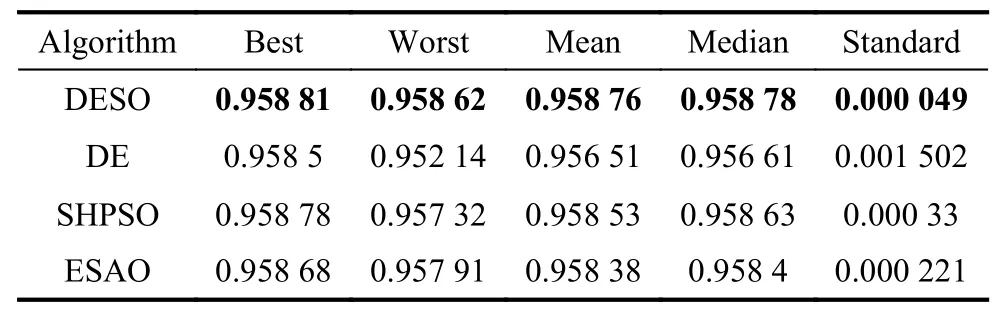
Table 7 Results of comparison

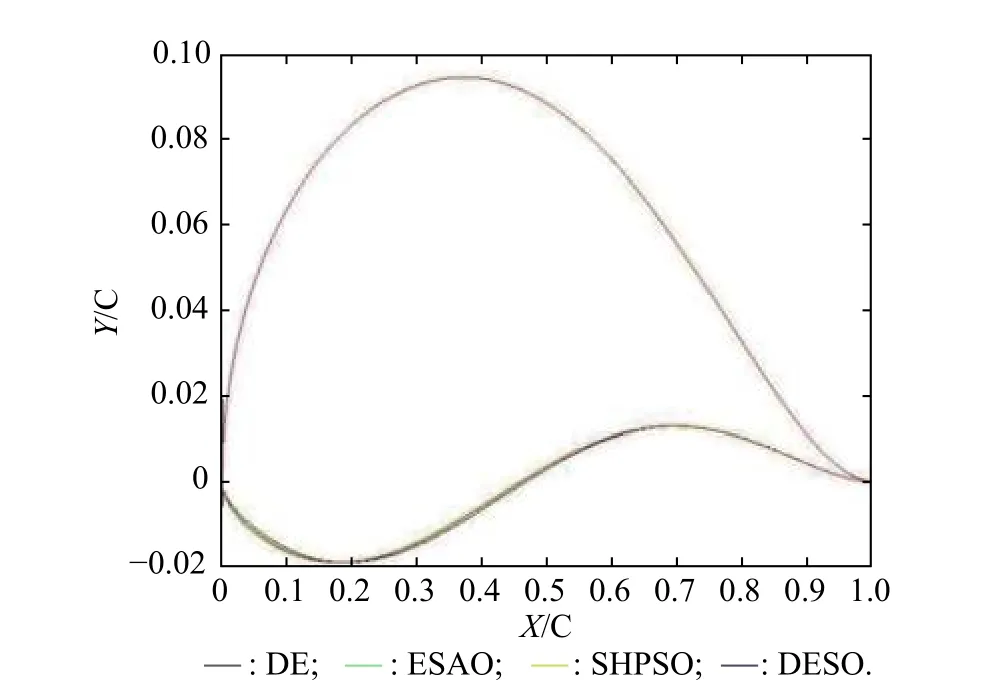
Fig.7 Geometry of the best optimized airfoils of four algorithms

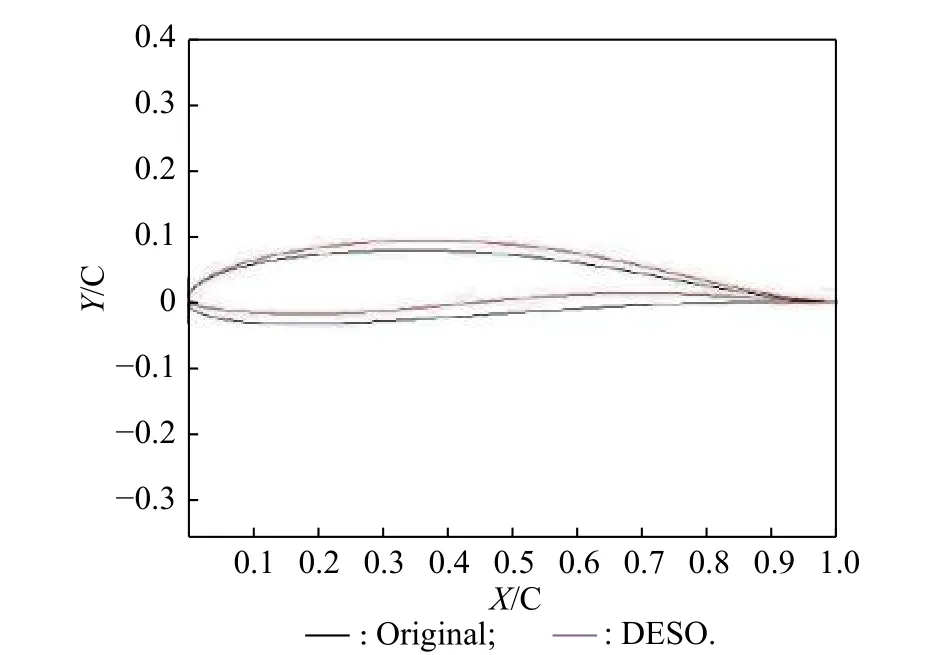
Fig.8 Geometry of the initial and the best optimized airfoils of DESO

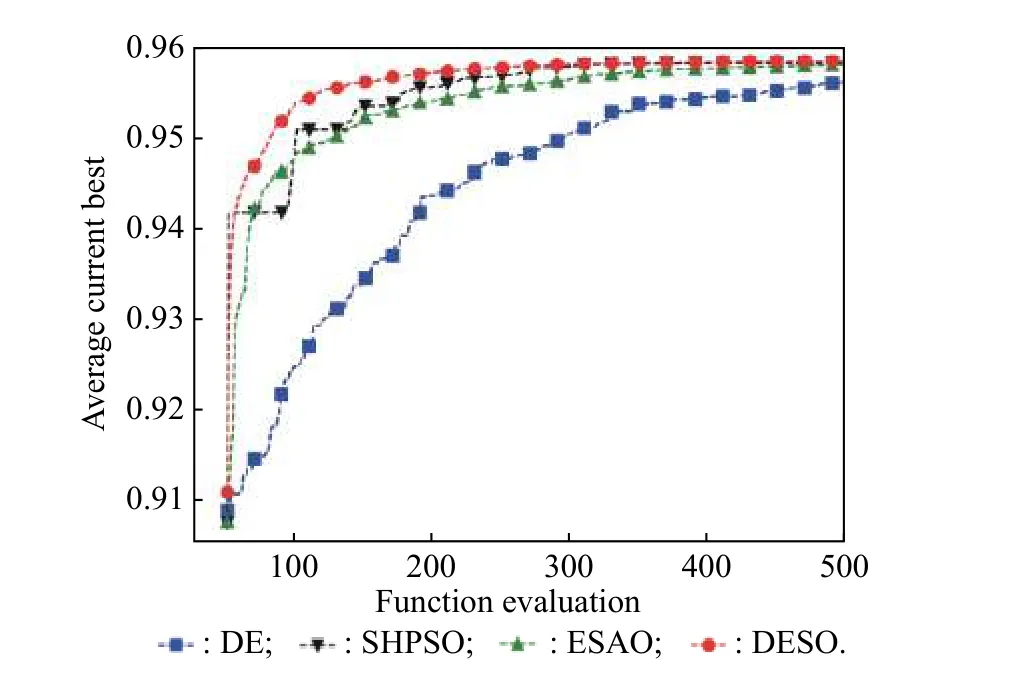
Fig.9 Convergence history of the airfoil problem using four algorithms

5.Conclusions

To solve the expensive optimization problems,this paper proposes a DESO framework,which combines two different degrees of evolutionary sampling strategies,SS and SLS.These two sampling strategies use the historical data to construct global surrogate and local surrogate to assist sampling,respectively.Moreover,DESO sets adaptive parameters for different dimension problems.Experiments with different sampling strategies show that randomly employing two sampling strategies can balance global search and local search and avoid falling into the local optimum.The proposed algorithm is compared with five state-of-the-art algorithms on six widely used benchmark problems of different dimensions ranging from 20 to 200.The results indicate that DESO is effective and efficient.Finally,an application of the airfoil design problem also shows the superiority of DESO.In the future,more efficient sampling strategies need be studied for higher-dimensional problems.Moreover,DESO works well to accelerate the convergence,but its exploration ability should be further improved when handling very complicated problems.