基于电位滴定法测定混凝土中氯离子含量的研究

王志慧

（交通运输部 天津水运工程科学研究所，天津300456）

建筑行业不断发展的同时也促进了钢筋混凝土的推广应用。针对混凝土自身来讲，氯化物是一种极具破坏性的侵蚀物质，它会破坏混凝土的保护层，导致混凝土制件体积膨胀，进而破坏整个混凝土的结构[1]。研究Cl-含量测定方法可以保证测定方法的准确性，解决钢筋混凝土结构不耐受的问题，提高混凝土构件的使用寿命[2]。同时，也能够帮助科研人员研究氯盐的破坏机理，为测定方法提供新的思路。传统的混凝土中Cl-含量测定方法，如文献[3]中的利用速测条法的Cl-含量测定方法、文献[4]的结合耦合多相传输的Cl-含量测定方法在实际运用时存在误差，难以准确得到计算出混凝土内Cl-的含量，为此研究一种基于电位滴定法的混凝土中Cl-含量测定方法，帮助解决传统测定方法的不足。

1 测定研究

1.1 测定准备

除准备所需的电位滴定仪外，由于Cl-含量测定结果的准确性对混凝土工程质量及结构耐久性评定具有重要影响。因此，实验准备6#胸墙部分的混凝土作为实验构件，其详细的相关参数见表1。

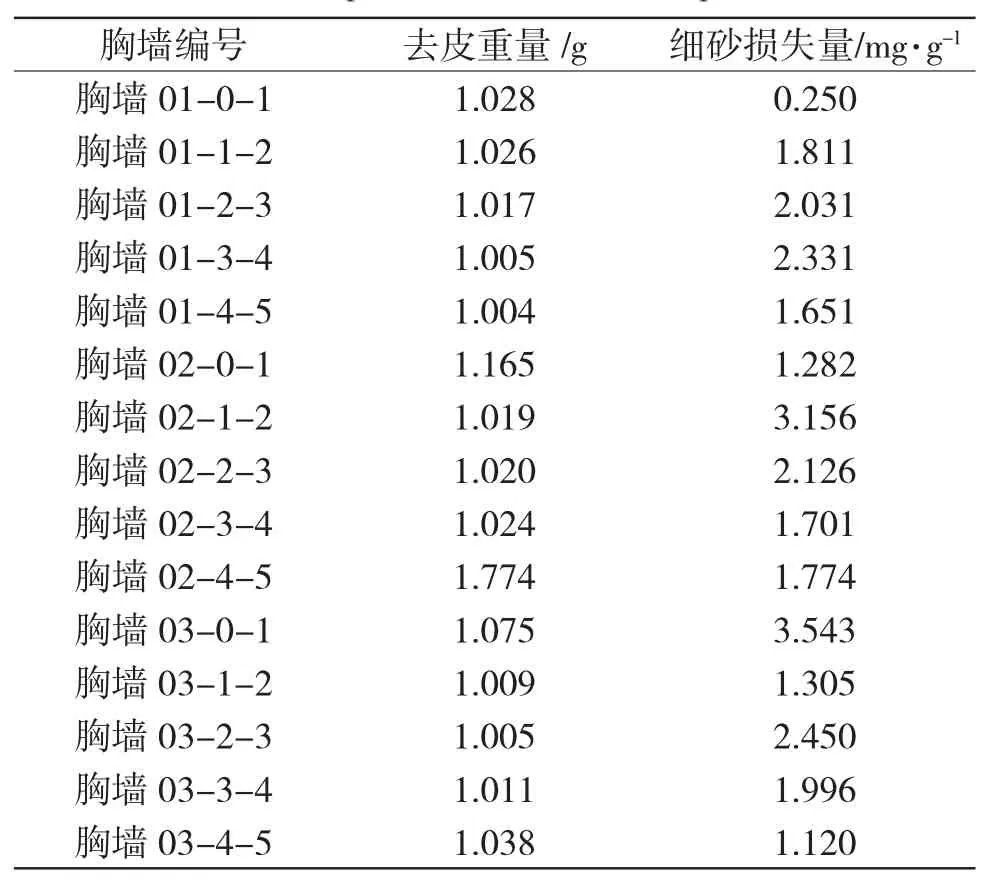
表1 准备的混凝土实验构件Tab.1 Prepared concrete test components

1.2 测定方法设计

1.2.1 混凝土Cl-扩散计算模型 由于Cl-在混凝土构件中以离子的形式扩散作用到混凝土中，因此，对于水灰比处于正常值的混凝土构件，将其中Cl-的扩散过程看作一个线性变化过程，见图1。

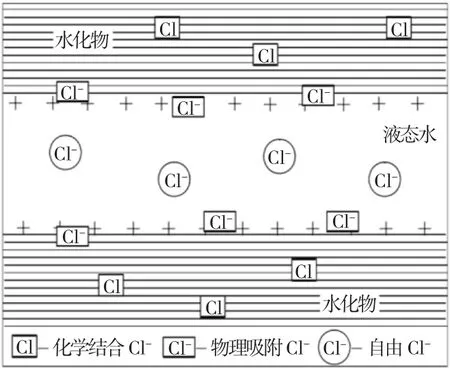
图1 混凝土中氯离子存在的状态Fig.1 Presence of chloride ions in concrete

由图1可见，Cl-存在状态，结合Fick第二定律可知，当Cl-进行一维扩散时存在以下关系：

式中J：扩散通量；D：扩展系数；C：Cl-浓度；t：扩散时间。使用扩展过程的质量守恒规律，得到混凝土构件中自由Cl-的二维控制方程，控制方程如下所示：

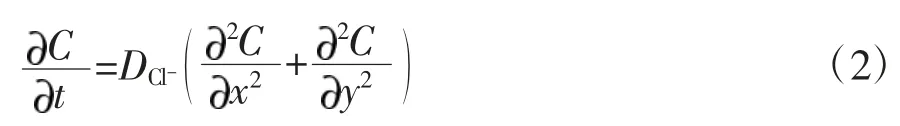
式中x：水平方向Cl-的扩散深度，y：竖直方向Cl-的扩散深度。基于均匀性假设，联立式（1）与式（2）可知总Cl-的浓度存在以下关系：

式中Cf：自由Cl-；Cb：结合Cl-的浓度，自用Cl-扩散系数为Df。

依照式（3）可得出混凝土Cl-的结合能力R，其计算方式如下：

利用式（4）来表征结合Cl-与自由Cl-之间的关系，可得到Cl-结合能力对扩散行为的影响变化曲线见图2。

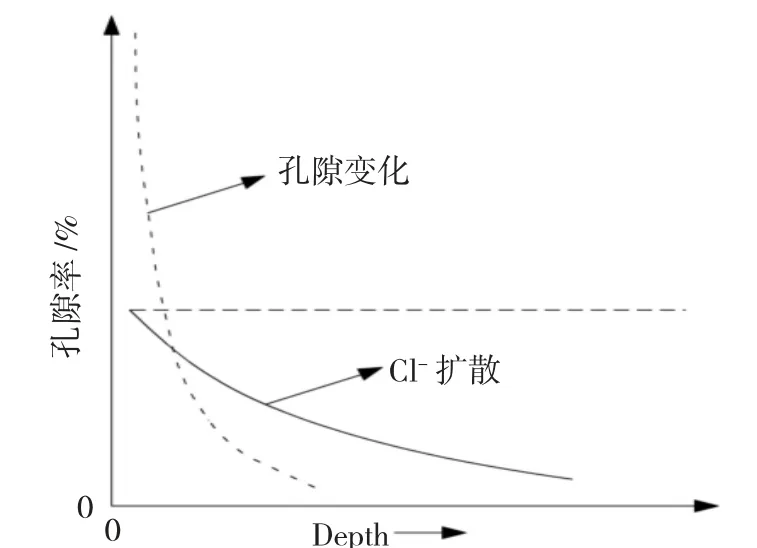
图2 Cl-结合能力变化对扩散行为的影响Fig.2 Influence of the change of chloride ion binding ability on diffusion behavior

由图2所示的变化关系，考虑Cl-的结合能力的变化，此时的表观Cl-扩散系数Da可定义为：

由式（5）可知，当混凝土中自由Cl-浓度按照第二扩展定律扩散时，此时的扩散系数转化为表观扩散系数[5,6]。当混凝土中的结合Cl-浓度为0，结合能力R为0时，表观扩散系数的数值与自由扩散系数相等，此时Cl-的扩散公式就可表示为:

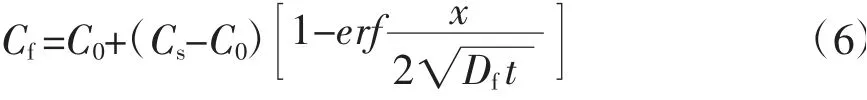
式中C0：混凝土内的初始Cl-浓度；Cf：扩散时间内游离状态的Cl-浓度；Cs：混凝土表面的Cl-浓度，erf表示误差函数，其函数关系服从：erfu=

由式（6）可知，在符合初始条件t=0，x＞0时，Cf=C0。此时混凝土Cl-浓度的游离状态的Cl-浓度和结合成分子的Cl-浓度成线性关系[7,8]。因此，将结合能力视为常数，结合初始条件对式（6）作变换处理，经计算可得到的Cl-扩散计算模型如下：

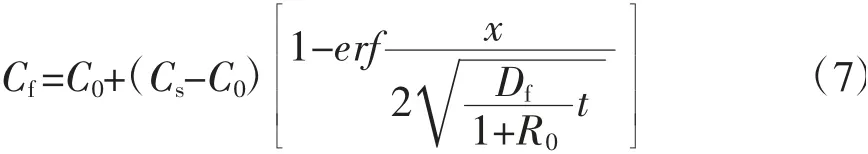
式中R0：Cl-结合能力常数。

综上计算得到混凝土中Cl-的扩散模型，利用此计算模型，分析Cl-浓度在混凝土中的分布边界元，完成对混凝土中Cl-含量的测定研究。

1.2.2 利用电位滴定法处理Cl-浓度分布边界元首先利用电位滴定法得到混凝土的电位滴定曲线的二次微分曲线，见图3。在此基础上，处理Cl-浓度分布边界元。

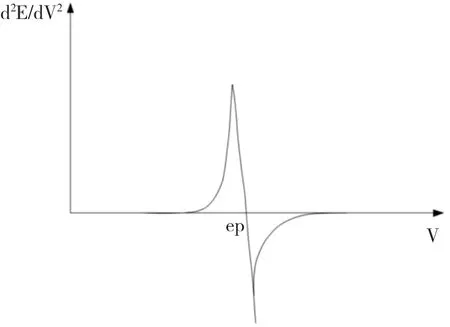
图3 电位滴定曲线的二次微分曲线Fig.3 Quadratic differential of the potentiometric titration curve

由图3所示的微分曲线，假定此时的混凝土呈现出均质各向同性，在此不考虑固化的Cl-，经实际计算可得到：

式（8）中存在：

由式（8）和式（9）可得边界条件为：

式中C：混凝土表面Cl-浓度；q：表明Cl-浓度梯度；Γ1Γ2：固化常量[9,10]。在此基础上，利用加权余量法处理式（9）和式（10）和得到边界奇异点积分方程如下：

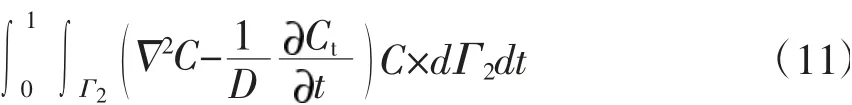
在处理上式得到的奇异点时，假设边界存在激励点和响应点，当两点重合时，边界奇异点积分方程可表示为：

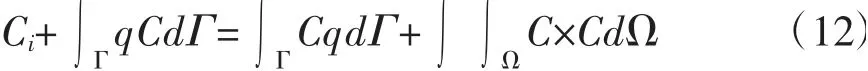
式中 Ω：激励点。此时采取一个微小半径圆弧绕过上点Ω，将源点包含在计算区域内[11]，将式（12）式改写为：

式中 ε：小半圆形成的边界；Γ-ε：原边界去除小半圆ε包含的原边界。计算微小半径圆弧上的Cl-浓度值，计算公式为：

式中 β：奇异点两侧做切线围成的角。

此时利用式（14）计算得到Cl-浓度分布边界元，使用这个边界元计算公式，计算可能解吸结合Cl-，保证混凝土中Cl-含量测定结果准确。

1.2.3 计算Cl-含量 在计算Cl-含量时，首先利用式（14），按照不同体积的混凝土，计算出混凝土中的砂浆孔隙率，计算结果见表2。

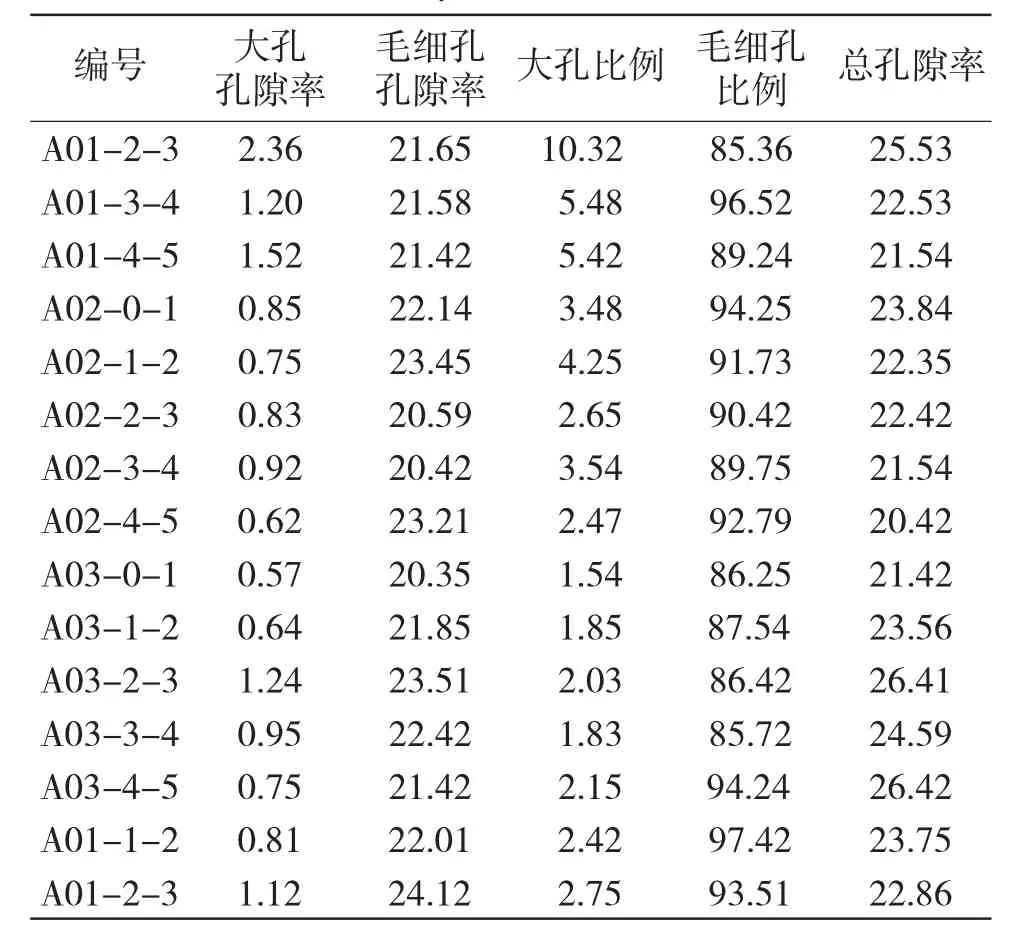
表2 混凝土砂浆孔隙率（%）Tab.2 Porosity of concrete mortar（%）

利用表2中的各项数据，将其整合为非线性相关分析回归方程，可得到下式：

式中a：大孔孔隙；b：毛细孔孔隙[12,13]。由此计算得到Cl-随着孔隙量的变化方程为：

式中W：孔隙量占比；C：混凝土质量；V：混凝土的体积；m：去孔隙混凝土质量。所以孔隙的可能解吸结合Cl-就可计算表示为：

式中a与b为常数。

由式（17）可知，固体细孔、裂隙和毛细管上的吸附层存在有限性，也就是Cb≠0，此时的吸附层数就变为单层，在吸附混凝土孔隙吸附Cl-时，混凝土固体表面就会存在氯离子吸附位，均匀分布在混凝土的表面[14,15]。

为了保证可能解吸结合Cl-含量测定结果准确，在确定Cl-的吸附参数时，在上式的基础上引入Temkin吸附，计算最终的可能解吸结合Cl-含量的公式为：

式中aT=0.1632，bT=0.8421，在扩散Cl-含量基础上，减去式（18）计算出的吸附部分的Cl-，即为最终测定得到的混凝土中Cl-含量。

2 Cl-测定

2.1 实验试剂

体积比为1∶1的HNO3与水混合液

0.02mol·L-1的Cl-标准溶液 称取0.6g NaCl固体，在105～110℃环境下烘制2h，然后置于烧杯中加水溶解，并转移到500mL容量瓶中加水稀释、摇匀。

0.02mol·L-1的AgNO3滴定液 称取2.0g Ag－NO3固体，置于烧杯中，加入适量水溶解后，转移到500mL容量瓶中加水稀释、摇匀，然后将其转入不透光容量瓶中，避光保存。

AgNO3标准滴定溶液的浓度计算过程如下：

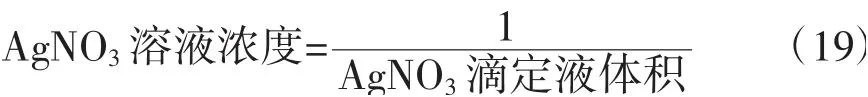
AgNO3滴定液对Cl-的滴定度计算过程如下：

95%乙醇溶液；蒸馏水。

2.2 仪器设备

天平（可精确至1×10-4g），烧杯，移液管，500mL容量瓶，梅特勒T50自动电位滴定仪，Cl-选择电极，双盐桥负荷电极。

2.3 实验过程

（1）称取混凝土样本2mg，加入1mL HNO3与水混合液，样本充分溶解后加如3mL乙醇溶液，用AgNO3标准液通过梅特勒T50自动电位滴定仪进行等当点滴定。

（2）称取混凝土样本5mg，加入3mL HNO3与水混合液，样本充分溶解后加如9mL乙醇溶液，用AgNO3标准液通过梅特勒T50自动电位滴定仪进行等当点滴定。

（3）称取混凝土样本10mg，加入5mL HNO3与水混合液，样本充分溶解后加如15mL乙醇溶液，用AgNO3标准液通过梅特勒T50自动电位滴定仪进行等当点滴定。

2.4 实验结果

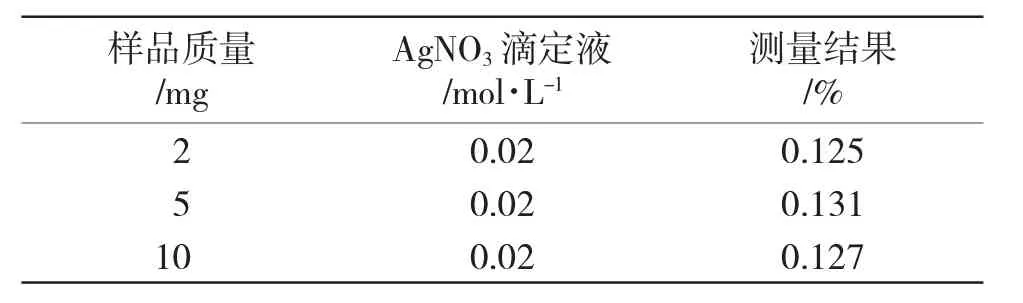
表3 实验数据汇总Tab.3 Experimental data summary

由表3可知，混凝土样品中，Cl-的含量占比随着样品质量的增加而有所变化，但这种变化量较小，说明实验所用混凝土样品中Cl-含量较为稳定。

3 方法有效性检验

为进一步测试基于电位滴定法的混凝土中Cl-含量测定方法的应用优势，设计如下实验加以检验。

使用实验准备的电位滴定仪测量实验准备各混凝件的Cl-含量，并将其作为标准值。然后分别使用文献[3]中的利用速测条法的Cl-含量测定方法、文献[4]的结合耦合多相传输的Cl-含量测定方法这两种传统Cl-含量测定方法与本研究所设计的基于电位滴定法的混凝土中Cl-含量测定方法进行实验，对比3种测定方法测量结果的准确性。基于上述实验准备，得到3种测定方法最终的实验结果，见图4。

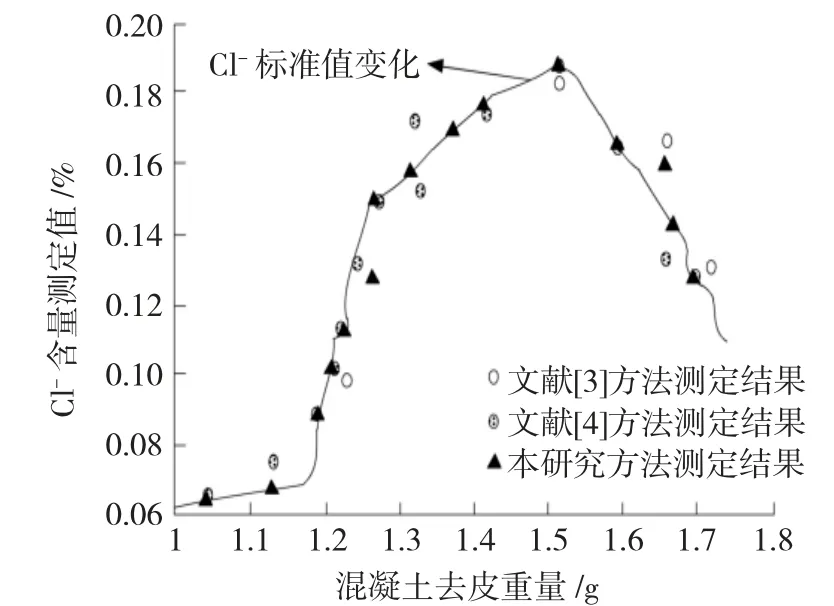
图4 3种测定方法测得到的Cl-含量结果Fig.4 Results of chlorine ion content measured by three methods

将梅特勒T50自动电位滴定仪测得的15个混凝土的重量和重量对应的Cl-浓度绘制为一条平滑的变化曲线，将一个混凝土的去皮质量作为横坐标，Cl-的浓度为纵坐标，将此作为一个Cl-数据点，共计15个数据点。定义偏离直线的数据点是存在误差的数据点，统计3种测定方法的偏离直线的数据点数量，偏离数量少的表示测定误差小。

由图4可知，文献[3]方法存在9个偏离数据点，文献[4]方法存在6个偏离数据点，而基于电位滴定法的混凝土中Cl-含量测定方法只存在2个偏离数据点，与两种传统测定方法相比，基于电位滴定法的混凝土中Cl-含量测定方法在实际测定时产生的误差最少，更适用于实际测定。

4 结语

混凝土中Cl-的含量是影响混凝土寿命的重要因素之一，对混凝土中Cl-的含量进行准确测定有利于优化混凝土的使用效果。传统的含量测定方法在实际计算时会出现大量偏离实际测量数值的数据点，针对这一不足，本研究构建混凝土扩散计算模型，分析Cl-分布边界元，计算Cl-可能解吸结合Cl-的含量，增加了测定方法在计算上的准确性。