外压与弯矩组合载荷作用下筛管压溃载荷计算

付光明, 彭玉丹, 孙宝江, 郭永宾,高永海, 蓝祖平, 金学义

(1.非常规油气开发教育部重点实验室(中国石油大学(华东)),山东青岛 266580; 2.中国石油大学(华东)石油工程学院,山东青岛 266580; 3.中海石油(中国)有限公司湛江分公司,广东湛江 524057; 4.海洋石油工程(青岛)有限公司,山东青岛 266520; 5.中海油田服务股份有限公司,河北三河 065201)

地层严重出砂会导致井筒砂堵、井壁坍塌,进而造成油气井产量下降,甚至停产等恶劣影响,是困扰疏松砂岩油气藏开发的主要因素之一[1-2]。目前,现场以筛管为主要工具的机械防砂方式为主[3-5];其中由完整套管打孔而成的基管是复合筛管的主要承载构件[6-7]。工程实际中,筛管在水平井及大位移井下入过程中会承受弯曲载荷和地层压力的联合作用[8-10];此外,在油气开采过程中,由于地层出砂严重或地层变形,筛管在巨大上覆岩层压力的作用下会发生弯曲变形[11-13]。当外界载荷超过筛管的极限承载能力时,会发生筛管压溃变形,严重威胁油气井的正常生产。目前,国内外学者对外压和弯曲组合载荷作用下完整管道的压溃强度[8-9][14-15]、纯弯矩作用下筛管的抗弯强度[16-18]和纯外压作用下筛管的压溃载荷[19-21]进行了大量研究,而关于外压与弯矩组合载荷作用下筛管压溃载荷计算的研究鲜有报道。因此开展针对组合载荷作用下筛管压溃载荷计算的研究具有重要意义。对此,笔者建立外压和弯曲组合载荷作用下平行布孔筛管强度有限元分析模型,分析筛管弯曲强度的变化,研究弯曲载荷加载方向和椭圆度等对筛管压溃载荷的影响,讨论外压和弯曲载荷联合作用下,不同布孔参数筛管的压溃载荷变化,基于以上数值计算结果,建立外压和弯曲组合载荷下筛管压溃载荷计算公式。

1 有限元模型建立

1.1 模型假设

根据平行布孔筛管结构及其载荷边界条件的对称关系,建立二分之一对称模型,如图1所示,选取二十节点六面体二次减缩积分单元(C3D20R);该单元在较大弯曲变形条件下不容易发生剪切自锁现象,适合求解筛管变形较大和存在应力集中的情况[22]。该模型在发生严重扭曲下,仍具备较高的分析精度。选取筛管的轴向长度为10D,其中D为筛管的名义直径。为减小孔眼处应力集中和严重的扭曲变形对模型求解精度的影响,对孔眼局部区域网格加密处理。通过对网格数的敏感性分析,确定可以保证模型的计算精度的最低网格数。假定筛管的初始椭圆度分布[23]满足:

(1)

其中

式中,ω0为极坐标系下径向位移,mm;Δ0为筛管初始椭圆度;x为轴向坐标;β为初始椭圆度沿x方向延伸的相关系数;D为筛管名义直径,mm;Dmax和Dmin分别为筛管最大直径和最小直径,mm;θ为极坐标下的角度,rad。

1.2 载荷及边界条件

图1 筛管模型及有限元模型边界条件Fig.1 Finite element model and boundary conditions

考虑筛管模型几何和载荷条件的对称性,假定边界条件如图1所示。其中对称平面1处施加关于yoz平面的平面对称约束条件;平面2处施加x、y和z方向固支约束;平面3上施加限制x和y方向的平动位移,即U1=U2=0,其中U1为x方向的位移,U2为y方向的位移。在筛管端部(平面3)中心点处设立参考点,并定义该参考点与筛管端部的耦合条件[14-15]。在筛管的外表面,施加垂直于筛管表面的均布压力,在参考点上施加转角或弯矩载荷,加载路径为先施加弯矩后再施加外压,直至筛管发生压溃变形,并通过Risk分析方法确定筛管的临界压溃载荷。

2 参数化分析

2.1 筛管几何和材料参数

选取实际工程中常用的筛管尺寸和结构参数,如表1所示。筛管材料为N80钢,弹性模量为203 GPa,泊松比为0.3,屈服强度为464 MPa,假定材料为各向同性强化,真实应力-应变的关系曲线如图2所示。

表1 筛管的几何结构参数Table 1 Geometric parameters of sand control screen

图2 筛管材料的应力-应变曲线Fig.2 Stress-strain curve of sand control screen material

2.2 筛管弯曲过程中弯矩-转角的关系

纯弯作用下,筛管的弯矩随转角变化如图3所示。随转角的增大,筛管的弯矩变化可分为3个阶段:第1阶段,随着转角的增加,筛管弯矩呈线性上升;第2阶段,随着转角继续增大,弯矩增大的速度逐渐减慢,直至转角增大到临界转角θcr,弯矩到达临界弯矩Mcr,筛管孔眼在弯矩作用下首先发生塑性变形,如图4所示;第3阶段,在弯矩到达临界值后,随着转角继续增大,孔眼周围的塑形变形加剧,筛管抗弯能力急剧下降(图3)。在筛管孔眼未发生塑变形之前,不同径厚比筛管的弯矩-转角曲线,如图5所示。由图5可知,在筛管外径相同条件下,不同径厚比筛管,弯矩随转角的变化规律类似:弯矩随着转角增大而增大;但在相同转角下,筛管的径厚比越大,对应的弯矩值越小,筛管的抗弯能力越弱。

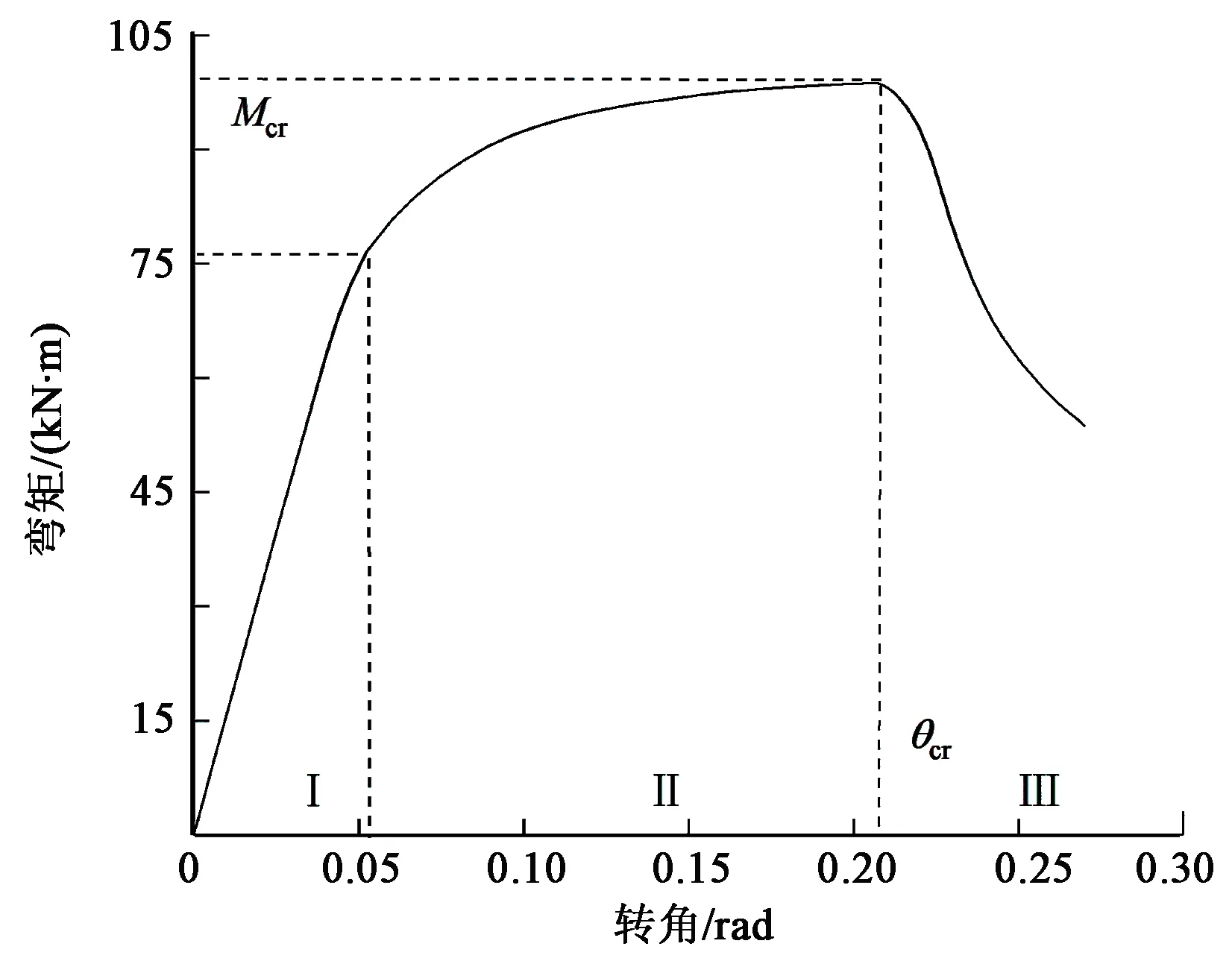
图3 弯曲条件下筛管的弯矩-转角关系Fig.3 Moment-rotation angle curve of screen under bending

图4 纯弯作用下筛管孔眼处变形情况Fig.4 Plastic deformation around holes of screen pipe under pure bending

图5 纯弯作用下不同径厚比筛管的弯矩-转角关系Fig.5 Moment-rotation angle curve with different D/t under pure bending

2.3 转角加载方向和椭圆度对筛管压溃载荷的影响

2.3.1 转角沿椭圆短轴加载时椭圆度对筛管压溃载荷的影响

取孔径为12.7 mm,轴向孔为17,周向孔为12,径厚比为21的筛管,在参考点上施加沿筛管椭圆截面短轴方向转角,如图6所示。计算不同椭圆度下转角沿椭圆短轴加载时筛管压溃载荷变化。转角沿短轴加载时,筛管的压溃变形沿着椭圆的短轴发生。不同椭圆度和转角下筛管压溃载荷变化如图7所示。随着转角的增大,筛管压溃载荷逐渐减小,且筛管压溃载荷的下降速度逐渐减缓,原因在于转角增大的后期,弯矩增大速度逐渐减小。相同条件下,与转角为零时的筛管压溃载荷相比,筛管压溃载荷和压溃载荷降低程度随椭圆度的增大而减小。

图6 沿椭圆短轴加载转角载荷时筛管的压溃变形Fig.6 Collapsed deformation of sand control screen when loading direction along minor axis

图7 不同椭圆度和转角条件下筛管压溃载荷变化Fig.7 Collapse pressure of screen pipe under different ovality and rotation angle

2.3.2 转角沿椭圆长轴加载时椭圆度对筛管压溃载荷的影响

转角沿椭圆长轴加载时筛管压溃载荷变化如图8所示。由图8(a)可以看出,不同椭圆度下,筛管压溃载荷随转角增大的变化情况大致可分为3个阶段:第1阶段,在转角增大的初期,筛管压溃载荷逐渐减小;第2阶段,随着转角继续增大,筛管压溃载荷开始逐渐增加,并达到峰值;第3阶段,筛管压溃载荷到达峰值后,随着转角继续增大,筛管压溃载荷开始减小。椭圆度越大,筛管压溃载荷的峰值越小,峰值对应的转角越大。

图8 外压与弯矩组合载荷作用下转角沿椭圆长轴加载时筛管的压溃变形Fig.8 Collapsed deformation when rotation angle loaded along major axis under combined bending and external pressure loads

产生上述现象的原因在于转角沿椭圆长轴加载时对筛管的椭圆度有一定的校正作用:在转角较小时,这种校正作用不明显,筛管压溃载荷随着转角的增大而较小;在转角增大到一定程度后,筛管整体的椭圆度逐渐减小,筛管的压溃载荷逐渐增大,筛管的压溃载荷随着转角的增大而增大,且筛管的压溃变形形态可能会发生变化;随着转角继续增大,弯曲对椭圆度的校正作用将达到最大,此时筛管的压溃载荷达到峰值,之后随着转角的增大,筛管压溃载荷逐渐降低。由图8(a)可知,筛管的压溃载荷的峰值小于筛管不发生弯曲时的压溃载荷,表明弯曲对筛管的椭圆度的校正作用有限。

椭圆度为0.15%与椭圆度为0.25%、0.35%、0.5%压溃载荷变化曲线不同的原因在于弯曲作用对筛管椭圆度的校正作用,使筛管的压溃变形形态发生了改变。通过输出筛管压溃变形的云图可知:对于椭圆度为0.15%的筛管,转角小于0.1时,筛管的压溃变形是沿椭圆的短轴发生,如图8(b)所示;转角增加到0.1后,弯曲对椭圆度产生了较大影响,筛管的压溃变形从沿短轴方向发生转变为沿椭圆度的长轴发生,如图8(c)所示;随着转角继续增大,筛管的压溃变形一直沿长轴发生。对于椭圆度为0.25%的筛管,转角小于0.18时,筛管的压溃变形沿椭圆短轴发生,转角增加到0.18时,筛管的压溃变形从沿短轴方向发生转变为沿椭圆度的长轴发生,随着转角继续增大,筛管孔眼周围发生塑性变形,对筛管椭圆度产生了一定影响,筛管的压溃变形从沿长轴方向发生转变为沿椭圆度的短轴发生;对于椭圆度为0.35%和0.5%的筛管,由于椭圆度较大,弯曲对椭圆度的校正作用有限,转角增大到筛管孔眼发生塑性变形后,筛管的压溃变形一直沿着短轴发生。

通过对比转角沿椭圆短轴和长轴加载的过程中筛管的压溃载荷可知,相同条件下,弯矩沿椭圆长轴加载的筛管压溃载荷要普遍大于弯矩沿短轴加载的情况;与转角沿椭圆短轴加载的筛管压溃载荷相比,椭圆度为0.5%时,沿长轴加载时筛管压溃载荷的最大增幅度为19.5%;椭圆度为0.35%,最大增幅度为21.0%;椭圆度为0.25%,最大增大幅度为21.7%;椭圆度为0.15%,最大增大幅度为18.2%。

2.4 弯矩载荷对筛管压溃载荷的影响

取孔径为12.7 mm、轴向孔为17、径向孔为12筛管,转角沿椭圆度的短轴加载时,计算在极限转角范围内不同径厚比筛管的压溃载荷变化,如图9所示。

图9 均布外压和弯矩组合载荷作用下 不同转角、径厚比筛管压溃载荷Fig.9 Collapse pressure of sand control screen under different D/t and rotation angle in combined load conditions

由图9可知,随着转角(弯矩载荷)的增大,筛管压溃载荷逐渐降低,筛管压溃载荷的降低速度逐渐减小,压溃载荷曲线趋于平缓,原因在于转角增大到一定程度后,筛管弯矩增大幅度很小;相同条件下,径厚比越大,筛管压溃载荷越小,对于不同径厚比的筛管,筛管的压溃载荷降低程度不同:转角的比例系数由0增大到0.9时,筛管径厚比为16时,筛管压溃载荷降低14%;筛管径厚比为21时,筛管压溃载荷降低23%;筛管径厚比为26时,筛管压溃载荷降低26%;径厚比越大,筛管压溃载荷下降程度越大,筛管弯曲对筛管压溃载荷的影响越明显。

2.5 布孔参数对筛管压溃载荷的影响

2.5.1 孔径、周向孔数

选取轴向孔数为17的筛管,在筛管端部施加20 kN·m的弯矩,弯矩的方向沿椭圆的短轴加载,分析不同孔径和周向孔数等参数下筛管的压溃载荷变化,如图10所示。在孔径相同的条件下,筛管压溃强度随着周向孔数的增加而降低。在周向孔数相同的条件下,随孔径增加,压溃载荷下降较为明显。当孔径为6.35 mm时,周向孔数为8的筛管压溃载荷降幅最小,约为5.5%;周向孔数为16的筛管压溃载荷降幅最大,约为8.0%。通过计算可知,在均布外压和弯矩组合载荷作用下,相比于周向孔数,孔径对筛管压溃载荷的影响较为明显。

图10 不同孔径、周向孔数情况下筛管的压溃载荷Fig.10 Collapse strength of sand control screen under different hole diameters and circumferential holes

2.5.2 孔径、轴向孔数

选取周向孔数为12,在筛管端部施加20 kN·m的弯矩,弯矩的方向沿椭圆的短轴加载,分析不同孔径和轴向孔数下筛管的压溃载荷,如图11所示。从图11可知,在同一孔径条件下,随轴向孔数增加,筛管压溃载荷逐渐降低。轴向孔数一定的条件下,随着孔径的增加,筛管压溃载荷下降明显。计算结果表明,孔径对筛管压溃载荷的影响较大。

图11 不同孔径、轴向孔数下筛管的压溃载荷Fig.11 Collapse strength of sand control screen under different hole diameters and axial hole number

3 筛管压溃载荷计算公式

为了简化筛管压溃载荷计算,方便现场工程的实际需求,建立外压和弯矩组合载荷条件下,弯矩沿椭圆短轴加载时筛管压溃载荷的计算公式。假设弯曲条件下筛管的压溃载荷与布孔参数、筛管弯矩和布孔前的压溃载荷和弯矩有关,满足:

(2)

其中

C=πD/N.

式中,G为筛管的压溃载荷系数;Pb为弯曲条件下筛管压溃载荷,MPa;P0为对应布孔前套管的压溃载荷,MPa;f为引入的函数;d为孔径,mm;L为轴向孔间距,mm;C为周向孔间距,mm;N为周向孔数;M0为布孔前套管的极限弯矩,N·m;M为作用在筛管上的弯矩,N·m;Mcr为纯弯矩作用下筛管的极限弯矩载荷,M≤Mcr≤M0。

引入无量纲参数d/C、d/L、M/M0, 式(2)表示为

(3)

假定式(3)可表示为

(4)

其中F、F1、F2为待确定的函数关系。假定该函数可展开为幂级数形式[24-25],

(5)

式中,Am和Bn为展开式系数;m和n为展开式的阶次;α1、α2和β1为展开式各项阶次。

考虑筛管的压溃载荷小于布孔前套管的压溃载荷,即:Pb/P0≤1,当m=n=0时,可得A0B0=1;n=0表示纯外压条件,式(5)参数A0=1,故可求得B0=1。若忽略式(5)中高阶小量,可近似表示为

(6)

分析了135组不同径厚比、孔径和孔间距等筛管在均布外压和弯矩组合载荷作用下的压溃载荷有限元数值计算结果,得到筛管压溃载荷系数与孔径、周向孔间距、轴向孔间距和弯矩的关系,如图12所示。通过参数化分析,拟合得到压溃载荷系数与布孔参数以及弯矩载荷的关系为

(7)

式(7)为筛管压溃载荷系数与孔径、孔间距以及弯矩载荷之间的关系,其中完整管道压溃载荷P0和极限弯矩载荷M0可以通过DNV、API等规范公式和数值模拟求解。当M=0时,式(7)可简化为均布外压作用下筛管压溃载荷计算公式。

由于缺乏组合载荷作用下筛管的压溃试验研究的文献资料,本文中选取纯外压作用和弯矩载荷分别为筛管的极限弯矩载荷的10%、30%和50%时的有限元结果来验证建立公式的准确性。选取筛管的基本参数[21]如表2所示。

纯外压作用(M=0)以及外压和弯矩组合载荷作用下筛管的压溃载荷计算结果如表3所示。其中Pb-Ana和Pb-FEM分别表示由式(7)和数值模型求得的筛管压溃载荷;采用DNV规范[26]计算式(7)参数P0,表3中M0-Ana由文献[27]中公式计算。在纯外压作用下,建立的经验公式计算结果与试验结果[21]的平均误差为8.9%,最大误差为-14.65%。随着弯矩载荷的增加,筛管的压溃载荷逐渐降低,且建立的公式计算结果能较好地反映有限元结果。

将外压和弯矩组合载荷作用下筛管压溃载荷的经验公式计算结果和有限元计算结果进行比较,结果如图13所示。两者的整体误差小于10%,平均误差为2.7%。表明建立的经验计算公式可较为准确地计算外压和组合载荷作用下筛管的压溃载荷。

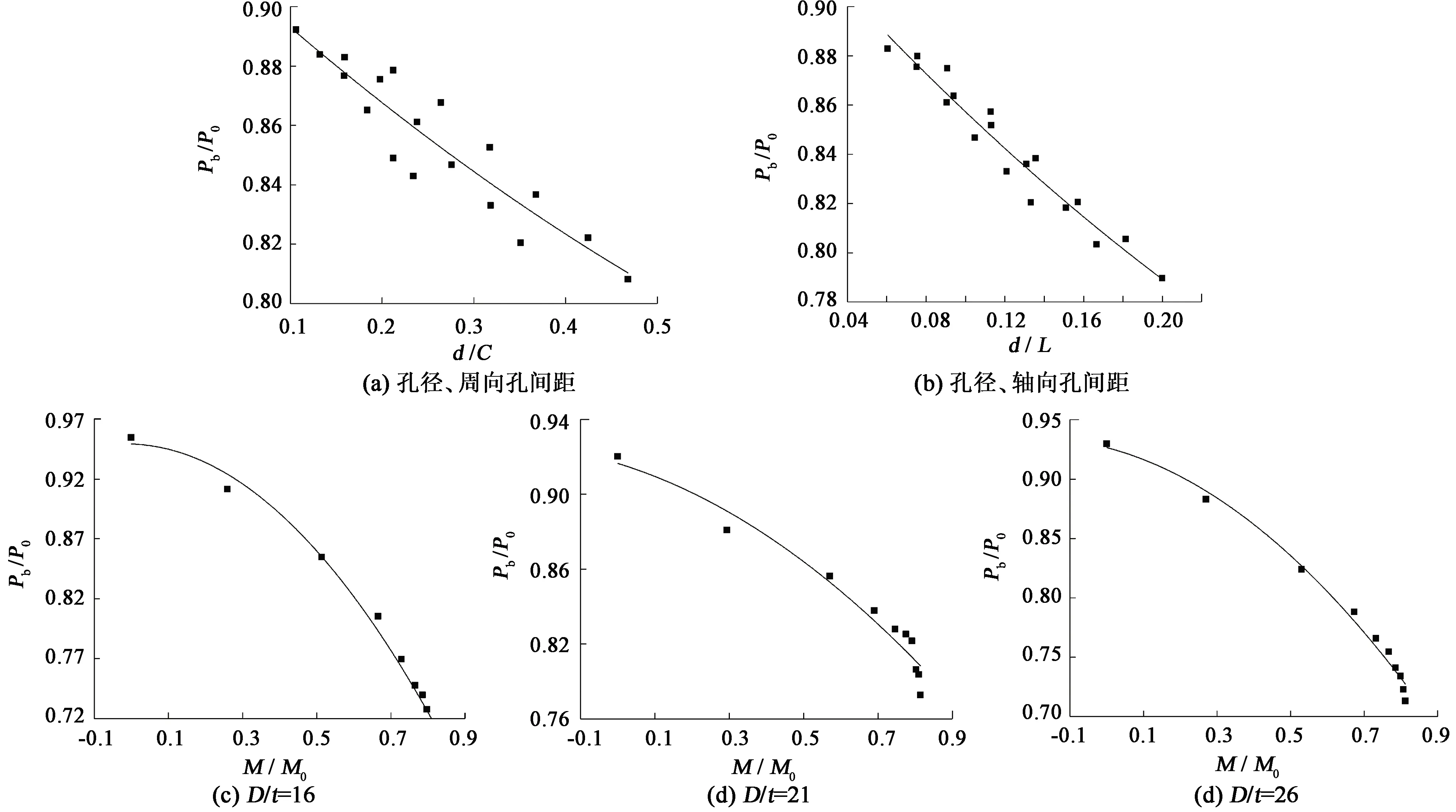
图12 筛管压溃载荷系数与孔径、周向孔间距、轴向孔间距和弯矩的关系Fig.12 Collapse pressure factor varying with different hole diameters, axial hole spacing, circumferential hole spacing and bending moment

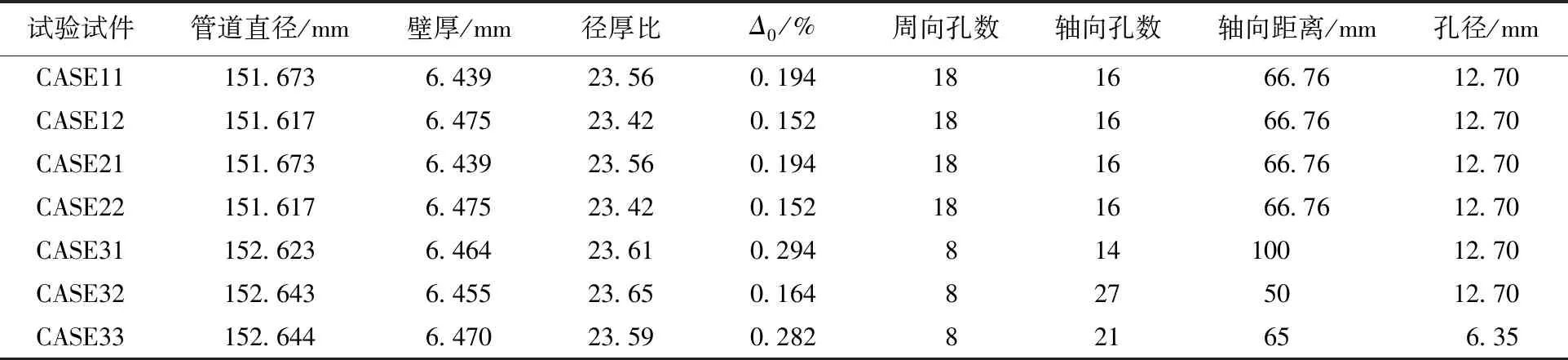
表2 试验筛管几何参数

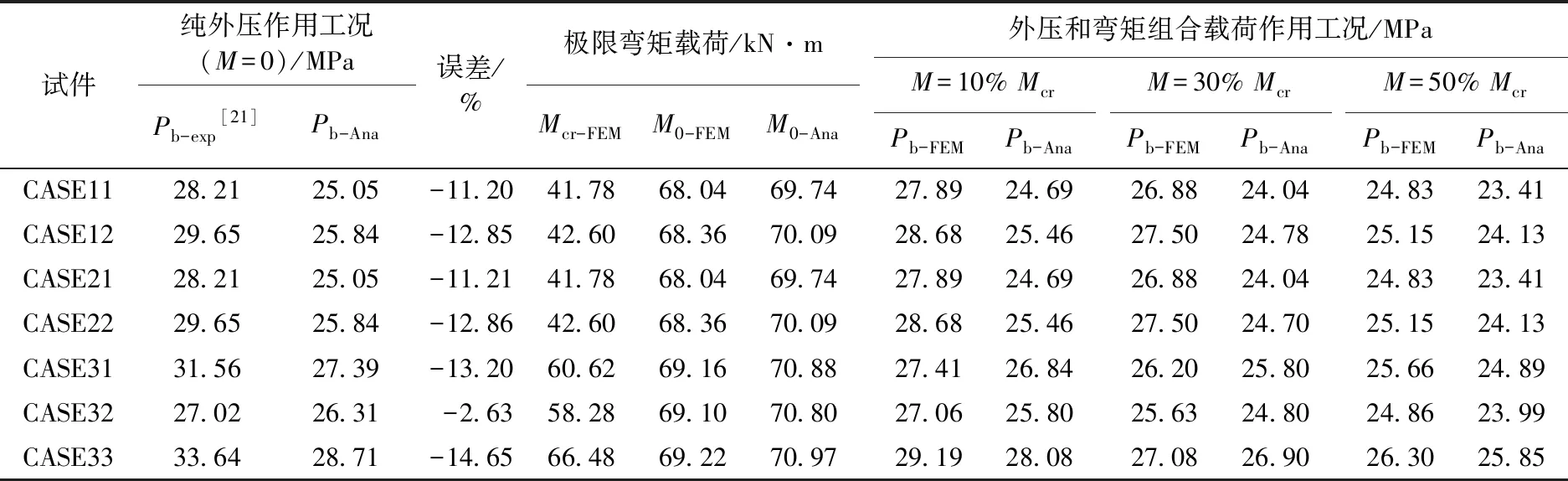
表3 外压与弯矩组合载荷作用下筛管压溃载荷与试验结果[21]和有限元结果对比Table 3 Collapse strength comparison between experimental test[21], numerical results and results calculated by empirical equation under combined external pressure and moment condition

图13 有限元数据和拟合公式计算数据对比Fig.13 Comparisons between numerical and analytical results

4 结 论

(1)建立的弯曲和外压组合载荷下筛管压溃载荷简化公式计算结果与有限元结果的平均误差小于2.7%。

(2)沿椭圆的长轴加载弯矩时筛管的压溃载荷会存在峰值,在相同条件下,弯矩沿椭圆长轴加载的筛管压溃载荷普遍大于弯矩沿短轴加载情况。

(3)弯矩载荷对筛管的压溃载荷影响明显,随着弯矩载荷的增加,压溃载荷逐渐降低。