弯曲载荷下不同布孔形式筛管极限弯矩分析*

郭凯毅 付光明 彭玉丹 李明亮 朱秉剑 庹宇航

(1.中国石油大学(华东)新能源学院 2.中国石油大学(华东)石油工程学院 3.大港油田石油工程研究院 4.中石油新疆油田分公司陆梁油田作业区 5.中国石油天然气管道工程有限公司)

0 引 言

我国疏松砂岩油气资源丰富且分布广泛。然而，地层出砂经常出现在疏松砂岩油气藏的开发过程中且已经成为困扰疏松砂岩油气田高效开发的难题之一[1-2]。为防止大量的地层砂进入井筒，需要采取合理的防砂措施。其中，机械防砂完井是油田现场重要的防砂方式之一[3-4]。而筛管是机械防砂完井的主要工具，在防砂过程中起着至关重要的作用[5-6]。现场常用绕丝筛管和复合筛管等精密筛管，其主要的承载部件为打孔基管。

油气田现场为上产增效，常采用超短半径水平井和大位移井对油气藏进行开采。在水平井和大位移井防砂完井过程中，筛管下入通过弯曲井段时，由于井眼的弯曲角度大，会承受巨大的弯曲载荷[7-8]。由于孔眼的存在会严重降低筛管的承弯能力，筛管在通过弯曲井段时容易发生屈曲变形和孔眼位置的塑性断裂，从而导致筛管防砂失效，进而严重影响油气井的产能。因此，研究弯曲载荷下筛管的极限承载能力具有重要意义。

目前，关于筛管强度的研究集中于外压载荷下筛管强度分析，而关于筛管弯曲强度的研究较少且没有针对不同布孔形式的筛管进行系统的研究，给现场弯曲载荷作用下筛管强度评价和布孔参数选择带来了一定困扰。孙宝江等[9-10]建立了外压作用下和外压与弯矩联合载荷作用下筛管抗挤强度的经验公式；彭玉丹等[11-12]分析了外压作用下不同布孔形式筛管抗挤强度变化规律，并提出了相应的计算公式和布孔参数优化方法；黄中伟等[13]和张恒等[14]基于试验和有限元方法分析了弯曲载荷作用下不同类型割缝筛管的极限弯曲强度；李喆等[15]利用ANSYS软件分析了复合筛管在经过不同曲率的水平井弯曲段时筛管外护套和基管的应力变化规律；贾宗文等[16]和曹银萍等[17]基于试验和理论方法分析了套管在弯曲井段的抗挤压强度。

本文基于弹塑性理论，利用ABAQUS有限元软件建立了弯曲载荷作用下平行、交错和螺旋布孔形式筛管的有限元模型，系统分析了弯曲载荷作用下不同布孔形式和布孔参数对筛管极限弯矩的影响规律。所得结果可为筛管布孔形式的选择及参数优化提供重要参考。

1 有限元模型建立及模拟结果分析

1.1 筛管布孔形式

筛管的主要布孔形式为螺旋布孔、交错布孔和平行布孔[11]，如图1所示。由于平行布孔和交错布孔具有对称性，取平行布孔和交错布孔的模型以简化计算，如图2a和图2b所示；由于螺旋布孔筛管不具有对称性，采用如图2c所示的全尺寸模型。采用C3D8R单元对筛管有限元模型进行网格划分，其优点在于筛管发生严重弯曲变形时单元不易发生剪切自锁，并且具有很好的位移和应力求解精度[18-20]。筛管的长度取值大于筛管外径的8倍。此外，假设筛管不存在椭圆度和偏心等缺陷。

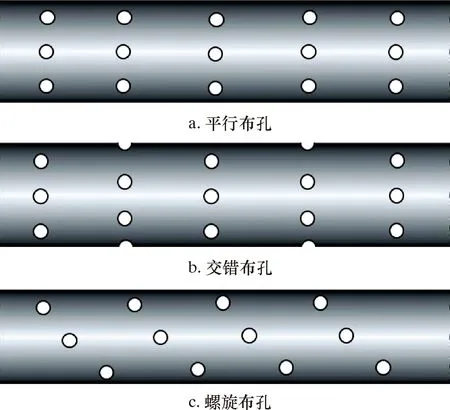
图1 筛管的3种布孔形式Fig.1 Three hole patterns for screen pipe

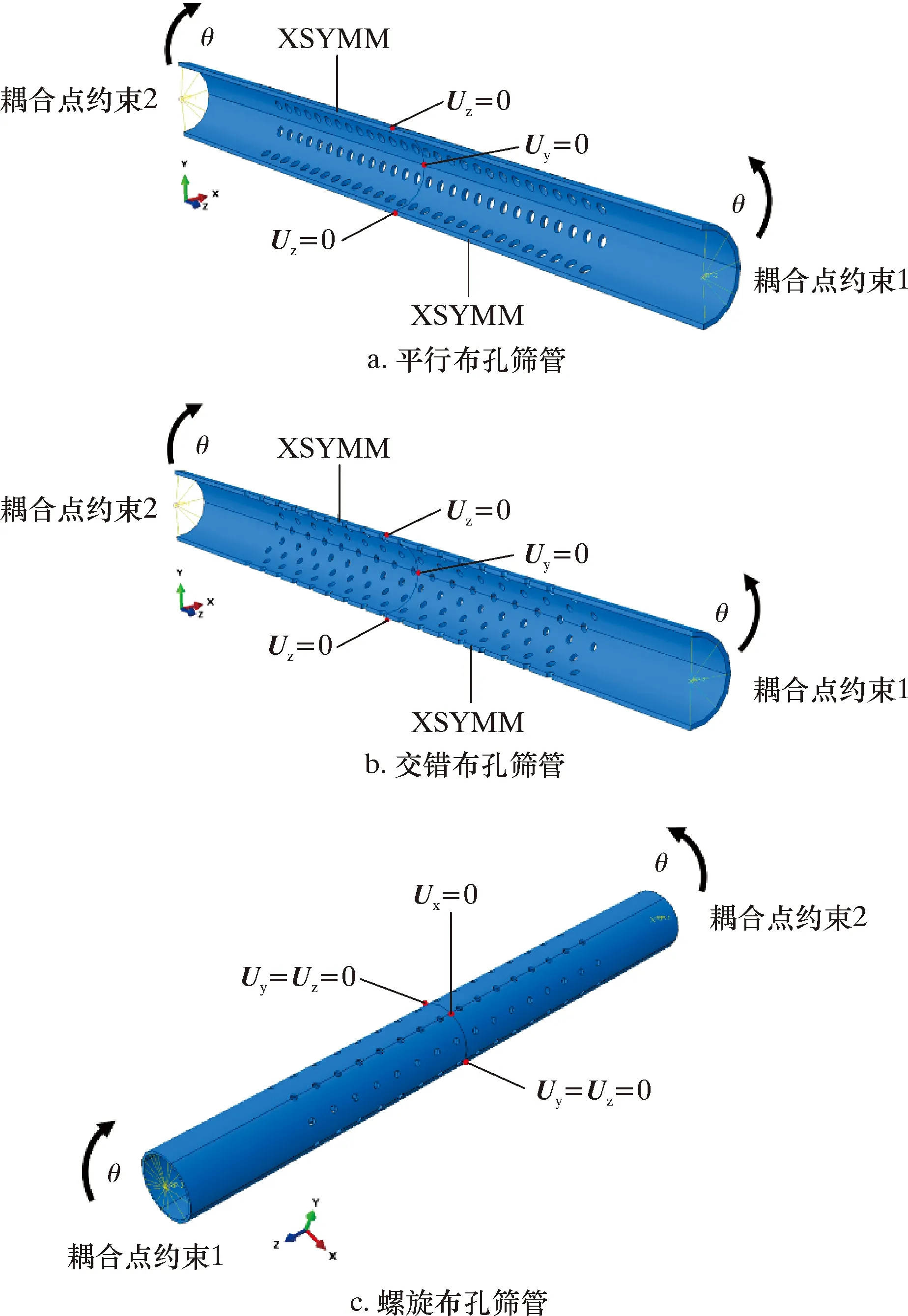
图2 3种布孔形式筛管的有限元模型及边界条件Fig.2 Finite element models and boundary conditions of three hole patterns for screen pipe

1.2 载荷及边界条件

为施加弯曲载荷，在筛管的两端创建耦合点与筛管的2个端面耦合。通过在筛管两端的耦合点施加转角使筛管发生弯曲变形[21]，如图2所示。由于平行布孔和交错布孔筛管都具有对称性，在对称平面施加对称约束，同时在筛管中间截面上的相关节点施加关于Z和Y方向的位移约束(Uz=Uy=0)以克服加载过程中的刚体位移。螺旋布孔的边界条件如图2c所示，在两端的耦合点上施加转角，在筛管中间截面上相关节点施加关于X(Ux=0)、Z和Y(Uz=Uy=0)方向的位移约束以克服加载过程中的刚体位移。

1.3 筛管材料参数

筛管材料的屈服强度为463.64 MPa，弹性模量为203 GPa，泊松比为0.3，材料的性能取为各向同性。

1.4 数值模拟结果分析

通过输出筛管转角-弯矩曲线确定筛管的极限弯矩。由于3种布孔形式筛管的转角-弯矩曲线相似，为此取交错布孔筛管的转角-弯矩曲线进行分析，如图3所示，其他布孔形式的在此不再赘述。由图3可知，随着转角的增大，筛管的弯矩变化可以分为4个阶段，具体如下：第1阶段，随着转角的增大，筛管弯矩呈直线急剧增加，此时筛管的应力和弯曲变形较小，如①所示；第2阶段，随转角继续增大，筛管的弯矩逐渐增大而增加速度逐渐减小，筛管的应力和弯曲变形逐渐增加，如②所示；当筛管的转角增大到极限转角θcr，筛管的弯矩达到极限弯矩Mcr，此时筛管整体的应力达到最大值，如③所示；第3阶段，当转角大于θcr，随转角继续增大，筛管的极限弯矩以较小的速度逐渐降低，筛管的弯曲变形继续增大而应力变化较小，筛管发生塑性变形，如④所示；第4阶段，随转角继续增大，筛管的极限弯矩急剧减小而筛管的弯曲变形急剧增大，此时筛管中部发生屈曲变形，筛管整体的应力逐渐减小，如⑤所示。

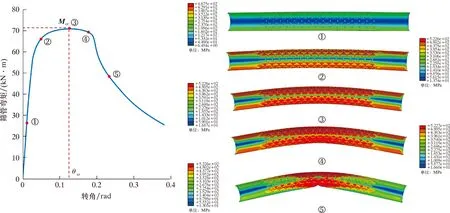
图3 筛管转角-弯矩曲线及数值模拟结果Fig.3 Corner-bending moment curve and numerical simulation results of screen pipe

2 参数优化分析

取工程中常用的筛管参数，如表1所示，建立3种布孔形式下筛管的有限元模型，分析布孔形式及布孔参数对筛管极限弯矩的影响规律。

表1 筛管几何参数Table 1 Geometric parameters of screen pipe

2.1 径厚比和孔密对筛管极限弯矩的影响

孔径取9.5 mm，建立3种布孔形式下筛管的有限元模型，分析孔密和径厚比(D/t)对筛管极限弯矩的影响规律，结果如图4所示。由图4可知，相同布孔形式下，筛管的极限弯矩随着孔密的增大而减小。对于不同布孔形式的筛管，不同孔密区间内筛管极限弯矩变化规律不同，大致可以分为4个区域(Q1、Q2、Q3、Q4)，如图4所示。在Q1区域，随孔密增大，3种布孔形式筛管的极限弯矩和极限弯矩降低速度相差较小。在Q2区域，随孔密增大，交错布孔筛管极限弯矩降低速度小于其他2种布孔方式，而平行布孔筛管的极限弯矩降低速度小于螺旋布孔；此范围内，交错布孔筛管的极限弯矩大于其他2种布孔形式，同时，平行布孔筛管的极限弯矩大于螺旋布孔筛管的极限弯矩。在Q3区域，随孔密的增大，交错布孔筛管极限弯矩降低速度增大并逐渐大于其他2种布孔方式，而螺旋布孔筛管的极限弯矩降低速度要小于平行布孔筛管；在此区域，交错布孔筛管的极限弯矩仍大于其他2种布孔形式，而平行布孔筛管的极限弯矩小于螺旋布孔筛管的极限弯矩。在Q4区域，交错布孔筛管极限弯矩降低速度最大，而螺旋布孔筛管的极限弯矩降低速度要小于平行布孔筛管；在此区域内，螺旋布孔筛管的极限弯矩最大，交错布孔筛管的极限弯矩最小。对于不同径厚比的筛管，其他条件相同的条件下，D/t=19.35的筛管极限弯矩最大，D/t=23.64的筛管次之，D/t=16.89的筛管极限弯矩最小。由于这3种径厚比筛管的外径不一致，由完整管道的极限弯矩计算模型可知[18]，筛管的极限弯矩同时与管径D和壁厚t相关，而D对筛管的极限弯矩的影响显著。

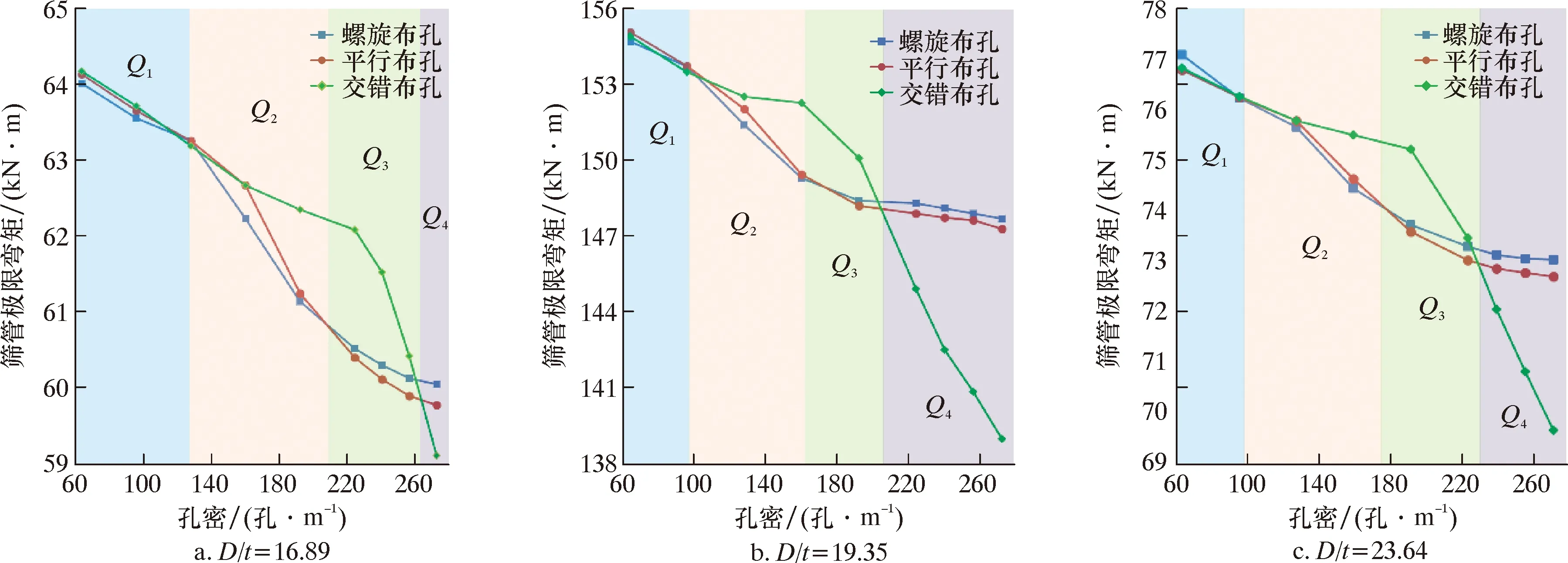
图4 孔密和径厚比对筛管极限弯矩的影响Fig.4 Effect of hole density and radius-thickness ratio on ultimate bending moment of screen pipe

以D/t=19.35为例，计算结果表明：当孔密小于96孔/m时，3种布孔形式筛管的极限弯矩相差较小；当孔密介于96～204孔/m时，交错布孔形式筛管极限弯矩最大，在此孔密区间筛管推荐采用交错布孔形式；当孔密大于204孔/m时，螺旋布孔筛管极限弯矩最大，在此孔密区间筛管推荐采用螺旋布孔形式。

2.2 径厚比和孔径对筛管极限弯矩的影响

孔密取128孔/m，建立3种布孔形式下径厚比和孔径下筛管的有限元模型，分析不同径厚比和孔径对筛管极限弯矩的影响规律，结果如图5所示。由图5可知，相同布孔形式下，筛管的极限弯矩随孔径的增大而减小。随孔径的增大，筛管的极限弯矩近似呈直线下降。不同径厚比下，筛管的布孔形式对筛管的极限弯矩影响程度不同：当D/t=16.89，在其他参数相同条件下，不同布孔形式筛管极限弯矩相近似相等；当D/t=19.35，其他参数相同条件下，交错布孔筛管的极限弯矩大于其他2种布孔形式，螺旋布孔筛管的极限弯矩最小；当D/t=23.64，在孔径小于9.5 mm时，3种布孔形式的筛管极限弯矩近似相等，随孔径增大，交错布孔筛管的极限弯矩大于其他2种布孔形式，而螺旋布孔筛管的极限弯矩最小。对于不同径厚比的筛管，其他条件相同的条件下，D/t=19.35的筛管极限弯矩最大，D/t=23.64的筛管次之，D/t=16.89的筛管极限弯矩最小，原因与上节类似，在此不再赘述。

图5 孔径和径厚比对筛管极限弯矩的影响Fig.5 Effect of hole size and radius-thickness ratio on ultimate bending moment of screen pipe

以D/t=19.35为例，计算结果表明：随孔径的增大，交错布孔筛管的极限弯矩一直大于其他2种布孔形式，而螺旋布孔筛管的极限弯矩最小。在此参数范围内筛管的布孔形式建议采用交错布孔形式。

2.3 孔径和孔密对筛管极限弯矩的影响

径厚比取16.89，建立3种布孔形式下不同孔径和孔密下筛管的有限元模型，分析孔密和孔径对筛管极限弯矩的影响规律，结果如图6所示。由图6可知，相同布孔形式下，筛管的极限弯矩随着孔径的增大而减小。随着孔径的增大，不同布孔形式筛管的极限弯矩近似呈直线下降。不同孔密下，筛管布孔形式对筛管的极限弯矩影响程度不同，在研究范围内分为3个区域，具体如下：在①区域内，不同布孔形式的筛管极限弯矩近似相等；在②区域，交错布孔筛管的极限弯矩最大；在③区域，随着孔径的增大，交错布孔筛管极限弯矩降低速度最快，其他2种布孔形式筛管极限弯矩的降低速度相近；在此区间内螺旋布孔筛管的极限弯矩最大而交错布孔筛管的极限弯矩最小。

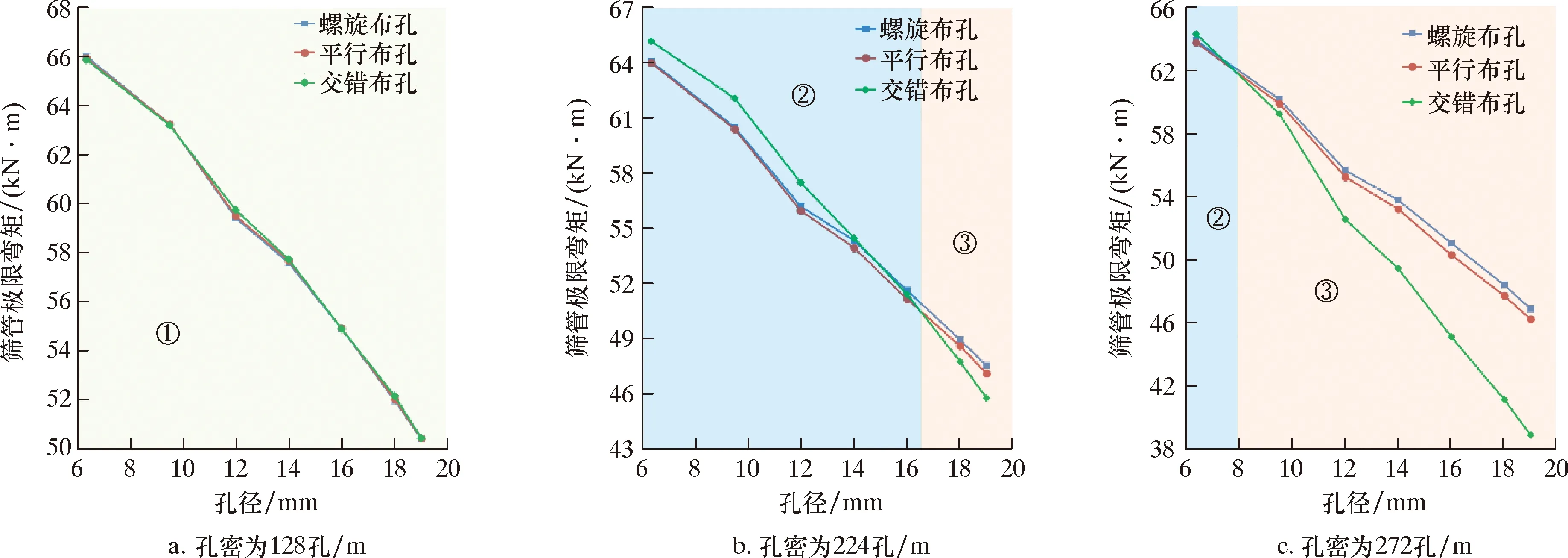
图6 孔径和孔密对筛管极限弯矩的影响Fig.6 Effect of hole size and density on ultimate bending moment of screen pipe

对比图6a、图6b和图6c可以发现，随着孔密的不断增大，筛管极限弯矩逐渐减小，且①、②区域逐渐消失，表明在孔密和孔径较大的参数下，筛管的布孔形式推荐采用螺旋布孔，以增强筛管的使用性能。

3 结论和建议

在不同的布孔参数范围内，不同布孔形式筛管的极限弯矩差异较大。根据经验来选择筛管的布孔形式和布孔参数容易导致筛管发生强度破坏或设计强度远大于实际工程要求的问题，造成筛管强度设计不足或者过于保守等问题。本文的研究成果可以针对不同的载荷工况要求优选筛管的布孔参数和布孔形式，在保证筛管强度的同时兼顾筛管制造成本，为现场筛管参数的选择提供了参考。主要研究结论如下：

(1)当孔密较小时，随着孔密和孔径的增大，3种布孔形式筛管的极限弯矩近似相等；当孔密在较大范围内时，随孔径和孔密的增大，交错布孔筛管极限弯矩最大；当孔密极大时，随孔径和孔密的增大，螺旋布孔筛管的极限弯矩最大，而交错布孔筛管的极限弯矩最小。在孔径和孔密较大时筛管推荐采用螺旋布孔形式。

(2)孔密在较小范围时，随着孔密和孔径的增大，3种布孔形式筛管的极限弯矩的降低速度相似；在孔密较大范围时，随着孔密和孔径的增大，交错布孔筛管的极限弯矩急剧降低而螺旋和平行筛管降低速度相近。

(3)综上所述，在不同的布孔参数和筛管参数范围内，弯曲载荷作用下筛管的最优布孔方式不同，建议根据具体的工况，利用建立的筛管极限弯矩计算模型对筛管的布孔形式进行优选。