基于虚拟样本优化选择的城市固废焚烧过程二噁英排放浓度预测

汤 健， 王丹丹， 郭子豪， 乔俊飞

(1.北京工业大学信息学部， 北京 100124； 2.计算智能与智能系统北京市重点实验室， 北京 100124；3.北京轨道交通技术装备集团， 北京 100070)

城市固废焚烧(municipal solid waste incineration, MSWI)技术是目前应用最为广泛的生活垃圾减容、减量和资源化处理手段[1-2]. 中国作为发展中国家，当前紧要的问题是控制MSWI过程的污染物排放[3-4]，尤其是降低被称为目前世界上最强毒性污染物——二噁英(dioxins, DXN)[5]的排放. 该污染物是造成MSWI电厂存在“邻避效应”的主要原因之一. 通过优化运行参数实现DXN排放最小化控制的前提是实现其排放浓度的在线实时预测[6].

目前，DXN排放浓度检测均针对MSWI过程末端的烟囱所排放的烟气G3进行[7-8]. 常用检测手段有：1) 基于高分辨气相色谱- 高分辨率质谱联机的离线直接检测法[9-10]，该方法需实验室化验分析，滞后时间尺度大(以周计)，受DXN高检测费用的制约，企业多以月/季或按需以不确定周期进行检测； 2) 在线间接检测法[11]，通过检测作为指示物/关联物的高浓度化学物质(如单氯苯等)和其与DXN间的映射模型实现，该方法滞后时间尺度居中(以h计)，但受限于检测设备复杂且价格昂贵、映射模型依赖DXN离线直接检测法等缺点，使其难以应用与推广； 3) 软测量法，构建以相关易检测过程变量和常规污染物浓度为输入的数据驱动模型，可实现DXN排放浓度的在线实时检测. 显然，上述前2种方法都难以支撑以限制DXN排放浓度为目标的MSWI过程实时运行优化控制. 此外，受限于DXN排放浓度检测的高难度、长周期、高费用等特性，以及MSWI过程的复杂性、动态性和不确定性，构建数据驱动预测模型所需的有标记真实样本(真输入- 真输出)十分稀缺.

数据驱动建模常用于数据足够丰富且样本真值获取成本相对较低的场景[12]. 本文所研究的MSWI过程DXN排放浓度预测问题可归类为典型的“小样本问题”. 通常，研究学者将样本数量小于30的建模问题称为“小样本问题”[13-14]. 显然，小样本集难以反映真实的工艺流程特性，这导致有效的预测模型难以建立. 除此之外，工业过程数据多具有较强非线性，也存在噪声、缺失值和不确定性等问题，这使得基于小样本构建数据驱动模型难以提取有效知识[15]. 因此，需要考虑如何克服上述数据特性以构建模型. 小样本问题的本质是因样本数量有限导致其分布稀疏而不能完全表征真实数据分布. 此外，样本间的信息间隔较大也进一步恶化了建模样本对总体数据空间的表征能力；小样本数据通常还存在分布不平衡等问题，即样本较为集中地分布在某些区域，这导致模型训练存在偏差. 因此，基于小样本构建的模型往往具有片面性和偏差性，其预测结果并不能真实反映实际输出. 目前，已有多种机器学习方法用于小样本数据建模，包括基于灰度[16]、基于支持向量机[17]、基于核回归[18]和贝叶斯网络等. 但是，在样本数量不足、分布稀疏、分布不平衡的情况下，上述算法均会出现“过拟合”现象，模型的泛化性能差、鲁棒性弱.

解决上述问题的手段之一是通过撷取小样本数据间隙中存在的潜在信息产生适当数量虚拟样本，即虚拟样本生成(virtual sample generation, VSG)，进而提高训练样本对总体数据特征的表征能力和模型的学习与泛化能力. 虚拟样本思想最初由模式识别领域的科学家Poggio等[19]提出. 之后，研究者相继提出了扩散神经网络(diffusion neural network, DNN)、整体趋势扩散技术(mega-trend-difusion, MTD)、基于高斯分布和Monte Carlo算法[20]等多种VSG技术，在柔性制造系统调度、癌症识别、可靠性分析等诸多领域得到了广泛的应用[21].

但是，目前上述研究中的VSG多面向分类问题，本文主要关注如何利用VSG辅助构建MSWI过程DXN排放浓度模型，即面向回归问题的VSG. 文献[13]给出了真实样本与虚拟样本分布间的关系，表明了VSG的本质是通过“填充”期望样本空间分布中的不完整和不平衡信息以实现样本扩充. 进一步，文献[22]证明VSG技术等价于将先验知识合并为正则化矩阵. 为实现样本扩充，文献[23]提出噪声注入的非线性VSG方法；文献[24-25]提出基于遗传算法和粒子群优化(particle swarm optimization, PSO)生成虚拟样本的VSG策略，有效地提高了建模精度；文献[26]提出了产生通用结构数据的VSG策略. 为去除真实样本中的噪声信息，文献[27-28]提出了基于神经网络隐含层映射的VSG技术. 最近，文献[29]提出基于改进大趋势扩散和隐含层插值的VSG方法，并将其应用于MWSI过程DXN排放浓度预测. 以上方法存在的共性问题是所生成的虚拟样本之间存在冗余，即存在不利于预测模型泛化性能的“坏”虚拟样本. 如何去除虚拟样本间的冗余仍是有待解决的开放性问题.

综上，本文提出基于虚拟样本优化选择的DXN排放浓度预测策略以及基于PSO和等间隔插值VSG的DXN排放浓度预测模型构建方法. 首先，依据已有研究获取的输入特征，基于改进MTD技术对约简小样本的输入/输出进行域扩展；然后，结合机理知识采用等间隔插值方式生成虚拟样本输入，再采用映射模型获得虚拟样本输出，并结合扩展输入/输出边界对虚拟样本进行删减以获得候选虚拟样本；接着，基于PSO算法对候选虚拟样本进行优化选择；最后，基于优选虚拟样本与约简小样本组成的混合样本构建预测模型. 结合某焚烧厂的多年DXN数据验证了上述方法的有效性.

1 MSWI过程描述与DXN建模策略

城市固废通常由市政运输车收集和称重后倾倒至密封的固废池内，经一周左右的堆酵后通过抓斗将其倒至焚烧炉料斗内，再由给料器推送至炉排；在焚烧炉内依次经历干燥、点燃、燃烧和燃烬4个阶段，其中：残渣掉入水冷渣斗后由捞渣机将其推入渣坑内，收集后送至填埋场处理；由一燃室、二燃室产生的高温烟气对余热锅炉加热产生高压蒸汽并推动汽轮发电机产生电力；锅炉出口烟气G1、消石灰和活性炭进入反应器，其产生的飞灰进入飞灰罐，烟气进入袋式除尘器后被除去烟气颗粒物、中和反应物和活性炭吸附物，经处理后分为3个部分，其中：尾部飞灰进入飞灰罐，部分烟灰混合物在混合器中加水后重新进入反应器，尾部烟气即烟气G2由引风机经烟囱排入大气即烟气G3，G3中含有HCL、SO2、NOx、HF和DXN等污染气体. 国内某厂的炉排炉焚烧工艺流程如图1的下半部分所示.

由图1可知，MSWI过程所产生的DXN分别包含在焚烧灰、飞灰和烟气3种产物中，其中烟气按照排放阶段分为：DXN产生时的烟气G1、DXN被吸附后的烟气G2和包含DXN排放至大气的烟气G3. 机理上，DXN的产生来源包括固废不完全燃烧和新规合成反应生成2类[30]. 通常，为保证DXN等有毒有机物的有效分解，在固废焚烧阶段的烟气温度应达到至少850 ℃并保持2 s. 为减低排放烟气中的DXN浓度，在烟气处理阶段需要向反应器内喷射消石灰和活性炭以吸附DXN以及某些重金属. 此外，余热锅炉和烟气处理阶段的积灰所固有的DXN记忆效应也会导致DXN排放浓度增加. 上述不同阶段的过程变量均以s为周期由现场分布式控制系统DCS进行采集和存储. 此外，烟气G3中的易检测气体(CO、HCL、SO2、NOx和HF等)浓度能够通过CEMS系统进行实时检测，并且与DXN浓度存在相关性. 但是，焚烧企业或环保部门通常以月/季或按需以更长不确定周期采用离线直接检测法对排放烟气G3中的DXN浓度进行检测.

综上可知，烟气G3中的DXN浓度与MSWI过程中不同阶段的过程变量相关，并且构建DXN预测模型的数据(真输入- 真输出)具有样本数量稀缺、分布不均衡和输入特征维度高等特性. 因此，本文提出了基于虚拟样本优化选择的DXN排放浓度预测策略，如图1上部所示. 该策略由输入数据预处理与特征选择、样本输入/输出区域扩展、候选虚拟样本生成、虚拟样本优化选择、基于混合样本的预测模型构建共5个模块组成，其功能如下.

1) 输入数据预处理与特征选择模块：对过程变量、易检测气体浓度和DXN排放浓度数据进行剔除离群点、匹配输入/输出数据对等处理以获取高维输入/单输出的原始小样本，同时结合MSWI过程不同阶段特性和机理知识进行特征选择进而获得约简小样本.

2) 样本输入/输出区域扩展模块：基于领域专家知识和相关技术对约简小样本建模数据集的输入/输出域进行扩展，获得期望建模样本输入/输出的可行域上下限.

3) 候选虚拟样本生成模块：基于约简小样本输入特征，在虚拟样本可行域中进行等间隔插值以生成临时虚拟样本输入，通过采用约简小样本构建的映射模型获得临时虚拟样本输出，因在可行域外存在部分临时虚拟样本，故对其进行删减以获得候选虚拟样本.

4) 虚拟样本优化选择模块：因候选虚拟样本中仍可能存在不符合真实数据特征的样本，基于智能优化算法对候选虚拟样本进行优选以获得最优虚拟样本子集.

5) 基于混合样本的预测模型构建模块：基于混合样本构建DXN排放浓度预测模型.

2 建模方法及算法实现

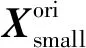
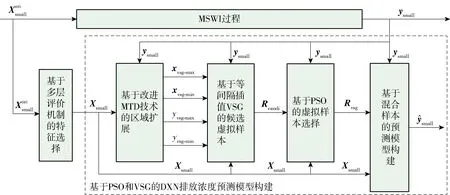
图2 基于PSO和VSG的DXN排放浓度预测模型构建方法Fig.2 DXN emission concentration prediction model based on PSO and VSG

2.1 基于改进MTD技术的区域扩展模块[29]

1) 样本输入的区域扩展

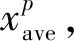
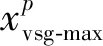
(1)

(2)

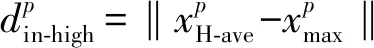
(3)

(4)

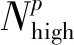
2) 样本输出的区域扩展

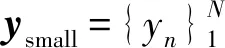
(5)

(6)

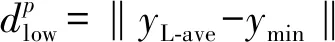
2.2 基于等间隔插值VSG的候选虚拟样本模块

首先，针对约简小样本数据，选择2组相邻样本进行等间隔插值以生成虚拟样本输入. 假定对每组相邻样本以相等间隔生成Nequal组数据，以第n和第(n+1)样本中的第p个特征为例，具体实现为

(7)

(8)

式(7)(8)是针对原始小样本空间的等间隔插值，类似地，结合虚拟样本域扩展上下限，分别对下扩展域空间和上扩展域空间进行等间隔插值以得到全部虚拟样本输入.

接着，基于约简小样本，构建随机权神经网络(random weight neural networks, RWNN)函数，并将其作为映射模型获得虚拟样本输出，有

equal=Γmap(ωequal,bequal,Xequal)βequal=Hequalβequal

(9)

式中：Γmap(·)为映射函数；ωequal和bequal分别为基于RWNN映射模型的输入层到隐含层的权值和偏置；βequal为相应的输出权值；Hequal为其隐含层矩阵.

由以上描述，获得未删减的等间隔插值虚拟样本Requal={Xequal,equal}. 然后，根据虚拟样本输出的上/下限yvsg-max/yvsg-min以及约简小样本的上/下限ymax/ymin，对不同区域虚拟样本进行删减. 可获得候选虚拟样本Rcandi={Xcandi,candi}，式中，Xcandi和candi分别表示候选虚拟样本输入和输出，且Rcandi∈RNcandi×P，Ncandi为候选虚拟样本数量.

2.3 基于PSO的虚拟样本选择模块

PSO是模拟鸟群在飞行过程中始终保持队形且不会相撞的生物行为的智能优化算法. 粒子群中任何粒子都有自己的位置与速度，在迭代过程中不断地更新自己的位置以在可行域内寻找到目标函数最优解. 本文中，基于PSO进行虚拟样本选择的基本原理类似于基于PSO的特征选择方法[32]，即期望粒子群在迭代过程中寻找最优虚拟样本子集以使得模型泛化性能最佳，将虚拟样本的选择问题转化为基于模型的优化问题. 具体地，在建模过程中，控制RWNN模型结构和模型输入特征数量不变，再对影响模型性能的建模样本作为变量(建模样本包含约简小样本训练集和粒子选择的部分虚拟样本)进行选择. 那么，在对模型泛化性能进行优化时，即对建模样本中所包含的虚拟样本进行了优化选择.

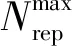
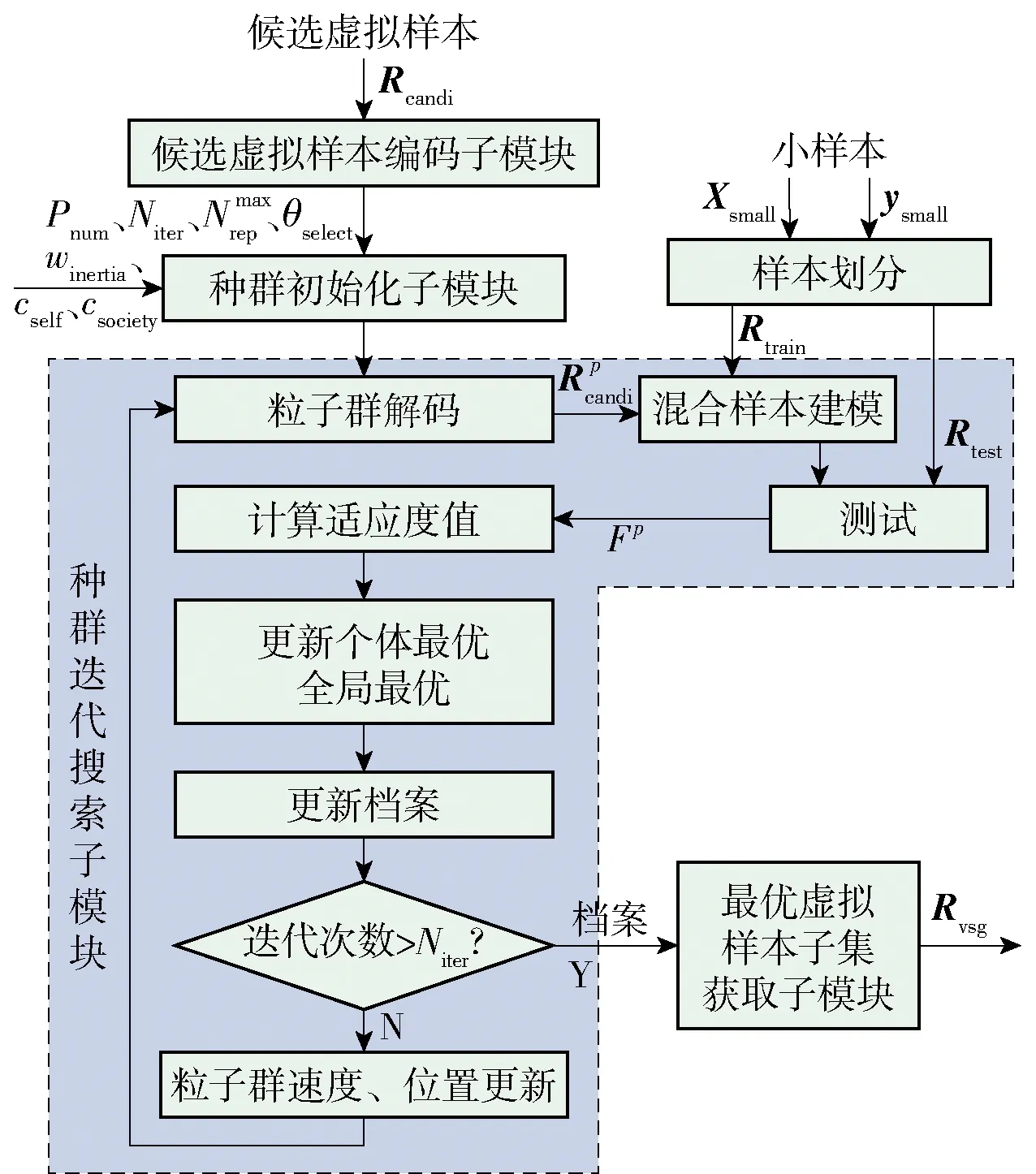
图3 基于PSO的虚拟样本选择流程Fig.3 Virtual sample selection flow based on PSO

虚拟样本的选择流程是：首先，在采用PSO算法对候选虚拟样本进行优化选择前对其进行编码，即对粒子进行设计；接着，对PSO算法进行初始化，即初始化粒子群的位置和速度等相关参数；然后，在粒子群迭代搜索过程中进行寻优，直到达到迭代次数；最后，对档案中的粒子进行解码以获得最优虚拟样本子集Rvsg.

2.3.1 候选虚拟样本编码子模块

利用PSO算法进行虚拟样本选择的问题可抽象为简要范式，即

minf(z) s.t.z∈Ω

(10)

式中：z=(z1,z2，…,zn)为决策变量，即自变量；Ω为可行搜索域，表示决策变量可到达的空间范围；f(z):Ω→S为优化目标函数，S是目标空间.

利用PSO算法进行虚拟样本选择的目的是寻找最优的虚拟样本子集以获得最优的模型泛化性能. 此处将DXN排放浓度预测模型的测试性能指标作为优化目标. 对决策变量进行抽象，有

(11)

式中：Ncandi为候选虚拟样本集Rcandi中虚拟样本的数量，相应地虚拟样本的编码为(1,2，…,n,…,Ncandi). 决策向量z包含的Ncandi个决策变量与候选虚拟样本一一对应，即粒子的每维均对应一个虚拟样本.

显然，每个决策变量都在(0,1)中取值，即决策向量的可行域为Ω={(0,1)Ncandi}R. 由此可知，第p个粒子的解码方法可描述为

(12)

式中θselect为虚拟样本的选择阈值.

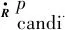
2.3.2 种群初始化子模块

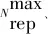
(13)

接着，定义粒子适应度值、个体最优位置、全局最优位置、档案等变量，以便在种群迭代搜索中作为关键因素不断更新.

2.3.3 种群迭代搜索子模块

种群在不断迭代更新过程中对可行域空间进行启发式搜索，个体和全局最优位置指导其下一步的搜索方向和步长，进而不断靠近最优位置，并将最优解存入档案中. 评价粒子位置优劣的标准是目标函数f(z)的值，即粒子的适应度值.

种群迭代搜索的主要步骤包括：适应度值计算、个体最优和全局最优更新、档案更新、粒子群速度和位置更新，最终获得最优虚拟样本子集.

1) 适应度值计算

基于PSO对虚拟样本进行选择的优化目标为

minf(z)=fFitness(z,Xsmall,ysmall)

(14)

式中fFitness(·)为计算粒子适应度值的映射函数，以种群中第p个粒子为例描述其映射过程，有

(15)

式中：fRWNN(·)表示基于临时混合样本集R′mixp构建的RWNN映射模型；Fp为基于测试集Rtest获得的测试性能指标，即适应度值.fdecode(·)、fdivision(·)和ftrain(·)分别为解码函数、样本划分函数和模型训练函数，描述为

(16)

{Rtrain,Rtest}←fdivision(Xsmall,ysmall)

(17)

fRWNN(·)←ftrain(R′mixp)

(18)

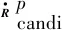
(19)

2) 个体和全局最优更新

种群的个体最优和全局最优共同启发粒子的搜索方向和步长，其更新方法为

(20)

(21)

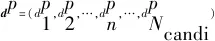
3) 档案更新

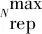
档案更新策略为

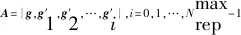
(22)

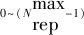
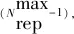
4) 粒子群速度和位置更新

种群在可行域内的搜索方向和步长取决于粒子速度，后者受该粒子当前位置、个体及全体最优位置的影响. 粒子群迭代中通过跟随当前最优位置的引导得到最优解.

粒子更新其速度与位置，有

(23)

(24)

式中：winertia为惯性权重，表示搜索步长，随迭代次数线性减小；r1和r2均服从[0, 1]间的均匀分布；cself和csociety为学习因子，分别代表粒子搜索方向受个体和全局最优位置的影响程度，体现粒子的个性和社会性的统一.

5) 最优虚拟样本子集获取子模块

依据以上步骤，种群不断进行迭代搜索，直至迭代次数大于设定值Niter，则停止寻优；对档案中最优解和次优解多次计算适应度值求平均，以此作为指标重新选择最优解；对最优解进行解码后获得最优虚拟样本子集Rvsg.

2.4 基于混合样本的预测模型构建模块

将最优虚拟样本子集与约简小样本训练集组合形成混合样本集

Rmix={Rtrain,Rvsg}

(25)

首先，计算隐含层神经元的输出矩阵Hori，且

(26)

式中：hml=Γmap(ωl,bl,xm)为隐含层节点值；ω={ω1,ω2,…,ωl,…,ωL}为随机生成的输入层和隐含层神经元之间的权值；b={b1,b2,…,bl,…,bL}为神经元偏置；L为隐含层节点数量；Xmix为混合样本集的输入；M为混合样本集样本数量；Γmap表示以sigmoid为激活函数的映射函数.

然后，利用广义逆矩阵计算隐含层与输出层之间的权值β，且

β=(Hori)+ymix

(27)

式中：(Hori)+为Hori的广义逆；ymix为混合样本集的输出.

在基于RWNN预测模型的构建步骤中模型隐含层节点数采用遍历法确定.

RWNN模型基于混合样本集的预测输出为

mix=Horiβ

(28)

接着，使用测试集Rtest进行测试，

test=Γmap(ω,b,Xtest)β=Htestβ

(29)

式中：Xtest为测试样本集的输入；Htest为测试集在模型上的隐含层输出；test为测试集的预测输出.

3 实验验证

采用DXN数据验证所提方法,设计3组对比实验分别使用不同训练集构建DXN排放浓度预测模型:实验A基于约简小样本训练集;实验B基于MTD扩展的等间隔插值法获得的混合样本;实验C基于MTD扩展的等间隔插值和PSO选择后的混合样本.

为降低随机性对实验效果的影响，实验均重复执行30次. 上述方法中，等间隔插值法的扩展倍数采用遍历法确定.

3.1 数据集描述

本文所采用DXN数据源于北京某基于炉排炉的MSWI焚烧企业，涵盖了2012—2018年所记录的有效DXN排放浓度检测样本34个；原始变量314维经预处理后为287维. 本文实际采用的DXN排放浓度简约样本是文献[31]进行特征选择后的数据集，共34个样本，输入特征18维，输出1维，即DXN排放浓度.

3.2 实验结果

3.2.1 基于改进MTD的域扩展结果

分别采用一般MTD与改进的MTD域扩展方法对可行域空间进行扩展，18维输入特征的最大值xmax和最小值xmin经过域扩展得到虚拟样本的可行域上限xvsg-max、下限xvsg-min和空间扩展率sx，如图4所示.

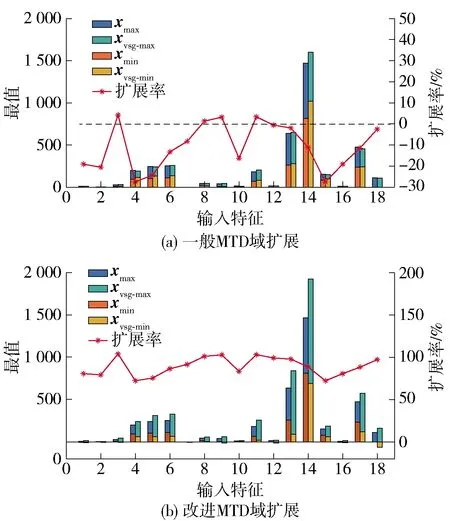
图4 DXN数据输入特征域扩展前后比对及其域扩展率Fig.4 Comparison of DXN data input features before and after domain extension, and their domains extension rate

输出的最大值ymax和最小值ymin经过域扩展得到输出可行域上限yvsg-max、下限yvsg-min和扩展率sy如表1所示.

表1 DXN数据输出域扩展前后对比

如图4和表1所示，一般MTD方法对输入特征的平均扩展率为-10.60%，对输出的扩展率为1.98%. 而改进MTD方法对虚拟样本输入特征的可行域整体空间得到了有效扩展，且扩展率平均约为89.40%. 考虑样本输出的物理意义，将域扩展的最小值限制为0，其可行域整体扩展率为64.20%.

3.2.2 基于等间隔插值的VSG结果

依据虚拟样本的域扩展结果和映射模型，进行等间隔插值生成虚拟样本. 虚拟样本输出及前5个输入特征如表2所示(以插值倍数3、样本6和样本7间插值为例).

表2中，输入1～5分别表示反应器入口氧气浓度、燃烧炉排右空气流量、二次空预器出口温度、干燥炉排入口空气温度、燃烧炉排2-2左内温度，输出

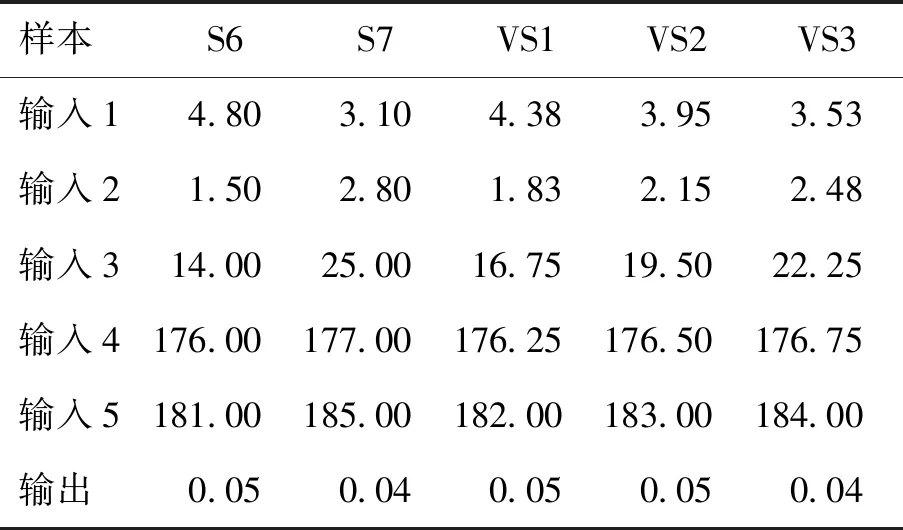
表2 DXN数据等间隔插值生成虚拟样本输入和输出

为DXN排放浓度.

基于等间隔插值生成的虚拟样本删减后剩余的数量如图5所示. 基于等间隔插值生成的虚拟样本平均删减率为41.997%，虚拟样本“合格率”较低的原因可能是：基于改进MTD域扩展范围与实际特征空间存在差异，构建的映射模型存在随机性.

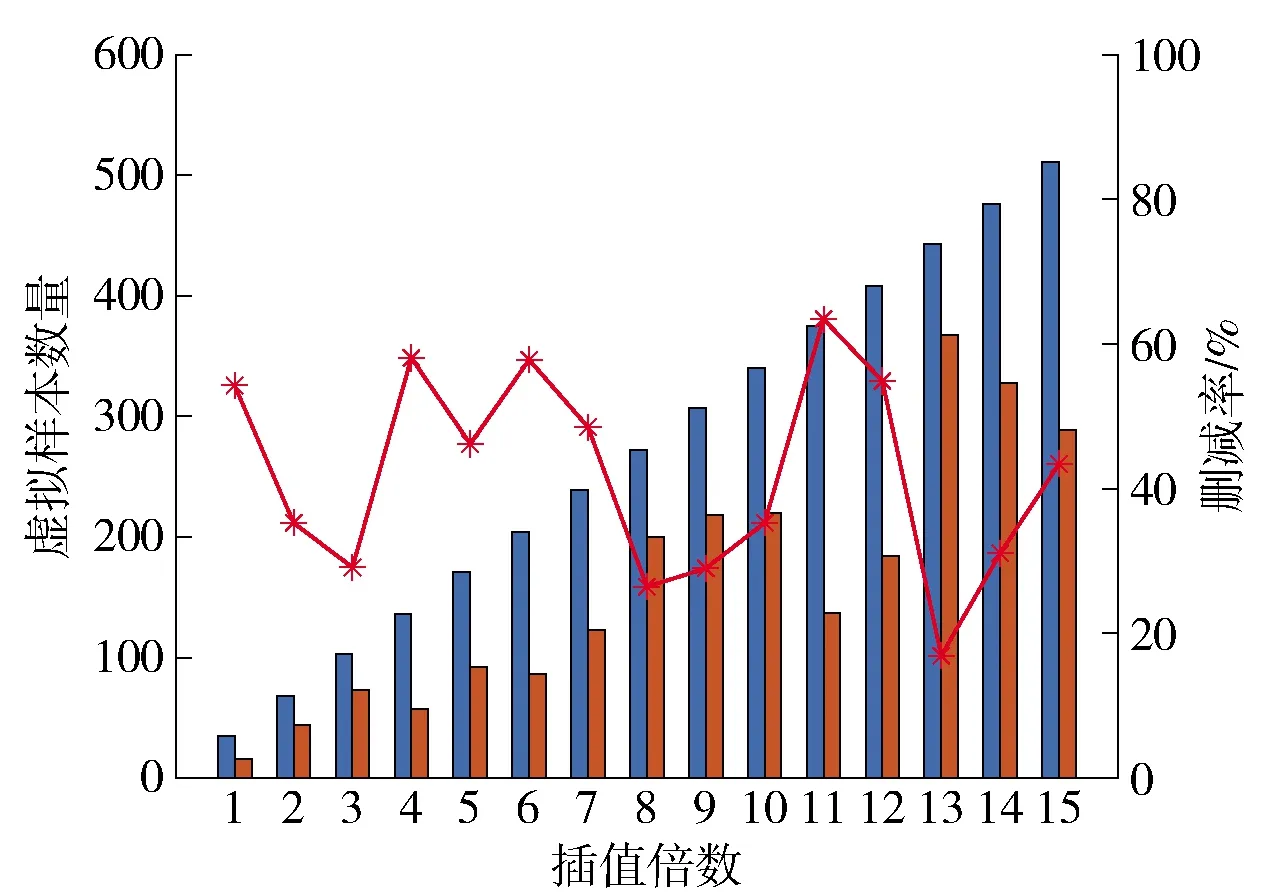
图5 DXN数据生成虚拟样本删减前后数量对比Fig.5 Comparison of the number of virtual samples generated from DXN data before and after deletion

3.2.3 基于PSO虚拟样本选择后的结果

进行PSO样本选择算法的相关参数设定如表3所示.

表3 DXN数据PSO样本选择算法参数设定

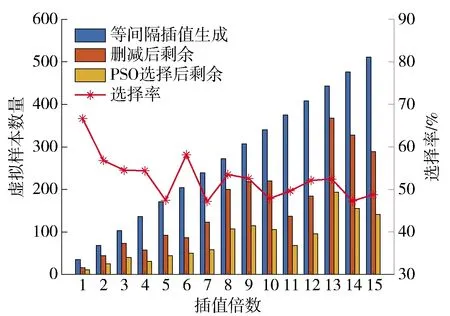
图6 DXN数据经PSO样本选择前后虚拟样本数量对比Fig.6 Comparison of the number of virtual samples before and after PSO selection for DXN data

经PSO选择前后的虚拟样本数量对比如图6所示. PSO优选算法对候选虚拟样本的平均选择率为52.619%，最终剩余虚拟样本82.5个，其样本扩展率为585.30%.

以插值倍数14为例，获得最终虚拟样本的结果(随机选择4个虚拟样本的前5个输入特征)如表4所示.

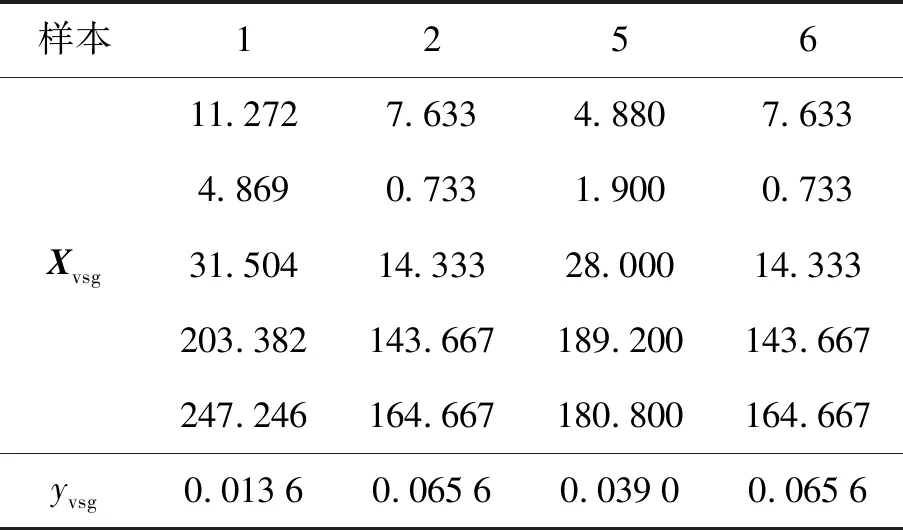
表4 DXN数据经PSO选择后虚拟样本输入和输出

为了对比DXN数据的约简小样本、候选虚拟样本、PSO选择后虚拟样本和混合样本的分布情况，选择了样本的输出及其第3、6、7个输入特征进行分析，它们的概率分布柱状图如图7～10所示.

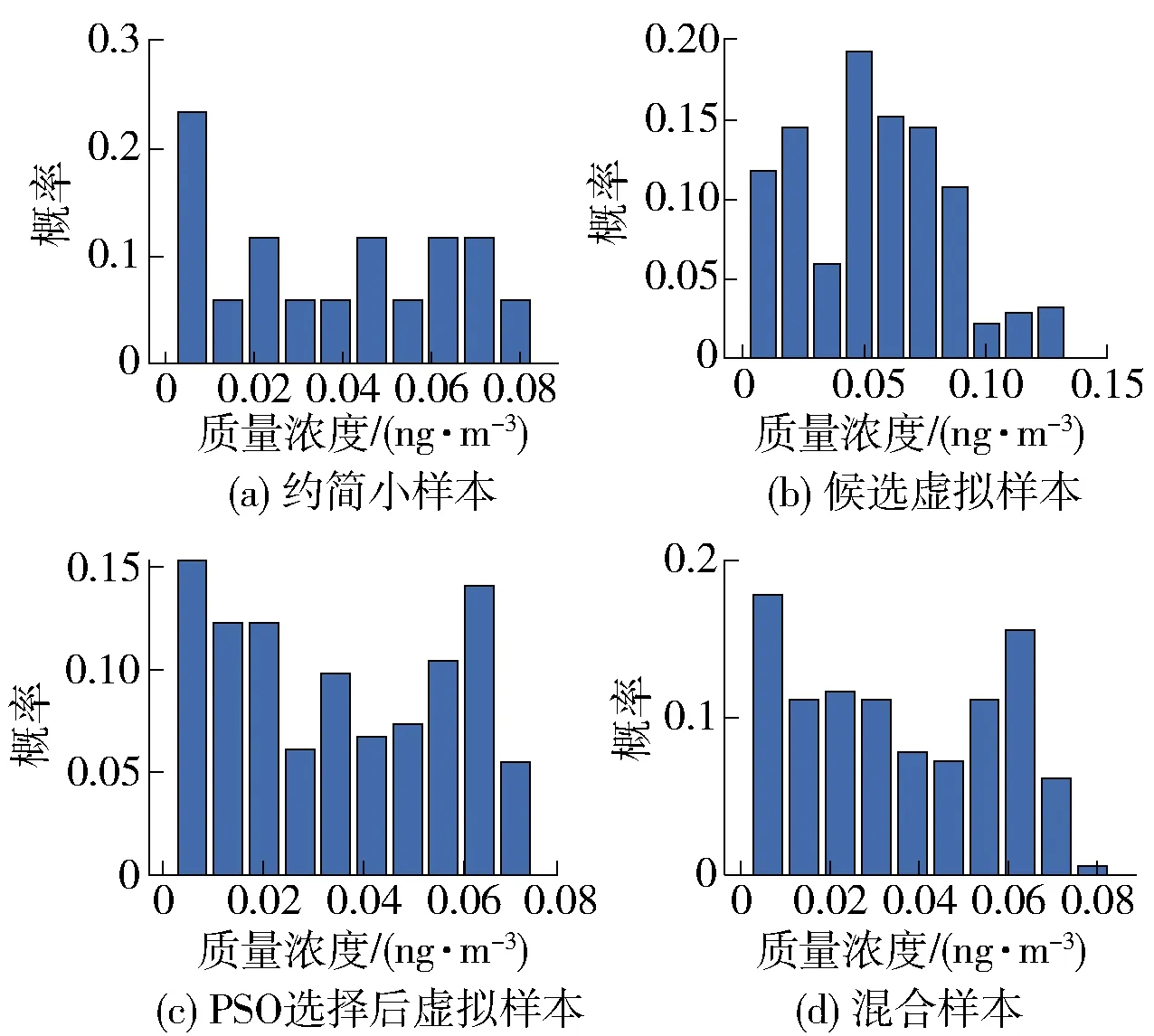
图7 不同样本集的输出分布情况对比Fig.7 Output distribution of different sample sets

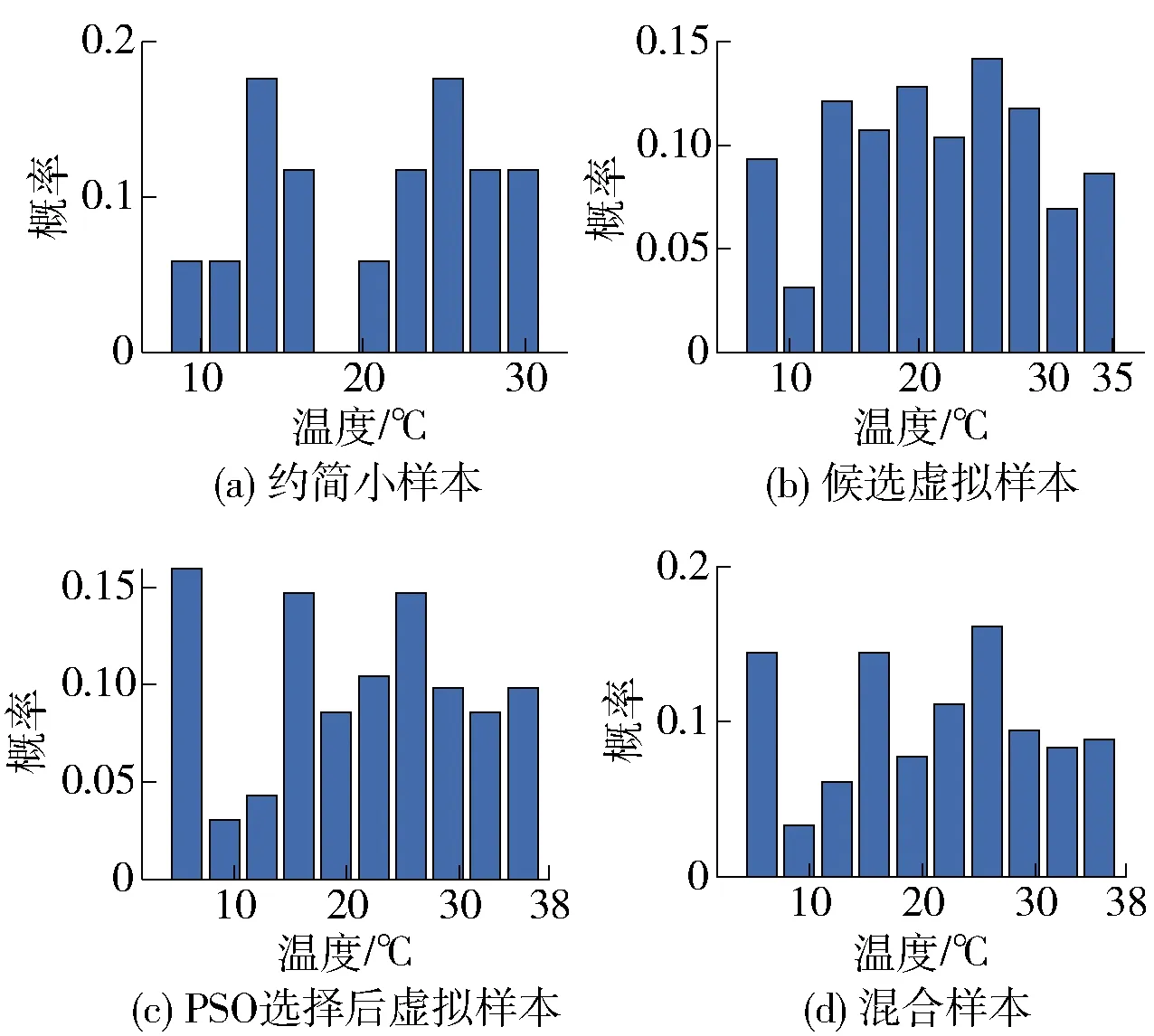
图8 不同样本集的第3输入特征分布情况Fig.8 Distribution of the 3rd input feature of different sample sets

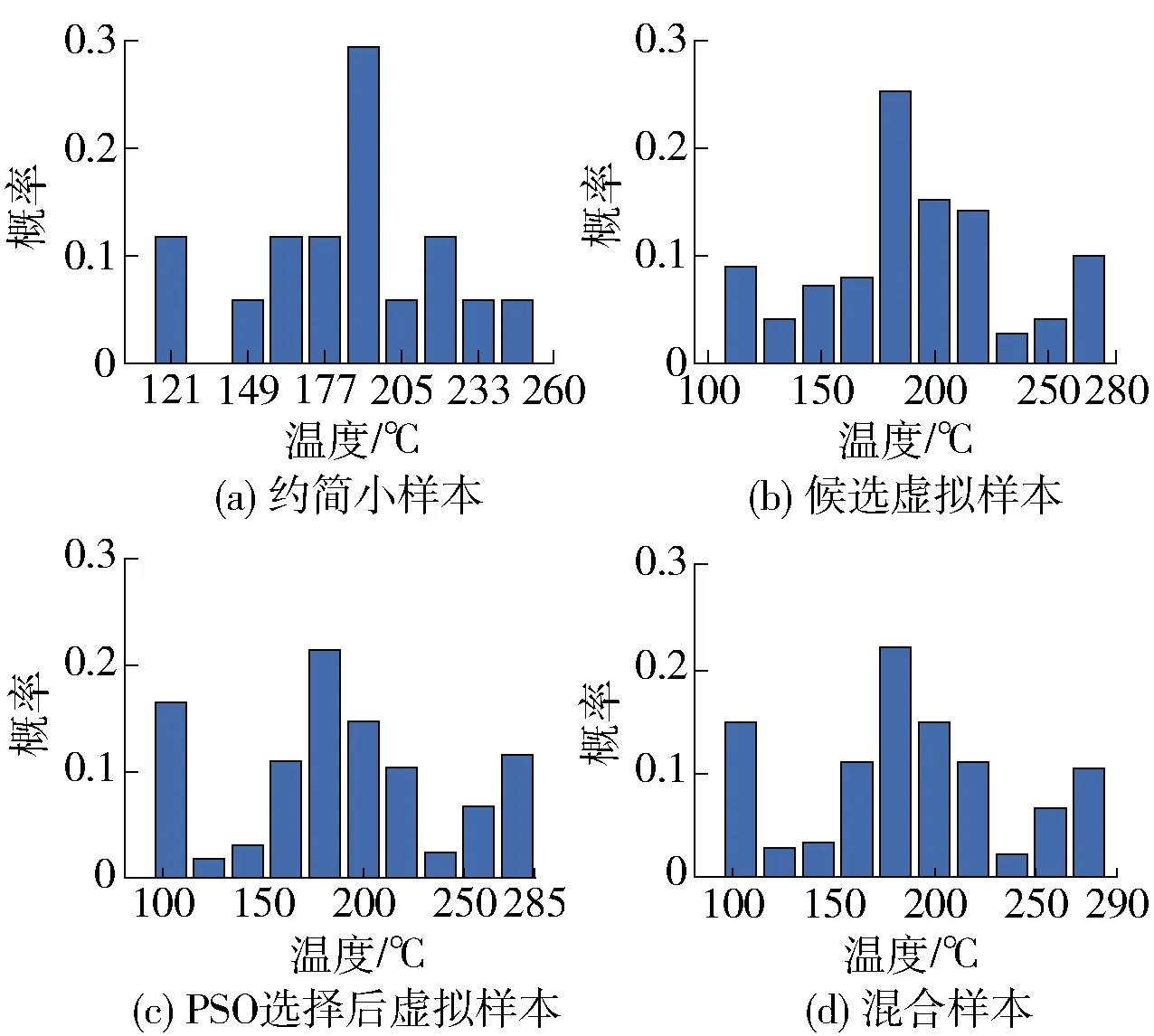
图9 不同样本集的第6输入特征分布情况Fig.9 Distribution of the 6th input feature of different sample sets

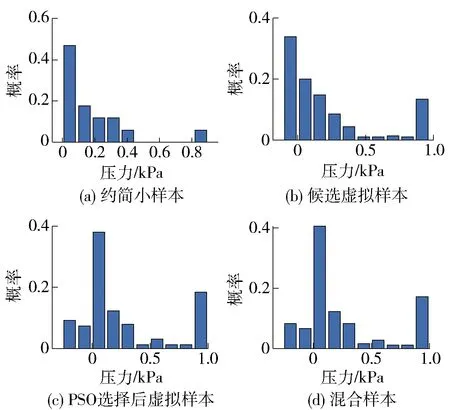
图10 不同样本集的第7输入特征分布情况Fig.10 Distribution of the 7th input feature of different sample sets

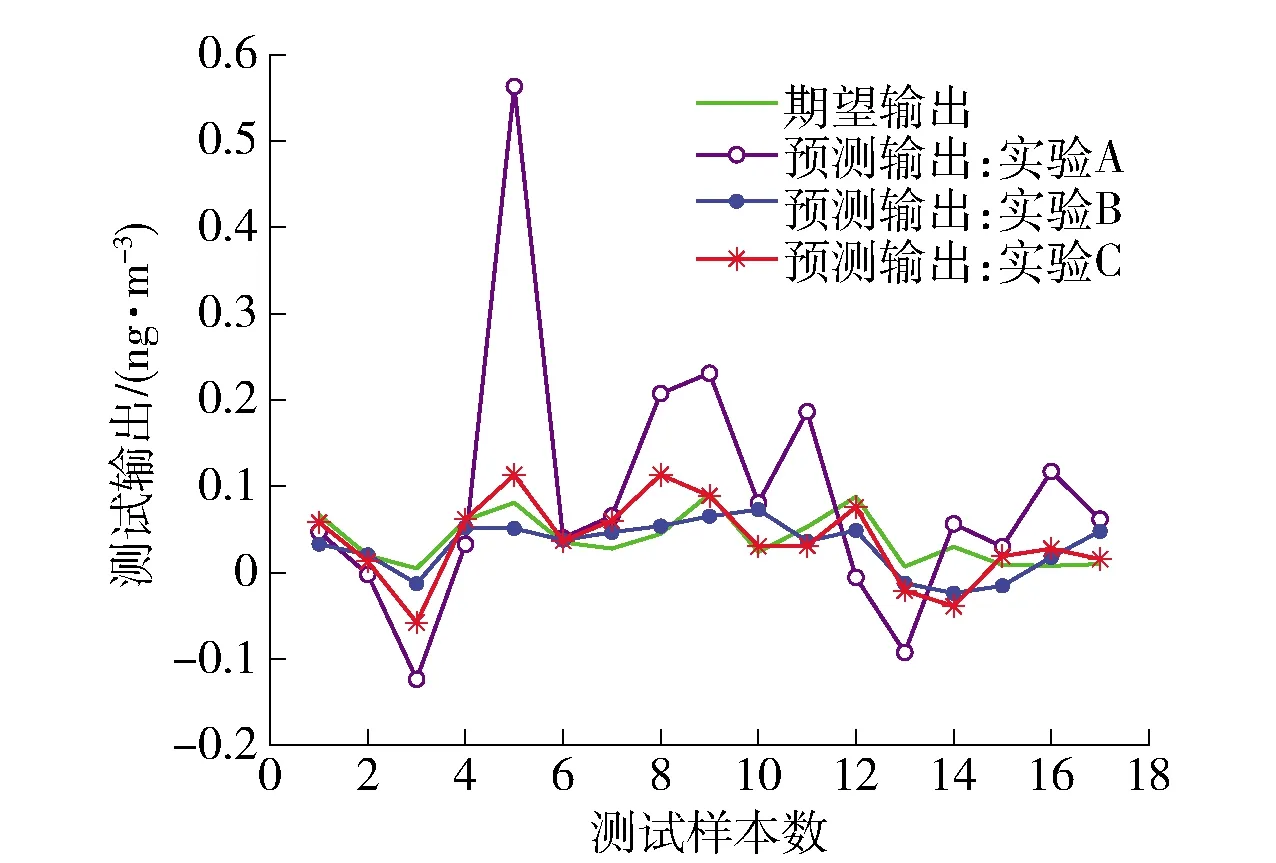
图11 DXN数据测试预测输出结果对比Fig.11 Comparison results of the testing predicted outputs for the DXN data

基于等间隔插值生成的虚拟样本有效扩充了虚拟样本的数量. 同时，如表4和图7～10所示，生成的虚拟样本经删减和PSO选择后，剩余的虚拟样本均能够对约简小样本间的信息间隙进行有效填充，尤其是有效地填补了实际特征空间的边缘区域，且能够保留约简小样本分布的主要特征.

3.2.4 基于混合样本的预测模型构建结果

图11为实验A、B、C所构建的模型测试输出对比图，展示了插值倍数为9时，模型测试的输出预测值.

本文所提方法构建的预测模型性能优于约简小样本构建的预测模型，其预测精度还有待提高.

3.3 对比讨论

表5为对比实验的测试结果. 对比表5的实验A、B和C可知：1) 约简小样本集(无VSG方法)的RMSE均值为0.078 8，本文所提方法后的平均RMSE为0.016 7. 结果表明，本文所提方法可整体提高小样本建模性能78.807%. 2) 对比实验B和C可知，经PSO选择后的虚拟样本在数量减少52.744%的情况下，混合样本建模测试的RMSE均值改善了16.583%. 因此，验证了本文所提基于PSO对虚拟样本进行筛选方法的有效性，也表明了合理虚拟样本数量的重要性，但如何生成更多有效的虚拟样本仍然有待深入；3) 本文所提方法RMSE方差较小，表明其稳定性较好. 对比文献[29]的实验结果，本文所提方法在最佳RMSE上具有优势，这是由于本文与文献[29]所构建模型的结构差异造成的.

由上述结果可知，所提方法基于DXN数据集能够对生成的冗余虚拟样本进行有效筛选，筛选后的虚拟样本扩展了约简小样本的数量，并能够有效填补约简小样本间的信息间隙，改善了虚拟样本的有效性、平衡性和数据完整性. 特别地，虚拟样本也能够有效填补实际特征空间边缘的信息间隙. 而所提方法构建的模型性能有待提高，所以如何生成更多、更优质的虚拟样本以进一步改善模型的预测性能是下一步有待解决的问题.

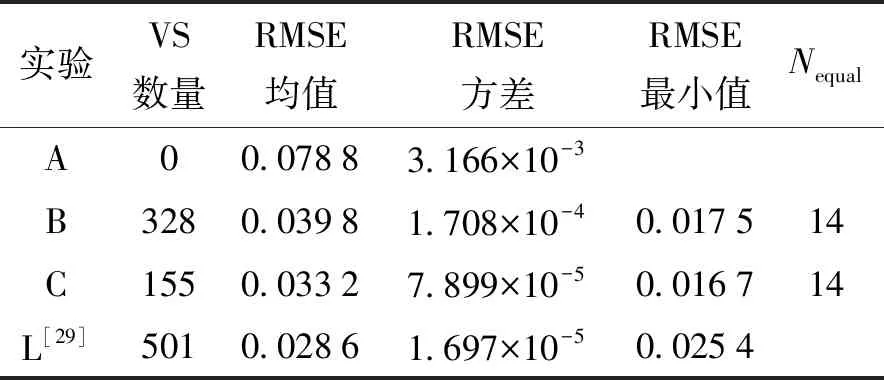
表5 DXN数据实验结果对比

4 结论

1) 基于改进的MTD域扩展和等间隔插值方法生成的候选虚拟样本能够有效地扩展样本数量，填补真实样本空间的信息空白.

2) 利用基于PSO的样本选择策略对候选虚拟样本进行筛选，能够有效地去除不良虚拟样本，优选的虚拟样本能够对约简小样本间的信息间隙和实际样本空间的边缘区域进行有效填充，并且保留了约简小样本分布的主要特征.

3) 基于工业实际DXN数据验证了所提策略和方法的有效性. 如何获取更多具有互补特性的虚拟样本，如何确定最佳虚拟样本数量以获得模型最佳预测性能是下一步的研究方向.